基于不完备背景的3类SE-ISI概念约简

朱朵朵,任睿思,赵思雨,魏 玲,3

(1.西北大学 数学学院,陕西 西安 710127;2.西北大学 概念、认知与智能研究中心,陕西 西安 710127;3.闽南师范大学 数学与统计学院,福建 漳州 363000)

形式概念分析(formal concept analysis, FCA)是德国数学家Wille[1]在1982年提出的以形式背景为基础进行数据分析和知识发现的有效数学工具。目前,该理论已在概念格的构造[2-4]、属性约简[5-7]、规则提取[8]以及与其他理论的结合[9-10]等方面取得诸多成果。

约简理论是形式概念分析的一个重要研究课题。属性约简用部分属性保持全部属性所具有的某种特性不变,从而消除冗余属性和数据,但这个过程会损失原始信息。为避免原始信息的损失,2018年,魏玲等受布尔因子分析中因子分解的启发,提出保持二元关系不变的概念约简[11-12]。概念约简不仅完整保留了形式背景中的原始信息,而且减少了概念数量,降低了用形式概念分析解决问题的复杂性。近期,王霞等基于概念可辨识矩阵给出了概念约简方法[13];谢小贤等借助矩阵运算给出了概念特征和生成概念约简的方法[14];Zhao等给出了一套基于代表概念矩阵获得概念协调集判定定理、概念约简及概念特征的理论方法[15];马文胜等基于同效关系给出了概念约简和概念特征的获取方法[16]。此外,智慧来等提出了形式背景下面向对象概念约简[17];李俊余等研究了保持三元背景中所有三元关系不变的三元概念约简[18]。

实际生活中,信息缺失无处不在,不完备背景[19]的存在比形式背景更为普遍。针对不完备背景,Li等定义了近似概念并构建了近似概念格[20];Yao基于区间集理论定义了SE-ISI概念、ISE-SI概念和ISE-ISI概念3种部分已知概念[21];Ren等在Yao的研究基础上充分讨论了部分已知概念格的结构和关系[22];Wang等研究了不完备背景上SE-ISI概念格的属性约简[23];Li等将三支决策引入不完备背景,研究了基于三支近似概念格的属性约简[10]。

不完备背景上有SE-ISI概念、ISE-SI概念和ISE-ISI概念3种部分已知概念,本文探讨不完备背景的SE-ISI概念约简,其他两种部分已知概念约简问题可以进行类似的研究。

本文首先从确定拥有角度、可能拥有角度与所有原始背景信息角度,提出保持正信息、保持广义正信息与保持关系不变的SE-ISI概念约简;其次,给出这3类SE-ISI概念约简的求解方法;最后,讨论SE-ISI概念在每类SE-ISI概念约简下的特征与联系。

1 预备知识

定义1[19]称四元组IK=(G,M,{+,?,-},J)为不完备形式背景。其中:G={g1,g2,…,gp}为对象集;M={m1,m2,…,mq}为属性集;J为G、M及{+,?,-}之间的三元关系,即J⊆G×M×{+,?,-}。(g,m,+)∈J表示对象g具有属性m;(g,m,?)∈J表示不确定对象g是否具有属性m;(g,m,-)∈J表示对象g不具有属性m。

为简单起见,本文把不完备形式背景统称为不完备背景。

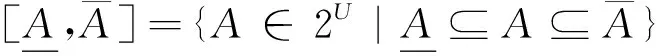
[B1,C1]∩[B2,C2]=[B1∩B2,C1∩C2],

[B1,C1]∪[B2,C2]=[B1∪B2,C1∪C2],

[B1,C1]-[B2,C2]=[B1-B2,C1-C2]。

(1)

(2)

(3)

(4)

(5)

(6)

例1表1为不完备背景IK=(G,M,{+,?,-},J)。其中:对象集G={1,2,3,4};属性集M={a,b,c,d,e,f,g}。若某对象具有某属性,则表中对象所在行与属性所在列的交叉位置记为+;若该对象不确定是否具有该属性,则相应位置记为?;若该对象不具有该属性,则相应位置记为-。IK对应的SE-ISI概念格L如图1所示,其中,ci(i=1,2,…,11)是相应SE-ISI概念编号。

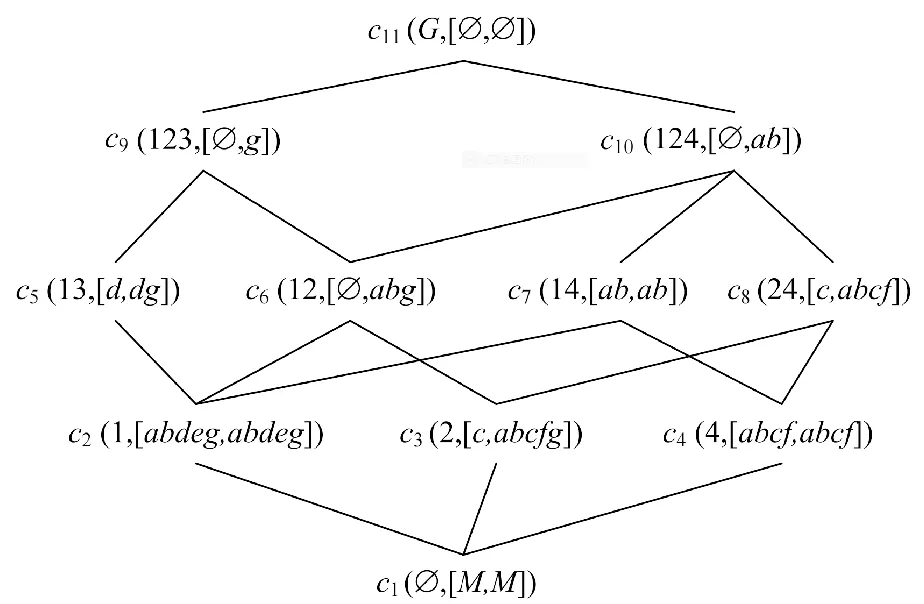
图1 SE-ISI概念格LFig.1 SE-ISI concept lattice L

表1 不完备背景IKTab.1 Incomplete context IK

2 3类SE-ISI概念约简

本节在不完备背景上分别定义保持正信息、广义正信息及关系不变的SE-ISI概念约简,并进一步讨论3者之间的关系。

2.1 3类SE-ISI概念约简的定义及存在性

首先给出保持正信息不变的SE-ISI概念约简。

与定义5类似,还可定义以下两种SE-ISI概念约简。

与前两种SE-ISI概念约简不同,保持关系不变的SE-ISI概念约简可用部分SE-ISI概念来保留不完备背景的全部信息。

不完备背景的关系取值只有+、-、?,若保持任意两种关系取值不变,则剩下一种也不变。后文通过保持取值为+和?的关系不变得到保持关系不变的SE-ISI概念约简。

定理1设IK为不完备背景,保持正信息不变的SE-ISI概念约简、保持广义正信息不变的SE-ISI概念约简以及保持关系不变的SE-ISI概念约简必存在。

类似地,可以证明保持广义正信息不变的SE-ISI概念约简和保持关系不变的SE-ISI概念约简必存在。

例2(续例1) 根据定义5、定义6及定义7可以验证SE-ISI概念集合F1={c2,c4,c5,c8},F2={c2,c5,c6,c8},F3={c2,c4,c5,c6,c8}分别是保持正信息、保持广义正信息及保持关系不变的SE-ISI概念约简。以F1为例,如果只需要例1不完备背景中确定拥有的信息,则不需要图1中所有SE-ISI概念,只需要F1中的4个SE-ISI概念即可。

2.2 3类SE-ISI概念约简之间的关系

根据2.1节给出的3类SE-ISI概念约简定义,本小节研究3类SE-ISI概念约简之间的关系。

定理2设IK为不完备背景,L为其SE-ISI概念格,有CCS=CCS+∩CCS+?。

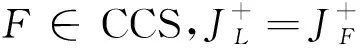
定理2表明保持关系不变的SE-ISI概念协调集一定是保持正信息和保持广义正信息不变的SE-ISI概念协调集。反之,如果一个集合同时是保持正信息和保持广义正信息不变的SE-ISI概念协调集,则其一定是保持关系不变的SE-ISI概念协调集。

推论1设IK为不完备背景,有CR⊆CCS+,CR⊆CCS+?。

证明因为CR⊆CCS,所以根据定理2可得:CR⊆CCS+,CR⊆CCS+?。

根据推论1,保持关系不变的SE-ISI概念约简一定是保持正信息和保持广义正信息不变的SE-ISI概念协调集。

定理3设IK为不完备背景,L为其SE-ISI概念格,有CR+∩CR+?⊆CR。

由定理3可知,如果一个集合同时是保持正信息和保持广义正信息不变的SE-ISI概念约简,则其一定是保持关系不变的SE-ISI概念约简。

基于上述分析,3类SE-ISI概念约简之间的关系如图2所示。其中,∧表示合取。

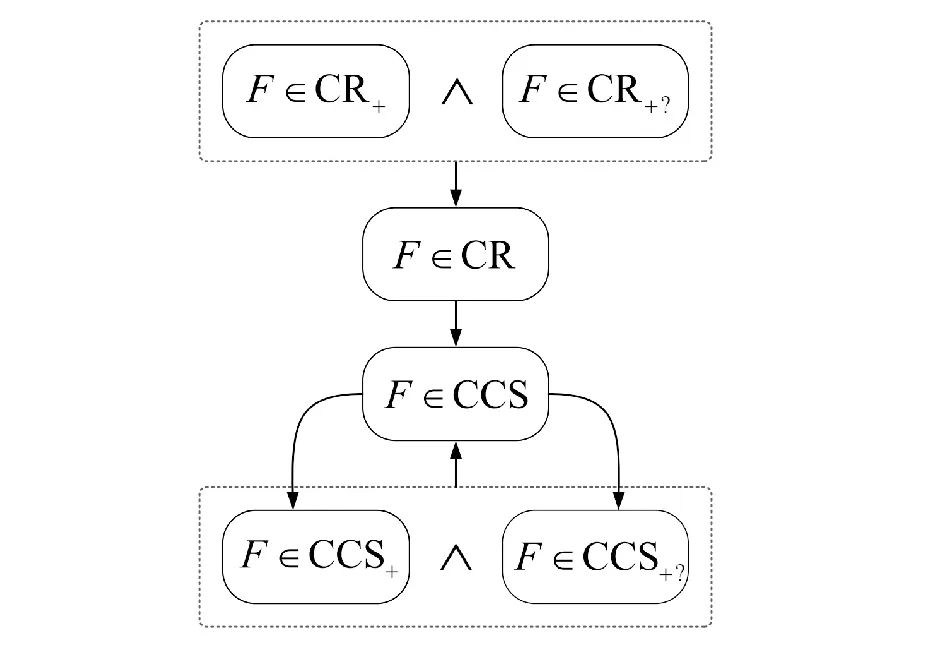
图2 3类SE-ISI概念约简的关系Fig.2 Relationships among three types of SE-ISI concept reducts

3 3类SE-ISI概念约简的获取方法

本节给出3类SE-ISI概念约简的代表概念矩阵和协调集判定定理,并在此基础上给出3类SE-ISI概念约简的计算方法。

首先定义3类SE-ISI代表概念矩阵。

定义8设IK=(G,M,{+,?,-},J)为不完备背景,L为其SE-ISI概念格,g∈G,m∈M,(X,[B,C])∈L。

1) 如果(g,m)∈X×B,则称(X,[B,C])是(g,m)关于SE-ISI概念的正信息代表概念,简称正信息SE-ISI代表概念,其全体记为REP+((g,m))。

2) 如果(g,m)∈X×C,则称(X,[B,C])是(g,m)关于SE-ISI概念的广义正信息代表概念,简称广义正信息SE-ISI代表概念,其全体记为REP+?((g,m))。

3)称REP((g,m))=

是(g,m)关于SE-ISI概念的关系代表概念集,简称关系SE-ISI代表概念集。

在此基础上,称Λ+=(REP+((g,m))),Λ+?=(REP+?((g,m))),Λ=(REP((g,m)))分别为IK的正信息SE-ISI代表概念矩阵、广义正信息SE-ISI代表概念矩阵及关系SE-ISI代表概念矩阵。

3类SE-ISI代表概念矩阵的相关性质如下。

性质1设IK=(G,M,{+,?,-},J)为不完备背景,g∈G,m∈M。Λ=(REP((g,m))),Λ+=(REP+((g,m)))与Λ+?=(REP+?((g,m)))分别为其关系SE-ISI代表概念矩阵、正信息SE-ISI代表概念矩阵和广义正信息SE-ISI代表概念矩阵。下列结论成立:

3) REP+((g,m))⊆REP+?((g,m))。

证明根据定义8,结论1)和结论2)显然成立。

结论3) 对任意(X,[B,C])∈REP+((g,m)),(g,m)∈X×B,又X×B⊆X×C,所以(g,m)∈X×C。由定义8知(X,[B,C])∈REP+?((g,m)),故REP+((g,m))⊆REP+?((g,m))。

事实上,要得到保持正信息不变的SE-ISI概念协调集,只需要找出与所有非空REP+((g,m))相交非空的SE-ISI概念集即可。保持广义正信息和保持关系不变的SE-ISI概念协调集也是类似的。即定理4所述。

定理4设IK为不完备背景,L为其SE-ISI概念格,F⊆L。下列结论成立:

1)F∈CCS+⟺∀REP+((g,m))≠∅,F∩REP+((g,m))≠∅;

2)F∈CCS+?⟺∀REP+?((g,m))≠∅,F∩REP+?((g,m))≠∅;

3)F∈CCS⟺∀REP((g,m))≠∅,F∩REP((g,m))≠∅。

2) 类似于结论1)的证明,可得结论2)成立。

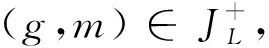
由定理4和性质1可得保持正信息不变的SE-ISI概念约简判定定理。

定理5设IK为不完备背景,L为其SE-ISI概念格。对任意F⊆L,若满足以下条件:

则F是保持正信息不变的SE-ISI概念约简。

保持广义正信息和保持关系不变的SE-ISI概念约简判定定理也可类似得到。

基于SE-ISI代表概念矩阵可给出SE-ISI概念约简的计算方法。

定义9设IK为不完备背景,L为其SE-ISI概念格。正信息SE-ISI代表概念函数定义为

φ(Λ+)=

∧REP+((g,m))∈Λ+(∨(X,[B,C])∈REP+((g,m))(X,[B,C]))。

根据吸收律与分配律,φ(Λ+)对应的最小析取范式的所有合取式为IK的所有保持正信息不变的SE-ISI概念约简。但通过φ(Λ+)计算时存在冗余的信息,因此记包含关系下所有极小REP+((g,m))组成的矩阵为最小正信息SE-ISI代表概念矩阵Λmin+,φ(Λmin+)对应的最小析取范式的所有合取式能更简单得到所有保持正信息不变的SE-ISI概念约简。类似可得φ(Λmin+?),φ(Λmin)。

例3(续例1)根据定义8,可得REP+((1,a))={(1,[abdeg,abdeg]),(14,[ab,ab])}={c2,c7}。类似地,可得到所有REP+((g,m))。因此,正信息SE-ISI代表概念矩阵为

Λ+=

最小正信息SE-ISI代表概念矩阵为

Λmin+=

进而正信息SE-ISI代表概念函数为φ(Λmin+)=(c2∧c5∧c4∧c3)∨(c2∧c5∧c4∧c8)。即CR+={{c2,c3,c4,c5},{c2,c4,c5,c8}}。类似地,可得CR+?={{c2,c3,c4,c5},{c2,c3,c5,c8},{c2,c5,c6,c8},{c2,c5,c8,c9}};CR={{c2,c3,c4,c5},{c2,c4,c5,c6,c8},{c2,c4,c5,c8,c9}}。

4 SE-ISI概念特征分析

本节根据SE-ISI概念在每种SE-ISI概念约简的作用将其分为3类,并研究其特征。

记Δ取“+”“+?”“R”分别表示保持正信息、保持广义正信息、保持关系不变这3类不同SE-ISI概念约简含义。

定义10设IK为不完备背景,L为其SE-ISI概念格,{FΔi|i∈τ,τ为指标集}为某类SE-ISI概念约简的集合。L可分为3类:

1) 核心SE-ISI概念集CΔ=∩i∈τFΔi;

2) 相对必要SE-ISI概念集KΔ=∪i∈τFΔi∩i∈τFΔi;

3)绝对不必要SE-ISI概念集UΔ=L∪i∈τFΔi。

式中,Δ∈{+,+?,R}。

例4表2为不完备背景(U,A,{+,?,-},S),其SE-ISI概念格如图3所示。其中,ci(i=1,2,…,10)是相应SE-ISI概念编号。将所有SE-ISI概念根据定义10分类,其结果如表3所示。

图3 SE-ISI概念格Fig.3 SE-ISI concept lattice

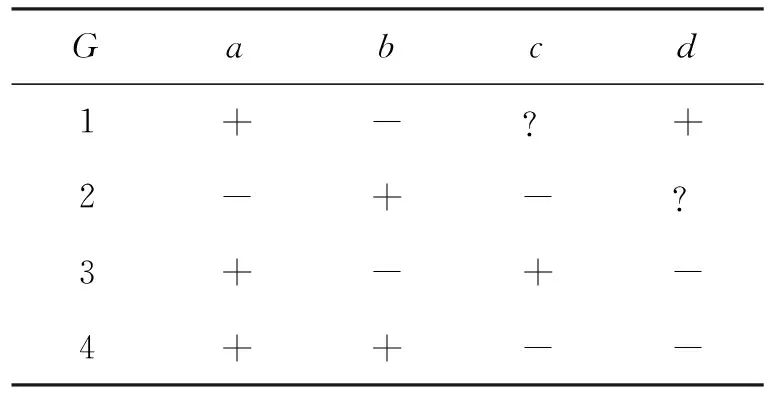
表2 不完备背景(U,A,{+,?,-},S)Tab.2 Incomplete context(U,A,{+,?,-},S)

表3 SE-ISI概念分类Tab.3 Classifications of SE-ISI concepts

从SE-ISI代表概念矩阵角度来说,SE-ISI概念在每类SE-ISI概念约简下的特征类似,故本文只给出保持正信息不变的SE-ISI概念约简下的3类SE-ISI概念判定定理。

定理6设IK为不完备背景,L为其SE-ISI概念格,c0∈L。下列结论成立:

2)c0∈U+⟺对任意REP+((g,m))∈Λmin+,有c0∉REP+((g,m));

2)必要性。假设存在REP+((g0,m0))∈Λmin+,使c0∈REP+((g0,m0)),由定理4知,存在F0∈CR+,使c0∈F0,即c0∉U+,矛盾。故对于任意的REP+((g,m))∈Λmin+,有c0∉REP+((g,m))。

充分性。假设c0∉U+,则存在F0∈CR+,使c0∈F0,即存在REP+((g0,m0))∈Λmin+,使c0∈REP+((g0,m0)),矛盾。故c0∈U+。

3) 由结论1)与结论2)直接可得。

定理7给出3类SE-ISI概念约简下核心SE-ISI概念集之间的关系。

定理7设IK为不完备背景,L为其SE-ISI概念格,有C+∪C+?=CR。

综上,C+∪C+?=CR。

3类SE-ISI概念约简下不必要SE-ISI概念集的关系,如定理8所述。

定理8设IK为不完备背景,L为其SE-ISI概念格,有U+∩U+?⊆UR。

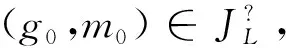
综上,c0∈UR,故U+∩U+?⊆UR。

例5(续例4)由表3可知,C+={c2,c3},C+?=∅,CR={c2,c3},U+∩U+?={c1,c10},UR={c1,c6,c10}。显然,C+∪C+?=CR,U+∩U+?⊆UR,即满足定理7和定理8。但c6∈UR,c6∉U+∩U+?,即UR⊆U+∩U+?不一定成立。

5 结语

本文针对不完备背景,提出了3类SE-ISI概念约简,研究了它们之间的关系,并基于SE-ISI代表概念矩阵给出了SE-ISI概念约简与SE-ISI概念特征的获取方法。不同的SE-ISI概念约简保留不完备背景的信息不同,根据所需信息选取SE-ISI概念约简后,可以减少SE-ISI概念的数量,在一定程度上可以降低用SE-ISI概念进行知识挖掘的复杂度。

事实上,每类SE-ISI概念约简数量并不唯一,那么对于每类SE-ISI概念约简,约简集间存在怎样的关系,以及如何通过评价指标衡量约简的优劣,将是进一步要研究的工作。