函数的概念与性质常见典型考题赏析
■张文伟 赵 昆
函数是高中数学的重要内容,也是每年高考的必考内容。在近几年的高考试题中,函数的概念与性质,幂函数的应用,分段函数问题等,一直都是常考点,且常考常新。下面就函数的概念与性质的常见典型考题进行举例分析。
题型一:函数概念的理解
判断对应关系是否构成函数的关键:一看自变量x的取值是否任意,二看对应的y是否唯一。判断两个函数是否相等,要根据函数的三要素来判断,即定义域、对应关系、值域,当三者都一致时,两个函数才是相同的函数。


题型二:求抽象函数的定义域
函数的定义域指的是自变量的取值范围;求函数f[g(x)]和f[h(x)]的定义域,可利用g(x)和h(x)的值域相等,列不等式求出x的取值范围;已知函数f(x)的定义域为[a,b],则复合函数f[g(x)]的定义域由不等式a≤g(x)≤b求得;已知复合函数f[g(x)]的定义域为[a,b],则函数f(x)的定义域为g(x)在x∈[a,b]上的值域。
例2 已知f(x+1)的定义域为(2,4)。
(1)求f(x)的定义域。
(2)求f(2x)的定义域。
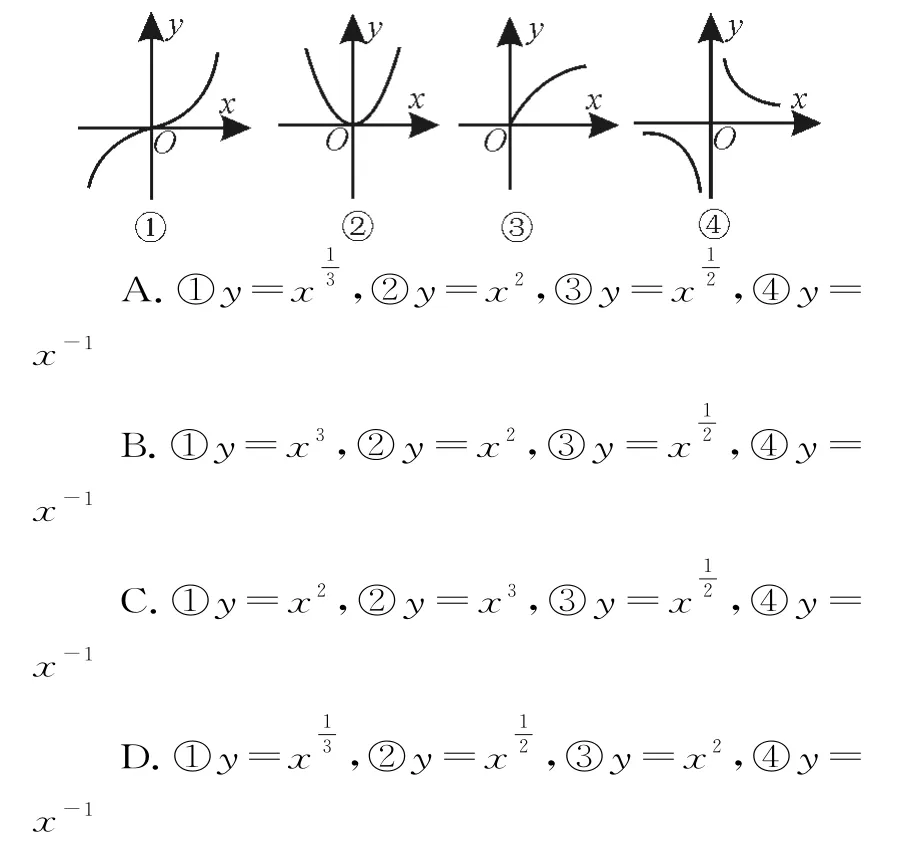
解:(1)因为f(x+1)的定义域为(2,4),所以2 求函数解析式的四种常用方法:待定系数法,当已知函数类型时,常用待定系数法;代入法,已知y=f(x)的解析式,求函数y=f[g(x)]的解析式时,可直接用新自变量g(x)替换y=f(x)中的x;换元法,已知y=f[g(x)]的解析式,求y=f(x)的解析式,可用换元法,即令g(x)=t,反解出x,然后代入y=f[g(x)]中,求出f(t)即得f(x);构造方程组法,当同一个对应关系中的两个自变量之间有互为相反数或者互为倒数关系时,可构造方程组求解。 跟踪训练3:根据下列条件,求f(x)的解析式。 (1)f[f(x)]=2x-1,其中f(x)为一次函数。 求分段函数的函数值时,一般应先确定自变量的取值在哪个子区间上,然后用与这个区间相对应的解析式求函数值;已知分段函数的函数值,求自变量的值,要进行分类讨论,逐段用不同的函数解析式求解,最后检验所求结果是否适合条件;实际问题中的分段函数,先以自变量在不同区间上对应关系的不同进行分段,再求出各个区间上的对应关系(解析式或图像)。 跟踪训练4:已知函数f(x)= 证明函数f(x)在区间D上的单调性应遵循四个步骤:设∀x1,x2∈D,且x1 用定义判断函数奇偶性的两个步骤:先求定义域,看是否关于原点对称;再判断f(-x)=f(x)或f(-x)=-f(x)是否恒成立。若已知函数的图像,则观察函数的图像是否关于原点或y轴对称,依此判断函数的奇偶性。 (3)f(x)=x2-x3的定义域为R。因为f(-1)=(-1)2-(-1)3=1+1=2,f(1)=12-13=0,所以f(-1)≠f(1),所以f(x)不是偶函数。因为f(-1)≠-f(1),所以f(x)不是奇函数。故f(x)=x2-x3既不是奇函数也不是偶函数。 (4)f(x)=|x+2|+|x-2|的定义域为R。因为f(-x)=|-x+2|+|-x-2|=|x-2|+|x+2|=f(x),所以f(x)=|x+2|+|x-2|是偶函数。 函数的单调性与奇偶性是函数的两大重要性质,解决函数问题离不开这两大性质的应用。奇函数在定义域内的关于y轴对称的两个区间上单调性相同,偶函数在定义域内的关于y轴对称的两个区间上单调性相反。 根据函数奇偶性的特点,即f(x)=±f(-x),将已知条件代入,从而可得f(x)的解析式;利用函数奇偶性求参数值的常用方法有定义法,特殊值法,函数的特点分析法,定义域关于原点对称法等。 例8 已知函数y=f(x)的图像关于原点对称,且当x>0 时,f(x)=x2-2x+3,则f(x)在R 上的表达式为_____。 形如y=f[g(x)]的函数为t=g(x),y=f(t)的复合函数,t=g(x)为内层函数,y=f(t)为外层函数,当t=g(x)单调递增,y=f(t)单调递增时,函数y=f[g(x)]单调递增;当t=g(x)单调递增,y=f(t)单调递减时,函数y=f[g(x)]单调递减;当t=g(x)单调递减,y=f(t)单调递增时,函数y=f[g(x)]单调递减;当t=g(x)单调递减,y=f(t)单调递减时,函数y=f[g(x)]单调递增。总之,简称为“同增异减”。求复合函数的单调性时,不能忽视函数的定义域。 对于分段函数在实数集R 上的单调递增(减)问题,除了保证在定义域的每一个区间上的单调性相同,还要考虑在分界点处的函数值的大小关系。若函数是增函数,则左边函数值小于或等于右边函数值(若函数是减函数,则右边函数值小于或等于左边函数值),这样才能满足R 上的单调递增(减),否则求出的参数范围会出现错误。对于定义域 提示:f(x)为R 上的减函数,当x≤1时,f(x)单调递减,所以a-3<0,即a<3。 已知函数最值或值域求参数的取值范围问题的关键是理解最值与值域的概念,注意结合函数图像容易求解。这类问题一般分为两类,一是参数在解析式中,二是参数在定义域中,解题时要注意参数对函数单调性的影响,一般要分类讨论求解。 解:(1)因为f(x)的值域为[0,+∞),所以y=mx2-2x+1 的值可取一切非负数。当m=0时,y=-2x+1,满足题意;当m>0时,只需Δ=4-4m≥0,可得0 综上所述,实数m的取值范围为[0,1]。 (2)由(1)知,当m∈[0,1]时函数值域为[0,+∞),满足最小值为0。当m>1 时,对于y=mx2-2x+1,显然Δ=4-4m<0,即值域不包含0,不满足题意;当m<0时,对于y=mx2-2x+1,显然Δ=4-m>0,即值域包含最小值0。 综上可知,实数m的取值范围为(-∞,1]。 跟踪训练11:若函数y=2x2-8x+9的定义域为[1,a],值域为[1,3],则a的取值范围为( )。 A.[1,2] B.(1,2] C.[2,3] D.[2,3) 提示:函数y=2x2-8x+9=2(x-2)2+1≥1 恒成立,其定义域为[1,a],值域为[1,3]。 当x=1时,y=3;当x=2时,函数y取得最小值1;当x=3 时,y=2×(3-2)2+1=3。 综上可得,a的取值范围是[2,3]。应选C。 对于幂函数y=xα(α∈R),在x∈(0,1)上,指数越大,幂函数图像越靠近x轴(简记为“指大图低”);在x∈(1,+∞)上,指数越大,幂函数图像越远离x轴(简记为“指大图高”)。由图像确定幂指数α与0,1的大小关系,需根据幂函数在第一象限内的图像来判断。利用幂函数的单调性比较大小时要注意:比较大小的两个实数必须在同一函数的同一单调区间内,否则无法比较大小。 图1 因为f(x)为二次函数,且图像的开口向上,对称轴为x=6,所以当x=6 时,函数f(x)取得最大值,且最大值等于440。 所以当销售价格定为6 元/kg 时,商场每日销售该商品所获得的利润最大,最大利润为440元。 跟踪训练13:某商店进货单价为45元,若按50元一个销售,能卖出50个,若销售单价每涨1元,其销售量就减少2个,为了获得最大利润,此商品的最佳售价应为每个_____元。 提示:设涨价x元,销售的利润为y元,则y=(50+x-45)(50-2x)=-2x2+40x+250=-2(x-10)2+450。 当x=10,即销售单价为60 元时,y取得最大值。答案为10。 分段函数是指在函数定义域中,对于自变量的不同取值范围有不同的对应法则的函数。分段函数主要是每一段自变量变化所遵循的规律不同,可以先将其当作几个问题,将各段的变化规律分别找出来,再将其合到一起,要注意各段自变量的范围,还要特别注意端点值的取舍。 (1)将利润表示为月产量的函数f(x)。 (2)当月产量为何值时,公司所获利润最大? 最大利润为多少元? (总收益=总成本+利润) 提示:(1)月产量为x台,则总成本为(20000+100x)元。 当x=300时,f(x)max=25000。 当x>400时,f(x)=60000-100x是减函数,f(x)<60000-100×400=20000<25000。 所以当x=300时,f(x)max=25000,即每月生产300 台仪器时利润最大,最大利润为25000元。 下面给出4 个幂函数的图像,则图像与函数的大致对应是( )。 提示:②的图像关于y轴对称,②应为偶函数,排除C,D。①的图像在第一象限内,图像下凸,递增得较快,所以幂函数的指数大于1,排除A。应选B。

题型三:求函数的解析式


题型四:分段函数的应用


题型五:函数单调性的证明及应用


题型六:函数奇偶性的判断


题型七:函数奇偶性与单调性的应用
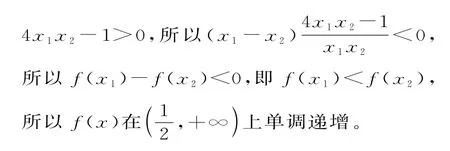
题型八:利用奇偶性求函数解析式或参数的值

题型九:复合函数的单调性

题型十:利用分段函数的单调性求参数的取值范围


题型十一:已知函数的最值或值域求参数的取值范围

题型十二:幂函数的图像与性质




题型十四:分段函数的模型问题