基于频域法的高速列车转向架附属设备随机振动疲劳寿命评估方法研究

何佳捷 ,袁盛铭 ,吴兴文 ,彭 波 ,李世杰 ,关 正 ,池茂儒

(1.中车青岛四方机车车辆股份有限公司 国家工程研究中心,山东 青岛 266111;2.西南交通大学 轨道交通运载系统全国重点实验室,四川 成都 610031;3.西南交通大学 机械工程学院,四川 成都 610031)

高速列车在运行过程中,轨道不平顺、钢轨波磨、车轮多边形、轮轨冲击、空气阻力、会车气流扰动以及其他外部环境都会使高速列车持续处在随机振动的状态。虽然随机振动产生的大多数结构响应应力远小于结构材料的静强度标准极限值,但是由于低幅值的循环应力引起的疲劳损伤会持续累积,最终造成的振动疲劳裂纹是机车车辆结构失效的主要形式。

频域寿命评估方法被广泛应用于结构随机振动疲劳寿命评估。频域疲劳计算方法通过结构薄弱位置处的应力功率谱,计算得到对应的雨流幅值概率密度函数,结合累积损伤理论和材料的S-N曲线,对结构的疲劳寿命和疲劳损伤进行评估。

频域寿命评估模型是保证评估准确性的重要因素。近几十年来,国内外学者提出多种常用的随机振动疲劳寿命频域法模型[1-7],如窄带法模型、Weibull分布模型、Dirlik分布模型等。但是,频域法模型的种类繁多,在相同的结构应力功率谱下使用不同方法的计算结果差异很大。所以,如何针对当前载荷和响应应力功率谱,选择一个合适的模型进行疲劳寿命评估是设计人员面临的难题。

本文以IEC 61373:2010《铁路应用车辆设备冲击和振动试验》[8]为据,在铁道车辆转向架附属设备主要承载频率范围内建立了不同谱参数的限带白噪声功率谱,并假设雨流幅值概率密度函数可以由Rayleigh分布模型和Weibull分布模型的加权组合近似。利用傅里叶逆变化方法和雨流计数法得到了对应功率谱的雨流幅值概率密度,研究了不同的谱参数与应力幅值概率密度函数之间的关系。提出了一种适用于转向架附属部件的频域法模型表达式,并分析了该模型对工程中常见的3种响应功率谱的拟合效果。最后设计了典型试验件的随机振动疲劳试验,验证了该模型的有效性。

1 雨流幅值概率密度函数模型研究

频域法的计算精度主要取决于雨流幅值概率分布模型的选择。本文在总结常用频域雨流幅值概率分布模型的基础上,结合随机过程理论,研究了适用于铁道车辆的雨流幅值概率分布模型。具体研究流程如图1所示。

图1 随机振动疲劳频域法模型研究流程图

1.1 常用频域雨流幅值概率分布模型

窄带近似分布模型(Rayleigh分布)[1]如式(1)所示:

Weibull分布模型[2]如式(2)所示:

Dirlik分布模型[3]如式(6)所示:

Lalanne分布模型[4]如式(14)所示:

Zhao-Baker分布模型[5]如式(16)所示:

Wirsching-Light修正系数法[6]如式(19)所示:

Tovo-Benasciutti修正系数法[7]如式(23)所示:

1.2 随机过程应力功率谱的设定

本文采用工程中最常见的限带白噪声功率谱对各种随机响应载荷谱进行近似模拟。典型的限带白噪声功率谱如图2所示。根据IEC 61373:2010标准可知,转向架及其附属设备的主要承载频率在5～250 Hz范围内。因此本文采用不同的中心频率、频带宽度和功率谱密度(Power Spectral Density,PSD)幅值组合,构造了81组限带白噪声功率谱,使频率范围覆盖0～300 Hz。

图2 典型的限带白噪声功率谱

图2中fc为中心频率,fr为频率范围,Gp为功率谱密度谱值。通过采取不同的参数组合,可以构造出拥有不同谱宽系数、中心频率和功率谱值的应力功率谱密度。限带白噪声随机过程的上限频率可以表示为fl=fc+fr/2,下限频率为fR=fc-fr/2,令r=fl/fR。

1.3 傅里叶逆变换模拟时域信号

根据帕塞瓦尔定理和功率谱密度函数的定义,可以用单边功率谱密度来描述平稳随机过程的统计特性[9],如式(26)所示:

对上式采用离散傅里叶变化得到离散化的功率谱密度:

式中:N=T/Δt,f k=k/(NΔt),k=0,1,2,…,N-1。

信号频谱的幅值可以表示为:

再由傅里叶变换理论,考虑相位服从0～2π均匀分布,可以得到信号频谱为:

式中:ϕk为信号频谱的相位角,k=0,1,2,…,N-1。

进而可以得到信号在时域下的模拟函数:

1.4 应力幅值概率密度函数模型参数拟合

在本研究中,假定雨流应力幅值的概率密度函数(Probability Density Function,PDF)结构是一个Weibull分布模型和一个Rayleigh分布模型的线性组合,前者主要对应小应力幅值部分,后者对应大应力幅值部分,他们之间通过一个权重系数来控制各自参与组合概率密度的比重,其表达式假定如式(31)所示:

式中:ω为Rayleigh分布和Weibull分布的权重系数,α为Weibull分布的形状参数,β1 为Weibull分布的尺度参数,β2为Rayleigh分布的尺度参数。

对不同工况下的雨流计数结果采用Levenberg-Marquarat+通用全局优化算法(LM-UGO)进行拟合。处理掉无效数据后对数据进行统计分析,得到ω、α、β1和β24个参数与应力功率谱之间的关系,如图3所示。初步判断权重系数ω和带宽系数呈指数关系;形状参数α是一个常数;尺度参数β1和带宽系数呈指数关系;尺度参数β2 和均方根值呈线性关系。假定4个参数与应力功率谱参数的关系如式(32)所示:

图3 参数拟合结果

根据式(32)中推测的参数与谱参数的关系,分别对4个参数进行数据拟合得到如表1所示的参数结果。

表1 推测参数与谱参数的拟合结果

根据上述参数拟合结果,给出雨流幅值概率密度函数模型各参数表达式如式(33)所示:

2 模型的拟合效果分析

2.1 模型对限带白噪声功率谱的拟合效果

限带白噪声功率谱的带宽系数对各模型的模拟精度影响较大,本小节主要分析在窄带和宽带情况下,上一节提出的频域法模型的拟合效果。设定中心频率为100 Hz,PSD 幅值为50 MPa2/Hz,通过改变频带范围来控制带宽系数的变化,拟合效果如图4所示。

图4 模型对限带白噪声功率谱的拟合效果

由图4可以看出,本文提出的模型(图4中的Newmodel)对于窄带限带白噪声功率谱有较好的拟合效果。随着带宽系数增大,功率谱从窄带谱转换为宽带谱,本文提出的Newmodal模型和Dirlik方法类似,可以模拟出PDF的小应力幅值区域的概率分布特征。

2.2 模型对单峰谱的拟合效果

单峰谱一般对应较小的频带宽度,所以主要分析在不同中心频率下本文提出的模型的拟合效果。选择PSD 幅值为50 MPa2/Hz,频带宽度为15 Hz,分析中心频率分别为50 Hz和200 Hz下模型的拟合效果,结果如图5所示。可以看出,随着中心频率的增加,频域法模型模拟的PDF逐渐向右偏移雨流计数结果,误差变大。其中,本文提出的Newmodal模型拟合得到的PDF在中低应力幅值部分略低于其他模型的概率密度,在大应力幅值部分略高于其他模型的概率密度。

图5 模型对单峰谱的拟合效果

2.3 模型对双峰谱的拟合效果

本文主要根据均方根比和中心频率距离2个参数分析模型对双峰谱的拟合效果。

(1) 不同均方根比下的模型拟合效果。根据实际工程中双峰谱的典型形式,选取第1个单峰的中心频率为60 Hz,频带范围为15 Hz,第2个单峰的中心频率为80 Hz,频带范围为5 Hz,PSD幅值为50 MPa2/Hz,分析了均方根比值为2和8下模型的拟合效果,结果如图6所示。可以看出,在不同的均方根比值下,本文提出的Newmodal模型都有较好的拟合效果,并且和Dirlik模型一样能拟合出小应力幅值峰值区域的特征。

图6 不同均方根比下的模型拟合效果

(2) 不同中心频率距离下的模型拟合效果。固定第1个频谱峰值的中心频率为60 Hz,频带范围为15 Hz,PSD 幅值为300 MPa2/Hz,第2个频谱峰值的频带范围为5 Hz,PSD 幅值为50 MPa2/Hz。分析了中心频率距离为20 Hz和40 Hz下模型的拟合效果,结果如图7所示。可以看出,本文提出的Newmodal模型对于具有2 个紧邻峰值的双峰功率谱拟合效果很好。但是随着中心频率距离的增加,频域法得到的小应力幅值峰值区域的结果向右发生偏差,误差变大。

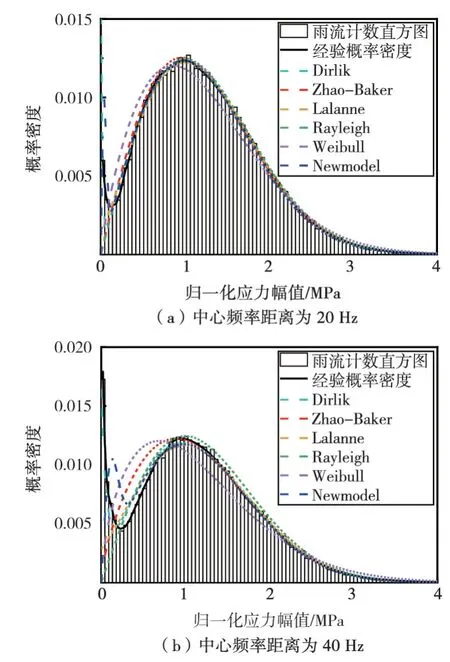
图7 不同中心频率距离下的模型拟合效果

3 随机振动疲劳试验验证

本文设计了悬臂梁形式的铝合金试验件,并设计了3种随机振动加速度功率谱对其进行随机振动疲劳试验。收集并处理危险部位的应力-时间历程数据,得到相应的应力功率谱密度函数。接着使用工程中的常用频域法模型和上一章节提出的频域法模型计算得到了试验件的疲劳寿命。最后采用不同模型计算得到的疲劳寿命和实际随机振动疲劳试验测得的寿命结果进行了对比,分析了频域法模型在实际工程中的计算精度,验证了本文提出的模型可靠性。

3.1 随机振动疲劳寿命频域计算方法

在频域法模型中,谱参数可以很好地表示随机过程的统计信息。谱宽系数ε和不规则因子γ是描述不同谱型时最常用的参数,他们都是谱矩m n(n=1,2,…)的函数,而谱矩是由功率谱与其对应的频率定义[10],其表达式为:

不规则因子γ为:

谱宽系数ε的表达式为:

谱宽系数ε的取值范围为0≤ε≤1。当谱宽系数ε接近0时,对应理想窄带随机过程;当ε接近1 时,对应白噪声随机过程。

根据Miner线性累积损伤理论[11],结构的疲劳损伤可以表示为:

式中:n i为应力水平为S i时的实际循环次数,N i为材料S-N曲线应力S对应下的寿命。

对于连续状态,在时间T内和应力范围(S i,S i+ΔS i)内的应力循环次数为:

式中:P(S i)为应力幅值概率密度函数中某一应力幅值对应的概率密度值,E(P)为单位时间内应力循环次数,可以由式(39)得出:

若已知材料的S-N曲线:N=kS-b,可以得到振动损伤的表达式为:

按照Miner线性累积损伤理论,当损伤值D等于1时结构发生破坏,此时疲劳寿命t为:

3.2 试验方案

本文将试验件设计为带有圆形弧的悬臂梁形式,试验件具体形状和尺寸如图8所示。

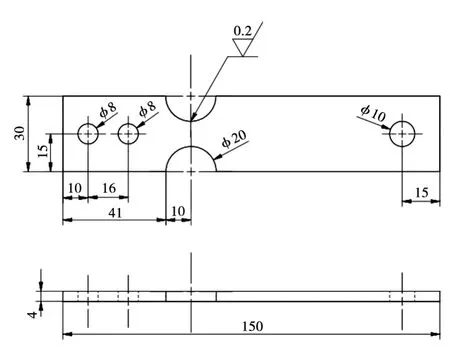
图8 试验件具体形状和尺寸示意图

试验件的材料选用的是5083铝合金,板材的厚度为4 mm。5083铝合金材料性能如表2所示。

表2 5083铝合金的机械性能

为了保证随机振动疲劳试验的稳定进行,设计了夹具将试验件固定在随机振动台上。夹具选用6061铝合金材料制造,包括基座和压片两部分。压片的主要作用是为了避免在螺栓和试验件连接处产生大的应力,对疲劳试验结果产生影响。

同时,为加速随机振动疲劳试验过程以达到缩短试验时间的目的,采用螺栓穿过试验件端部的孔并和螺帽固定在一起的方式来模拟集中质量,螺栓和螺母的总重量为26 g。试验件通过夹具连接在试验台上的整体情况如图9所示。

图9 试验件安装在振动台上示意图

3.3 试验过程

试验一共设计了3种疲劳载荷下的随机振动疲劳试验,疲劳载荷均以限带白噪声功率谱的形式给出,3种疲劳载荷分别记为A1、A2和A3,频率覆盖30～300 Hz,激励功率谱幅值分别为9.6(m/s2)2/Hz、14.4(m/s2)2/Hz和19.2(m/s2)2/Hz,激励功率谱如图10所示。

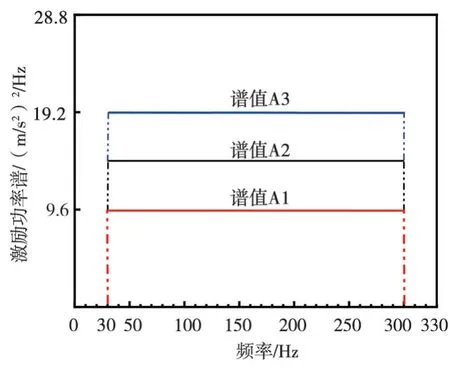
图10 随机振动疲劳试验的激励功率谱

试验测得的数据为通过应变片记录的应变时间历程和疲劳破坏吋间。将应变信号换算为应力信号后,使用MATLAB 软件中的Welch 法进行数据处理。Welch法中的窗口长度取1 024 mm,得到在上述3种加速度激励谱输入下,试验件危险部位的响应应力功率谱。3种载荷下的应力时域数据和应力功率谱数据如图11～图13所示。

图11 疲劳载荷谱A1下的试验数据

图12 疲劳载荷谱A2下的试验数据

图13 疲劳载荷谱A3下的试验数据

3.4 试验结果分析

在随机振动疲劳试验中,试验件疲劳损坏的形式为直接断裂。本次试验将发生突变的时刻记录为试验件的疲劳破坏的寿命时间,图14为在试验中记录的某一试验件薄弱位置的应力-时间历程。随机振动疲劳寿命试验结果如表3所示。

表3 随机振动疲劳寿命试验结果 min

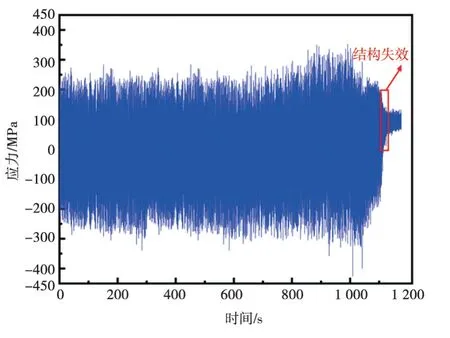
图14 试验件薄弱位置的应力-时间历程

将3种随机振动载荷谱下试验件危险部位的应力功率谱结合频域法计算得到对应的应力幅值概率密度函数。同时对应力-时间历程数据使用雨流计数法,得到雨流幅值概率密度函数,如图15所示。

图15 试验件危险位置应力幅值概率密度函数

得到3种随机载荷下结构的PDF后,结合材料的S-N曲线和Miner线性累积损伤理论,评估试验件的理论疲劳寿命。S-N曲线选取IIW 标准[12]中的铝合金母材的参数。随机振动疲劳试验的结果如表4 所示,表中的WL 代表Wirsching-Light修正方法,TB代表Tovo-Benasciutti修正方法。

表4 疲劳寿命计算结果和误差

本文将不同计算结果与试验数据进行对比如表4所示。由表4可以看出,各种随机振动疲劳寿命频域方法的计算结果都偏向于保守。其中,时域法的计算结果精度最高。在频域法中,本文提出的Newmodal模型方法计算得到的寿命相对误差最小,证明了本文提出的模型的有效性和可靠性。Wirsching-Light修正方法的相对误差也很小,其他几种工程中常用的模型的计算误差都在10%左右,其中Dirlik、Zhao-Baker、Lanane模型的计算结果相近。

4 结论

本文依据IEC 61373:2010标准在铁道车辆转向架附属设备主要承载频率范围内建立了不同的形式的限带白噪声功率谱。选取Rayleigh 分布模型和Weibull分布模型加权组合的形式进行了频域法模型的研究,通过数据拟合得到了不同的谱参数与应力幅值概率密度函数之间的关系。并分析了模型对常见的3种形式应力PSD 的拟合效果。最后设计了随机振动疲劳试验对模型的有效性进行了验证,得出以下结论:

(1) 本文提出的频域法模型中的权重系数ω和带宽系数呈指数关系;形状参数α是一个常数;尺度参数β1和带宽系数呈指数关系;尺度参数β2和均方根值呈线性关系。

(2) 本文提出的模型对于窄带限带白噪声功率谱有较好的拟合效果。在PSD 为宽带谱时,本文提出的模型可以模拟出PDF 的小应力幅值区域的概率分布特征;对于单峰谱,随着中心频率的增加,频域法模型模拟的PDF逐渐向右偏移雨流计数结果,误差变大。其中,本文提出的模型拟合得到的PDF在中低应力幅值部分略低于其他模型的概率密度,在大应力幅值部分略高于其他模型的概率密度;本文提出的模型对于在不同的均方根比值的双峰谱模型都有较好的拟合效果,对于具有2个紧邻峰值的双峰功率谱有较好的拟合效果,但是随着中心频率距离的增加,频域法得到的小应力幅值峰值区域的结果向右发生偏差,误差变大。

(3) 各种随机振动疲劳寿命频域方法的计算结果都偏向于保守。本文提出的模型方法计算得到的寿命相对误差最小,证明了本文提出的模型的有效性和可靠性。Wirsching-Light修正方法的相对误差也较小,其他几种工程中常用的模型的计算误差都在10%左右,其中Dirlik、Zhao-Baker、Lanane模型的计算结果很接近。