核心素养视域下初中数学思辨能力培养策略研究
陈银娟
一、 初中数学思辨能力培养的现状及意义
当下初中生探析数学的能动性不高,动手操作能力不强,探析方法不够灵活,数学的思辨能力较弱,而数学核心素养中至关重要的一部分就是数学的思辨能力。所以,教师要针对现有核心素养的要求对自身教学进行必要的改变,使教学更符合学生的实际和培养的目标。学科核心素养的落实是学生核心素养养成的重要抓手,所以数学核心素养的养成需要教师在学科教学中有目的的培养。经过经年积淀,学生核心素养的发展才能聚沙成塔。
二、 核心概念的界定
思辨能力就是善于思考巧于审辨的能力,所谓思考指的是对复杂问题严于推理、果于判断、精于辨析的逻辑活动,其中的审辨指的是深入分析、审判、辨别事物内在关联或异同等。在传统的数学教学中,教师只注重了“温度”忽视了“深度”,难以给学生提供深度思考的平台。所谓深度教学就要求教师挖掘教学素材深度,切实地了解学生的实际情况,设计合理题组,让学生进行深刻的思维训练,通过问题链和自主探究活动进行深刻思维交流,让学与教的过程,成为一个深度探索的过程,一个发现、分析、解决问题的过程,一个深度重思辨能力培养的过程,从而学生有更多的思辨机会,感受到思辨之美,建立合理知识结构。
三、 深度提升初中数学思辨能力的主要途径
(一)探究深度教学策略,提升学生数学思辨能力的深度
初中数学学科具有逻辑性与抽象性等特点,所以教师教学预设、教学深度的把控就显得尤为重要。教师的功能就是在把握核心素养的前提下,把预设的教学内容与学生已有的知识存储联系起来,帮助学生从实物的外在延展到本质,促使学生思辨能力得到发展。
数学思辨训练要求教师搭建载体,通过类比、辨析,在解决问题的过程中不断引导学生,日积月累的积淀过程,就是学生思辨能力日益提高的过程。
1. “由简到难”循序渐进的思辨
在数学教学的过程中,建立探索梯度,设置思维训练题组,由简入繁,由易到难,思维训练效果往往比较明显。
【例1】如图,已知直角三角形△ABC中,∠C=90°,AC=8,BC=6,一个正方形放置在三角形内部,并且点E、F分别在直角边上,求正方形的边长。
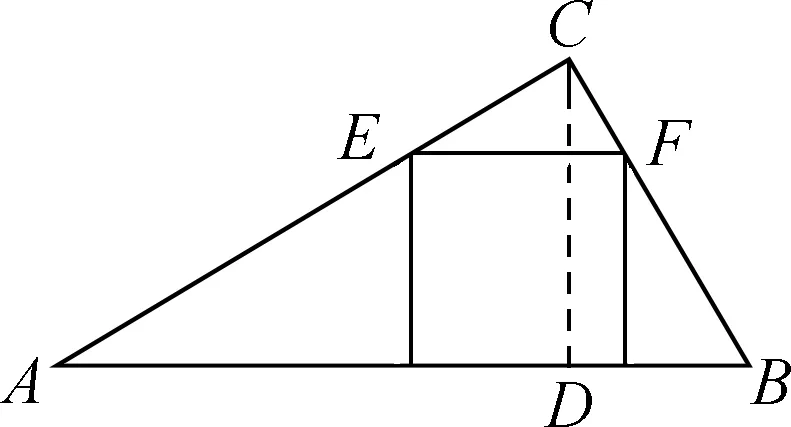
拓展一:两个完全相同的正方形放置在三角形内部,并且点E、点F分别在直角边上,求正方形的边长。
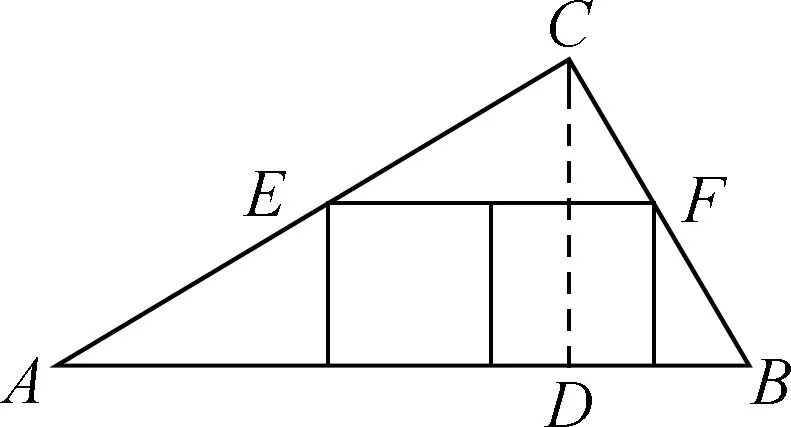
拓展二:如果摆放n个相同的正方形呢?
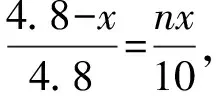
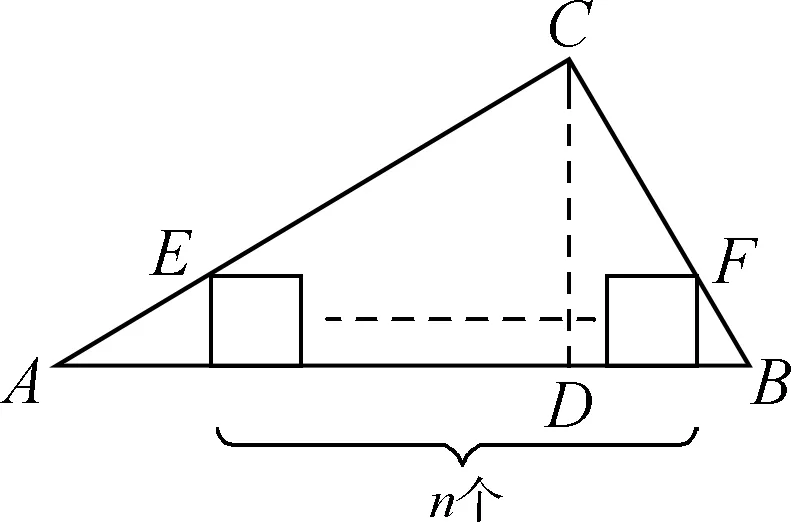
拓展三:如果用半圆替换正方形,又可以得到怎样的结论?
2.“由此及彼”,从特殊到一般的思辨
【例2】分别以直角三角形三条边长向外做正方形,由勾股定理可得:以斜边为边长的正方形的面积正好等于两个直角边为边长的正方形的面积之和,即S3=S1+S2(如图1)。那么,如果正方形改成正三角形(如图2)呢?是否存在S3=S1+S2呢?
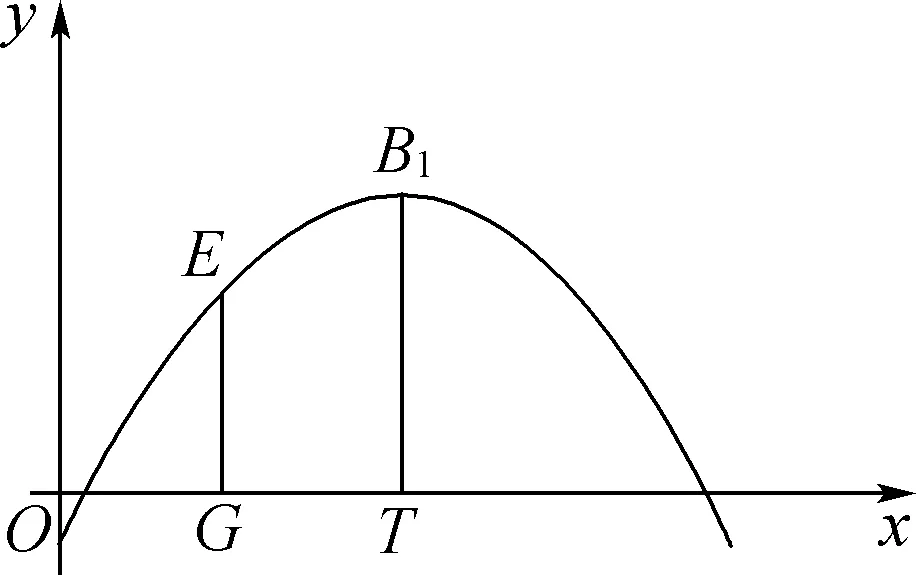
图1
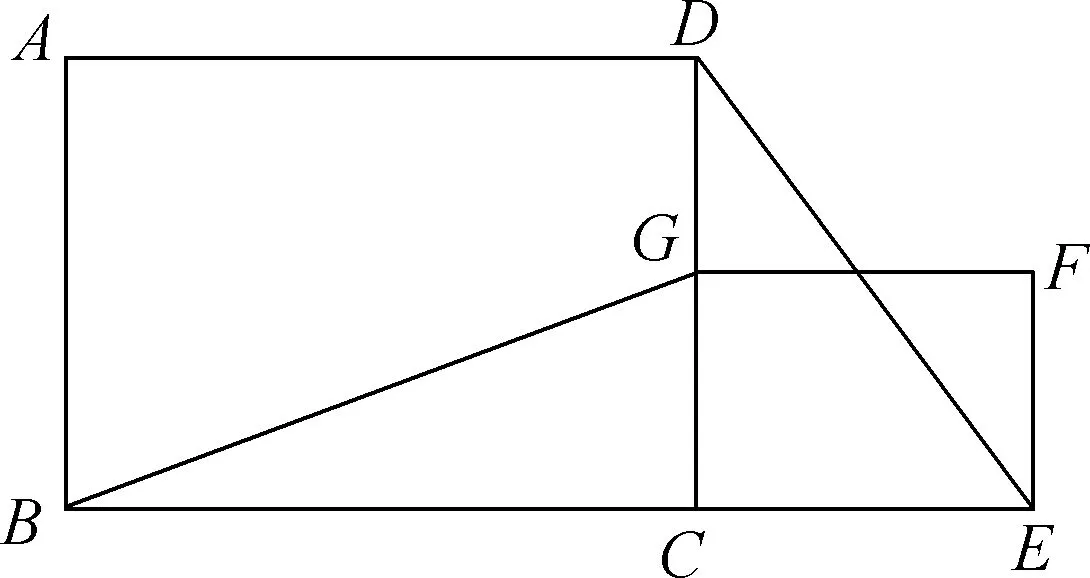
图1
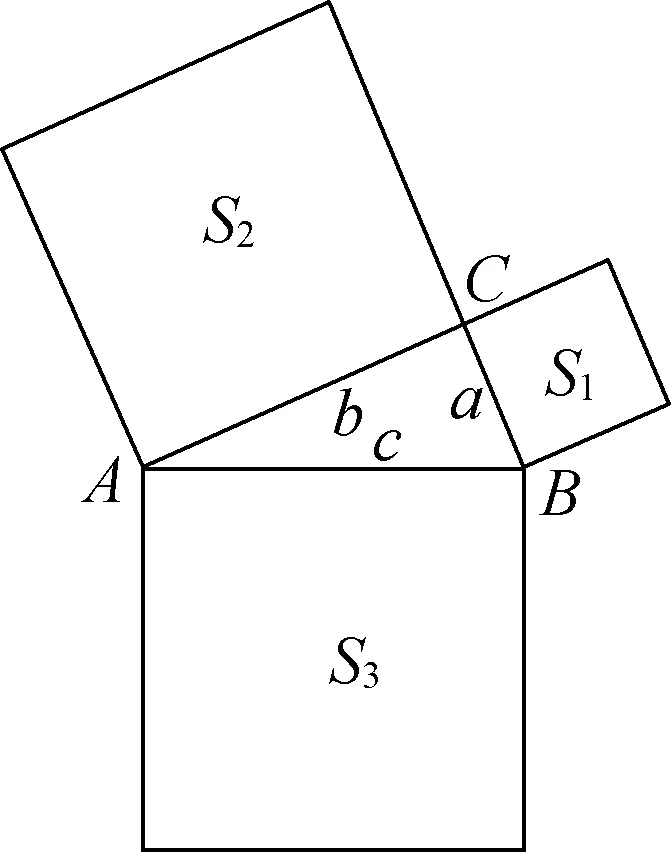
图1

图2
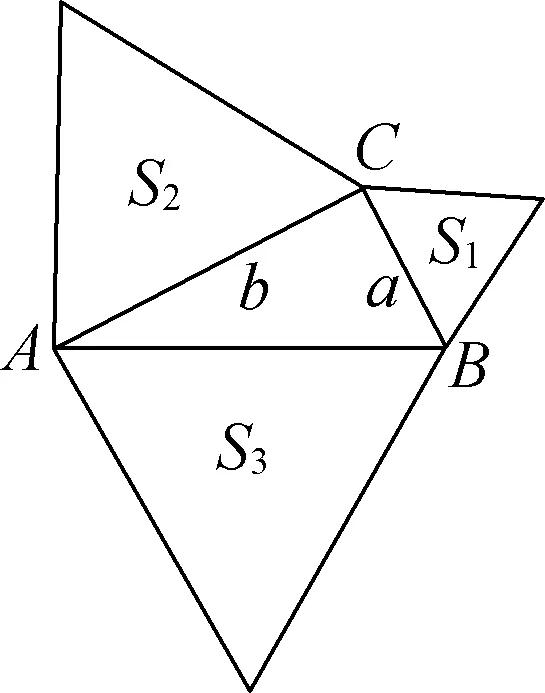
图2
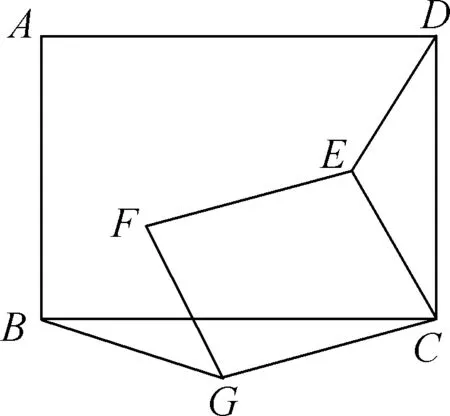
图3
根据勾股定理和等边三角形的性质,以直角三角形的三条边作正三角形,S3=S1+S2同样满足;如果用半圆代替正方形呢?
(二)探究深度教学策略,提高学生数学知识结构深度
在核心素养要求下,教师应树立新的教学理念,摒弃灌输式的教学模式,积极引导学生勤思辨,教师可以通过按章建序,引导学生画知识网络图,帮助学生深度理解不同知识点的联系,形成科学的知识结构,使学生梳理水平得到提高,归纳能力得到提升。
【例3】如下图中横线上①②两个序号分别表示条件是:①两组对边分别平行;②有且只有一组对边平行。请对下图横线上的其他6个数字写出相应的条件。
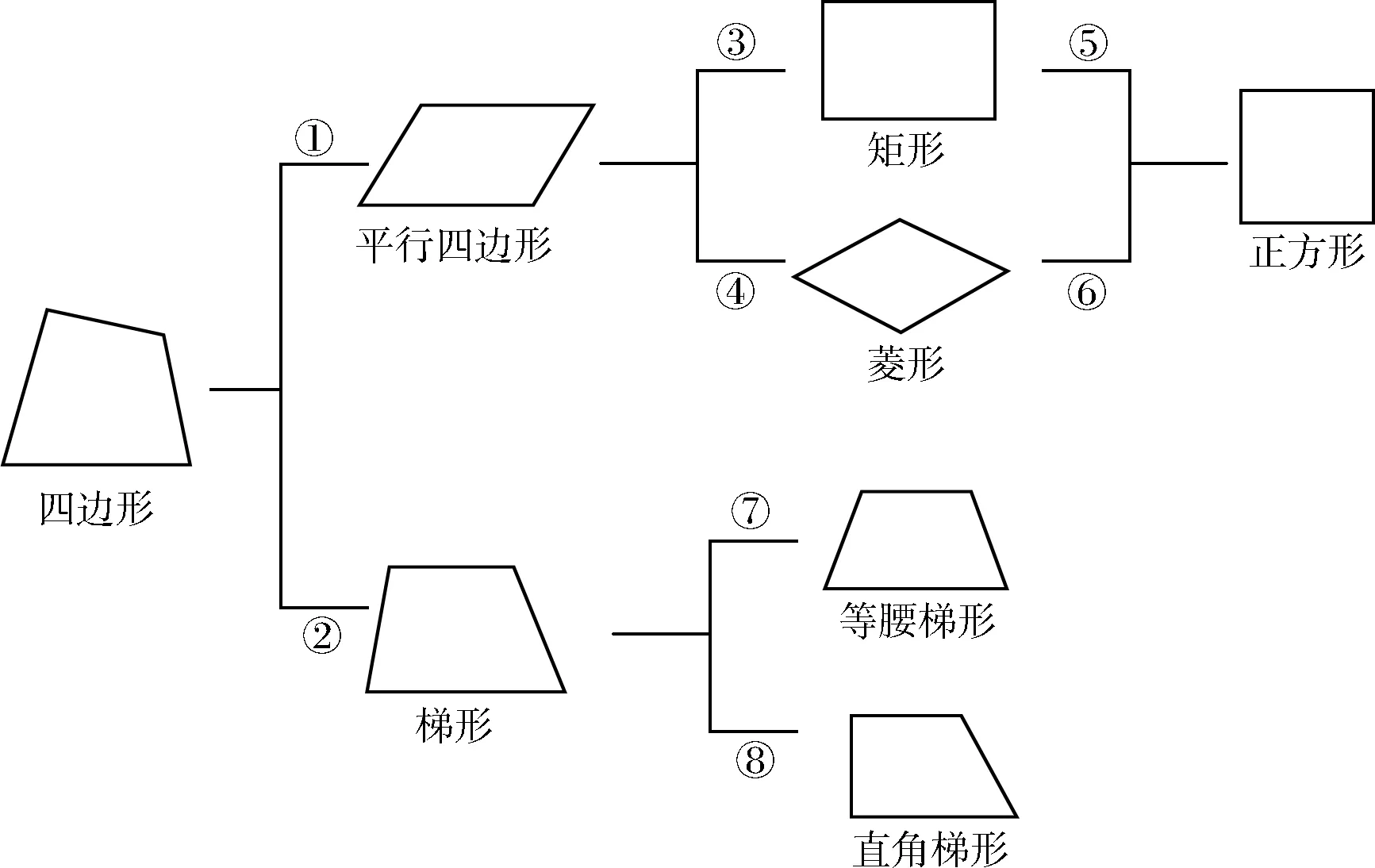
通过认识内在联系之间的差异来熟悉各种特殊的四边形,逐步丰富概念内涵,可以让学生能够在这个过程当中,对自己的知识结构进行构建,摒弃死记硬背的机械式学习方法,做到对四边形之间关系的深入理解,把散乱的知识点形成了链接式的知识面,思辨所学知识的内在联系。
【例4】已知三角形ABC中,AB=AC,其中AC上的高线BE与AB的夹角是50°,求该三角形顶角的度数。
从思维的全面性角度有意识强化训练,学生的思维全面性更强,质疑习惯和质疑能力也会在训练中逐渐养成。
(三)探究深度教学策略,提高学生数学知识能力深度
抽象知识在思维冲撞和不断反思、提高中逐渐内化为学生的实践能力,让学生具备这方面的能力,从而更好地深度学习或构建数学知识体系,达到能力的不断深化。
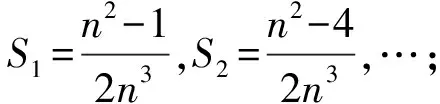
( )
四、 初中数学思辨能力培养的主要方法
(一)创设思辨深度学习情景
通过创设情景思辨,逐步由浅入深的类比,易获得数学的模型和本质。例如,笔者在教学七年级上册&3.2《合并同类项》一课时,做了如下的尝试。
1.观察实物,并对物品进行分类
教师把食品(形状有圆形、方形、三角形)、几何模具、玩具、学习用品摆放在一起,让学生按照自定的标准进行分类,教师提问:①怎么分?②为什么这样分?③若分类标准一样,分类的结果是否唯一?
2.观察多项式,并对项进行分类
观察多项式-3x+9y-2z+3x-4y,教师提问:①你想把哪几项归为一类?②分类的依据是什么?那么5a2b-3ab2-6+2a2b+3ab2+4ab-8ab+10呢?
生活中的分类是学生所熟悉的,由物品思辨到同类项的思辨,可以使学生觉得数学并不神秘与陌生,把日常生活中常见的方法使用在比较抽象的数学中,对提高学生数学学习兴趣和思维能力提升意义重大。
(二)开展深度思辨的教学对话活动
列尔耐尔说“问题教学的本质在于学生由教师经常引入寻求有根据地解决对他们来说是新问题的办法的过程,由此他们就学会独立地获取知识、运用原先学过的东西和掌握从事创造性活动的经验。”所以在课堂教学中创设深度思辨对话活动,有利于学生在独自遇到问题时,开展深度的探究。
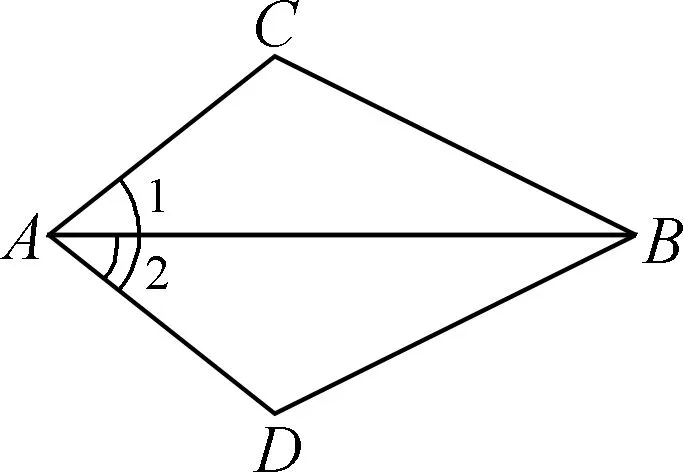
【例6】如图,要证明△ABC≌△ABD,已知∠1=∠2,还需补充一个条件,共有多少种添法呢?作为一个探究性问题来研究,先让学生呈现出自己所想的方法,先不管它哪些是成立的,哪些是不成立的,根据已学知识,对学生的方法逐一地进行评判,最后做取舍,这样效果会好得多。
学生先思考后提出自己的意见,然后老师引导学生根据已有的经验进行探究。碰到新的问题时,在铺垫探究知识与方法后,激发学生强烈的探究欲望,这样的课堂高效、富有激情。
(三)创设复习课中数学的思辨教学活动
在复习课教学中,由一道例题出发,通过变式形成题组,将知识点的落实与思辨能力的提升相结合,这一过程对学生知识的掌握以及解题能力的提高作用很大。
问题1:在直角坐标系中,A(2,2),B(5,4),C(8,2)求经过A、B、C三点的抛物线解析式。
问题2:若将问题1中的抛物线绕顶点旋转180°,再向上平移2个单位长度,①你能求出所得抛物线的解析式吗?②如图1所示,作B1T⊥x轴于T,点P在x轴上,EP⊥x轴交抛物线于E,若TP=3,求PE的长。
问题3:如图2所示,某隧道拱顶E-B-F段为上题中所求抛物线的一部分,最高点B1距地面4米,点E和点F到地面的距离相等,EF两点水平距离为5.6米。若该隧道允许通过的最大车子是宽为2米,高为3米的大巴车,问能否将此隧道改建为双车道?
优化后的例习题将思辨过程分解在问题组中,不仅利于基础的巩固,更有助于培养学生灵活运用的能力,使基础训练层级化,能力培养有梯度,达到多元化复习的目标。
(四)培养深度的思辨质疑能力
深度的质疑能力是学好初中数学必需的能力,数学教学中,教师可通过变式与拓展例题,辨析解题的思路异同,从而培养学生深度的思辨质疑能力。
原题:如图,点C是线段BE上任意一点(不与BE重合),点A、D两点在BE的同侧,分别作以BC、CE为边,作等边△ABC和△DCE,连接AE、BD,求证:BD=AE;教师以此题为母题适当的变化、拓展,设计出题组。
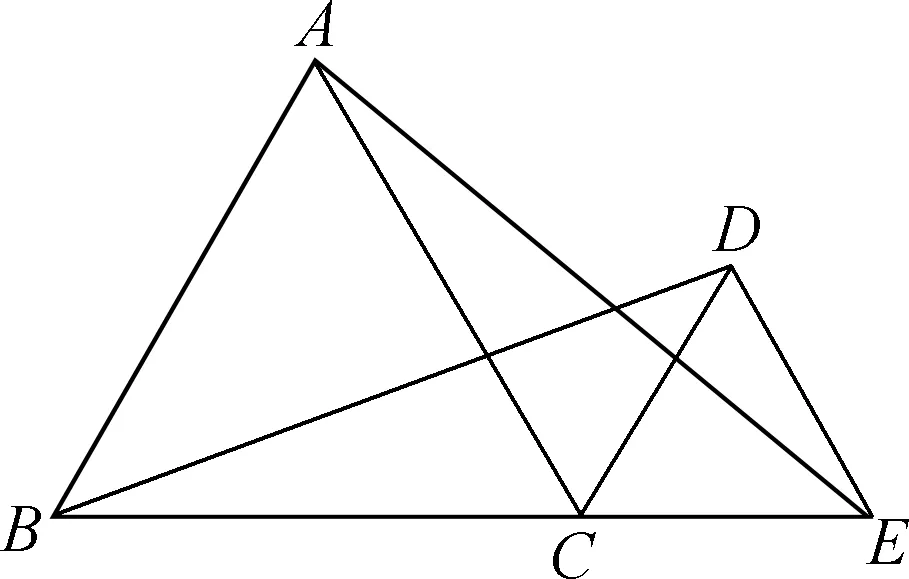
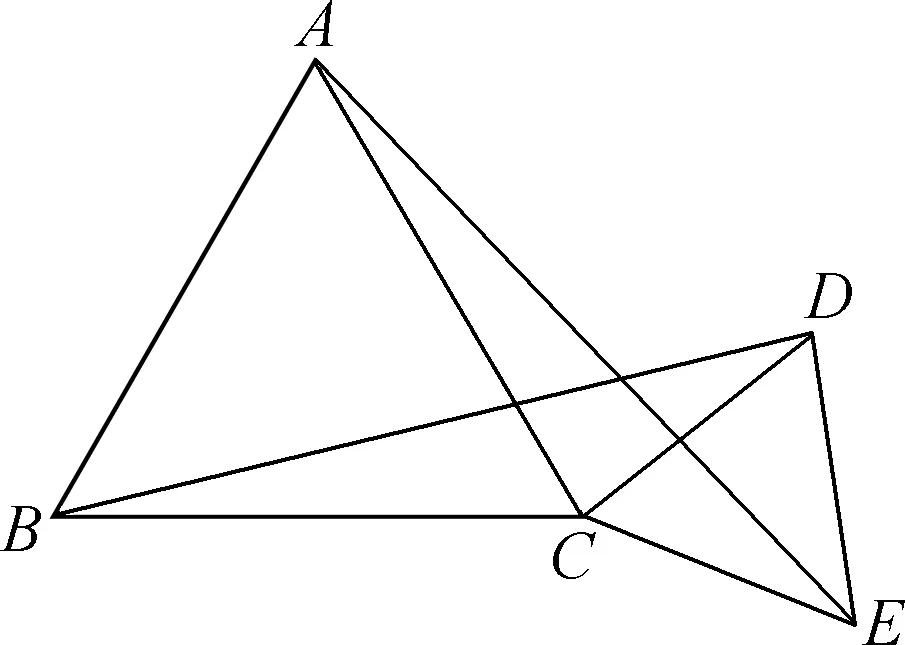
变式一:将题中“点B、点C、点E在一条线上”这一条件改成“将△DCE绕C点顺时针转一定角度”,其他不变(如图)。
变式二:用“两个正方形”替换原题中“两个等边三角形”,G是正方形CD边上的一个动点,正方形CEFG是以CG为一边的正方形,连接BG,DE,求线段BG、线段DE的数量关系。
变式三:正方形GCEF绕着点C旋转得到的,上题的结论仍成立吗?学生尝试画图并选取其中一图证明你的结论。
一道典型的例题,通过图形的变化,图形的移动,或者图形的组合,就可变为新题型,这些可以让学生在变化中寻求共性,在运动中考虑静态的联系,使考查思辨的深度逐渐提高,学习的效率增强,应用能力提升。
五、 结论
思辨活动是一种深度的学习探究活动,它改变了传统的教学,避免了被动地接受、浮于表面、理解不深透、知识体系不严密等弊端。教师有意识地启发和引导,为学生搭建思辨的平台,学生可以通过积极的思辨过程,感知规律,建立知识体系,应用数学模型等。这种学习不仅有利于教师的专业成长,更有利于学生获取数学知识、技能和能力以及思维品质、创新思维、创新能力培养。

