基于SSA-LSTM组合模型的城市轨道交通短时客流预测

姜嘉伟 赵金宝 刘文静 徐月娟 李明星

摘要：隨着我国经济的快速增长及城市化水平的不断提高，轨道交通在居民出行中发挥着越来越重要的作用。作为影响城市轨道交通运营效益和服务水平的关键因素，客流精准预测受到运营管理者和研究者的日益重视。为提高城市轨道交通客流预测精度，提出了基于麻雀搜索算法（SSA）和长短期记忆网络（LSTM）的SSA-LSTM组合模型。本文以杭州地铁一号线客流量数据为例，在选取轨道交通客流相关影响因素的基础上，利用建立的SSA-LSTM模型对相关站点进行短时客流预测，并与LSTM模型、遗传算法（GA）优化的LSTM模型（GA-LSTM）以及粒子群算法（PSO）优化的LSTM模型（PSO-LSTM）预测结果进行对比分析。结果表明，相比于前述参照模型，SSA-LSTM模型的预测精度分别提升了19.1%、9.7%和2.4%，并在均方根误差指标方面有更优异的表现。SSA-LSTM组合模型在城市轨道交通客流预测中具有一定的应用价值，具有协助运营管理者提高城市轨道交通运营管理效益和提高服务水平的潜力。

关键词：城市轨道交通；短时客流预测；麻雀搜索算法；长短期记忆网络；组合模型

中图分类号：U231   文献标志码：A   文章编号：1002-4026（2023）05-0075-10

Short-term prediction of urban railtransit passenger flow based on the Sparrow

Search Algorithm-Long Short Term Memory combination model

JIANG Jiawei1，ZHAO Jinbao1，2*，LIU Wenjing1，XU Yuejuan1，LI Mingxing1

（1. School of Transportation and Vehicle Engineering， Shandong University of Technology， Zibo 255000，China;2. School of Transportation， Southeast University， Nanjing 210009，China）

Abstract∶With the rapid growth of China′s economy and the continuous urbanization， rail transit plays an increasingly important role in residents′ travel. As a key factor affecting the operation efficiency and service level of urban rail transit，accurate passenger flow prediction has attracted increasing attention from operation managers and researchers. To improve the prediction accuracy of the urban rail transit passenger flow， this paper combines sparrow search algorithm （SSA） and long short-term memory network （LSTM） and proposed a SSA-LSTM combined model. Based on the passenger flow data obtained from four stations of Hangzhou Metro Line 1 and the selected factors affecting the rail transit passenger flow， we used the proposed SSA-LSTM model to predict the short-term passenger flow of relevant stations. Then， we compared the predicted results with those estimated by the LSTM， GA-LSTM， and PSO-LSTM models. Results show that the prediction accuracy of the proposed model is 16.0%， 8.8%， and 2.3%， higher than the aforementioned models， respectively; furthermore， the proposed method exhibited better performance in terms of the root mean square error. Thus， the proposed model has potential applicationin predicting the urban rail transit passenger flow. Moreover， it can assistoperation managers in improving the operation efficiency and service level of urban rail transit.

Key words∶urban rail transit; short term passenger flow prediction; sparrow search algorithm; long short term memory network; combined model

随着经济的快速增长、城市化水平的不断提高以及小轿车保有量显著增加，交通拥堵、污染严重等一系列城市交通问题日益凸显。为引导城市健康、可持续发展，越来越多的城市愈发重视优先发展大容量公共交通尤其是城市轨道交通。作为影响城市轨道交通运营效益和服务水平的关键因素，城市轨道交通客流预测尤其是短时客流精准预测受到运营管理者和研究者的日益重视。

城市轨道交通短时客流具有规律性较差、非线性特征显著等特点，传统模型如ARIMA（autoregressive integrated moving average）预测时会产生较大误差，诸多学者通过探索建立新模型以提高预测精度。施雪蓉等[1]通过对比随机森林、BP（back propagation）神经网络、长短期记忆神经网络（long short-term memory，LSTM）在轨道交通流客流精度表现发现LSTM模型拟合结果更好；吕秋霞等[2]利用双向LSTM模型并通过调整模型步长，发现双向LSTM模型较LSTM预测精度更高；赵明伟等[3]建立了改进粒子群优化算法（IPSO）-LSTM模型（IPSO-LSTM），通过增加动态自适应惯性权重防止陷入局部最优，结果显示IPSO-LSTM模型精度更高；Shivaraj等[4]利用城市轨道交通自动售检票系统（automatic fare collection system，AFC）系统，基于LSTM模型使用季节自回归移动平均模型对客流进行预测，研究结果表明，该模型可以更好地应用于发展中国家的交通状况；Guo等[5]针对异常客流预测难度大等问题，建立了支持向量机（support vector machine，SVM）-LSTM（以下简称SVM-LSTM）组合模型，对比结果表明，SVM-LSTM模型具有优异的反应灵敏度和预测精度。

通过查阅相关文献发现，已有研究主要通过将时间序列及神经网络与其他模型算法相结合等方式提高城市轨道交通短时客流预测精度。针对城市轨道交通短时客流特点和传统全局寻优算法收敛速度相对较慢的缺陷，本文将新兴的麻雀搜索算法（sparrow search algorithm， SSA）与LSTM相结合，构建SSA-LSTM组合模型，结合杭州地铁一号线客流量数据验证该组合模型的可用性和有效性。

1 SSA-LSTM模型

1.1 麻雀搜索算法

麻雀搜索算法（SSA）是受麻雀觅食和反捕食行為启发而提出的新型全局寻优算法[6]。相比于其他优化算法，SSA具有更高效的寻优效率以及强大的收敛功能等特性。SSA的基本建模步骤包括：

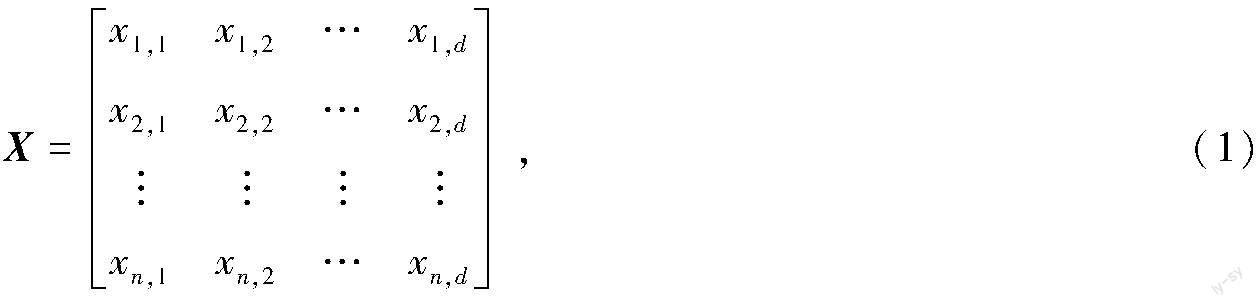
（1）构建种群。由n只麻雀组成的种群可表示为

其中，n表示麻雀种群数量，d表示待优化问题维度。

（2）计算适应度值。

其中，f表示每个麻雀的适应度，适应度函数选取训练集与测试集整体的均方误差平均值。

（3）更新发现者位置。在SSA算法中，发现者为种群提供觅食方向，其位置更新描述见式3：

其中，t为迭代次数，xti，j为t次迭代第i只麻雀j维度值，可视为待优化问题不同参数。tm为预设最大迭代次数，Q为标准正态分布随机数，L为全1的1×d矩阵。R2和T0分别为安全阈值和警报阈值。当R2T0时，表明种群中警戒者发现危险，发现者会停止觅食，飞往安全位置。

（4）更新追随者位置。在SSA算法中，发现者和追随者的身份会发生转变，但两种身份比例在种群内固定不变，每代中适应度高的前m只麻雀作为发现者，n－m只麻雀作为追随者。追随者能量越低，其觅食位置越差，甚至会脱离种群。其位置更新描述见式4：

其中，yp是当前时刻种群中最优位置，yworse是种群中最差位置。A+=ATAAT－1。其中，A表示一个元素随机赋值为1或－1的1×d的矩阵。当i>n/2时，这表明第i个加入者无法获取食物，它可能会脱离种群，飞往其他地方觅食。

（5）反捕食行为。在麻雀种群中，随机生成所有麻雀初始位置，假定有小部分麻雀会意识到风险，并快速向周围同伴靠拢，降低自身被捕食的风险。其公式如下：

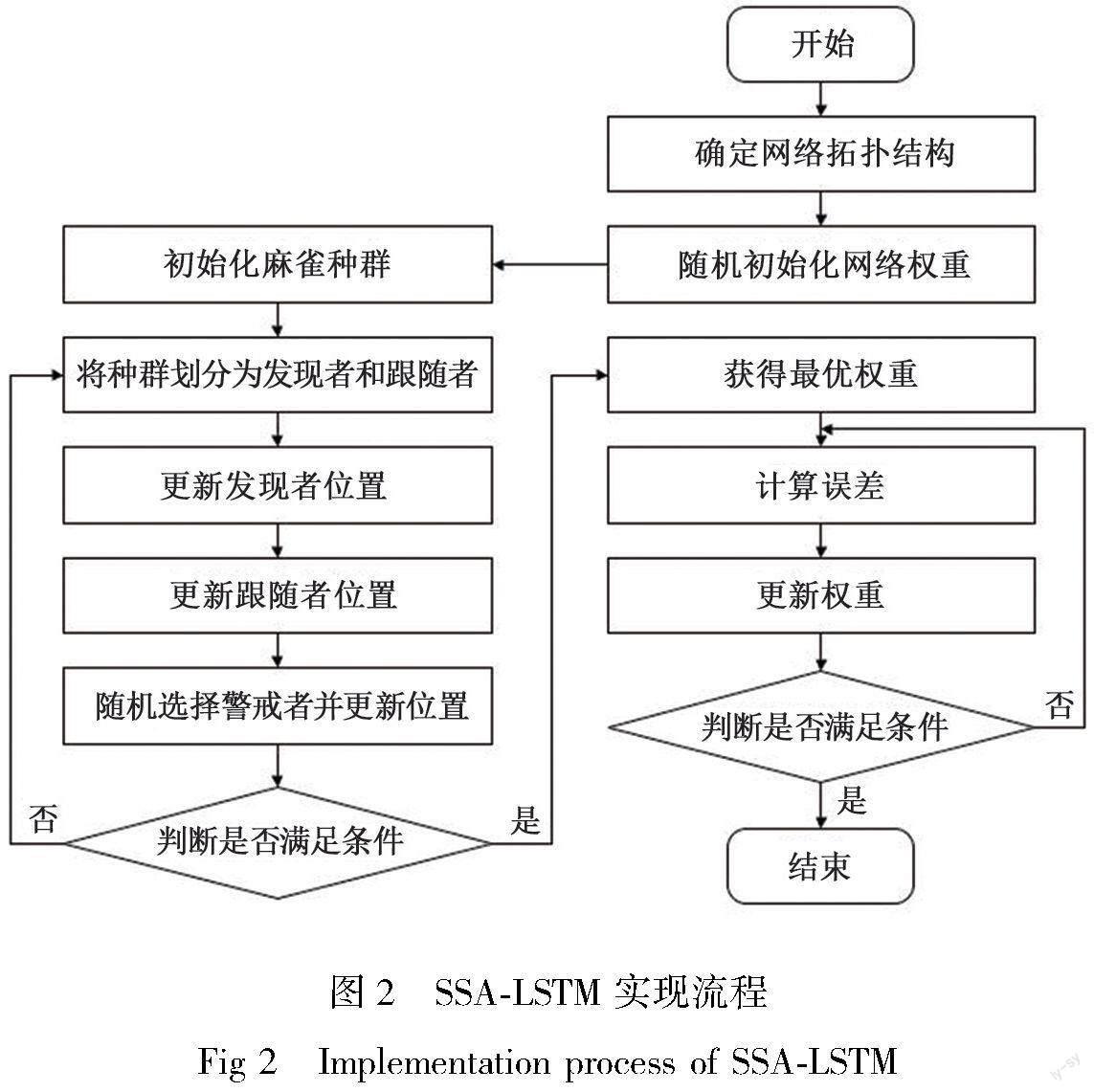
其中，ztbest是t时刻下最优解；z为x或y；fi为适应度值；当fi>fg，表明种群边缘的麻雀意识到风险；zbest代表种群中心位置，并且在其周围就是安全的；fi

用于控制步长，ε为非零小数，防止分母为零。

1.2 长短期记忆网络

为优化循环神经网络容易出现梯度消失等问题，研究学者提出长短期记忆网络（LSTM），通过引入“门”的概念，使得网络可以有选择性保留和遗忘信息[7]，从而使得LSTM网络更加高效。LSTM模型核心在于遗忘门、输入门、输出门和状态更新，其原理结构如图1所示。

（1）遗忘门。决定上一时刻细胞状态Ct－1有多少保留到当前时刻细胞状态Ct，通过激活函数决定。[JP]

其中，Wf，bf分别表示遗忘门的权重和偏差。［ht－1，xt］表示上一时刻隐藏状态和当前时刻输入的拼接。

（2）输入门。决定当前时刻输入xt有多少保存在当前时刻细胞状态Ct，同时通过tanh函数生成候选细胞状态。

其中，Wi，bi分别表示输入门的权重和偏差。

（3）输出门。决定与通过tanh层细胞状态逐对点乘的原始输出信息，最终得到模型输出。

其中，Wo，bo分别表示输出门的权重和偏差。

（4）状态更新。包括细胞状态Ct和隐藏状态ht更新。

1.3 SSA-LSTM组合模型实现流程

本文设计的基于SSA-LSTM组合模型的城市轨道交通客流短时预测流程见图2。

2 数据描述及预处理

2.1 数据描述

以杭州市轨道交通一号线2019年1月2—25日每日6：00—23：00的AFC进站刷卡数据为原始数据，其平均每日进站刷卡数据量为62.9万条，每条刷卡数据包括用户ID、刷卡时间、线路ID、车站ID、進出站状态以及支付类型等。通过逻辑判断和观察数据是否缺失对原始数据进行清洗，对数据进行5、10和15 min重采样作为研究对象。

考虑到模型的泛用性，选取的轨道交通站点数据应具有代表性。本文选取杭州地铁一号线有代表性的4个站点，分别是湘湖站（首发站）、城站（2019年1月为普通站）、近江站（普通换乘站）和火车东站（大型换乘站）作为研究对象（如图3所示），验证分析建立模型的可用性和有效性。

2.2 影响因素选取

对未来客流量进行预测，首先要明确客流量的影响因素。本文选取5 min前客流、[JP]10 min前客流量、15 min前客流量、空气污染指数（air quality index ，AQI）、天气状况、是否为节假日作为影响因素备选集，并利用皮尔逊相关性分析确定不同因素对客流量影响的相关程度，见式13。

根据表 1可知，每个时刻客流量与历史客流量的相关系数在90%左右，p值均小于0.01。由于当前时刻前5 min粒度的客流量与当前时刻客流量相关系数最高，因此，本文结合AQI与5 min粒度客流量对下一个5 min粒度客流量进行短时客流预测[8]，本文中AQI量化参数如表2所示。

2.3 经验模态分解降噪

经验模态分解是一种信号自适应并适用于非线性非平稳时间序列的处理方法[9]。由于轨道交通客流量具有非线性、非平稳特点，其存在一些高频噪声，可以通过经验模态分解将其分为有限个本征模函数（intrinsic mode function，IMF），所分解出来的各个IMF分量包含原始客流量全部特征，剔除其中高频噪声信号，从而更好地探究客流变化内在规律[10-11]。本文以一号线湘湖站为例，进行经验模态分解降噪处理。湘湖站2019年1月24日原始客流量可以分解为9个IMF分量和1个残差趋势项，IMF1至IMF9，频率依次降低，结果如图4所示。

实践表明，经验模态分解中信号噪声主要集中在高频部分，代表某些突发或不稳定客流量，直接带入模型会降低模型预测精度，低频部分为信号主要成分，代表稳定、相对固定的客流量，适合探究客流变化规律。为防止剔除高频噪声导致原始信号中包含的信息大量缺失，采用皮尔逊相关系数对原始数据和降噪后数据进行对比，得到相关系数为0.968，p值为0，可以确定降噪后客流数据保留的信息非常完整，对客流预测结果影响很小，如图5所示。

3 结果分析

3.1 模型运行

本文所建立模型程序运行环境为python3.6+tensorflow2.4.0+keras2.4.3，模型运行所构建的主要流程包括：

（1）经验模态分解（empirical mode decomposition，EMD）。消除一部分原始数据中高频噪声，防止模型过拟合以及干扰模型训练。

（2）SSA参数寻优。利用SSA算法对LSTM模型进行迭代，对模型参数进行寻优，从而避免盲目选取参数，可以有效提高模型精度。

（3）基于LSTM模型预测。使用步骤（1）处理过的时间序列，结合量化后AQI指标，分别重构为不同步长的序列数据组合作为模型的输入，将其代入模型进行多输入单输出短时客流预测。

本文构建的短时客流预测模型（SPFF）为3层结构[12]，如图6所示。模型包括一个LSTM层、两个全连接Dense层，为防止过拟合问题，添加Dropout层，“？”代表隐藏层神经元个数，由优化算法确定。

设置SSA算法中超参数包括种群数量为6，最大迭代次数为3，发现者在种群中比例为20%。为了研究模型的收敛速度，LSTM模型中epoch设置为3，批量大小为256，训练集和测试集比例为8：2，优化器采用Adam，损失函数为MSE损失函数。

3.2 模型评价指标

为使评价模型预测结果更加客观，本文采用均方根误差（δRMSE）和决定系数（R2）对模型进行评价。δRMSE反映预测值与真实值的差值，均方根误差越小，说明预测效果越好，R2反映预测结果对于真实值的拟合程度，通常来说，R2越接近1，拟合效果越好。

3.3 模型结果分析

为对比分析SSA-LSTM模型的有效性和精准度，选取LSTM模型、GA-LSTM模型和PSO-LSTM模型为对比模型。为保证模型可比性，各算法中LSTM部分网络拓扑结构、优化器等均保持一致。各模型的客流预测结果如图 7所示。

为了更直观观察不同模型以及不同时间步长对于模型精度影响，将预测结果进行反归一化后，与真实客流量进行对比，各个模型以及不同步长预测精度汇总如表 3所示。

由表3可知，在相同模型方法中，步长为1时，其拟合效果最差，步长为10时，拟合效果最优。LSTM模型平均均方根误差为33.72、平均R2为0.831，GA-LSTM模型平均均方根误差为26.54、平均R2为0.902，PSO-LSTM模型平均均方根误差为16.35、平均R2为0.966，SSA-LSTM模型平均均方根误差为8.56，平均R2为0.989。由此可见，单一LSTM模型预测效果最差，SSA-LSTM模型拟合效果最优，GA-LSTM和PSO-LSTM模型拟合效果次之。相比于LSTM、GA-LSTM和PSO-LSTM预测结果，本文所建立的SSA-LSTM的平均均方根误差分别减少了25.16、17.97和7.78，平均R2分别提高了19.1%、9.7%和2.4%。

4 结论

针对城市轨道交通短时客流规律性较差、非线性特征显著等特点，本文结合SSA学习能力强和收敛速度快的优势，建立了城市轨道交通短时客流预测的SSA-LSTM组合模型。利用杭州城市轨道交通1号线客流数据进行了模型的有效性和精確度验证。分析结果表明，相比于LSTM模型、GA-LSTM模型和PSO-LSTM模型，SSA-LSTM模型预测结果具有更低的RMSE值和更高的R2值，证实了SSA-LSTM组合模型在城市轨道交通客流预测中具有一定的应用价值，具有协助运营管理者提高城市轨道交通运营管理效益和提高服务水平的潜力。根据本文模型结果显示，当步长为10时预测效果最好，但其是否可能存在更优步长有待进一步挖掘。与此同时，后续可对不同类别轨道交通站点客流影响因素及特征进行深入探究分析，优化更多模型参数和网络结构，建立更高效、更精准且适用性更强的城市轨道交通短时客流预测模型。

参考文献：

［1］施雪蓉， 王宠惠， 刘东杰， 等. 基于深度神经网络的轨道交通客流预测及可视化[J]. 电子技术与软件工程， 2020（19）： 182-185.

[2]吕秋霞， 钟晓情， 任雅思. 基于Bi-LSTM网络的广珠城际短期客流预测方法[J]. 五邑大学学报（自然科学版）， 2022，36（1）： 50-56. DOI： 10.3969/j.issn.1006-7302.2022.01.007.

[3]赵明伟， 张文胜. 基于IPSO-LSTM组合模型的城市轨道交通短时客流预测[J]. 铁道运输与经济， 2022， 44（2）： 123-130. DOI： 10.16668/j.cnki.issn.1003-1421.2022.02.19.

[4]HALYAL S. Forecasting public transit passenger demand： With neural networks using APC data[J]. Case Studies on Transport Policy， 2022， 10（2）： 965-975. DOI： 10.1016/j.cstp.2022.03.011.

[5]GUO J Y， XIE Z， QIN Y， et al. Short-term abnormal passenger flow prediction based on the fusion of SVR and LSTM[J]. IEEE Access， 2019， 7： 42946-42955. DOI： 10.1109/ACCESS.2019.2907739.

[6]赵婧宇， 池越， 周亚同. 基于SSA-LSTM模型的短期电力负荷预测[J]. 电工电能新技术， 2022， 41（6）： 71-79. DOI： 10.12067/ATEEE2107053.

[7]吴娟， 何跃齐， 张宁， 等. 基于VMD-GRU的城市轨道交通短时客流预测[J]. 都市快轨交通， 2022， 35（1）： 79-86. DOI： 10.3969/j.issn.1672-6073.2022.01.013.

[8]马超群， 李培坤， 朱才华， 等. 基于不同时间粒度的城市轨道交通短时客流预测[J]. 长安大学学报（自然科学版）， 2020， 40（3）： 75-83. DOI： 10.19721/j.cnki.1671-8879.2020.03.008.

[9]何九冉， 四兵锋. EMD-RBF组合模型在城市轨道交通客流预测中的应用[J]. 铁道运输与经济， 2014， 36（10）： 87-92. DOI： 10.3969/j.issn.1003-1421.2014.10.017.

[10]朱才华， 孙晓黎， 李培坤， 等. 融合车站分类和数据降噪的城市轨道交通短时客流预测[J]. 铁道科学与工程学报， 2022， 19（8）： 2182-2192. DOI： 10.19713/j.cnki.43-1423/u.t20211018.

[11]谢鑫鑫. 基于EMD-KNN的城市轨道站点客流预测方法研究[D]. 苏州：苏州科技大学， 2021.

[12]张惠臻， 高正凯， 李建强， 等. 基于循环神经网络的城市轨道交通短时客流预测[J]. 吉林大学学报（工学版）， 2023， 53（2）： 430-438. DOI： 10.13229/j.cnki.jdxbgxb.20210720.