基于“撞硬墙”和“撞软墙”相结合的高速铁路列控系统控车方法研究

李微 张守帅

摘要：压缩列车追踪间隔可以显著提升行车密度，优化列控系统的控车方法是压缩追踪间隔的重要手段。目前常见的“撞硬墙”控车模式在效率上存在很大冗余，“撞软墙”控车模式又无法保证行车的绝对安全。因此提出“撞硬墙”和“撞软墙”相结合的控车模式，在保证列车绝对安全的前提下压缩列车追踪距离。给出了对该控车模式优化的基本原则，并针对该模式下前车速度无法获取、控车曲线无法满足约束的问题，探讨了基于轨道电路信息的列车速度估算方法和满足相关约束的控车曲线生成技术。以CRH380BL列车为例，编制求解程序获取了优化后的列控减速度建议取值，新控车模式下平直道上列车追踪距离可压缩3 035 m，区间追踪间隔时间可压缩31 s。这对提升高铁运营效率和线路通过能力有重要意义。

关键词：高速铁路；列控系统；撞软墙；撞硬墙；控车曲线；减速度

中图分类号：U283.1   文献标志码：A   文章编号：1002-4026（2023）05-0085-08

Train control method for high-speed railways combining“hit-hard-wall” and “hit-soft-wall” control modes

LI Wei1，ZHANG Shoushuai2

（1. Chengdu Institute of Rail Technology， Chengdu 610081，China；2. School of Transportation and Logistics，Southwest Jiaotong University， Chengdu 611756，China）

Abstract∶The passing capacity of several busy high-speed railway lines in China is declining， and reducing train headway can considerably improve train density.However， optimizing the control method for train control systems is important to reduce the headway. On one hand， the commonly employed “hit-hard-wall” control mode has redundancies， rendering it inefficient. On the other hand，the “hit-soft-wall” control mode cannot ensure the absolute safety of train operation. Therefore， this paper proposes a combined“hit-hard-wall” and “hit-soft-wall” control mode， which reduces train tracking interval while ensuring the absolute safety of the train. Further， basic principles for optimizing this control mode are presented herein.In addition， solutions for problems such as the inability to determine the speed of the preceding train and to fulfill control curve constraints under this mode are explored.The solutions include track circuit information-based train speed estimation and control curve generation techniques that satisfy relevant constraints. Considering the CRH380BL train as an example， a solution was developed to obtain recommended values for train control deceleration.Consequently， the train tracking interval on straight tracks was reduced by 3035 meters， and the interval tracking time was reduced by 31 seconds through the proposed control mode. This is of great significance for improving the operational efficiency and passing capacity of high-speed  railway lines.

Key words∶high-speed railway; train control system; hit-soft-wall; hit-hard-wall; train control curve; deceleration

我國高速铁路发展迅速，截至2021年底，我国高速铁路运营里程超4万公里，2019年动车组客运量达22.9亿人次，占铁路总客流的62.6%以上[1-2]。随着人民生活水平的提升以及高铁路网规模效应的逐步体现，高速铁路客流量将不断增加，部分高铁繁忙区段的能力接近饱和，如京沪高铁徐蚌段开行列车154对[3]，沪杭高铁开行列车162.5对[4]，理论计算的通过能力利用率已经超过100%，相对受限的线路能力与日益增长的客运需求之间的矛盾日益突出，对提升线路通过能力的需求日益迫切。

高铁通过能力主要取决于追踪间隔时间以及运输组织模式（列车速度等级、停站方式等）[5]。列车追踪间隔时间是线路、车辆、信号、运营等各专业综合水平的最终体现，通过压缩列车追踪间隔时间可以显著提升线路的通过能力[6]。

国内外学者对追踪间隔时间压缩方法进行了大量的研究探索[7-8]，并提出了优化行车组织方式，改变咽喉布置，优化闭塞方式，优化控车曲线等方法，在实践中取得了明显的成效，如日本东海道新干线、法国的北方线，以及我国的沪杭高铁等300 km/h及以上的线路上均实现了3 min追踪[9-11]。但整体来看，对既有线路或动车组进行改造周期长、成本大，相比之下优化高铁列车的控车模式是缩小追踪间隔时间、提高行车密度的关键。

1 高铁控车方法分析

1.1 “撞硬墙”的列车追踪模式

目前国内外列控系统普遍基于“撞硬墙”的追踪模式来进行设计，具体的控车算法（即车载监控制动距离的计算方法）又分为欧标法和日立法两大类[12]。“撞硬墙”的追踪模式是考虑到前方列车可能存在立刻停止的情况（如脱轨、发生冲撞等），因此后车的追踪终点为前车所在闭塞分区入口并附加一定的安全防护距离。前后列车之间保持一个车载监控制动距离，随时确保后车可在前车所在闭塞分区的入口停车以保证安全。

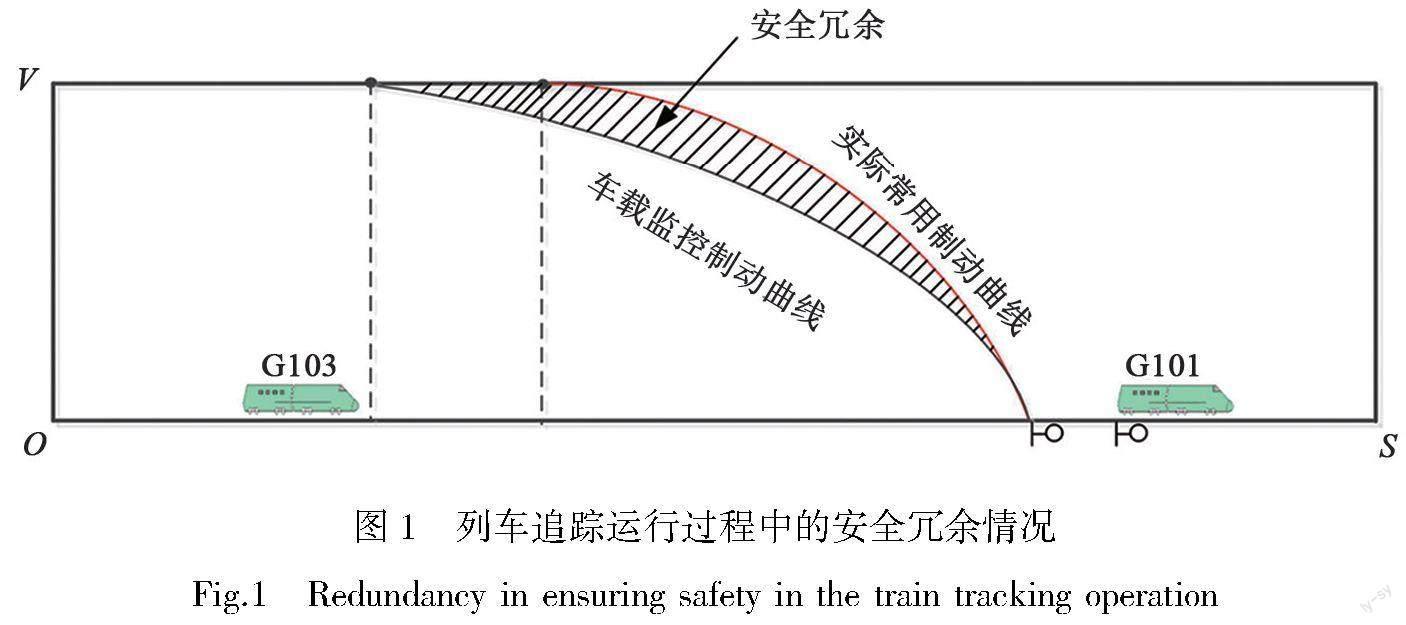
列控系统的车载监控制动距离是根据动车组的制动性能、坡度等参数计算得出，并考虑到计算机的可靠性、实时性等对计算方法进行了大量简化，因此车载监控制动距离大于动车组实际制动距离，这导致前后两车之间的间距存在较大安全冗余（如图1所示），限制了运营效率的提高。

1.2 “撞软墙”的列车追踪模式

随着列车运行速度的提高，采用“撞硬墙”的控车模式计算出的车载监控制动距离越来越大，因此追踪间隔时间越来越大。为了解决这一问题，学者提出了“撞软墙”的列车追踪运行模式[13]。

“撞软墙”的列车追踪模式，即假设前车不会发生脱轨或冲撞导致在很短的距离内停车的前提下，前行列车采用紧急制动停车后，后行列车可以采用常用制动在前行列车尾部停车，如图2所示。此时，两车之间的追踪间隔相比“撞硬墙”模式，会压缩一个前车的紧急制动距离，进而大大提高了行车密度。

目前相关学者提出涉及“撞软墙”的具体理论和方法主要是针对城市轨道交通，但该方法很难在高速铁路上应用，这主要有两方面的问题：

一是“撞软墙”模式下，后车需要掌握前车的速度、位置、状态（载重、制动能力）、线路条件等信息，这涉及到车与车之间的通信。但高速铁路主要依靠地面应答器、轨道电路等实现列车定位和完整性检查，同时考虑到铁路网上不同速度等级和种类的列车跨线运行带来的复杂性，短期内很难实现“车-车通信”，也就失去了采用“撞软墙”模式的技术基础[14]。

二是“撞软墙”模式下，需要确保前行列车不会出现原地脱轨的情形，即最不利情况下前行列车也将继续运行一个紧急制动距离，否则后行列车将与前行列车发生追尾。高速铁路运行环境恶劣，无法避免各类外界因素导致线路中断、列车脱轨的风险。

整体来看，“撞硬墙”控车模式下车载监控制动距离含有较大冗余，增大了追踪间隔时间，限制了行车密度的进一步提升。“撞软墙”控车模式的前提是具备“车-车通信”功能，且在前车不会发生脱轨或冲撞等情况的假设下才能实现，且该控车模式无法保证后车的绝对安全，与目前铁路运营安全理念相悖，也没有在实际当中具体实现。

为了能够进一步压缩追踪间隔时间，同时保证在各场景下的适应性与安全性，本文提出了“撞硬墙”和“撞软墙”相结合的追踪模式。

2 “撞硬墙”和“撞软墙”相结合的追踪模式

由于“撞硬墙”的追踪模式存在一定的安全冗余，但该模式下安全性可以得到保障，而“撞软墙”的追踪模式可以实现压缩追踪间隔进而提高通过能力，但该模式下安全性不能得到保障，因此本文根据两种追踪模式各自的特点，提出了一种“撞软墙”模式和“撞硬墙”模式相结合的追踪模式，如图3所示，其中G103为目前“撞硬墙”模式下的后车位置，G103′为本文提出的新控车模式下的后车位置。

该控车模式的主要原则为：

（1）确保列车运行的绝对安全，从紧急制动的层面确保仍为“撞硬墙”，即在任意情况下后行列车采用紧急制动后，其都不应超过前车当前位置，如图3中G103距离G101尾部（或所在闭塞分区入口）至少为1个紧急制动距离。

（2）为列车追踪留有一定冗余，避免后行列车频繁进入紧急制动。由于列车进入紧急制动后只有完全停车后才能缓解，因此除了要求后车距离前车一个紧急制动距离（S3～S4）外，还应留有一定冗余（S2～S3），保证在前行列车略有降速等情况下，后行列车可先进入常用制动，当前车恢复高速运行后，后车也可正常恢复运行。

（3）充分借鉴“撞软墙”的理念，进一步提升行车效率，即后行列车无需在距离前车尾部（S4）一个车载监控制动距离的位置（S1），而是考虑到绝大多数情况下前行列车都不会突然停止，即便发生突发情况，前行列车采取緊急制动，也将继续向前运行一个紧急制动距离（S5～S7），因此后车的常用制动曲线可由前车紧急制动停车后的车尾位置（S6）开始推算得出（S2），这不仅要求优化后的列车可实现更紧密的追踪（S2～S4的距离要小于S1～S4的距离），且推算出的常用制动点S2在紧急制动点S3之前并留有一定冗余。

（4）列车运行过程中由于抵消位置、速度的测量误差需要在前行列车的尾部（或所在闭塞分区入口）设置一定的安全防护距离，以及地面和车载信号设备反应时间以及信号传输时间等，都需要留够充足的冗余，由于无论是距离还是时间一般都当一个固定值来考虑，因此本研究暂不考虑该部分影响。

3 控车曲线生成方法研究

若要实现“撞硬墙”与“撞软墙”相结合的控车方法，需解决两个关键问题：

（1）由于高速铁路尚未实现“车-车通信”，因此后行列车如何掌握前行列车的运行速度，进而计算得出前车的紧急制动距离亟待解决。

（2）目前高速列车的车载监控制动距离虽然具有较大冗余，但相较于两倍的紧急制动距离而言较小，若直接应用于本控车模式，则会导致后行列车先触碰到紧急制动曲线，不满足上文提出的“常用制动点在紧急制动点之前且留有一定冗余”的要求。

3.1 现有技术条件下前行列车速度的推算方法

由于目前我国高速铁路CTCS-3级列控系统实现了“车-地通信”，后行列车可通过GSM-R获得前方32 km范围内的线路条件，通过轨道电路占用情况获得前方列车的大致位置，但是无法获得前行列车的速度信息，也就无法推断出前行列车的紧急制动距离。本文提出一种前行列车运行速度的估算方法。若后续通过相关技术手段使得前车速度可获取时，可采用实际获得的前车速度值替换本方法估算出的速度值。

根据估算得出的前行列车速度，可结合线路条件计算得到紧急制动距离，该紧急制动距离存在一定的误差。当估算的前行列车紧急制动距离短于实际紧急制动距离时，列车追踪将具有额外冗余，即便前车紧急制动，后车也完全可以采用常用制动停车；反之，当估算的前行列车紧急制动距离长于实际紧急制动距离时，后行列车常用制动的打靶点将过于靠前，导致两列车距离过近，一旦前车出现紧急制动的情况，无法保证后车仅依靠常用制动即可停车。因此，为了避免后车出现紧急制动的情况，有必要在估算前行列车速度时按照较不利的情况估算。

后行列车估算前行列车速度的主要依据是前一轨道电路占用和出清时机。当前列车在轨道电路上由占用状态变为空闲状态时，前行列车共走行了一个闭塞分区长度Lb外加一列车长度Lt，走行时间为该轨道电路状态从开始占用到结束占用的时间Δtc。

由于需按照最不利场景考虑以确保前后车的绝对安全，因此假定前车正处于制动过程中，制动减速度a可根据动车组性能获得，制动安全距离满足公式：

显然，该方法是对前车在不利场景下制动距离的估算，估算所采用的制动初速度要低于实际制动初速度，一般情况下计算出的前车紧急停车点也要短于实际制动距离，对后车而言多了一部分安全冗余。

此外，只有当前车出清一个闭塞分区时，轨道电路占用状态才变化一次，前车紧急制动点也才更新一次，减少了车载计算机的计算复杂度。

3.2 车载监控制动距离的优化方法

CRH380BL动车组以350 km/h初速度在平直道运行时，其紧急制动距离为6 038 m，目前的车载监控制动距离为11 425 m，也就意味着如果不改变控车曲线算法的情况下，采用“撞硬墙”与“撞软墙”相结合的模式，后车在运行时会首先进入紧急制动，而这违背了该模式的设计初衷，因此有必要对车载监控制动距离的计算方法进行调整。

目前列控系统的车载减速度取值一般是分为六段，车载计算机根据该减速度取值来计算制動距离并生成控车曲线。调整车载监控制动距离的关键在于优化制动减速度取值[15]。

由于调整后的控车曲线需要在不同速度、不同坡度下均满足本文提出该控车模式的4项原则，因此针对每个减速度取值方案均需进行坡度、速度的双重检测。本文采用遍历法对减速度取值进行尝试，并结合经验优化了检索顺序，提出控车曲线的优化算法如下：

步骤1 计算出“撞硬墙”情况下前后两车不同速度等级下（如以10 km/h为间隔）的紧急制动距离（S3～S4、S5～S6），并以前车尾部为起点采用现有的控车算法推算后车常用制动距离（S1～S4），以下用Lfe、Lbe、Lbs来表示。

紧急制动距离Le应当包括列车进入紧急制动初期制动力未完全施加的制动空走时间tea，在该时间内列车仍按正常速度vp运行；列车从最高速度vp制动到完全停车即速度为0的距离，该过程中列车受到制动力Fe、基本阻力Fb、附加阻力Fa的影响，其中Fe一般以制动减速度ae的形式体现，Fb一般由基本阻力公式计算得出，Fa一般根据线路条件如坡度和曲线综合确定。

常用制动距离Ls应当包括列车的空走距离vp·tsa，以及列车按常用制动减速度从最高速度制动到0速的距离，该过程取决于列控系统中存储的制动减速度。

步骤2 计算出“撞软墙”情况下的前后车追踪距离Lf，

步骤3 检查是否符合相关约束。

（1）当前列车减速影响后车运行时，后车应首先采用常用制动，经过一定的安全冗余时间tr后才能进入紧急制动。

（2）采用新控车模式后的追踪距离要小于目前“撞硬墙”模式下的追踪距离。

步骤4 约束无法满足时的相关措施。首先选定一个典型坡度（以5‰为单位从-20‰～20‰确定典型坡度），调整目前的控车参数（即列控系统中减速度的取值），自低到高对比各速度间隔下是否满足相关约束，若不满足相关约束，则将该速度等级下的减速度取值向下调整0.01 m/s2，并按照新的参数重新返回步骤1进行计算，直至所有的约束均得到满足，之后选择未计算过的坡度再次重复上面的计算过程，最终得到一个满足所有速度等级、所有坡度下的减速度取值，此时的减速度取值即为优化后控车曲线的减速度取值依据，其步骤见图4。

4 新型控车模式下列车追踪间隔时间的压缩效果分析

本文以CRH380BL动车组装备CTCS3-300T列控系统为例，分析其采用现有模式以及采用优化后模式的列车追踪距离、列车间隔时间，以验证本研究的有效性。

CRH380BL动车组基本参数见表1[16]。

该算例在AMD Ryzen 7 PRO 5850U，1.90 GHz，16GB RAM的计算机上完成，并通过Python3.9编程采用前述遍历算法实现求解，求解时间在1 s以内。

列控系统减速度由当前减速度逐渐优化至满足约束要求减速度的过程如图5所示。

由图5可见，减速度的优化过程是按照算法设计的由低到高速度区间的过程进行逐步调整的，其中280～350 km/h段的优化结果随着列车最高速度的增加而不断变化，其他各段则在275 km/h及以上的范围内取值基本不变。

列控系统制动减速度优化后的取值情况如表4所示。

优化前该列车在平直道的车载监控制动距离为10 537 m，对应区间追踪间隔时间为134 s；优化后的车载监控制动距离为14 621 m，紧急制动距离为7 119 m，两列车的追踪距离为7 502 m，对应区间追踪间隔时间为103 s。可见该追踪模式下列车的追踪距离压缩了3 035 m，区间追踪间隔时间压缩了31 s，同时确保了列车不会触发紧急制动。

5 结论

本文提出了基于“撞硬墙”和“撞软墙”相结合的新型高速铁路控车模式，新型控车模式在确保紧急制动“撞硬墙”的安全前提下，对常用制动采取“撞软墙”的方式压缩了列车追踪距离。考虑到我国高铁设备暂不具备车车通信的条件，提出了基于轨道电路的前车运行速度预估方法和常用制动控车曲线的生成方法。最后以CRH380BL动车组装备CTCS3-300T列控系统为例，采用Python编程语言对列控系统减速度值进行优化，结果表明本研究提出的算法运算时间在1 s以内，优化后的控车曲线在确保列车追踪距离大于紧急制动距离的前提下，列车追踪间隔压缩了23%。因此，本研究提出的控车模式可显著提高线路通过能力。但本研究目前尚未涉及列车在有道岔区段的追踪方式，这限制了车站间隔时间的压缩，后续将对列车进出站场景进行探索，以期实现列车追踪间隔时间的全过程压缩。

参考文献：

［1］田长海. 发展中的我国铁路列车速度、密度、重量[J]. 中国铁道科学， 2020， 41（4）： 127-135. DOI： 10.3969/j.issn.1001-4632.2020.04.15.

[2]齐壮. 航空业竞争下中国高速铁路运营优化探讨[J]. 铁道运输与经济， 2021， 43（8）： 25-29. DOI： 10.16668/j.cnki.issn.1003-1421.2021.08.05.

[3]曲思源， 施俊泉， 徐瑞华. 京沪高铁开行时速350 km动车组列车通过能力评估分析[J]. 中国铁路， 2022（2）： 36-46. DOI： 10.19549/j.issn.1001-683x.2021.12.24.001.

[4]曲思源， 卢万胜. 沪杭高铁运营组织方案优化研究[J]. 交通运输工程与信息学报， 2016， 14（3）：31-37. DOI： 10.3969/j.issn.1672-4747.2016.03.006.

[5]邹信诚， 李海鹰， 廖正文， 等. 考虑服务水平的高速铁路通过能力利用研究[J]. 铁道科学与工程学报， 2022， 19（11）： 3127-3137. DOI： 10.19713/j.cnki.43-1423/u.t20220067.

[6]趙欣苗， 尹相勇， 李茜，等. 列车追踪间隔时间对高速铁路通过能力利用的影响分析[J]. 铁道科学与工程学报， 2016， 13（11）： 2099-2106. DOI：10.19713/j.cnki.43-1423/u.2016.11.001.

[7]鲁工圆， 王超宇， 沈子力， 等. 面向追踪间隔压缩的高速铁路列车运行时空轨迹优化[J]. 铁道学报， 2021， 43（7）： 10-18. DOI： 10.3969/j.issn.1001-8360.2021.07.002.

[8]EMERY D. Enhanced ETCS_L2/L3 train control system[M]//AdvancedTrainControlSystems.Billerica，MA ：WITPress， 2010： 113-122. DOI： 10.2495/978-1-84564-494-9/13.

[9]张守帅， 李微， 卢万胜， 等. 沪杭高速铁路列车间隔时间取值计算与试验分析[J]. 铁道运输与经济， 2021， 43（10）： 1-7. DOI： 10.16668/j.cnki.issn.1003-1421.2021.10.01.

[10]方琪根， 邢二平， 李竹君， 等. 我国与日本高速铁路通过能力参数的比较研究[J]. 中国铁路， 2016（10）： 53-56. DOI： 10.19549/j.issn.1001-683x.2016.10.013.

[11]安迪. 时速400 km高速铁路列车追踪间隔仿真研究[J]. 铁道运输与经济， 2022， 44（8）： 36-44. DOI： 10.16668/j.cnki.issn.1003-1421.2022.08.06.

[12]卫和君. 高铁车载ATP制动控车模式曲线计算方法的研究[J]. 铁路通信信号工程技术， 2013， 10（S1）： 33-38.

[13]董海霞. 面向高密度追踪的新型列控系统行车许可生成方法研究[D]. 北京： 北京交通大学， 2021.

[14]宁滨， 莫志松， 李开成. 高速铁路信号系统智能技术应用及发展[J]. 铁道学报， 2019， 41（3）： 1-9. DOI： 10.3969/j.issn.1001-8360.2019.03.001.

[15]张守帅， 田长海. 高速铁路长大下坡地段列车运行速度相关问题研究[J]. 中国铁道科学， 2017， 38（3）： 124-129. DOI： 10.3969/j.issn.1001-4632.2017.03.18.

[16]国家铁路局. 列车牵引计算：第1部分机车牵引式列车：TB/T 1407.1—2018[S]. 北京：中国铁道出版社，2018.