基于母题情境的习题变式教学初探——以匀变速直线运动中位移的求解为例

李 伟

(福建省宁化第一中学,福建 三明 365400)

习题教学是物理教学中的重要组成部分,它可以帮助学生理解物理概念、掌握物理定律等,不仅如此,习题教学在拓展学生思维能力、培养学生学科素养上也有举足轻重的作用.一种行之有效的习题教学模式是基于母题情境,设置系列问题串进行习题变式,从而达到巩固所学知识、发展思维能力的作用.

1 基于母题情境的习题变式概述

基于母题情境的习题变式,一般是指在全部保留或部分保留母题中的情境前提下,通过改变已知条件从而变换成新的问题,新问题既保留有母题中某些共性部分,又对母题中的相关条件做更改.通常来讲,这种变式往往在学生学习完某一物理规律后,为帮助学生理解规律、掌握规律进而运用规律解决问题而展开的一种当前较为流行的教学模式[1].

2 习题变式教学的优点

2.1 习题变式教学有利于学生对物理概念、物理定理、物理定律的掌握

物理学是研究物质结构及其相互作用规律的学科,学习物理离不开对基本概念、基本定理和物理定律的理解和运用,习题教学往往能较好地帮助学生去理解规律、巩固定理定律,进而运用物理规律解决问题.相比之下,基于某一母题提供的情境,不断变化题设条件,将问题向纵深方向引导,有利于学生将要解决的问题所必备的物理知识进行系统化、系列化,形成个人的知识体系.此为习题变式教学的最基础的功能[2].

2.2 习题变式教学有利于提高学生从不同的视角解决物理问题的能力

物理学科的学习真正的意义并不在于掌握了多少物理知识,记住了多少公式,理解了多少定理定律,终极目的是通过对物理学科的学习培养出能在实际生产生活中解决问题的能力,即学以致用.习题变式教学基于母题情境,变化已知条件,形成问题链,必然要求学生在储备了足够多的物理知识基础上,具备多角度解决问题的能力,显然,习题变式教学有利于提高学生从不同的视角解决物理问题的能力.

2.3 习题变式教学有利于培养学生的发散性思维

习题变式教学本质是一题多变,集中体现为发散性思维能力,发散性思维要求从某一点出发,向纵深角度不断地拓展延伸,只有具备了这一发散性思维,才有可能解决好形成的系列物理问题,从这个角度看,习题变式教学对培养学生的发散性思维起到了举足轻重的作用[3].

2.4 习题变式教学有利于提高学生的物理学科素养

2017版的普通高中课程标准,提出以全面培养学生的“学科核心素养”为育人目标的新理念.高中物理习题变式教学在学生学习掌握最基本的物理学知识基础上,多角度认识问题、分析问题进而解决问题,通过系列问题的不断探究,培养学生优秀的科学素养和严谨的不断进取的科学态度,从而形成从物理学视角看待、认清问题本质的正确的物理观念[4].

3 匀变速直线运动位移求解方法概述

速度、时间、位移和加速度等核心概念是描述运动的重要物理量,在匀变速直线运动的众多规律中都或多或少与运动的位移有关,因而在分析求解匀变速直线运动的众多问题中,分析探讨位移的系列解法显得尤为必要,这里梳理出匀变速直线运动位移的几种典型求法,以便在后述问题变式中围绕此类典型解法设计问题的变式[5].

4 匀变速直线运动位移问题的变式设计

母题:一辆汽车在平直的公路上做加速度为1 m/s2的匀加速直线运动,某时刻其速度为10 m/s,求汽车在接下来的5 s内通过的位移?

4.1 变换已知条件,巩固位移速度规律

变式一一辆汽车在平直的公路上做加速度为1 m/s2的匀加速直线运动,某时刻其速度为10 m/s,经过一段时间后其速度变为15 m/s,求汽车在这一过程中通过的位移?

比较变式一和母题,在保持母题中基本运动情境和初速度、加速度等基本条件不变外,仅将时间t已知变换为末速度vt已知,问题的本质并没有变化,显然变式后的问题依然可以运用位移时间关系求解,只不过先要借助速度时间关系求出时间而已,当然如若变式的目的是运用速度位移关系解决问题,巩固运用位移速度关系解决问题,教师教学时便要进行恰当的暗示,引导学生运用更为简捷的关系式处理问题.

4.2 变换已知条件,巩固平均速度关系

变式二一辆汽车在平直的公路上做匀加速直线运动,某时刻其速度为10 m/s,5 s后其速度增加为15 m/s,求汽车在这一过程中通过的位移?

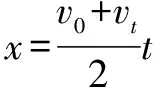
4.3 变换已知条件,巩固位移差关系式

做匀变速直线运动的位移,在相同的相邻时间T内发生的位移之差为一恒定值为Δx=aT2,如果问题涉及相同时间的位移问题,运用推论解题更快捷.故可以在母题的情境中,变换条件创设相同时间这一关键要素.

变式三一辆汽车在平直的公路上做匀加速直线运动,某时刻其速度为10 m/s,且第5 s内发生的位移比第1 s内多4 m,求汽车在这5 s内通过的位移?

变式三相比于母题,删除了加速度这一已知量,替之以第5 s内发生的位移比第1 s内多4 m这一条件,求解的问题保持不变,针对新添加的条件很容易想到运用位移差公式锁定出加速度这一量(x第5s内-x第1s内=4aT2),再结合位移时间关系求出5 s内的位移.

4.4 变换已知条件,巩固比例式规律

对于初速度为零的匀加速直线运动,可以从匀变速直线运动的基本关系式导出诸如1T末、2T末、3T末…的速度之比、第1个T内、第2个T内、第3个T内…的位移之比及1T内、2T内、3T内…的位移之比等比例式,根据母题中的基本情境,可以变换题中所给条件,运用比例式来解决问题.

变式四一辆汽车在平直的公路上从静止开始做匀加速直线运动,已知第1 s内发生的位移0.5 m,求汽车在5 s内通过的位移?

变式四与母题相比较,条件上有了较大的变化,运动情境也不完全相同,变式四汽车的初速度为零,这是运动情境的稍微变化,题给条件从母题中的初速度、加速度和时间则直接简化为第一秒内的位移,条件的变换幅度很大,通过分析变式四的问题情境和题给条件,很易分析出运用初速度为零的匀加速度直线运动的位移比1T内、2T内、3T内…nT内的位移之比等于12∶22∶32∶…∶n2解题方便.

4.5 变换已知条件,巩固图像面积意义

速度时间图像与横轴围成的图形面积表示物体在相应过程通过的位移大小,因而可以基于母题中的情境,通过变换条件来巩固图像意义.

变式五一辆汽车在平直的公路上做加速度为1 m/s2的匀加速直线运动,某时刻其速度为10 m/s,请画出相应图像并根据图像求解汽车在接下来的5 s内通过的位移?

变式五问题本身并不难,只要大体画出这一过程的速度时间图像,并根据图像的面积便可求出位移.当然,因匀变速直线运动加速度保持不变,其速度时间图像是一条倾斜的曲线如图1,纵截距为初速度,斜率为加速度,据此简单分析便可得5 s末速度为15 m/s,于是图像与横轴形成一梯形,求得梯形面积即可.

图1 用v-s图像面积求位移大小

上述五种变式中,全保留或部分保留了母题中的运动情境,通过对题给条件的多种变换,形成了对各类方法求解匀变速直线运动位移的系列求法.综上所述,只要加强分析研究,挖掘母题背景和条件,问题的变式都可不断地被开发应用于物理教学中,当然也不局限于匀变速直线运动的位移求解教学,在教学时要多思考、多研究,争取实现系列变换,为培养学生的学科素养而不懈努力.