级联触发策略下非结构化道路的自主卡车队列控制

岳 伟,吕 顺 ,刘中常 ,李莉莉 ,王丽媛 ,邹存名

(1.大连海事大学船舶电气工程学院,辽宁大连 116026;2.大连民族大学机电工程学院,辽宁大连 116600;3.辽宁警察学院公共安全管理系,辽宁大连 116036)

1 引言

近年来,随着国民经济的不断发展,对于矿区、码头、油田等非结构化道路区域的货物运输需求进一步增加[1].卡车作为非结构化道路上的主要运输工具,有装载量大、效率高、专用化等优点,在货物运输中起到了重要的作用.但是在经济效益显著提高的同时,也带来了驾驶安全、能源消耗等严峻的问题[2].自主卡车队列系统,通过以紧凑的队列形式行驶,可以有效减少空气阻力,降低车辆的能源消耗、提高道路安全性和通行能力.因此,针对非结构化道路上的卡车队列控制研究具有重要理论意义和实际应用价值.

车辆队列研究可追溯到20世纪90年代美国的PATH项目.随后其他国家也相继开展了相关研究.对于卡车队列的研究发展较晚,由于其特殊的多车体结构,以及复杂的执行机构,导致针对于自主卡车队列控制问题的研究更加困难.近年来国内外学者针对自主卡车队列的相关问题做出了大量的研究.

文献[3]最早建立了基于速度误差和距离误差的卡车纵向队列模型,并通过实验实现了车队在直线道路上的稳定运行,验证了模型的有效性,采用的模型将卡车作为一个刚体,没有充分考虑卡车的双车体结构,且在横向控制上均采用车道线跟随的方式,严重依赖于道路的结构化程度.目前,对于非结构化道路的自主卡车队列控制问题鲜有研究.

另一方面,自主卡车执行机构较为复杂,而且工作时间长、工作环境差,在实际的运行过程中,车辆自身机构损耗及外部干扰等问题会对车队造成严重影响.文献[4]对车队系统中存在的执行器故障、饱和等问题进行了详细研究.为了进一步提高车辆燃油经济性和舒适性,文献[5]利用事件触发方法研究有带有执行器和传感器故障的自主车队控制问题,通过事件触发方式减少传感器和控制器之间非必要信号的传输,从而减少执行器的频繁操作,提高了车辆的舒适性和燃油经济性.然而,尽管上述研究涉及了执行器故障、传感器故障和网络故障等问题,但针对自主卡车车队的研究的问题较为单一.

基于上述分析,本文重点研究了在非结构化弯曲道路上受到执行器故障、传感器故障和网络故障影响的卡车队列协同控制问题,提出了一种基于级联触发的控制方案.主要贡献概括为以下几个方面:

1) 考虑卡车特殊的双车体结构,根据车队中前后车之间的几何位置关系,建立了非结构化弯曲道路下卡车队列纵–横向耦合的队列模型.

2) 提出了基于自触发和事件触发的级联触发方案,通过减少传感器非必要信息的传输,进一步降低执行器的频繁操作,有效减低燃油消耗.

3) 针对车辆存在的执行器故障、传感器故障和网络故障问题,考虑级联触发方案,设计了基于级联触发的控制器.

2 问题描述

考虑n+1 辆卡车组成的自主卡车队列系统,包括1辆领航车和n辆跟随车,领航车编号为i=0,跟随车为i=1,2,···,n.利用V2V通信技术,系统中每辆跟随车都可以周期性的接收前车的位置、航向和速度信息,且所有跟随车都装有激光雷达传感器,可测量与前车辆的相对距离信息.

2.1 卡车运动学建模

卡车系统由牵引车和半挂车两个刚体组成,其中牵引车为后轮驱动、前轮转向,半挂车属于从动部分,其运动姿态可根据与牵引车的几何关系获取,图描述了在全球坐标系XOY下,第i辆卡车系统的结构示意图,在建立运动学模型前,做出如下假设:

1) 整个卡车系统在同一个平面上运动.

2) 卡车的两车体关于纵向轴线对称.

3) 两车体均做纯滚动运动,即不打滑.

4) 两车体无侧向滑动,即无横向运动.

则车队系统中第i辆卡车运动学模型[6]可表示为

其中: (xhi,yhi)和(xti,yti)分别为半挂车和牵引车的平面位置坐标,δi为牵引车前轮转角,θhi为牵引车航向角,lhi为牵引车轴距,vhi为牵引车速度;θti为半挂车航向角,lti为半挂车后轮轮轴到链接点的长度,vti为半挂车速度,且vti=vhicos(θhi-θti).

2.2 卡车队列建模

考虑非结构化弯曲道路上的第i辆与第i-1辆卡车之间的几何位置,如图1所示.根据卡车运动学模型(1),可描述两辆卡车的相对位置关系为

图1 相邻车辆相对位置示意图Fig.1 Relative position schematic

其中:Oh(i-1)(xh(i-1),yh(i-1))和Ohi(xhi,yhi)分别为第i辆和第i-1辆卡车的牵引车平面坐标;Ri是第i辆卡车的牵引车与第i-1辆卡车的半挂车之间的距离,αi是第i辆卡车的牵引车与第i-1辆卡车的半挂车之间的相对航向角,θt(i-1)表示第i-1辆卡车的半挂车航向角度.

根据式(1)–(2),建立非结构化弯曲道路上卡车队列模型如下:

其中:ai表示第i辆卡车的牵引车加速度,ϕi代表第i辆卡车的牵引车与第i-1辆卡车的半挂车之间的跟随角度,θh(i-1)表示第i-1辆卡车的牵引车航向角度,vh(i-1)和vt(i-1)分别表示第i-1辆卡车的牵引车速度和半挂车速度,且

注1本文所建立的卡车队列模型(3)为纵横向耦合,相比单纯的纵向队列模型具有更强的非线性特性和不确定性,为简单起见,本文考虑的是一个卡车队列中各车辆具有期望距离和期望跟随角度的问题,同时假设车队中所有车辆的期望车间距离以及期望跟随角度相同,具体表示为

2.3 模型线性化

本文将状态反馈控制用于车队的控制任务之中,但是需要状态变量都是可测的,对于模型(3),存在不可测的状态,如车辆的航向角度信息,因此难以直接设计有效的非线性控制器,需要对其进行线性化处理.考虑系统在某个平衡点附近可以平稳运行,则可采用文献[7]的方法,在系统的平衡点附近,对非线性车队模型(3)进行线性化处理.设卡车队列模型(3)的平衡点输入为

其中aeq和δeq分别表示车队在平衡状态下牵引车的加速度和前轮转向角度.

定义线性化后卡车队列系统中第i辆卡车的状态向量为

进而,建立平衡点(xeq,ueq)下的卡车队列线性化模型

其中:ui=[ai δi]T为控制输入,

为前车的状态向量,系数矩阵为

对于每一辆跟随车,设计控制器结构如下:

其中:

为待设计的控制器增益.

2.4 级联触发方案设计

由于卡车载荷重、牵引力大,采用传统的周期采样机制会使车辆的控制器频繁更新控制命令,执行器出现过多的加/减速操作,直接增加车辆的燃油消耗.为了减少卡车队列系统的能耗,本文构建基于自触发和事件触发的级联触发机制,如图2所示,其中自触发采样器,用来计算每辆卡车控制系统的下一个采样时刻.在每个自触发时刻设置事件触发条件,仅当满足此事件触发条件时,进行控制器状态的更新,从而有效减少控制器的更新频率,降低油耗.

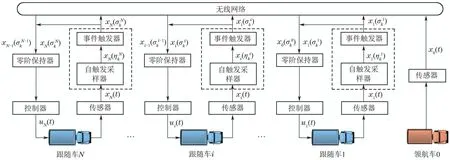
图2 卡车队列系统级联触发控制框架Fig.2 Cascade-trigger control framework

对第i辆卡车的级联触发条件设计为

其中:λi(xi(t),xi())为自适应参数的调节函数,设计为

其中:arctan(·)是反正切函数,0<µi<1 和0<ϖi用于调整反正切函数arctan(·)输出值,κm是给定的函数κi()的下界.

考虑级联触发机制(8)的影响,控制器(8)变为

2.5 传感器和执行器故障建模

本文研究的自主卡车主要应用于矿区、码头等环境条件较差的场景,车辆的行驶状态容易受到扬沙、雾霾、水汽等条件的影响,导致车辆的执行器和传感器出现故障的问题[8].

考虑车载传感器的故障问题,对速度传感器、G-PS、陀螺仪和激光雷达传感器分别进行建模.速度传感器测量的状态变量

陀螺仪测量的状态变量

陀螺仪和GPS与激光雷达分别测量的状态变量

在传感器故障影响下,卡车系统的控制器(13)转换为

卡车的执行机构存在多种故障类型,如执行器卡死、常值故障、增益故障、偏差故障或几种故障组合等.本文考虑文献[9]中的执行器故障模型,第辆卡车的控制输入可被进一步描述为

其中:ufi为车队系统执行器故障后的控制输入,ρaci表示执行器的故障系数矩阵,对角矩阵

ρaci的数学期望为aci,如果aci=1,则表示第i辆车的执行器不存在故障,如果aci=0,则执行器发生卡死故障,如果0

2.6 网络故障建模

自主卡车的工作环境不仅会给传感器和执行器带来影响,同时也会造成V2V网络的故障问题.因此,本文考虑随机网络故障[10]对卡车队列系统造成的影响,并结合式(13),进一步得到在随机网路故障影响下第i辆卡车的控制输入为

其中:Kneti是控制增益.fi(xi-1(t))表示第i辆与第i-1 辆卡车之间的网络故障函数.βi(t)是随机变量,表示第i辆与i-1辆卡车之间发生网络故障的概率.

综合式(15)–(17)设计基于级联触发的控制器如下:

将式(18)带入式到(7)中,第i辆卡车的闭环系统可表示为

注2本文中考虑的网络故障有界,因此(18)中的故障满足以下条件:

其中Mi是一个已知的常数矩阵.

2.7 控制目标

本文目的是为非结构化弯曲道路上的卡车队列系统设计级联触发控制器,满足以下性能要求:

1) 单车稳定性.

2) 队列稳定性.

在车队的纵向上,领航车的任何操作所导致的震荡不会沿着车队向后逐渐放大,即对于任意w,有

γi(s)和γi-1(s)为车间距离误差γi(t)和γi-1(t)的拉普拉斯变换,距离误差γi=‖-R0‖.

3) 不存在Zeno行为.

对于基于级联事件触发的卡车队列系统,给定一个正定的最小触发时间间隔,保证所设计的级联触发控制器的采样时间大于最小触发时间间隔,即系统不存在Zeno行为.

3 级联触发控制器设计

本节将设计基于级联触发机制的控制器,实现控制目标1).首先给出如下系统渐近稳定的定理.

定理1对于给定的级联触发参数κm,随机网络故障概率期望,执行器故障期望aci,传感器故障期望si,网络故障上界矩阵Mi,以及系统增益矩阵Ki,Kneti,Li,如果存在正定矩阵Pi,Pi-1,使得以下矩阵不等式成立:

则闭环系统(19)渐近稳定.

证考虑如下李雅普诺夫函数:

根据无穷小算子,并结合(19)得到所对应的期望值为

同理可求得E{LVi-1(xi-1(t))},进一步得到

通过式(20)(25)–(26),应用自由权矩阵方法得到可得到

结合式(22),方程(27)可被重写为

进一步由式(22)以及Schur性质可得到:

证毕.

定理1为卡车队列渐近稳定提供了一个充分条件,下述定理2将给出稳定控制器设计方法.

定理2存在执行器故障、传感器故障以及随机网络故障的第i辆卡车闭环系统(19)满足渐近稳定条件,对于给定的级联触发参数κm,随机故障概率期望i,执行器故障期望aci,传感器故障期望si,网络故障上界矩阵Mi,如果存在Xi>0,Xi-1>0,Yi>0,Yneti>0,Zi>0,以及正定矩阵,,满足以下不等式条件:

控制器增益为

证明参考文献[5]定理2.

4 队列稳定性分析

在上一节中,主要对车队系统中单独车辆的稳定性进行分析.本节基于控制器(8)对卡车系统的纵向队列稳定性进行分析,实现控制目标2).

为分析卡车队列的纵向稳定性,设置δi=0◦,使车队沿纵向行驶.进一步得到车队相邻车辆之间的车间距离状态量为(t)=-vi(t)+vi-1(t),控制输入为ui(t)=ai(t).

由目标2)中距离误差的定义形式,可得到以下关于距离误差的公式:

进一步由式(8)得到卡车队列系统第i卡车的纵向控制输入为

将式(30)代入到式(29)中,关于距离误差的方程可被重写为

由于本文各跟随车辆采用相同的控制器,因此将系统的控制器增益统一为kvh,kR,Lvh.对式(31)进行拉普拉斯变换,得到

基于此传递函数,得到了以下关于车队队列稳定性的结论.

定理3卡车队列纵向误差系统(32),对于任意的w>0,有|γi(jw)/γi-1(jw)|≤1,如果满足以下条件:

证首先,将G(jw)写为以下形式:

因为a>0,如果车队是队列稳定,即满足

只需证明b≥0 即可.根据式(34)可知,如果满足条件(33a)(33b)(33c),则能够很容易得到,对于任意的w>0,有b≥0.证毕.

5 Zeno行为分析

Zeno行为是指在触发控制中,在有限的时间内发生无限次触发的现象,这种情况在实际车队控制过程中是不可实现的.为避免卡车队列系统出现Zeno行为,给出以下定理.

定理4对于满足式(22)的卡车队列系统(19)是渐近稳定的,并且当满足式(9)给定的级联触发条件时,其触发时间间隔存在正下界Tmin>0,满足

证明过程参考文献[8].

6 仿真

为了验证本文所设计控制器的有效性,本文利用MATLAB/Simulink软件对一个由1辆领航车和5辆跟随车所组成的车队,分别在直线和弯道两种路况下进行仿真,并与文献[7]中所采用的控制算法进行对比分析.本仿真中车辆模型的参数设置为

牵引车长度lh=8 m,半挂车长度lt=13 m,期望速度=18 m/s,期望车间距离R0=20 m,牵引车期望航向=00,半挂车期望航向=00,期望相对角度α0=0◦,期望跟随角度ϕ0=0◦.

在仿真部分,卡车队列系统的传感器故障参数设置 为ρs1=ρs2=...=ρs5=diag{0.8,0.75,0.7,0.85,0.8,0.8},执行器故障参数为

非线性网络随机故障函数为

自触发采用周期τk=0.05.故障界限系数为

通过计算得到的控制器增益为

6.1 直线道路场景

在直线道路场景下,车队中相邻车辆之间的初始距离为20 m,领航车和所有跟随车辆以相同的初始速度5 m/s行驶,领航车快速将速度增加至18 m/s,并沿道路保持匀速行驶.分别使用本文提出的控制器和文献[7]的控制器,控制所有跟随车辆跟随领航车.其相关状态信息分别如图3和图4所示,本文采用的级联触发方案所对应的触发信息如图5所示.

图3 本文控制器下直线道路卡车队列系统Fig.3 The truck platoon system on straight road under proposed controller

在本文提出的控制器下,车队中所有跟随车辆的最大速度和最大车间距离分别为20.4 m/s和21.8 m,且在10 s左右系统就达到了稳定状态,如图3(a)和3(b)所示.此外,从跟随车辆1 到车辆5,相邻车辆之间的车间距离幅值依次减小,满足车队的串稳定性.在相同的仿真条件下,采用文献[7]控制器,车队中车辆的最大速度和最大车间距离分别为24.8 m/s 和22.6 m,在15 s左右系统达到稳定,如图4(a)和4(b)所示.此外,车队随着车辆数量的增加,相邻车辆间的车间距离不断增大,整个车队系统不满足车队的串稳定性.通过对比可知,采用本文控制器的车队系统在超调量和收敛时间上都要优于采用文献[7]控制器的系统.图5给出了本文所采用控制器的触发瞬间和触发间隔,采用级联触发方案的触发次数为288次.通过计算可知,采用时间采样的触发次数为1200次,触发次数降低了76%,大大减少了触发次数,能够有效的提高车辆的平稳性和燃油经济性.

6.2 弯曲道路场景

车队中相邻车辆之间的初始距离为20 m,所有车辆的初始速度为0 m/s,领航车快速将速度增加至18 m/s,并沿道路保持匀速运动.通过分别使用本文提出的控制器和文献[7]的控制器,控制所有跟随车辆跟随领航车.其相关状态信息分别如图6和图7所示.

图6 本文控制器下的卡车队列系统Fig.6 The truck platoon system under proposed controller

图7 文献[7]控制器下的卡车队列系统Fig.7 The truck platoon system under controller in [7]

在本文提出的控制器下,在纵向上,车队中所有跟随车辆的最大速度和最大车间距离分别为18.7 m/s和21.5 m,如图6(a)和6(b)所示.此外,从跟随车辆1 到车辆5,相邻车辆之间的车间距离幅值依次减小,满足车队的串稳定性.在横向上,整个车队系统能够在较平滑的相对角度和跟随角度下(如图6(c)和6(d)所示),实现稳定的跟踪控制.在相同的条件下,使用文献[7]的控制器时,在纵向上,车队中车辆的最大速度和最大车间距离分别为26.6 m/s和23.4 m,比本文所采用的方法高出很多,如图7(a)和7(b)所示.此外,随着车辆数量的增加,相邻车辆间的车间距离不断增大,整个车队系统不满足串稳定性.在横向上,车队中车辆的相对角度和跟随角度如图7(c)和7(d)所示,其中的跟随角度抖动明显,角度变化的范围较大,没能实现稳定的跟踪效果.

通过对比可知,采用本文所设计的耦合控制器的控制器效果要优于解耦控制,特别是在横向上效果更加明显.

7 结论

本文研究了在非结构化弯曲道路上受到网络故障、传感器故障和执行器故障影响的卡车队列协同控制问题.利用卡车的运动学模型以及车辆间的位置关系,建立了弯曲道路下的车队模型,提高了车辆模型的精确性.设计基于自触发和事件触发的级联控制方案,极大缓解了故障的影响,并且有效降低了车辆控制信号的更新频率,减少了执行器的频繁操作,提高了车辆的燃油经济性.利用李雅普诺夫方法设计了保证车队渐近稳定和队列稳定的控制器.仿真结果表明本文算法的有效性.