快速平均一致与多采样率下储能系统精准功率分配

吴 涵 ,柴 利,田玉楚

(1.武汉科技大学信息科学与工程学院,湖北武汉 430080;2.浙江大学控制科学与工程学院,浙江杭州 310027;3.昆士兰科技大学计算机科学学院,澳大利亚 昆士兰州 布里斯班 4001)

1 引言

新能源发电的波动性、间歇性给智能电网安全稳定运行带来了新的挑战[1–3],而储能电池能够快速响应提供或吸收有功功率,相较于传统的大容量集中式储能,分布式储能系统可以实现灵活的即插即用,其功率的均衡分配是智能电网经济高效运行的前提[4–6].

现有储能电池功率分配大都是基于电池剩余电量(state-of-charge,SoC)一致、快速一致来设计的[7].Lu等[8]将自适应下垂控制系数设计为SoC值n次方的反比,通过调节n实现SoC和功率的平衡.Cai和Hu[9]设计了平均估计器和能量协调控制算法估计电池组需要输出的平均功率,对每个电池组的电流进行控制来实现输出功率的跟踪和SoC 平衡.Huang和Qahouq[10]对连接储能电池和母线电压的转换器进行分布式控制,同时实现了SoC平衡和电压稳定.Morstyn等[11]提出了基于非线性滑模控制的分布式同步控制算法,实现了SoC快速同步.

由于SoC变化率与功率大小成正比,当电池SoC初始值偏差较大时,基于SoC快速一致的功率分配方案会引起部分电池过分出力,轻则减少电池寿命,重则损坏电池甚至造成安全事故.于是,文献[12]提出一种基于相同相对SoC变化率的连续时间功率分配控制方案,使所有电池SoC值保持相同的相对变化率,从而在充满电或者放完电时同时达到SoC一致,避免出现某些电池过分出力的情况.注意到,当时间趋于无穷时,文献[12]对集总变量平均值的估计值与实际值之间存在静态误差.另外,在实际控制系统中,连续信号需要被采样为离散信号以用于数字计算设备的处理.因此,还需要在离散时间下进一步开发新的分布式控制方法,提高平均一致估计算法的精度,从而更好的实现基于相同相对SoC变化率的功率分配.

关于分布式平均一致的研究已经比较成熟[13–14].Xiao和Boyd[15]将快速平均一致问题转化为最优权重设计问题,得到了最优的收敛率.Aysal等[16]根据原始状态和预测状态值进行迭代更新,加快了分布式平均一致算法的收敛.文献[17–18]基于图滤波器设计得到有限时间实现平均一致的近似算法.Yi等[19]直观地揭示了一致性协议和图滤波的本质联系,建立了一致性协议及其收敛率与图滤波多项式设计的直接显式关系,给出了具有时变控制参数及周期时变控制参数的平均一致的充要条件,以及收敛率的精确表达式.

根据以上分析,本文设计了基于快速平均一致算法和多采样率的分布式功率分配控制方法,在电池单个控制周期内,设计参数时变的平均一致估计算法,快速精确地得到功率分配值,更精准的实现了基于相同相对SoC变化率的功率分配.本文主要贡献如下:

1)拓扑结构已知时,采用线性有限时间平均一致算法,其收敛时间与初始状态无关,只与拉普拉斯矩阵的非零非重特征根个数和算法采样时间有关,在有限时间内得到了准确的功率分配值,实现了基于相同相对SoC变化率的功率分配;

2)拓扑结构未知时,采用具有最优收敛率的平均一致算法,根据拉普拉斯矩阵非零特征根上下界设计周期时变的控制参数,快速得到了比时不变控制、单周期控制和基于等分点的多周期时变控制更精确的功率分配值,实现了基于相同相对SoC变化率的精准功率分配;

3)不仅加速了单个控制周期内快速平均一致算法的收敛率,而且给出了包含储能电池动力学和平均一致算法的整个控制系统的渐近稳定性分析.

2 模型建立与问题描述

考虑一个由n个储能电池构成的分布式储能系统(distributed energy storage system,DESS),每个储能电池的动力学模型为

其中:i=1,2,···,n,SoCi(t)为电池i在t时刻的电量状态,Qi为电池i的容量,ρi为电池i的库仑效率,Pi(t)为电池i的输出功率(Pi(t)>0)或输入功率(Pi(t)<0),Vi为电池i的端电压.令电池控制周期为T,将式(1)离散化可得

其中:k=0,1,···,SoCi(kT)和Pi(kT)分别为第k个控制时刻电池i的SoC和输出功率(或输入功率).

本文的控制目标是利用分布式控制方法,实现各储能电池功率的快速精准分配,保证供需平衡的同时,使得各电池以相同相对SoC变化率进行充放电.主要问题描述如下.

问题1假设总的发电量和需求量之间的不平衡功率为P,每个储能电池的输出功率或输入功率Pi(kT)需要满足以下两个条件:

2)每个电池以相同的相对SoC变化率进行充放电.

针对问题1,文献[20]提出了基于多采样率的分布式控制策略.为方便说明,首先给出各电池功率,以及相关变量定义.电池i的功率为

充电情况下的相对SoC变化率为

为避免用到式(3)中全局平均值,文献[20]采用分布式平均一致算法得到了全局平均值的估计值.注意到估计值的精度将直接影响到功率分配方案的实现.为了更快速地实现精准功率分配,本文进一步提出快速平均一致算法与多采样率相结合的控制方法.

用一个无向连通图G表示n个储能电池的通信拓扑,邻接矩阵A=[aij]∈Rn×n(i,j=1,2,···,n),其中aii=0,aij=1 表示电池i和j能够互相传递信息,否则aij=0.度矩阵D=[dii]∈Rn×n,其中dii=拉普拉斯矩阵为L=D-A,其特征根表示为0=λ1<λ2≤···≤λn.

其中:i=1,2,···,n,k′=0,1,···,m-1,β(k′)为时变参数,(kT+(k′+1)Te)是电池i对(kT)的估计值.T=(m+1)Te,Te为平均一致算法采样周期.当k′=0时,(kT+k′Te)=xi(kT),(kT+k′Te)=xj(kT).

注意到,算法(4)在经过m次迭代后得到(kT)的估计值i(kT+mTe).式(1)中各电池功率分配值Pi(t)可表示为

因此,式(2)可转化为

综上所述,问题1进一步转化为问题2.

问题2设计公式(4)中平均一致算法的时变参数β(k′),快速得到(kT)的精确估计值,从而实现功率的精准分配,使得下面的等式成立:

1)t ∈[kT+mTe,(k+1)T+mTe)时,

3 拓扑结构已知时有限时间分布式功率分配

首先给出通信拓扑结构已知时,一阶线性多智能体系统有限时间达到平均一致的结果.

引理1[19]对一个包含n个智能体的无向连通图G,假设其拉普拉斯矩阵有m个非零非重特征根λpk′(k′=0,1,···,m-1).智能体i的动力学为

其中:zi(k)为智能体i在k时刻的状态,控制输入

将引理1中的方法应用到(4)中的平均一致算法,定理1将给出有限时间实现基于相同相对SoC变化率功率分配的具体分析和证明.

定理1对一个包含n个电池的DESS,通信拓扑用无向连通图G表示.假设其拉普拉斯矩阵的非零非重特征根为λpk′(k′=0,1,···,m-1).令算法(4)中时变控制参数,每个电池功率如式(5)所示.当t≥mTe时,在有限时间内实现了基于相同相对SoC变化率的功率分配.

将式(9)两边同时乘以QiVi/ρi可进一步变换得到

由式(3)(10)可得

因此,在mTe时刻可以得到T时刻的准确功率分配值Pi(T).将(mTe)代入公式(2)依次迭代可得

上述分析表明,在mTe时刻得到(0)的准确估计值后,Pi(kT)(k=1,2,···)的值就可以计算出来,即Pi(kT)=Pi(mTe).

此时,各电池功率值可具体表示为

将式(11)代入式(2)–(3)可以得到

因此,t≥mTe时,问题2中条件1)和2)成立.证毕.

4 拓扑结构未知时的快速分布式功率分配

当通信拓扑未知时,无法得到拉普拉斯矩阵的特征根,然而已有文献提供了确定非零特征根上下界的方法[22].假设非零特征根满足λi ∈[a,b],引理2给出了基于最优多周期时变控制的快速平均一致算法.

引理2[19]对一个包含n个智能体的无向连通图G,拓扑结构未知,邻接矩阵A表示电池间的通信关系,智能体i的动力学模型为

其中:zi(k)为智能体i在k时刻的状态,控制输入

接下来进一步给出采用快速平均一致算法时,基于多采样率的快速精准功率分配及稳定性分析.

定理2对一个包含n个电池的DESS,通信拓扑G未知,其拉普拉斯矩阵L非零特征根的上下界为λi ∈[a,b].令算法(4)中β(jM+k′)=1/rk′,其中:k′=0,1,···,M-1,j=0,1,···,c-1.令m=cM,T=(m+1)Te,各电池输出功率或输入功率分配如式(5)所示,那么

1)对固定的k,在电池控制时刻kT和(k+1)T之间,估计误差与初始误差的关系为

其中:k=0,1,···,c为正整数,c≥2;

证由引理2可知,在电池单个控制周期内,平均一致算法收敛率ρM≤γM<1.算法(4)中的控制参数采用多周期时变控制序列时,在固定的采样时刻k,对(kT)的估计误差与初始误差关系可以表示为‖e(kT+mTe)‖2≤‖e(kT)‖2.

因此,在kT和(k+1)T之间,估计误差是递减的.接下来还需要证明,在电池每个采样时刻,集总参数xi(kT)与其全局平均值(kT)的误差ei(kT)也是递减的,从而说明整个控制系统渐近稳定.

以放电情况为例,将式(6)代入式(7)可得

两边同时乘以QiVi/ρi,进一步得到

在放电和充电情况下,xi(kT)是递减的,根据式(13)可知

于是,当t →∞时,放电情况和充电情况分别有

满足问题2中的条件1)–2).证毕.

注1拓扑结构未知时,如果依次取M个点将非零特征根上下界区间进行等分,即

对式(4)中的平均一致算法,若采用时不变控制,当β=(a+b)/2 时,收敛率最快,为ρ=(b-a)/(b+a)[21].而采用最优多周期时变控制时,收敛率γM<(b-a)/(b+a).c=1时为单周期控制,估计误差收敛率为γM;c≥2时为多周期控制,收敛率为.由于γM<1,<γM.另外,文献[19]表明,根据特征根区间等分点倒数设计时变控制参数时,收敛率γM∗>γM.因此,采用最优多周期时变控制序列的平均一致算法,能更快的得到比时不变控制、单周期控制和基于等分点的多周期时变控制更精确的估计值,从而得到精确的功率分配值,更精准的实现了基于相同相对SoC变化率的功率分配.

注2对一个包含n个节点的无向连通图,其拉普拉斯矩阵非零特征根上下界满足2/n≤λi≤n(i=2,···,n)[22].拓扑结构未知时,定理2仅需用到节点个数信息得到拉普拉斯矩阵非零特征根的上下界,再根据上下界来设计快速平均一致性协议的时变参数,给出了基于快速平均一致算法和多采样率的功率分配控制方法.因此,节点个数一定时,在保证无向网络连通的前提下,所提方法适用于任一拓扑结构.

5 仿真实验与分析

假设DESS由8个储能电池组成,参数设置如表1所示.本节将针对放电和充电两种工作模式来验证本文所给出的控制方法和主要结果.情况1为拓扑结构已知时,采用时变控制的有限时间功率分配结果,用于验证定理1.情况2为拓扑结构未知时,采用最优多周期时变控制时的功率分配结果,用于验证定理2.情况3为拓扑结构未知时,基于等分点的多周期时变控制结果,用于与情况2作对比.

情况1当拓扑结构已知时,假设8个储能电池的拓扑结构为一条无向路径.按照定理1设置控制参数,将控制参数设计为拉普拉斯矩阵非零非重特征根倒数由小到大组成的序列.放电和充电下的仿真结果分别如图1和图2所示.

图1 放电情况: 采用定理1中时变控制方法的仿真结果(拓扑结构已知)Fig 1 Discharging case: Simulation results with the timevarying method proposed in Theorem 1 (topology is known)

图2 充电情况: 采用定理1中时变控制方法的仿真结果(拓扑结构已知)Fig 2 Charging case: Simulation results with the time-varying method proposed in Theorem 1(topology is known)

图1(a)和图2(a)表明,在t=mTe=2.8 s 时得到d(0)和c(0)的准确估计值,di(2.8)=dj(2.8)=d(0),ci(2.8)=cj(2.8)=c(0).图1(b)和图2(b)分别给出了各储能电池输出功率和输入功率.如图1(c)和图2(c)所示,在放完电或者充满电时同时达到SoC一致,并且各储能电池具有相同的相对SoC变化率(如图1(d)和图2(d)所示).

情况2拓扑结构未知时,假设λi ∈[0.25,8],采用最优多周期控制方法来估计全局平均值,控制参数根据定理2进行设计,放电和充电下的仿真结果分别如图3和图4所示.

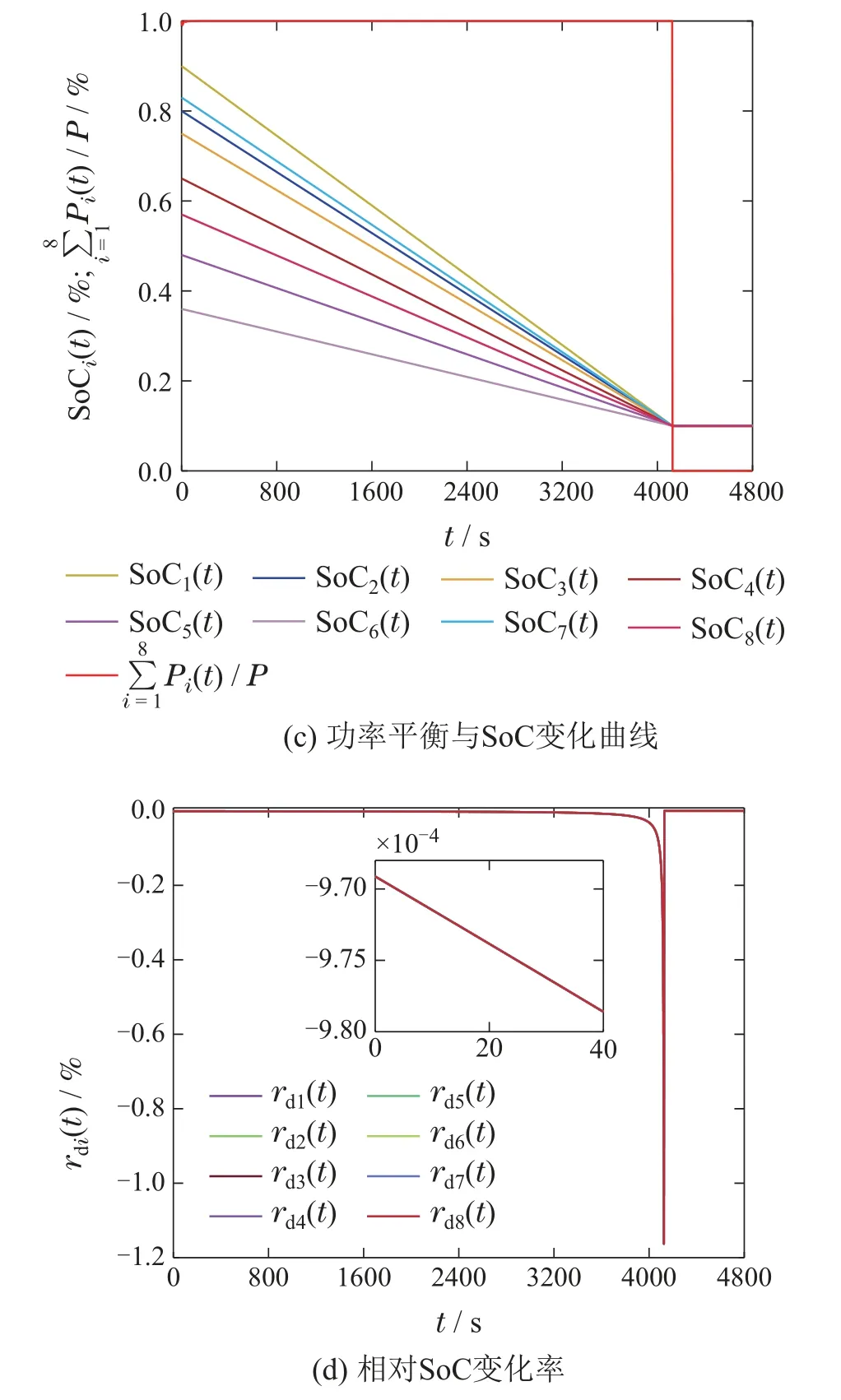
图3 放电情况: 采用定理2中最优多周期时变控制方法的仿真结果(拓扑结构未知)Fig 3 Discharging case:Simulation results with the optimal multi-periodic time-varying method proposed in Theorem 2(topology is unknown)

图4 充电情况: 采用定理2中最优多周期时变控制方法的仿真结果(拓扑结构未知)Fig 4 Charging case: Simulation results with the optimal multi-periodic time-varying method proposed in Theorem 2(topology is unknown)

情况3拓扑结构未知时,采用基于等分点的多周期控制方法来估计全局平均值,放电情况下的仿真结果分别如图5所示.

图5 放电情况: 采用基于等分点的多周期时变控制方法的仿真结果(拓扑结构未知)Fig 5 Discharging case: Simulation results with the multiperiodic time-varying method based on points in[a,b]with equal distance(topology is unknown)

由于平均一致算法的时变参数仅用到非零特征根上下界的信息,而非零特征根上下界仅和节点数有关,因此,在节点个数不变且网络连通的情况下,拓扑结构变化不会影响仿真结果.仿真时情况2和情况3中各电池的通信拓扑与情况1相同,为一条无向路径.

与图5(a)相比,图3(a)中的估计值更快趋近于实际值.图3(b)中各电池功率在初始波动阶段比图5(b)中功率更加稳定.图3(c)中不平衡功率与电池总功率比值在初始波动阶段比图5(c)更稳定.图3(d)中各电池相对SoC变化率在20 s时的偏差远远小于图5(d)分别在40 s时的偏差.结果表明,与采用基于等分点的多周期时变控制相比,最优多周期时变控制能更快更精准的实现功率分配策略.

6 结论

本文针对具有连续时间动力学模型的储能系统,提出了基于快速平均一致和多采样率的离散时间控制策略,实现了快速精准功率分配.不同于传统连续时间控制方法仅分析了平均一致算法的收敛性,没有考虑包含储能电池动力学和平均一致算法的控制系统的稳定性,本文不仅建立了估计误差的精确表达式,而且给出了整个控制系统的稳定性分析.在电池单个控制周期内,平均一致算法快速精确的估计出计算功率分配值需要的全局平均值.储能电池拓扑结构已知时,在有限时间内得到了准确的功率分配值;拓扑结构未知时,以更快的收敛率实现了比时不变控制、单周期控制和基于等分点的多周期控制更精确的功率分配.理论分析表明,所提方法实现了基于相同相对SoC变化率的快速精准功率分配.最后,通过仿真实验验证了所提控制策略的优越性.