冰磨损作用下天然浮石混凝土的寿命可靠性评估

王萧萧,高宇涛,荆磊*,刘曙光,闫长旺,姜琳

(1. 内蒙古工业大学土木工程学院,内蒙古 呼和浩特 010051; 2. 内蒙古自治区土木工程结构与力学重点实验室,内蒙古 呼和浩特 010051; 3. 生态型建筑材料与装配式结构内蒙古自治区工程研究中心,内蒙古 呼和浩特 010051; 4. 内蒙古工业大学资源与环境工程学院,内蒙古 呼和浩特 010051)

流凌期黄河内蒙古段时常发生冰凌现象,冰凌摩擦会导致混凝土材料的胶结性能降低,使保护层剥落、骨料暴露,不仅造成经济损失,还降低了水利工程的服役性能和使用寿命[1].天然浮石混凝土具有轻质、高强、保温、耐火、抗震性好等优点[2-3],可利用内蒙古储量丰富的浮石骨料制备天然浮石混凝土代替普通混凝土,以改善水利工程基础设施性能.为了进一步提高天然浮石混凝土在冰磨损作用下的服役寿命,设计贴近服役环境的冰-天然浮石混凝土磨损试验,并寻求合适的可靠性评价方法对于提升水利工程结构的安全性具有重要意义.

国内外研究学者关于冰-混凝土磨损的研究主要集中在影响因素方面,FIORIO[4]研究了3种因素(滑动速度、法向应力与结构粗糙度)对冰-混凝土磨损量的影响,发现增大试块表面粗糙度对其磨损率的增加起到了正向作用,然而当试块表层水泥浆破损时,其磨损率不再受粗糙度的影响.但在FIORIO探究冰滑动速率对混凝土磨损量影响的研究中,其设定的冰滑动速率参数过低,并不能有效模拟现实中冰的漂流速度.MØEN等[5]在FIORIO的基础上提高了滑动速度并研究了混凝土强度与接触冰压、环境温度对冰-混凝土磨损率的影响,发现提高试件强度、降低冰压或提高环境温度可明显降低冰-混凝土磨损率.除了研究外在因素对混凝土磨损的影响,学者们还对影响混凝土磨损的内在因素进行了探究.罗发胜等[6]探究了机制砂对混凝土耐磨性的影响,发现当机制砂的砂率达到34%时可大幅度降低混凝土磨损量.王萧萧等[7]以骨料体积分数、胶凝材料硬度、水胶比为试验变量,研究了冰-天然浮石混凝土磨损量的演变规律,发现其磨损深度随骨料体积分数与水胶比的增大而增加,随着胶凝材料硬度增大而减小.然而以上研究均重点关注的是在不同影响因素下,混凝土磨损量或磨损率的规律特征,未对其进行定量表征.为解决这一问题,MØEN等[8]选择Weibull分布将磨损率进行概率表示,并以环境温度、冰压与混凝土强度作为已知参数建立了预测冰-混凝土磨损率的多元线性回归方程,对混凝土磨损率进行了定量表征,并对海上灯塔混凝土的磨损深度进行了估计,相比于测量值其误差约为23%,预测效果并不理想.以上研究对各类因素影响混凝土磨损率或磨损量的发展进行了定性分析或定量表征,但依据磨损率或磨损量评估天然浮石混凝土寿命可靠性以及提高其安全性的研究较少.

鉴于此,文中以天然浮石混凝土为试验对象,设计接触冰压、环境温度和混凝土强度等级为试验变量,对其在冰磨损作用下寿命的可靠性进行分析研究,并预测在冰磨损作用下的极限寿命,希望能对黄河内蒙古段防治冰凌磨损天然浮石混凝土提供重要的工程参考价值.

1 试验材料及方案

本试验依照《轻骨料混凝土应用技术标准》(JGJ/T 12—2019)及《水工混凝土试验规程》(SL/T 352—2020)制备强度等级为LC20,LC30,LC40天然浮石混凝土(试件尺寸:100 mm×100 mm×400 mm),配合如表1所示,表中M为各成分配合,p为混凝土28 d抗压强度.

表1 天然浮石混凝土各成分配合

为评估天然浮石混凝土在冰磨损作用下寿命的可靠性,参照文献[9]并依据黄河宁蒙河段冰期气温特征[10-11],选取冰期日均气温-20～0 ℃为环境温度变量T,选取冰期月平均气温-10 ℃进行不同冰压的浮石混凝土磨损试验;为避免试验中冰柱出现破碎从而对磨损试验造成影响[12],以冰压pi(1～5 kPa)为试验变量进行浮石混凝土磨损试验;已有文献的研究表明不同冰压下受环境温度影响的混凝土磨损率演变趋势基本一致[5],根据规律文中参考文献[12]选择了冰压3 kPa来探究环境温度对浮石混凝土磨损的影响,为此设计了多种工况的冰-天然浮石混凝土磨损加速试验,如表2所示.

表2 试件试验工况

图1为冰-混凝土磨损加速试验装置[9].在图1中,装置包括电动机、往复机、固定支座、环形低温水槽、低温恒温水浴箱.环形低温水槽与低温恒温水浴箱连接,通过泵送低温冷却液提供低温环境.图2为冰-天然浮石混凝土磨损试验示意图.如图所示,将天然浮石混凝土切割成35 mm×45 mm×180 mm的试块,在试块切割面(图2中有蓝色标记的切面)上均匀选取5个标记点(Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ),并用电子螺旋测微仪记录每个标记点的初始厚度h0.将试块放入磨损装置底部的固定支座上,在试块上方的环形低温水槽内依次放入冰柱与砝码,通过调控槽内冷却液的温度与砝码质量控制环境温度与冰压.启动磨损装置,使冰柱以0.3 m/s在试块标记点上往复滑动磨损,当冰柱往复滑动到达规定磨损路径后用电子螺旋测微仪再次记录每个标记点的剩余厚度hs.累计磨损量Δh可通过剩余厚度hs与初始厚度h0的差值求得,即Δh=h0-hs.

图1 冰-混凝土磨损加速试验装置

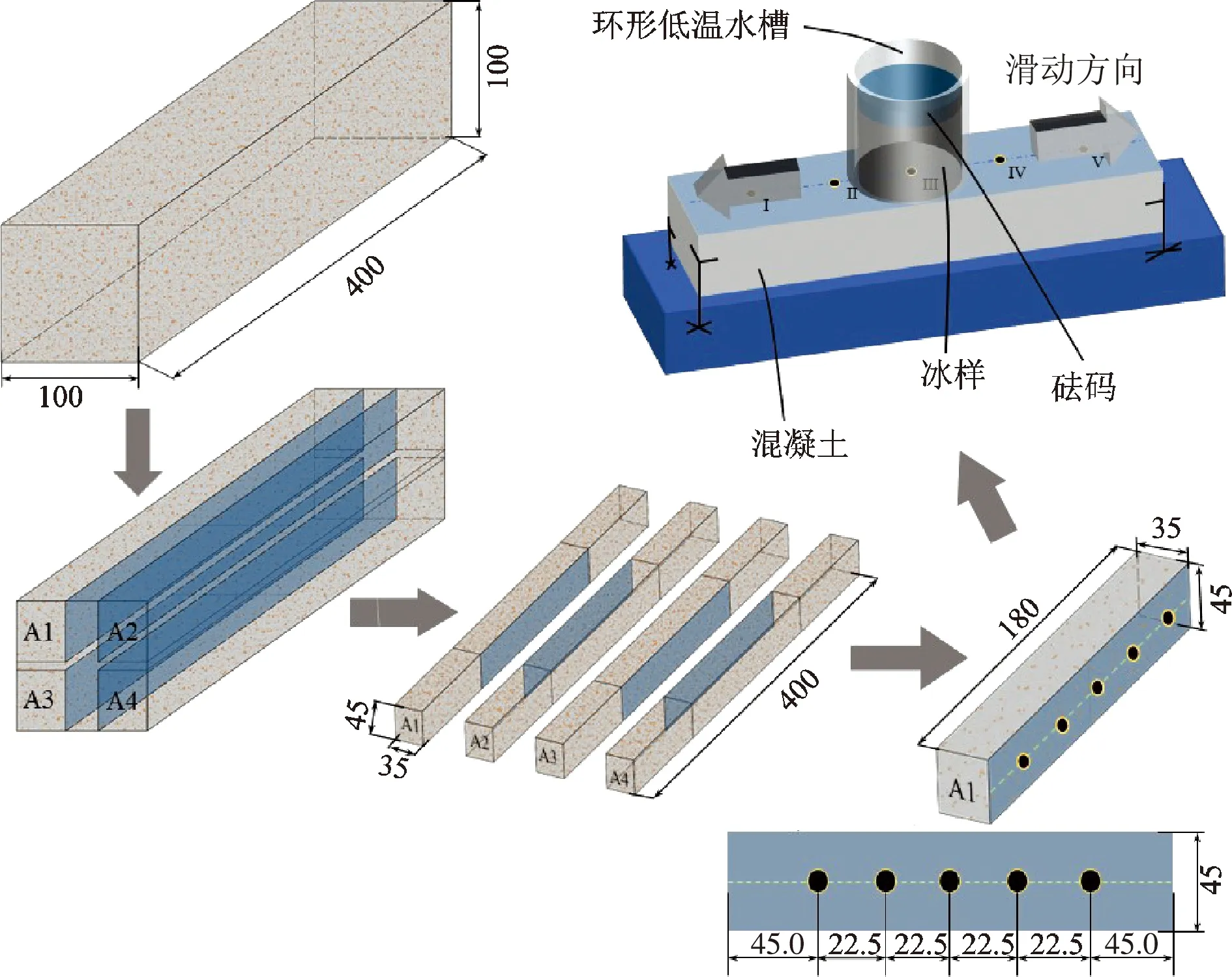
图2 冰-天然浮石混凝土磨损试验示意图(单位:mm)

2 冰磨损试验结果

图3为多种工况下天然浮石混凝土累计磨损量变化曲线图.从图中可以看出,所有工况下试块的累计磨损量均随磨损路径S呈线性递增趋势,表明受冰磨损作用的试块磨损程度在逐渐加重,其骨架结构遭受破坏,耐磨性在稳定衰减.这是由于试块表面裸露了粗糙的天然浮石骨料,在往复滑动过程中施加的冰压导致粗糙试块表面产生裂纹且冰压越大越促使裂纹形成;在接触压力作用下,接触区域的液相流体压力增大,渗入出现裂纹且多孔的试块内,进而破坏界面过渡区,导致砂浆微粒流入接触区域;与此同时在水平荷载与疲劳磨损作用下冰对试块的孔壁及表面粗糙处施加剪切应力,致使孔壁及粗糙处断裂,产生的微粒碎屑随冰柱滑动造成试块表面刮擦[13],进一步加重了浮石混凝土的磨损程度.从图3b还观察到,累计磨损量随环境温度降低而增大,这是由冰的剪切强度随温度降低而增加导致的结果[9].值得注意的是,环境温度为-15 ℃与-20 ℃时,累计磨损量演变程度相似,这是因为较低的环境温度使得冰与试块之间的水膜减少[9],形成了低粗糙的冰层,由此减弱了试块受冰磨损作用的影响,延缓了试块耐磨性的退化进度.

图3 天然浮石混凝土累计磨损量

3 寿命可靠度模型

3.1 可靠度模型的选择与建立

文中以冰磨损作用下天然浮石混凝土的累计磨损量为退化特征值,在累计磨损量达到阈值时,定义对应的磨损路径为失效寿命X.假设冰磨损作用下天然浮石混凝土的失效寿命X服从Weibull概率分布,则概率分布函数F(X)为

(1)

式中:U为尺度参数,调控分布曲线的大小;V为形状参数,影响分布曲线的形状,二者均可影响产品失效机制与产品性能退化轨迹[14].

根据规范《水工建筑物抗冲磨防空蚀混凝土技术规范》(DT/L 5207—2021),抗冲磨混凝土钢筋保护层厚度不得小于100 mm,即天然浮石混凝土的累计磨损量阈值为100 mm.对磨损加速试验中试块的累计磨损量随磨损路径的演变规律进行线性回归,依据累计磨损量阈值求得失效寿命X,并以此寿命数据对Weibull分布进行A-D检验[15].首先给定检验水平α=0.05,当P值≥α时不否认原假设,同时为提高小样本数据中拟合优度的准确率,参照文献[16]将A-D检验中AD统计量与临界值AD*进行对比,当AD值小于临界值AD*时,可知失效寿命X服从Weibull分布.检验结果如表3所示,表中P值均大于0.05,且AD值小于临界值AD*.由此可确认失效寿命X服从Weibull概率分布.根据Weibull概率分布函数F(X)与可靠度函数R(X)的关系,即F(X)+R(X)=1,可建立Weibull分布可靠度函数R(X)为

表3 A-D检验

(2)

并可采用参数失效寿命X对可靠度函数进行参数估计.

3.2 参数估计

最佳线性无偏估计法(BLUE)和最小二乘法(LSE)常用于Weibull分布的参数估计[17],为对比2种估计方法对天然浮石混凝土在冰磨损作用下寿命可靠性的影响,文中采用BLUE与LSE对Weibull分布的形状参数与尺度参数进行估计.

3.2.1 最佳线性无偏估计法

在冰-天然浮石混凝土磨损加速试验中,5个标记点样本数满足BLUE对样本数量的规定,因此可采用BLUE对Weibull分布展开参数估计.将每个标记点的失效寿命数据升序排列,得到x1≤x2≤x3≤x4≤x5,依照式(3),(4)求解参数U,V.

(3)

(4)

式中:D(5, 5,i)与C(5, 5,i)为最佳线性无偏估计系数,g5, 5为校准系数,并由《可靠性试验用表》[18]给出.表4为基于BLUE的参数估计汇总表.

表4 基于BLUE的参数估计汇总表

3.2.2 最小二乘法

LSE是估计Weibull分布参数的一种简单实用的方法.将式(2)取双对数整理后可得

ln{-ln[R(Xi)]}+VlnU=VlnXi.

(5)

根据Glivenko定理与已知的标记点个数[19],R(Xi)可通过中位秩近似代替.将升序排列的失效寿命数据和中位秩[20]代入式(5),利用最小二乘原理求解参数U,V,如表5所示.

表5 基于LSE的参数估计汇总表

对比表4,5中的参数值,发现2种方法求得U值波动相对较小,但BLUE所得V值总大于LSE求得的V值,因此可靠度曲线的特征也随参数估计值的波动而不尽相同.

此外,V值较U值变化较大是因为在LSE中V值与多项指标有关[21],而U值可以依据已知的V值后计算得出,与其他参数取值关联较小,因而其波动较小.

4 可靠性寿命分析

为了反映不同工况与各参数估计方法对天然浮石混凝土寿命可靠性的影响,将表4,5中参数估计值代入式(2),得到天然浮石混凝土寿命可靠度R(X)曲线,如图4所示.由图可知,天然浮石混凝土寿命可靠度曲线呈现单调降低的三阶段分布:可靠度为1.0的安全服役阶段、可靠度下降的加速损伤阶段和可靠度降为0的无抵御防护阶段.其中,可靠度曲线的安全服役阶段表明,天然浮石混凝土的累计磨损量处于量变积累阶段,当其积累到一定程度时,天然浮石混凝土耐磨性出现衰减,但还未影响其安全性.

图4 天然浮石混凝土在冰磨损作用下的可靠度

加速损伤阶段是占比可靠度曲线最大的阶段,表明此阶段的累计磨损量已从量变进入到质变,耐磨性出现严重衰减,在加速损伤阶段对冰磨损作用下天然浮石混凝土进行寿命预测是提高其耐磨性与安全性的有效方法[20].观察图4b发现,试件的可靠度曲线在环境温度为-15 ℃与-20 ℃下几乎重合.这与图3中2种温度下累计磨损量的变化规律是一致的.

对比图4中2类方法计算的可靠度,发现2类可靠度曲线的各阶段的退化时间与退化速率不尽相同.

基于BLUE算法的曲线安全阶段寿命略大于基于LSE算法的安全阶段寿命.在可靠度下降初期也是如此,然而在可靠度下降后期,基于2种方法的可靠性寿命大小关系出现反转,即基于BLUE算法的可靠性寿命小于基于LSE算法的可靠性寿命.当天然浮石混凝土可靠度R(X)为0.5时,对应的可靠性寿命与磨损加速寿命较为接近,如图5所示,即该可靠性寿命为天然浮石混凝土在冰磨损作用下的极限寿命.

图5 各工况下可靠性寿命与磨损加速寿命

表6为2类参数估计方法下天然浮石混凝土冰磨损路径预测值S,分析表6可以知道,最小二乘法预测的极限寿命最小,以此预测寿命作为天然浮石混凝土的极限寿命在可靠性工程上是合理的,同时也符合天然浮石混凝土材料结构关于安全储备的要求.

表6 天然浮石混凝土冰磨损路径预测值

5 结 论

1) Weibull分布对加速试验的寿命数据有较高拟合精度,且三阶段分布的可靠度曲线有效描述了多种工况的冰磨损作用下天然浮石混凝土耐磨性衰减进程,其中加速损伤阶段的占比最大,天然浮石混凝土耐磨性衰减程度加重.

2) 2种参数估计方法对比中,形状参数值受方法影响差异较大,而尺寸参数值变化幅度较小.2种方法求得可靠度下降的前后期可靠性寿命大小出现反转,LSE算法计算可靠度下降初期的可靠性寿命短,后期可靠性寿命长.

3) 当可靠度为0.5时,对应的可靠性寿命与天然浮石混凝土的磨损加速寿命较接近,该可靠性寿命定义为天然浮石混凝土在冰磨损作用下的极限寿命,其中LSE预测的天然浮石混凝土可靠性寿命更符合结构安全储备要求.