琴键阶消能工消能特性

赵一名,朱李英,李永业*

(1. 太原理工大学水利科学与工程学院,山西 太原 030024; 2. 四川水利职业技术学院,四川 成都 611231)

在灌区水利工程中,水库是供给农作物用水的水工建筑物,而消能问题是灌区水库安全的重中之重.阶梯式消能作为一种重要的消能方式已经有几千年的历史[1].到了现代社会,人们发现使用阶梯式消能是在溢洪道壁面的台阶上产生水跃进行消能[2],这种消能方式具有较高的效率.

近年来,阶梯式消能一直是国内外关注的焦点.杨吉健等[3]为探究台阶溢洪道的复杂水力特性,提出了相对消能率的概念.马朋辉等[4]通过模型试验对比分析了光滑溢洪道与台阶溢洪道的水力特性规律,并在台阶溢洪道引入了相对流速等水力特性的计算.但是由于台阶消能过程中,下泄水流流态复杂、水流速度分布不均匀,且台阶表面压强分布无法连续准确测量,因此,国内外使用数值计算与物理试验相结合的方式来研究台阶消能问题.

GÜVEN等[5]对一种变坡度的阶梯式溢洪道的掺气特性、流速特性、压强特性等进行了数值模拟,认为在阶梯式溢洪道数值模拟中,RNGk-ε模型的模拟结果与试验结果符合程度较好.杜金威等[6]使用RNGk-ε模型模拟并验证了台阶溢洪道的泄流过程,得出台阶面的消能效率与台阶级数有着较好的线性关系.赵相航等[7]采用VOF算法追踪自由水面,对阶梯式溢洪道消能的水力特性进行了研究.可见对于台阶消能问题,RNGk-ε湍流模型与VOF水面追踪算法有着较好的适用性.

台阶消能工在消能过程中其消能稳定性较为重要,需要避免产生过渡水流,因此台阶消能工在不同坡度、布置方式等情况下的消能效果也是研究的重点.于进伟等[8]对不同坡度和不同台阶高度的台阶溢洪道在不同单宽流量下滑行水流的消能特性进行了研究,认为非均匀流段上的相对消能率和台阶流程长度与水深比呈线性关系.ALTALIB等[9]对木制的阶梯式消能堰进行了试验研究,通过改变台阶的数量、台阶的高度以及消能堰坡度来分析消能堰下游产生水跃的特性,以节省下游消力池的长度,认为高度为36 cm的阶梯式消能堰的消能效果最理想.NASRABADI等[10]认为仅改变台阶坡度、布置方式等对消能效果的改善比较有限.

正是由于仅改变台阶坡度、布置方式等对改善消能效果不佳,近年来学者们提出了在溢洪道台阶表面添加消能工从而提升消能效果[11].HILO等[12]在1个3级台阶的溢洪道台阶表面添加半球状消能工阵列,或者在台阶表面进行打孔来改善溢洪道的消能特性.GHADERI等[13]在10级台阶的溢洪道台阶表面添加了块状消能工,认为添加消能工的确对台阶消能效果有益.但是,有些学者认为阶梯状的溢洪道表面本身就是一种消能工,可以直接改变台阶的几何形状而没有必要额外在台阶表面添加消能工.LI等[14]对改变台阶凸角和凹角形状的阶梯式溢洪道进行了数值研究,结果表明,改变台阶形状对于改善台阶表面压力分布有一定的效果.田忠等[15]、王磊等[16]分别提出了采用“V”形台阶与“M”形台阶的台阶消能工,并对其水力特性以及消能特性进行了分析.

文中拟提出一种琴键阶消能工,通过数值模拟与模型验证研究琴键阶消能工的消能特性.

1 数学模型的建立

1.1 控制方程

消能工进行消能的过程以Navier-Stokes方程为控制方程,并且在流动过程中满足连续性方程.诸多研究认为RNGk-ε湍流模型比较适合用于台阶消能问题[5-7],其相比于标准k-ε湍流模型(SKE)可提高涡旋产生处流动计算的精度,更好地模拟台阶上有剧烈三维旋滚的流动,因此文中采用RNGk-ε模型,即

紊动能k方程

(1)

紊动耗散率ε方程

(2)

式中:ρ为密度;x为坐标;k为紊动能;ε为紊动能耗散率;αk,αε分别为k和ε的普朗特数的倒数,两者均为1.39;μeff为有效黏度;C1ε与C2ε均为模型常数;Gk为紊动能产生项.

在消能过程中,水面线在各个位置随着时间不断变化,采用VOF算法追踪自由水面.VOF模型应用体积分数的方式,认为水与空气之间并无质量交换,通过同一组动量方程就可以描述水和空气的压力场与速度场.PISO算法采用非定常流动算法.消能过程中下泄水流的水面线处于不断变化的状态,使用非定常流动的PISO算法进行压力耦合计算.

1.2 边界条件

1) 入口边界:形成2个区域,即水流区域和空气区域.定义入口边界为2部分,水流区域设为速度入口并根据试验测得水深,空气区域设为压力入口.压力入口压强设为大气压强值.入口的紊动能k和紊动耗散率ε计算公式为

(3)

(4)

(5)

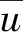
2) 出口边界:台阶出口边界选在流动充分发展的地方,即距离台阶末端0.6 m处设为出口边界;选用压力出流条件并设置为大气压强.

3) 台阶壁面边界:台阶壁面均设为固壁边界,即台阶壁面处无滑移.

4) 大气边界:台阶上方与自由大气接触设为压力边界,边界压力值设为大气压强.

1.3 网格无关性验证

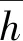
图1 网格无关性验证

从图1中可以看出,随着网格尺寸W的不断减小,该断面的平均水深也在不断地减小,且曲线的斜率越来越小.当网格尺寸继续减小到0.004 m时,如果再减小网格尺寸,平均水深基本保持不变,且网格尺寸为0.002 m和网格尺寸为0.004 m的数值模拟结果之间的相对误差只有0.4%.由此可知,当网格尺寸小于0.004 m后,其已经不是数值模拟结果的主要影响因素.将网格尺寸为0.004 m时的数值模拟结果与物理试验的测点数据进行水深与压强的对比后发现,两者最大相对误差不超过8.5%,说明将网格尺寸定为0.004 m能够满足试验要求.

1.4 网格划分

图2为琴键阶消能工计算域划分示意图(台阶消能工计算域划分与之类似).2种模型都采用非结构多边形网格划分并在台阶壁面处进行网格加密,y+≈30.网格最小尺寸为0.001 m,最大尺寸为0.004 m,网格划分结果如图2所示.其中,计算域入口高度H+h=220 mm,h为不同工况时试验实测水面线高度.

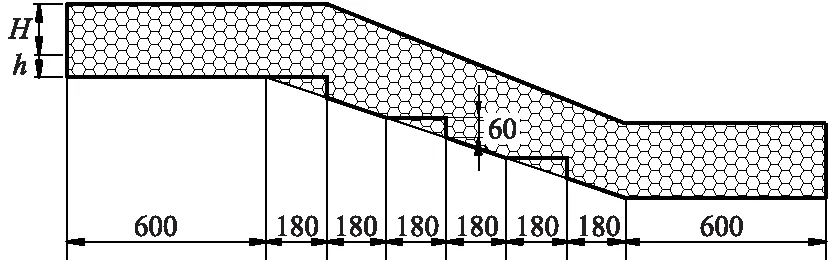
图2 计算域划分(单位:mm)

2 模型验证

2.1 消能工模型

图3为2种消能工示意图.琴键阶消能工的物理模型沿水平方向长2.28 m、宽0.2 m、高0.36 m,由台阶段、台阶上游段和台阶下游段组成.台阶上游段长0.6 m,宽0.2 m;台阶下游段尺寸同上游段;台阶段由斜坡与小台阶组成,斜坡坡度为1/3,高度为0.36 m,宽0.2 m,每个小台阶长0.18 m,宽0.067 m,高0.06 m,沿竖直方向均分6层布置台阶,第1,3,5层布置2个台阶,第2,4,6层布置1个台阶,如图3a所示.

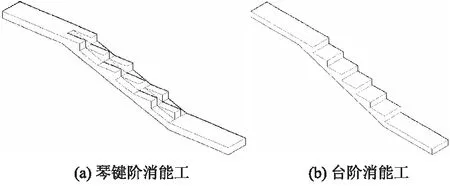
图3 2种消能工示意图

图4 试验系统布置图

台阶消能工的物理模型总体上与琴键阶消能工相同,不同之处在于台阶段都是高度为0.06 m,宽为0.2 m的台阶,如图3b所示.

2.2 试验系统布置

试验系统组成部分有测试段、整流器、输水管路、水箱、动力装置与流量计.试验时,动力装置将水流从水箱经过输水管路泵入整流段,使用调流阀可以调节流量;整流器平稳水流使得流量相对稳定;水流从整流段进入测试段,为防止水流溢出台阶模型两边的壁面,设计成高于该段的台阶模型;测试段前端为输水管路,将水输送回水箱,组成循环系统.

2.3 测试断面布置

图5为测试断面布置与测点布置.琴键阶消能工的6级台阶沿水流方向从上至下台阶标号分别为1#—6#;纵断面的布置以测试段入口左上方为零点,沿水流方向为X轴,横向为Z轴,模型高度为Y轴,沿水流方向共布置8个横断面,在其第3和第4级台阶上X为1.00,1.05,1.10 m处取横断面2#,3#,4#,在X=1.18,1.23,1.28 m处取横断面5#,6#,7#;而横断面1#位于台阶上游段X=0.20 m处,横断面8#位于台阶下游段X=2.08 m处;纵断面1#位于Z=0.18 m处,纵断面2#位于Z=0.10 m处,纵断面3#位于Z=0.20 m处;测点均在横纵断面的交线上.琴键阶消能工的断面布置和测点布置如图5a所示,台阶消能工的断面布置和测点布置与琴键阶消能工布置相同,如图5b所示.

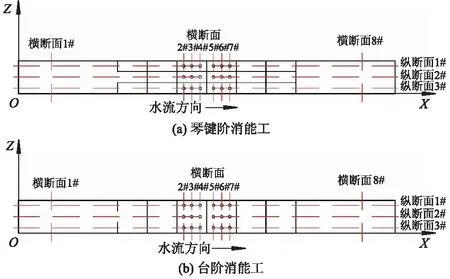
图5 测试断面布置与测点布置

2.4 模拟结果验证

图6为流量Q1=40 m3/h,Q2=50 m3/h,Q3=60 m3/h下琴键阶消能工在纵断面1#上第3级台阶和第4级台阶上的水面线高度和压强的数值模拟与试验实测结果对比,图中曲线下方的3和4为台阶标号,测点位于台阶上的位置由其横坐标给出.

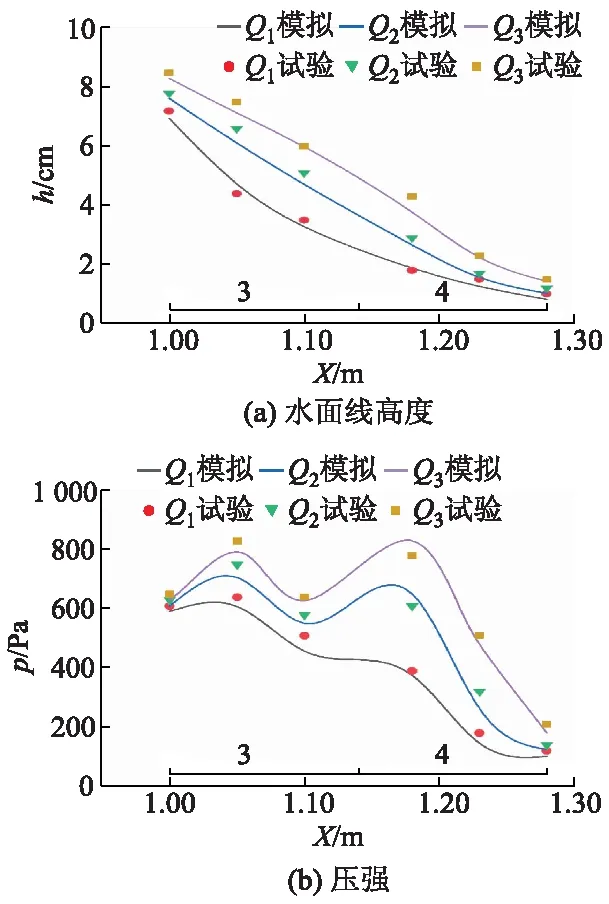
图6 数值模拟结果验证

经过验证,数值模拟的水面线与试验实测水面线基本吻合,最大相对误差为8.2%,数值模拟的压强与试验实测压强的最大相对误差为6.5%,证明对琴键阶消能工进行的数值模拟可行.

3 试验结果与分析

3.1 流态特征

台阶消能工水流流态划分理论是将水流流态划分为跌落水流、滑行水流以及介于两者之间的过渡水流.由台阶消能工纵断面的水体积分数分布判别局部流态特征.田忠等[15]将水体体积分数值V=0.55作为其是否为自由水面的临界值.

图7为Q=40 m3/h时水体积分数分布图.如图7a与7b所示,琴键阶消能工的水流流态在相同流量下比图7c台阶消能工的水流形态复杂得多.图7a中,纵断面1#水面线波动的幅度较大,在第2,4,6级台阶凸角处水面线的波动幅度到达极大值,具有明显的跌落水流的特点;在图7b中,纵断面2#水面线的波幅比图7a中的波幅要大得多,因此认为此时的流动形态也为跌落水流.综上所述,琴键阶消能工此时的消能流态为跌落水流.图7c台阶消能工中间断面处的水面线较为平缓,具有滑行水流“假想底层”的特点,同时又具有作为跌落水流典型特征的空腔存在,因此认为,此时的台阶消能工消能形态为过渡水流.

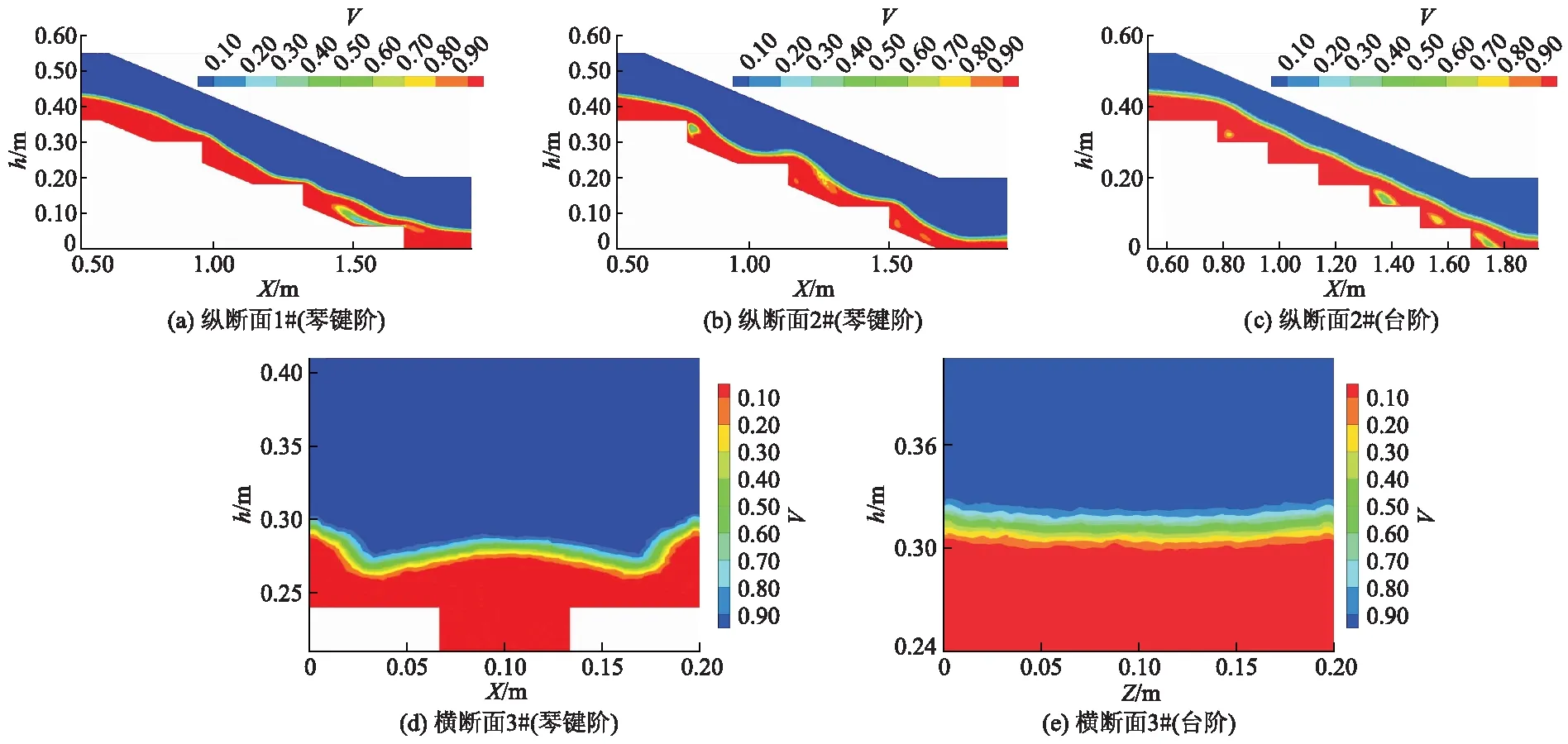
图7 水体积分数分布图

对于以上2种消能工的消能水流形态,普遍认为跌落水流是较好的消能水流形态;而过渡水流压强分布十分不稳定,容易引起共振等破坏性现象,实际工程中下泄的流量都应避免产生过渡水流.综上所述,Q=40 m3/h时琴键消能工纵断面1#和2#流态都类似跌落水流,可保障水工建筑物的整体安全.

图7d和7e为横断面3#的2种消能工水体积分数分布图.可以看出,琴键阶消能工流态复杂,主要表现为在台阶面上水深较浅,水流在台阶面上多方向下泄,在触及边壁时边壁水位壅高,靠近凹角处时会涌入凹角,水位较低,水面线与空气接触面积较大;而台阶消能工同一横断面内的流态在横向几乎无变化,且水面线与空气接触面积较小,水位相对较高.可见,同一横断面内琴键阶消能工水面线波动较大,与空气接触面积较大,更利于混掺空气进行消能.

3.2 压强特性

琴键阶消能工与台阶消能工在Q=40 m3/h流量下的壁面压强分布如图8a与8b所示.

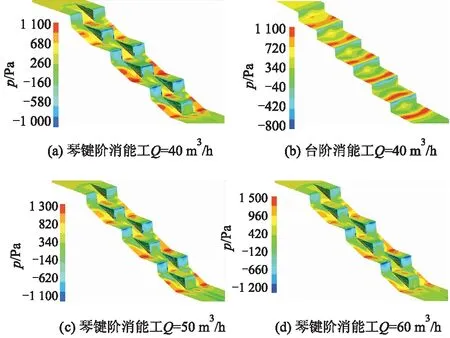
图8 2种消能工表面压强分布图

可直观地看出,在同一下泄流量下,琴键阶消能工的高压强分布区域在坡面以及台阶水平表面(远离台阶凸角)处相对较为分散,台阶消能工的高压强区域集中分布在台阶凸角处的水平面上.其原因在于,台阶消能工消能过程中,水流因为自身的惯性沿台阶下泄时直接冲击台阶凸角的水平表面;而琴键阶消能工由于表面相对复杂,下泄过程将水流分为多股,从每级小台阶下泄后冲击到坡面上以及坡面与水平面的连接处,这些位置都相对远离台阶凸角.而2种消能工的负压强区域都出现在台阶竖直表面.

对2种消能工的压强分布进行量化:以大于1.0 kPa为极大压强区域SD;小于0 Pa为负压强区域SF,对不同消能工在不同流量下的压强分布进行计算,如表1所示.琴键阶消能工的极大压强分布区域占消能工总面积S百分比均低于同一流量下的台阶消能工,并且在流量较高时,2种消能工的极大压强分布面积百分比差距进一步加大;对于负压强分布面积百分比,也存在类似情况.总体上,琴键阶消能工相对于台阶消能工,极大压强及负压强区域占该消能工面积的百分比都有所降低,并且台阶消能工的极大压强区域与负压强区域毗邻,在台阶凸角两侧易引起严重空化的压强分布,而对于琴键阶消能工,极大压强区域与负压强区域相距较远,尤其是极大压强区域远离台阶凸角,琴键阶消能工消能过程中下泄水流对凸角的安全影响较小.

表1 2种消能工在不同流量下的压强分布情况

3.3 流速矢量特性

消能过程实际上就是通过几种摩擦作用使水流的动能转化为内能的过程,一是固壁边界对水流摩擦的摩阻作用;二是提高水流的紊动程度,水流的流体质点相互摩擦消耗动能;三是提高水流与空气的混掺程度,水流与空气2种流体质点相互摩擦消耗动能.所以消能效果可以通过整个消能过程中下泄水流的流速矢量特性来体现.相同流量(Q=40 m3/h)下泄水流在琴键阶消能工纵断面2#、横断面3#与台阶消能工纵断面2#、横断面3#的流速矢量如图9所示.对比两纵断面,琴键阶消能工在横断面3#位置处可见在小台阶上方有2个较大的旋滚、小台阶内侧有2个较小的旋滚,台阶消能工在同一横断面处流速矢量并未显示出旋滚;结合其纵断面2#中流速矢量分析,认为琴键阶消能工该位置处下泄水流中旋滚为多个三维旋滚,而台阶消能工同一位置处下泄水流为1个二维旋滚.从流速矢量分布上可以看出,由于琴键阶消能工表面的边界条件相对台阶消能工较为复杂,因此其下泄水流中的旋滚较多且这种三维旋滚形式更有利于消耗下泄水流的动能.

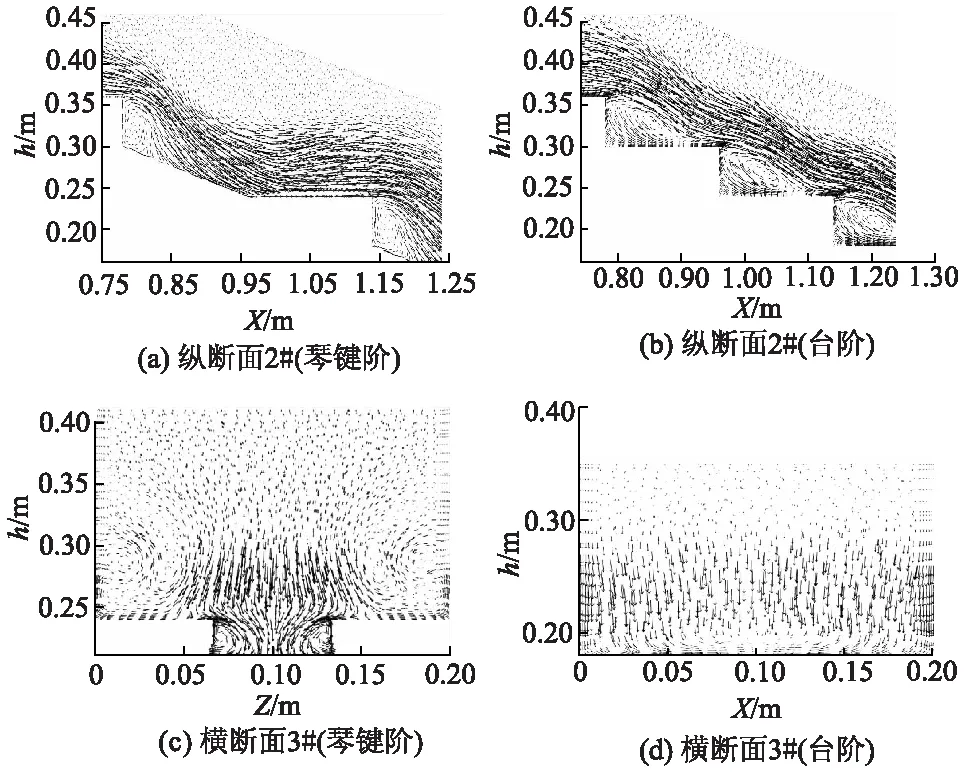
图9 断面流速矢量图

3.4 消能率

消能率是衡量消能工性能最重要的指标,文中对琴键阶消能工与台阶消能工的消能率进行计算.处于消能过程中的水流是非恒定流,消能工上游与下游水流平稳处(横断面1#与横断面8#)都可视作恒定流,在两横断面间应用能量方程,消能率计算公式为

(6)

(7)

(8)

式中:α1与α2分别为横断面1#与8#的动能修正系数;g为当地重力加速度;E1,E2分别为横断面1#与8#的总水头;η为消能率,v1,v2分别为消能工上、下游横断面1#和8#处平均流速.

表2为2种消能工在不同流量下的消能率.

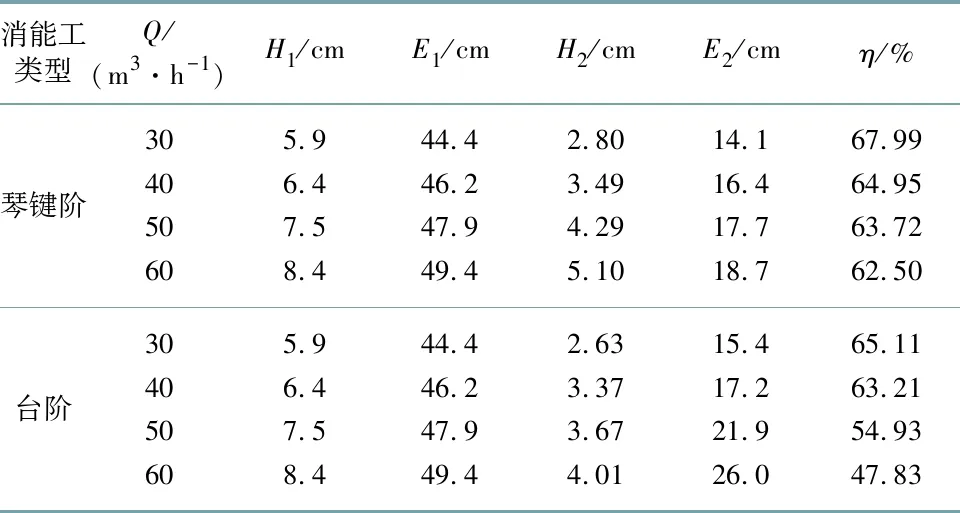
表2 2种消能工在不同流量下的消能率

由表2可知,Q=30 m3/h与Q=40 m3/h下这2种消能工的消能率之差分别为4.23%和2.68%,两者相差不大;但是在Q=50 m3/h与Q=60 m3/h时,2种消能工的消能率之差分别为13.79%和23.47%,两者相差较大.并且琴键阶消能工在同一下泄流量时消能率都要高于台阶消能工.在消能稳定性方面,由于2种消能工在Q=30 m3/h与Q=40 m3/h时消能率都变化不大,较为稳定.因此,以Q=40 m3/h为基准增大流量25%时(从Q=40 m3/h增大到Q=50 m3/h),琴键阶消能率下降了约1.89%,台阶消能率下降了13.1%;增大流量50%(从Q=40 m3/h增大到Q=60 m3/h),琴键阶消能率下降了约3.22%,而台阶消能率下降了24.33%.琴键阶消能工在加大流量条件下消能率变化幅度较小,而台阶消能工加大相同流量时,消能率下降幅度较大.在文中研究的流量范围内,增大流量对于琴键阶消能工的消能率影响较小,可见琴键阶消能工消能过程较为稳定.

4 结 论

1) 相同下泄流量(Q=40 m3/h)时,琴键阶消能工流动形态尚为跌落水流,而台阶消能工流动形态已为过渡水流,琴键阶消能工的消能流态较好.

2) 琴键阶消能工表面的压强分布显示:极大压强区域与负压强区域相隔较远,与台阶消能工凸角两侧极大压强区域和负压强区域毗邻分布不一样,因此对于台阶凸角的影响较小;琴键阶消能工表面的压强分布对于消能工安全性更有保障.

3) 在相同下泄流量时,琴键阶消能工的下泄水流三维旋滚较多,其流动的紊动程度较台阶消能工的二维旋滚情况流动的紊动程度高,且对于耗散水流动能效果较好.

4) 在文中所研究的范围内,琴键阶消能工随着流量的增大(Q=40 m3/h增大到Q=60 m3/h),其消能率下降3.22%,而台阶消能工在相同情况下消能率下降24.33%.同一下泄流量时,琴键阶消能工消能率都大于台阶消能工的消能率,并且琴键阶消能工相比台阶消能工的消能过程较为稳定.