基于多函数交叉的地表动态沉陷预测模型及应用
王文才 ,吴周康 ,王 鹏 ,苏保山 ,杨少晨
(1.内蒙古科技大学 矿业与煤炭学院,内蒙古 包头 014010;2.国能乌海能源五虎山矿业有限责任公司,内蒙古 乌海 016000)
煤炭开采过程中,采区岩体内部原有的力学平衡状态被破坏,引起了地表的移动变形,并进一步容易诱发多种地质灾害[1]。工作面开采过程中采空区的形成使得岩体内部形成空腔,原岩应力转变为扰动应力,且上覆岩层在自重以及其他岩层应力的叠加作用下,使得覆岩发生运移破坏。这种破坏随着工作面的推进,由起初的覆岩移动发展为垮落,进一步发展至关键层形成破断再进而发展至地表形成地表的沉陷[17]。地表沉陷的危害性尤其严重[2-3]。因此开展地表沉陷预测成为采矿工程中重要的一项工作[4-6]。针对这一问题,郭惟嘉等[7]通过现场与理论相结合的分析手段,对翟镇煤矿采动下地表移动规律进行了分析,得出了地表非连续移动的诱发因素是覆岩的结构与采深与采高的比值;刘宝琛等[8]引入概率积分法并进行改进,为我国地表移动规律研究指出了更加明朗的研究方向;刘诗杰等[9]将数值模拟与概率积分法配合使用,对由于工作面开采而造成的地表沉陷进行了准确的预测,有效保证了地表建筑物的安全;张世良[10]使用地表监测点实测数据对概率积分法地表沉陷预测参数进行反演,从而做到对地表沉陷的二次预测;郭瑞瑞[11]通过对布尔台矿区工作面开采沉陷规律的研究,得到地表下沉的特点为启动速度快,稳定态缓慢;韩亚鹏等[12]以观测站实测数据为基础,通过建立概率积分法时间与坐标的预测函数,对开采任意过程进行了地表沉陷的预测。
上述研究多集中于静态的下沉预测,然而地表沉陷是1 个时间和空间上的动态过程,因此针对这一特征需做出动态下沉预测[13]。张兵等[14]、崔希民等[15]通过运用一系列的时间函数从不同的角度,对地表沉陷动态预测的理论与方法进行了改进与提高。然而针对不同的工况条件,需要对其做出不同的改进。为此,在以往学者的基础上[16],通过将 Knothe 时间函数、概率积分法以及 Usher 函数相结合,构建出动态沉陷预测模型,并结合数值模拟与现场实测验证了模型公式的实用性与准确性,可为其他工作面开采地表沉陷预测提供参考。
1 地表预测时间函数与概率积分交叉
1.1 Knothe 时间函数
Knothe 在分析工作面开采形成的地表下沉与时间上的关系时,对一假定点在时间为t时刻监测到的下沉速度为dW(t)/dt与此点的最大地表沉陷值Wmax与动态沉陷函数W(t)的差值为反比,则有:
式中:A为与上覆岩层性质有关的影响系数;Wmax为地表最大沉陷值,mm;t为沉陷发展时间,d。
对式(1)积分,并对初始时间取0,初始沉陷值取0,可得:
令时间函数f(t)=1-e-At,则式(2)可表示为:
1.2 时间函数结合概率积分法
走向主断面沉陷原理分析图如图1。
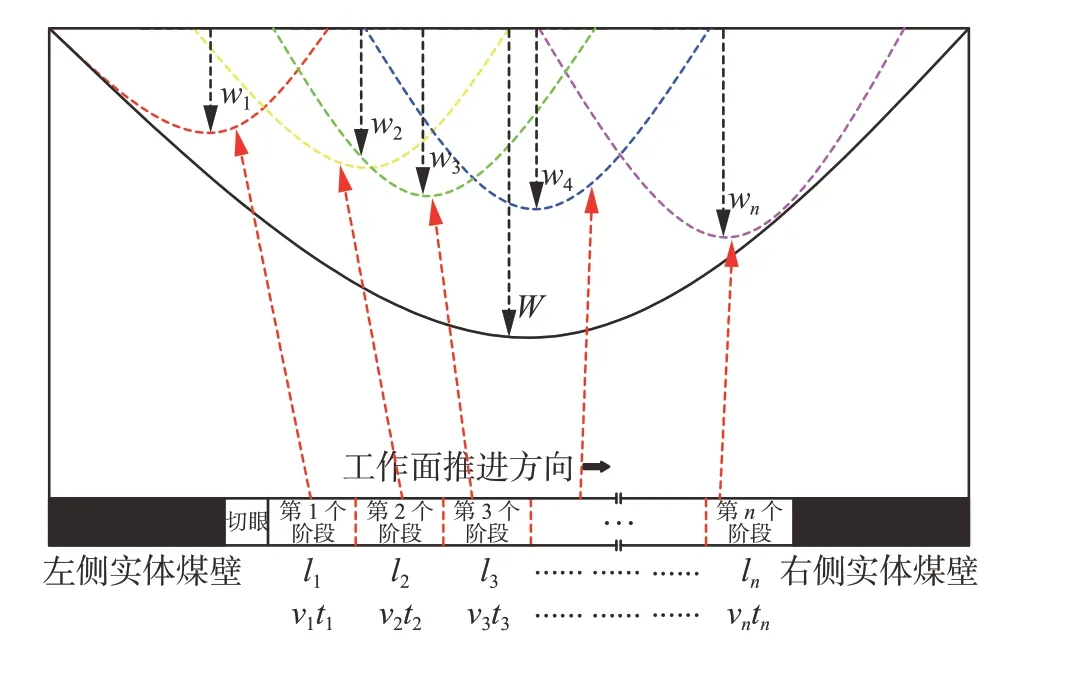
图1 走向主断面沉陷原理分析图Fig.1 Principle analysis diagram of strike main section settlement
假设工作面开采预计时间为t,即工作面从开切眼推进之日起,到工作面开采结束的时间差值;l为工作面开采长度,单位m;v为工作面推进速度,单位m/d。若有tv≥l,则表示工作面内所有单元都参与地表下沉过程;若有tv 由概率积分法预测[18]可知,开采沉陷为阶段累积变化过程,对于如图1 的单一长壁式工作面开采的过程,可以将工作面按照推进过程划分为n个单元:则对于第1 个阶段,假设工作面推进速度为v1,工作面单元沉陷预计时间为t1,即有:l1=v1t1;对于第2 个阶段则有l2=v2t2;可知第n个开采阶段,工作面的推进距离有ln=vntn,而各个阶段之间的持续时间为相邻之间的差值,则第1 个单元一直持续到第n个单元地表下沉的持续时间为: 则开采第1 个单元体的动态下沉值为: 第2 个开采单元的动态下沉值为: 则开采至第n个单元的动态下沉值为: 对于预计时刻,地表走向累积动态下沉W(x,t)为: W(x)概率积分法计算公式为: 式中:r为走向开采影响半径,m。 同理可知,倾向累积动态下沉W(y,t)为: W(y)概率积分法计算公式为: 式中:R为倾向开采影响半径。 Usher 模型为描述增长信息随时间变化的模型[19],其微分方程表达式为: 式中:z为模型函数;a为变化增长因子;b为形状因子(取值范围为0~1);zm为极限值,又称最值。 式(12)经过变形积分后得到用于表示采空区地表动态沉陷预测的函数,其表达式为: 式中:W(t)为t时刻地表的沉陷量;c为沉陷参数;a为时间系数;b为下沉曲线形状控制参数。 对式(14)进行求导得: 而对于单点的下沉速度即为2 点下沉值和时间差值的比值,则有: 将式(16)代入式(15)可得下沉速度与时间的函数v(t)为: 而由《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采指南》一书中可知,地表动态下沉时间函数积分W(x,y)t为[20]: 则引申出地表走向动态下沉函数W(x,t)为: 引申出地表倾向动态下沉函数W(y,t)为: 将式(8)、式(17)代入式(19)得: 同理将式(11)、式(17)代入式(20)得: 1)工作面概况。研究矿井的工作面开采4#煤,埋深为234 m,采高为4.0 m,倾角为2°,煤层产状由终采线向切眼方向倾斜,煤层为南北走向,设计倾向长为200 m,走向长为1 200 m。回采结束后采空区实际倾向长为195 m,走向长为1 157 m。 2)观测站布置情况。研究中采用十字交叉法布置测线,观测线布置图如图2。共布设2 条观测线,1 条为沿工作面倾向观测线(C-D),长度为850 m;1 条为沿工作面走向观测线(A-B),长度为1 050 m,该观测线从采空区的外侧开始,直至工作面内部。同时在观测线上按一定的方法要求布设若干个观测点,测点之间间距为20 m。 在确定坐标的前提下,以多次观测得出的数据进行计算分析。从2021 年2 月观测站建成起,至2021 年12 月共进行14 次监测,观测间隔平均约为21 d。 为了获得由于工作面开采而导致得地表移动下沉的清晰展示,使用FLAC3D数值模拟软件,以某煤矿工程地质条件为模拟基础,建立立体,模型整体图,模型如图3。设计模型尺寸为500 m×1 000 m×300 m 模型采用Moore-Coulomb criterion模型。模型除顶部外其他7 个面固定。模型上部施加0.16 MPa 模型各岩性参数见表1。 表1 岩性参数表Table 1 Table of lithology parameters 图3 模型整体图Fig.3 Overall model 走向下沉模拟图如图4。 图4 走向下沉模拟图Fig.4 Simulation of subsidence 由图4 可以看出,工作面推进200 m 时地表表现为隆起,且隆起值为649 mm,当推进至400 m 时由于工作面上覆岩层向采空区的垮落而表现为沉陷,此时地表隆起值减小至500 mm,于是得出随着工作面的推进,地表下沉值沿着走向不断增大,且在开采初期表现为地表隆起现象。由“砌体梁”理论可知,工作面开采后采空区内侧随工作面的推进而向下破断形成“倒三角”下沉堆叠,由于应力的集中,使得采空区外侧对应地表位置发生局部隆起[21]。在工作面开采中期即工作面推进至600 m 范围内地表沉陷值急剧增大,由原本的隆起500 mm 左右,变为下沉2 840 mm,并且达到最大地表沉陷,此时工作面达到充分采动。之后的开采过程中工作面下沉速度减缓,直到工作面推进至950 m 即开采结束,地表仍旧发生缓慢下沉,表现为残余下沉。 非充分开采阶段走向下沉形状表现为“V”形下窄上宽,且“V”形底随工作面走向推进移动。充分开采阶段走向下沉形状表现为“U”形下平上宽,且“U”形底位置不随工作面走向推进而发生移动。 倾向下沉模拟图如图5。 图5 倾向下沉模拟图Fig.5 Tendency subsidence simulation diagram 由图5 可以看出,倾向下沉在工作面推进400 m 以内表现出与走向下沉相同的性质,但地表隆起值比走向大80 mm 左右,当工作面推进至600 m 时地表表现为下沉,且下沉值为2 035 mm。下沉曲线表现出“V”形,随工作面推进至950 m时地表倾向下沉达到最大值2 507 mm,其倾向下沉规律表现为:工作面推进200~400 m 时地表隆起降低,工作面推进400~600 m 时地表由隆起转为沉陷且下沉速度激增,工作面推进600~950 m时地表沉陷值处于缓慢增长。 根据观测站观测数据,确定走向Wmax=2 848.094 3 mm,r=450.675 3 m。代入式(21)进行拟合求得参数a=0.075,b=0.859,c=2 040 000。故走向动态预测下沉函数为: 根据式(23)由Origin 作出的走向下沉预测曲线如图6。 图6 走向动态下沉预测图Fig.6 Strike dynamic subsidence prediction 根据观测站观测数据,确定倾向Wmax=2 664.753 mm,R=390.245 3 m。代入式(22)进行拟合求得参数a=0.065,b=0.653,c=2 032 000。故倾向动态预测下沉函数为: 根据式(24)由Origin 作出的倾向下沉预测曲线如图7。 图7 倾向动态下沉预测图Fig.7 Prediction of tendency dynamic subsidence 采用数值模拟结果绘制的下沉曲线与实际曲线有一定的区别,从图中可明显发现,模拟下沉图较实际测量曲线图值偏低。说明模拟过程中地表移动条件对真实的地层反映具有不完善性。但是在验证预测函数的准确性时具有一定的参考性。 经过对走向、倾向预测函数进行的图绘分析,结果表明该预测函数能够准确地对走向以及倾向动态下沉进行精准定位,并且能够有效地对下沉过程进行动态反映。 1)以Knothe 时间函数为基准,结合概率积分法做过程演化,最后联立Usher 函数进行推导,分别得到了走向、倾向动态下沉预测函数模型。 2)通过使用FLAC3D数值模拟软件构建模型,得到了工作面开采动态下沉规律:开采初期,地表表现为隆起,且隆起量为 600 mm 左右;开采中期,地表表现为下沉,且在工作面推进距离为 600 m 时达到充分采动,此时下沉值为 2 850 mm,地表沉陷形状表现为“U”型。 3)对预测函数进行参数拟合,得到了走向、倾向动态下沉值预测公式。并通过对公式进行绘图与地表下沉模拟曲线、实测曲线对比分析结果显示相似度很高,验证了走向、倾向动态下沉预测公式的准确性。 4)通过对该公式的使用,能够有效地对由于工作面充分开采而引发的地表下沉做出1 个动态的结果预测,进而有助于对地表建筑物等采取防护措施,对工作面是否需要采用充填开采方案做出判定。2 基于Usher 函数对动态下沉模型的构建
3 工作面及观测站概况
4 数值模拟
4.1 模型构建
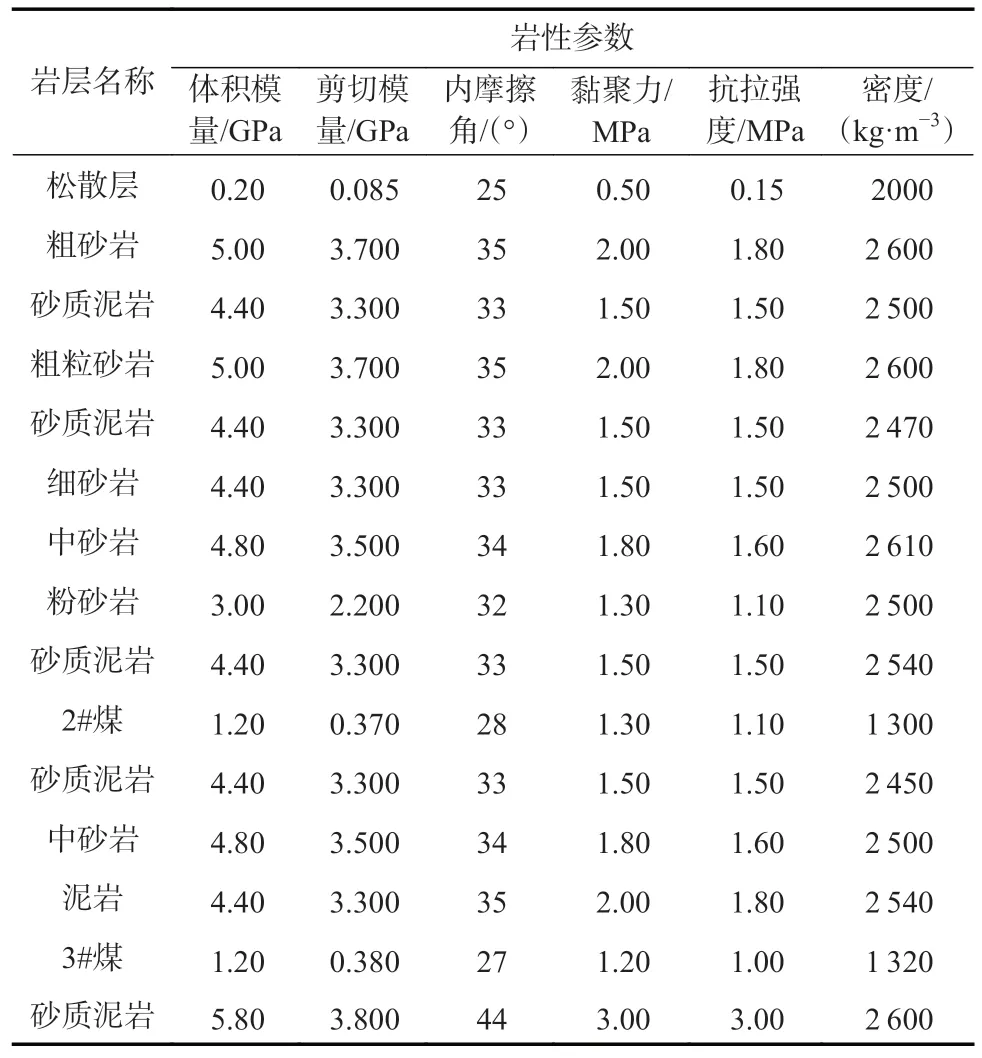
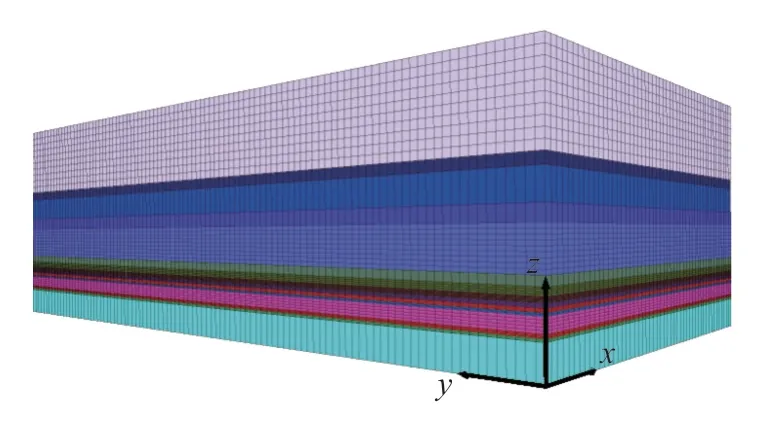
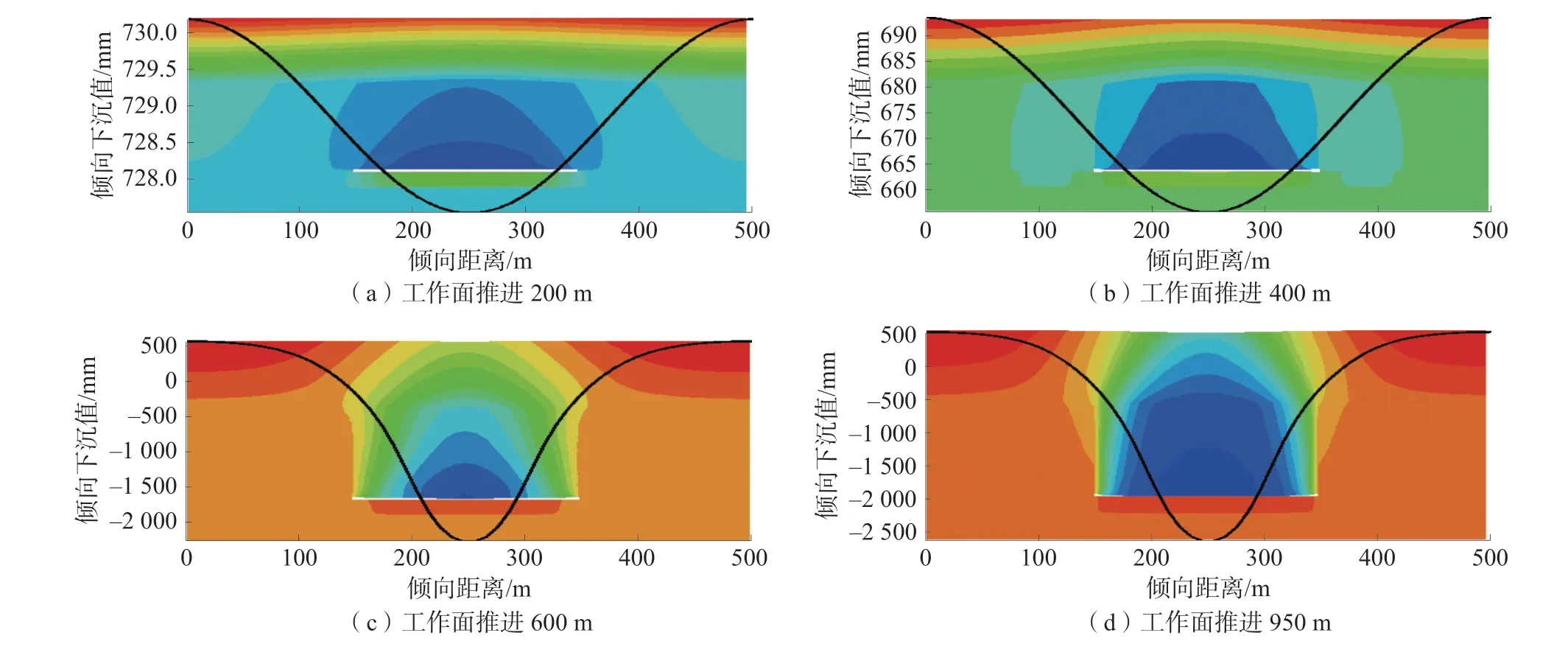
4.2 走向下沉
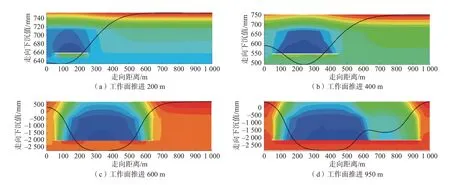
4.3 倾向下沉
5 地表移动动态下沉值预测
5.1 走向动态下沉预测
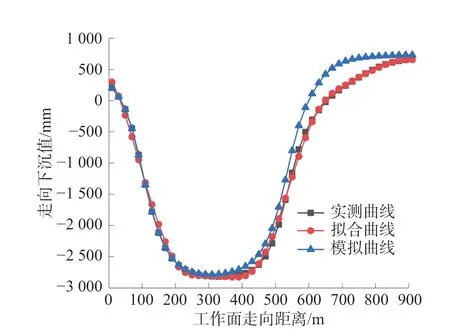
5.2 倾向动态下沉预测
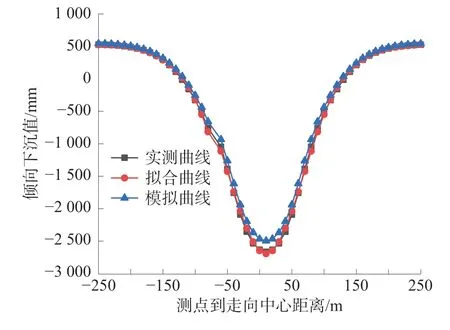
5.3 结果分析
6 结 语

