相交弦中点所在直线过定点问题探究
马宏酉 魏东升
(福建省厦门双十中学漳州校区,福建 厦门 363107)
魏东升(1985.4-),男,江西省瑞金人,本科,从事高中数学教学研究.
本文用三种方法剖析了一道椭圆中两条相交弦中点过定点的问题,一是求出中点坐标,利用这两点建立直线方程,从而求出定点;二是设中点所在的直线方程,将两个中点坐标代入,相减之后得出参数之间的关系,进而求出定点;三是不用联立,直接斜率坐标化,从而求出定点.
1 两相交弦的交点在坐标轴上
例1已知圆A:(x+1)2+y2=16,B(1,0),M为圆A上任意一点,线段BM的垂直平分线交AM于点N,点N的轨迹为W.
(1)求轨迹W的方程;
(2)过点B(1,0)的直线l1,l2的斜率分别为k1,k2,k1+k2=-1,l1交W于点C,D,l2交W于点E,F,线段CD与EF的中点分别是点G,H,判断直线GH是否过定点,若过定点,求出该定点,若不过定点,说明理由.

(2)方法1 (直接法)由题意设直线l1,l2的方程分别是y=k1(x-1),y=k2(x-1).
设C(x1,y1),D(x2,y2),






所以直线GH的方程为
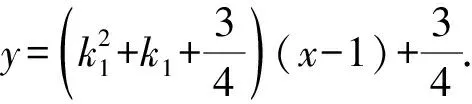

方法2 (作差法)由题意设直线l1,l2的方程分别是y=k1(x-1),y=k2(x-1).

设GH所在直线方程为y=kx+b,则
①
②
由①-②,得-3(k1-k2)=4k(k1+k2)·(k1-k2)+4b(k1+k2)·(k1-k2).
由于k1≠k2,所以-3=4k(k1+k2)+4b(k1+k2).




③
④



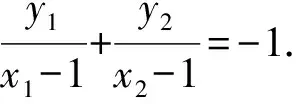

即3x1-3x1·x2+4y1·y2=-4x2y1+4y1.⑤
3x2-3x1·x2+4y1·y2=-4x1y2+4y2.⑥
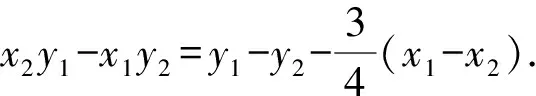
所以GH所在直线方程为

2 两相交弦的交点不在坐标轴上
变式1 已知圆A:(x+1)2+y2=16,M为圆A上任意一点,线段BM的垂直平分线交AM于点N,点N的轨迹为W.
(1)求轨迹W的方程;
(2)过点B(1,1)的直线l1,l2的斜率分别为k1,k2,k1+k2=-1,l1交W于点C,D,l2交W于点E,F,线段CD与EF的中点分别是G,H,判断直线GH是否过定点,若过定点,求出该定点,若不过定点,说明理由.
解法1 (作差法)由题意设直线l1,l2的方程分别是y=k1(x-1)+1,y=k2(x-1)+1.


设GH所在直线方程为y=kx+b,则
由⑦-⑧,得-3(k1-k2)=k[4(k1+k2)·(k1-k2)-4(k1-k2)]+4b(k1+k2)·(k1-k2).
又因为k1≠k2,所以
-3=4k(k1+k2)-4k+4b(k1+k2).
因为k1+k2=-1,所以4b=3-8k.


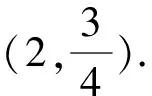

⑨
⑩





即4y1y2-8y2-3x1x2+3x2=-4x1y2.
同理 4y1y2-8y1-3x1x2+3x1=-4x2y1.
-8(y2-y1)+3(x2-x1)=-4(x1y2-x2y1).
所以GH所在直线方程为

3 两相交弦的交点坐标一般化
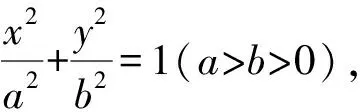
解法1 (作差法)设C(x1,y1),D(x2,y2).由题意,得直线l1方程为y=k1x+n-k1m,




设lGH:y=kx+φ,则

所以-mb2(k1-k2)=k[ma2(k1+k2)(k1-k2)-na2(k1-k2)]+a2φ(k1+k2)(k1-k2).
因为k1≠k2,k1+k2=t,则



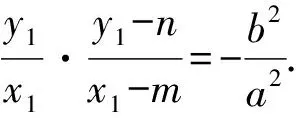
因为k1+k2=t,

即-b2x1x2+b2x1m+a2y1y2-a2y1n=ta2y1x2-tma2y1,
-b2x1x2+b2x2m+a2y1y2-a2y2n=ta2y2x1-tma2y2.
所以b2m(x1-x2)-a2n(y1-y2)=-tma2(y1-y2)+ta2(y1x2-y2x1).
所以GH所在直线方程为

4 性质类比到双曲线和抛物线


笛卡尔说过:“我所解决的每一个问题都将成为一个范例, 以用于解其他问题.”为了应对高考, 每天庞大的题量给学生的心理带来了很大的负担和压力, 给学生减负于我们而言责无旁贷. 因此, 我们只有跳进题海, 善于对同一类问题做深入的研究和总结, 做到触类旁通, 才能让学生跳出题海, 才能在解题时化难为易、化繁为简. 像对直线过定点这类问题进行解题教学时, 不仅可以让学生在解题中直接获益, 更可以培养其分析和解决问题的能力, 从而提升其数学的解题素养.

