利用导数研究恒成立问题的常见策略及其优化
展 佳
(江苏省沙溪高级中学,江苏 太仓 215400)
利用导数研究恒成立问题一直是高考的重点和难点.这类问题综合性非常强,往往涉及函数与方程(组)、不等式与等式、三角函数等多种知识,因此对于学生的思维要求非常高,运算强度大,解法也是多种多样.本文从学生最熟悉的参变量分离和含参讨论这两种方法出发,根据不同学生的思维情况提出了不同的解题建议,根据不同学生作业中反馈出的知识盲点与思路的断档处,提出一定的优化意见,促使学生学有所得、得有所想、反思内化,帮助学生提升数学学科素养,在考试中获得更好的表现.
1 典例赏析
题目已知函数f(x)=xlnx,当x≥1时,f(x)≤ax2-a恒成立,求a的取值范围.
1.1 参变量分离法
解析①当x=1,即0≤0,此时a∈R.


令h(x)=-x2lnx-lnx+x2-1,


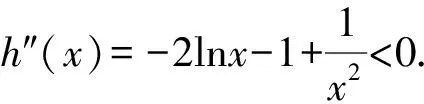
所以h′(x)在(1,+∞)单调递减.
所以h′(x) 即h(x)在(1,+∞)单调递减. 所以h(x) 即g′(x)<0. 所以g(x)在(1,+∞)单调递减. 反思此题参变量易分离,但分离后构造的新函数的导数相当复杂,需要多次求导方可达“彼岸”.这对于中等及偏下的学生是很不利的,经过1~2次导数运算,这些学生就丧失了解决此题的信心.那么,此题导数运算为何如此复杂?追根溯源,是因为x2lnx的存在.为了简化运算,可以考虑将lnx前的多项式全部除掉,对此笔者做了下面的优化. 即g′(x)<0. 下面求解过程同上,略. 分离参数是解决恒成立问题的一种重要解题方法,往往也是学生解题时优先考虑的方法,这个方法思维含量要求比较低,更具普适性.通过参数与主元的分离,达到以简驭繁的目的.但在使用的时候往往存在两个难点:一是参数与变量能否顺利分离,二是分离后得到的新函数的单调性以及最值能否顺利解决[1]. 解析原式等价于当x≥1时,xlnx-a(x2-1)≤0恒成立,求a的取值范围. 令g(x)=xlnx-a(x2-1),得 g(1)=0,g′(x)=lnx+1-2ax. 令h(x)=lnx+1-2ax,则 ①若a≤0时,得h′(x)>0. 则g′(x)在[1,+∞)上单调递增. 所以g′(x)≥g′(1)=1-2a≥0. 所以g(x)在[1,+∞)上单调递增. 所以g(x)≥g(1)=0. 从而xlnx-a(x2-1)≥0,不符合题意,舍. 即xlnx-a(x2-1)≤0恒成立. 反思对大部分高中生而言,分类讨论是难点,尤其是分类点的选择,此时可以通过抓住一些特殊点,比如利用端点值来缩小参数的取值范围,减少不必要的分类讨论情况. g′(x)=lnx+1-2ax, 令h(x)=lnx+1-2ax,则 即xlnx-a(x2-1)≤0恒成立 优化3由于g(1)=0,则g′(1)≤0. 令g(x)=xlnx-a(x2-1),得 g′(x)=lnx+1-2ax, g′(1)=1-2a≤0. 在含参讨论中运用端点效应常常起到事半功倍的效果.通过取函数定义域内的某个特殊的值或某几个特殊的值,先初步获得参数的一个较小范围即必要条件,再在该范围内讨论,或去验证其充分条件,进而解决问题,用该方法解决恒成立问题可以减少分类讨论的类别,但并不是所有恒成立问题均能通过端点效应解答[2],这只是一种优化手段. 解析显然a>0. 因为f′(x)=1+lnx,当x≥1时,f′(x)>0 ,所以y=f(x)在[1,+∞)单调递增且f(1)=0. 令g(x)=a(x2-1),函数g(x)图象开口向上,在[1,+∞)单调递增且g(1)=0. 运用数形结合法解决大题中的恒成立问题,由于对图象部分描述缺乏严格意义上的代数证明,或者说理不够清楚,在考试中存在扣分的现象,但对考生而言是能够降低思维成本、缩短思考时间、提高得分效率的,此方法更适合小题目. 恒成立问题的解题策略除了上述所介绍的,还有同构、放缩等,这些方法对于学生能力要求更高,题目的局限更大,考虑到所带班级情况,笔者在这里就不再一一展示.解决恒成立问题策略多样,这就要求教师在教学过程中一方面要关注学生的思维发展情况,真正做到因材施教,有针对性地进行教学点评,提出优化的建议,继而发展数学核心素养;另一方面要帮助学生认识到不同方法之间的差异在于对条件结论的认知区别,方法的选择依赖对条件结论和自身能力的判断.只有平时做好基础知识的储备和整理,方能在考试中大展拳脚.




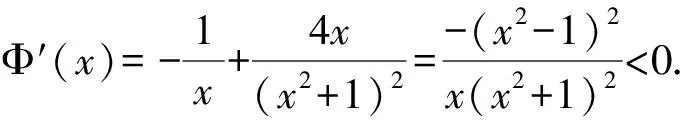

1.2 含参讨论法




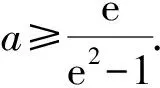








1.3 数形结合法

2 教学反思

