Zr55Al10Ni5Cu30非晶合金晶化相转变的价电子结构分析

2023-10-25 06:43刘伟东

材料科学与工艺 2023年5期

屈赫,刘伟东,屈华,杨松

(辽宁工业大学材料科学与工程学院,辽宁锦州 121001)

锆基非晶合金因具有玻璃形成能力大、强度高、硬度大等特点,受到广泛关注[1-3]。亚稳态非晶合金具有自发的物理老化趋势,即从高能量无序态向低能量有序态转变,发生相分离或晶化行为[4-6]。非晶合金的晶化主要有热致晶化、高压晶化、电致晶化、机械晶化等机制,其中等温退火法应用最为广泛[1]。目前,对于Zr-Al-Ni-Cu非晶合金的晶化行为,主要是基于热力学和动力学研究其晶化相的形核与长大及亚稳相向稳定相的转变过程。非晶合金Zr55Al10Ni5Cu30晶化过程分为亚稳晶化相形成和亚稳晶化相向稳定晶化相转变两个阶段,杨高林等[7]发现晶化初期形成的面心立方F-Zr2Ni晶化相在1 034 K附近转变为稳定的体心四方tI-Zr2Cu相;吴志方[8]发现亚稳晶化相为具有面心立方F-Zr2Ni结构的F-Zr2(Ni,Cu),之后亚稳相F-Zr2(Ni,Cu)转变为稳定的体心四方tI-Zr2Cu相。雷奕等[9]研究了Zr65Al7.5Ni10Cu17.5非晶合金的晶化相,发现晶化产物为稳定的tI-Zr2(Cu,Ni)相。晶化相的析出、转变及其尺寸、原子间的作用力对非晶合金硬度影响较大,胡欣怡等[10]发现非晶合金的硬度随着基体中析出的纳米晶数量的增加而增大,随着纳米晶尺寸的增大而降低。目前,对于非晶材料结构的研究主要还是从短程序(最近邻原子结构特征)分析入手,对于“隐含”的中程序,还停留在探索性描述阶段,基于现有实验手段难以精确表征其结构及演化、建立有效的结构性能关系,原子尺度的计算模拟是当前研究非晶材料结构及宏观物性与理论的重要手段[11-12]。非晶合金中的类共价键结合特征是其具有高模量和超高强度的主要原因,高模量可通过其电子结构特征来解释[13]。

余氏固体与分子经验电子理论(Empirical Electron Theory of Solids and Molecules,EET)[14-15]计算能够把原子中的电子分配到原子所形成的各条键上,所计算的能量也能够分配到各条键上,因此,合金性能-晶体结构-键能分布的关系较为容易建立,在处理复杂的实际多元合金体系问题时显得简便、实用,计算结果具有明确的物理意义,适合讨论多元合金体系。基于EET理论,本文计算并分析了晶化相F-Zr2Ni、F-Zr2(Ni,Cu)、tI-Zr2Cu、tI-Zr2(Cu,Ni)的价电子结构,从价电子结构层面阐释了亚稳晶化相向稳定相的转变过程。

1 晶化相的价电子结构计算

非晶合金中元素的分布从整体上看是均匀的,但因组成原子间的混合焓或成键能力的差异,局域分布是不均匀的[16]。Zr55Al10Ni5Cu30非晶合金经反复熔炼,从成分角度看,合金局部区域内Zr/Ni原子比远大于Zr/Cu原子比,且形成F-Zr2Ni相的驱动力要大于形成tI-Zr2Cu相[17],晶化初期优先析出F-Zr2Ni相,无法直接析出tI-Zr2Cu相。原子对间混合焓越负原子间的亲和力越大,Zr-Cu间的混合焓为-23 kJ/mol,而Al-Cu和Ni-Cu间的混合焓分别为-1和4 kJ/mol,且Cu原子的自扩散系数大于Ni、Al原子[18],在热激活条件下,Cu原子将会进入到F-Zr2Ni相中形成F-Zr2(Ni,Cu)相,为tI-Zr2Cu型晶化相的析出提供条件。

1.1 F-Zr2(Ni,Cu)相的价电子结构

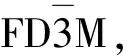
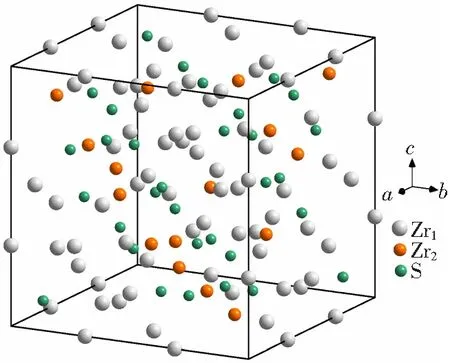
图1 F-Zr2(Ni,Cu)相结构模型

在1个F-Zr2(Ni,Cu)结构单元中,Zr原子因空间等效位置不同而分为Zr1和Zr2两种原子,S(Niy+Cux)原子只占据一种等效位置。Zr1原子点对称性为48f,其空间等效坐标位置为(0.311,0,0);Zr2原子点对称性为16c,其空间等效坐标位置为(0.125,0.125,0.125);S原子点对称性为32e,其空间等效坐标位置为(0.912,0.912,0.912)[20]。在1个F-Zr2(Ni,Cu)结构单元内有48个Zr1原子、16个Zr2原子和32个S原子。

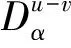
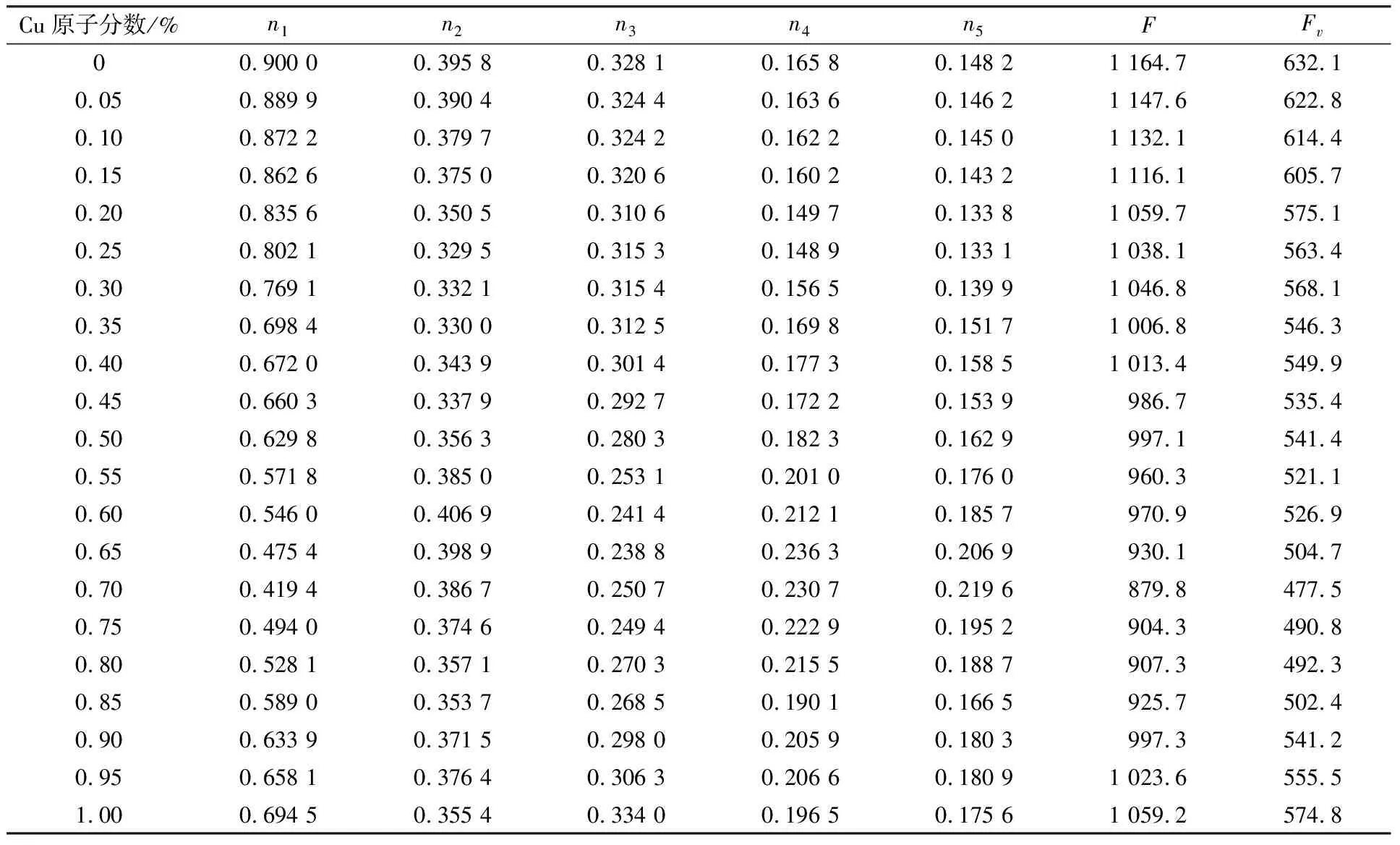
表1 F-Zr2(Ni,Cu)相的nα、F和Fv值的变化

(1)

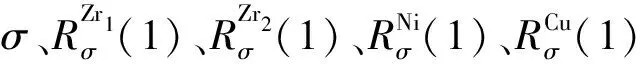
令rα′=nα′/n1(α′=2、3…6),则有

(2)

令∑nc为1个F-Zr2(Ni,Cu)结构单元中全部Zr1、Zr2、Ni和Cu原子于其σ杂阶上的共价电子数之和,则有

(3)

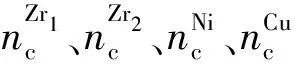
(4)

联立方程(1)与方程(2),可求F-Zr2(Ni,Cu)相各共价键上的共价电子数nα。将解出的nα代入键距方程(1),可得F-Zr2(Ni,Cu)的理论键距为

(5)

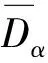
文献[21]中定义结构单元的总成键能力F=∑fαnαIα,单位体积成键能力Fv=F/v。其中fα为构成α键的两个原子的成键能力的算术平均值,v为晶胞的体积。F值越大,结构单元越稳定,越不容易改组重构。对于不同晶胞,体积差异较大时,应分析Fv值。nα表征了晶体结构单元中诸多原子所构成的共价键的结合力,nα值越大,键合力越大,组成原子更不容易移动[15]。F-Zr2(Ni,Cu)相的nα、F和Fv值的计算结果见表1。由表1可知,随着Cu原子分数的逐渐增加,所形成的F-Zr2(Ni,Cu)相的最强键共价电子对数n1、结构单元总成键能力F和单位体积成键能力Fv总体呈先减少后增加的趋势。当Cu原子分数为70%时,n1、F和Fv值达到最小值,即F-Zr2(Ni0.3,Cu0.7)相的原子间的键合力最弱,结构稳定性最差。

表2给出了F-Zr2(Ni0.3,Cu0.7)相的价电子结构,其中Zr1原子处于A种杂化第9阶,Zr2原子处于A种杂化第14阶,Ni原子处于A种杂化第7阶,Cu原子处于A种杂化第10阶。

表2 F-Zr2(Ni0.3,Cu0.7)相的价电子结构

1.2 tI-Zr2(Cu,Ni)相的价电子结构

tI-Zr2(Cu,Ni)相为体心四方结构,其结构模型如图2所示,空间群为I4/mmm,点阵常数为a=b=0.322 04 nm,c=1.118 32 nm[22]。tI-Zr2(Cu,Ni)相价电子结构的计算仍然采用EET理论平均原子模型,即采用平均原子S替代Cu和Ni原子,S原子含Cu原子分数y从100%逐渐减至0、含Ni原子分数x从0逐渐增至100 %,x%+y%=100%。在1个tI-Zr2(Cu,Ni)结构单元中具有4个Zr原子和2个S(Cuy+Nix)原子,Zr原子点对称性为4e,其空间等效坐标位置为(0,0,0.34);S原子点对称性为2a,其空间等效坐标位置为(0,0,0)[22]。

图2 tI-Zr2(Cu,Ni)相结构模型

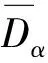
表3 tI-Zr2(Cu,Ni)相的nα、F和Fv值的变化

由表3可知,随着Ni原子分数的逐渐增加,所形成的tI-Zr2(Cu,Ni)相的最强键共价电子对数n1、结构单元总成键能力F和单位体积成键能力Fv总体呈先增加后减少的趋势。当Ni原子分数为40%时,tI-Zr2(Cu,Ni)相的n1、F和Fv值达到最大值,即tI-Zr2(Cu0.6,Ni0.4)相的原子间的键合力最强,结构稳定性最好。表4给出了tI-Zr2(Cu0.6,Ni0.4)相的价电子结构,其中Zr原子处于A种杂化第11阶,Cu原子处于A种杂化第13阶,Ni原子处于A种杂化第8阶。

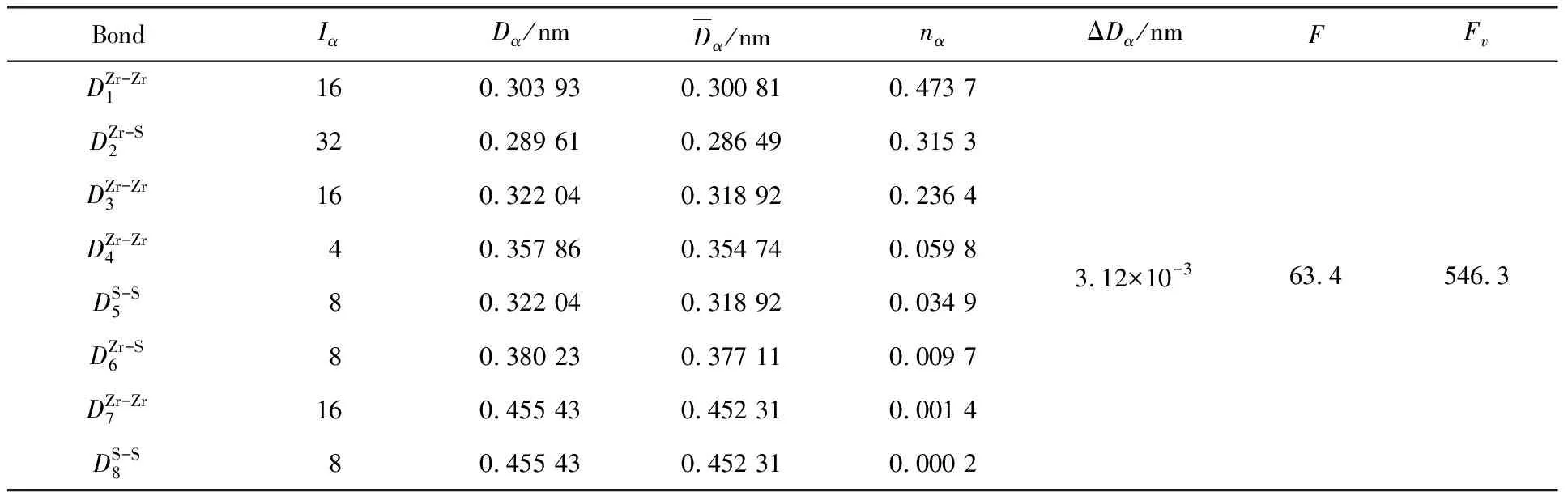
表4 tI-Zr2(Cu0.6,Ni0.4)相的价电子结构

2 晶化相价电子结构计算结果分析

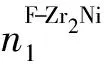
当F-Zr2(Ni0.3,Cu0.7)相发生分解时,局部区域内除了存在大量Zr、Cu原子外,还存在少量与Zr原子具有更大的亲和力的Ni原子,所以在加热条件下,亚稳相分解后应重构为稳定性更高的tI-Zr2(Cu,Ni)相,且结构中Cu原子的含量应高于Ni原子,以保持tI-Zr2Cu型晶化相的结构。

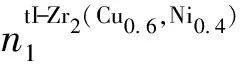
3 结论

1)F-Zr2Ni的原子间键合力远大于tI-Zr2Cu,F-Zr2Ni相的稳定性高于tI-Zr2Cu相;通过原子置换形成的F-Zr2(Ni0.3,Cu0.7)相的原子键合力最小、稳定性最差;F-Zr2(Ni0.3,Cu0.7)相的原子键合力略高于tI-Zr2Cu相,F-Zr2(Ni0.3,Cu0.7)相的稳定性略高于tI-Zr2Cu相,F-Zr2Ni相不易直接转变为tI-Zr2Cu相,F-Zr2(Ni,Cu)相不易分解重构为tI-Zr2Cu相。