基于Green函数法的受冲刷作用单桩横向动力学特性分析
马建军,韩书娟,高笑娟,李 达,郭 颖
(1. 河南科技大学 土木工程学院, 河南 洛阳 471023; 2. 河南省建筑安全与防护工程技术研究中心, 河南 洛阳 471023)
0 引言
桩基础作为一种经济有效的深基础形式,目前已广泛应用于工业建筑和民用住宅中[1]。已有研究表明,冲刷是导致桩基失效的重要原因,冲刷导致基床被移除,地基对桩基地支承和约束效应降低,可能导致上部结构坍塌[2]。LIN等[3]提出一种简化方法评估了冲刷孔尺寸对砂土中横向受荷桩响应的影响;ZHANG等[4]研究了应力历史、冲刷深度、冲刷宽度和冲刷孔坡角对软黏土中横向受荷桩响应的影响。
为满足桩基的水平承载需求,横向受荷桩的动力学研究已成为一个热点问题[5]。国内外学者对水平荷载下单桩的动力学特性进行了广泛研究,其理论模型可归为3类:连续介质理论、有限元或边界元和Winkler地基梁模型。利用连续介质模型,POULOS[6]分析了黏土中桩基在准静态循环荷载作用下的挠度,MILLN等[7]研究了简谐激励作用下桩基支撑结构的动力响应。基于动力 Winkler模型(BDWF),胡安峰等[8]得到了黏弹性地基中单桩动力响应的解析解。
对于复杂场地中的桩基,可采用多种方法研究其动力学特性,其中尤以数值方法最简便[9-10]。有限差分法的数学概念直观,便于编程,常用于弹性细长结构的数值模拟。利用有限差分方法,ANSARI等[11]求得Euler-Bernoulli梁的固有频率,BAO等[12]评估了土-结构相互作用对部分埋置单桩固有频率的影响。Green函数法的概念清晰,可得到系统动力响应的精确解,对于确定桩基的动态响应尤为重要。利用Green函数法,ABU-HILAL[13]求得Euler-Bernoulli梁的稳态解,LIANG等[14]分析了高承台桩基的动力阻抗和冲刷的影响。显然,将有限差分法和Green函数法相结合来分析桩基的固有频率和动力响应,将促进受冲刷作用部分埋置单桩动力学问题的求解。
基于横向受荷部分埋置单桩的动力学模型,本文利用有限差分法得到包含单桩控制方程的数值框架,冲刷过程中通过控制单元类型及数量实现对土-结构相互作用系统的准确建模,从而获得单桩更为准确的固有频率,分析冲刷作用对其横向动力学特性的影响;进而利用Green函数法,求得部分埋置单桩受迫振动的解析解,研究土体弹性模量、桩身长细比等对其横向动力响应的影响。
1 控制方程及其有限差分解
1.1 动力学模型
图1为部分埋置单桩建模分析的示意图。如图1所示,建立坐标系O-xyz,原点O位于未变形桩顶,x坐标沿横向激励方向设置,z坐标沿桩的轴线设置。为简便表述,基于以下假设:桩是细长、垂直和线弹性的;土场是均质、各向同性和线弹性材料;桩-土间的界面无滑移或脱离现象;忽略桩身在外激励方向之外的位移。
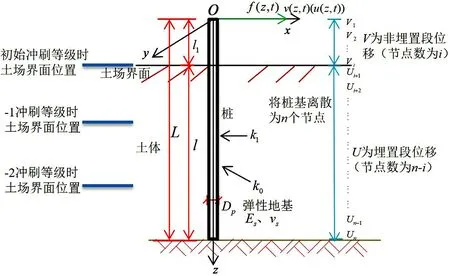
图1 横向受荷部分埋置单桩示意图Fig. 1 Sketch map of the laterally loaded partially-embedded single pile
根据单桩的埋置特征,忽略所有非线性高阶、阻尼和外荷载项,其运动控制方程为[12]:
(1)
(2)
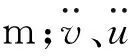
1.2 有限差分解
设式(1)和式(2)的通解为复数形式的y(z,t)和w(z,t),忽略外激励作用和阻尼,则取v(z,t)=Re{y(z,t)},u(z,t)=Re{w(z,t)}[13]。设式(1)和式(2)的通解分别为v=Vieωit和u=Ueiωit,其中ωi是桩基的第i阶频率,U和V分别为埋置段和非埋置段桩基的模态构型函数,将其代入式(1)和(2),可得
(3)
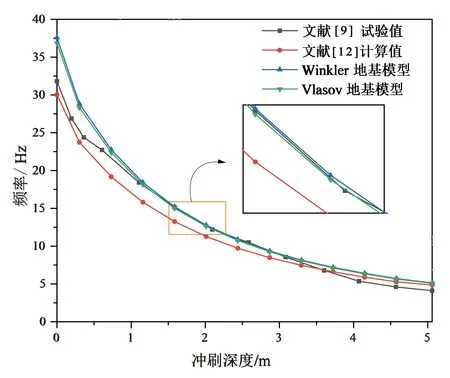
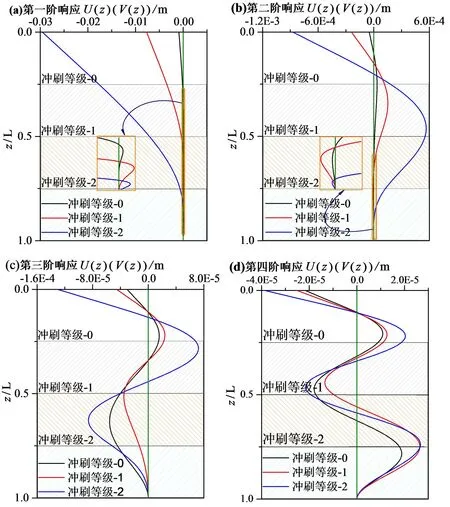
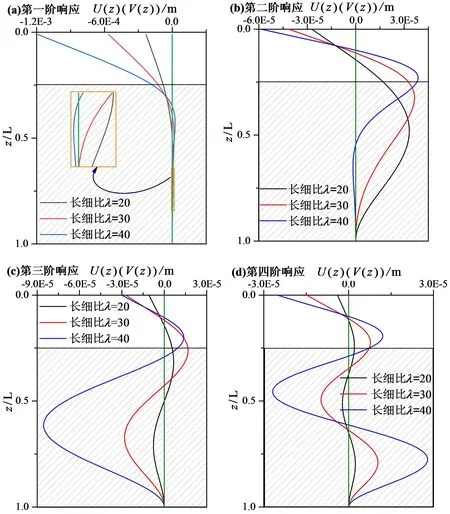
l1 (4) 以嵌岩桩为例,其边界条件为: (5) 离散式(3)和式(4),可得 (6) l1 (7) 式中:δz为用泰勒级数展开的模态构型的离散表达[15]。 进而,U的二阶和四阶导数可表述为 (8) 考虑虚节点Un+1、Un+2,由式(5)可得[11],当z=l时Un+1=0, 6Un-1+Un-2)/(12Δz)=0。 (9) 将式(8)和式(9)代入式(4),可得 (JB+ω2JD)Un=0, (10) 式中: Un=[Ui+1…Un]T, B=6+k0Δz4/(EI)+2k1Δz2/(EI), N=-4-k1Δz2/(EI), i为非埋置段节点数,n为桩基总节点数。式(10)等价于式(6)。 同时,由边界条件(5)可得,当z=0时, (11) 进而, J1+ω2JDVi=0, (12) 式中: Vi=[V1V2…Vi]T,D=-mΔz4/(EI)。 利用式(5)中的连续性条件,可得整个系统的对角矩阵 (E+ω2F)X=0, (13) 式中:X=[V1…ViUi+1…Un]T, F=diag(DD…D)。 令式(13)中E+ω2F的行列式为零,可得部分埋置单桩的各阶频率。 假设在z0处作用有简谐横向荷载 f(z,t)=δ(z-z0)F0eiΩt, (14) 式中:F0和Ω为外激励的幅值和频率,δ(·)是狄拉克函数。此时,式(2)中横向位移的解可设为 U(z,t)=U(z)eiΩt。 (15) 将式(14)和(15)代入式(2),得到 U(4)+a1U″+a2U=bF0δ(z-z0) , (16) 式中: 利用Green函数法,式(16)的解为 (17) 式中:f(z0)是外激励作用函数,G(z;z0)是待求的Green函数,且其为下式的解: U(4)+a1U″+a2U=bδ(z-z0)。 (18) 由式(18)可知,G(z;z0)=U(z;z0)。对式(18)中的变量z施行Laplace变换,可得 (s3+a1s)U(0)+(s2+a1)U′(0)+sU″(0)+U‴(0)), (19) 并记 sL=(s-s1)(s-s2)(s-s3)(s-s4), sG=s4+a1s2+a2。 利用文献[16],可得如下逆变换结果: A2(z-z0)b1+A3(z-z0)b1+A4(z-z0)b1), (20-a) (20-b) (20-c) A3(z)s3+A4(z)s4, (20-d) A3(z)+A4(z), (20-e) 式中:H(·)为单位阶跃函数,Ai(z)(i=1,2,3,4)为 (21) 由式(19)可知, (22) 将式(21)代入式(22)可得, G(z;z0)=H(z-z0)φ1(z-z0)+φ2(z)U(0)+ φ3(z)U′(0)+φ4(z)U″(0)+φ5(z)U‴(0), (23) 式中: (24) 因此,待定的Green函数G(z;z0)为 G(z;z0)=H(z-z0)φ1(z-z0)+ φ2(z)U(0)+φ3(z)U′(0)+ φ4(z)U″(0)+φ5(z)U‴(0)。 (25) 利用式(21)和式(24),可得 (26) 进而,可得 U(z;z0)=H(z-z0)φ1(z-z0)+ φ2(z)U(0)+φ3(z)U′(0)+ φ4(z)U″(0)+φ5(z)U‴(0), (27-a) (27-b) (27-c) (27-d) 将式(27)代入式(17),可得桩基的响应函数为 (28) 相应地,埋置段桩基的动力响应函数可表示为 U(z,t)=F0(H(z-z0)φ1(z-z0)+φ2(z)U(0)+φ3(z)U′(0)+φ4(z)U″(0)+φ5(z)U‴(0))cos(Ωt)。 (29) 如上节所示,式(1)可表示为 V(4)+κV=bF0δ(z-z0)。 (30) 显然,式(30)的解为 (31) 同理,对式(30)中的空间变量z施行Laplace变换及相应的逆变换,可以得到 (32) 式中: V(0)、V′(0)、V″(0)、V‴(0)是待定常数。 同理,由式(32)可得到 G(z;z0)=H(z-z0)ψ1(z-z0)+ψ2(z)V(0)+ψ3(z)V′(0)+ψ4(z)V″(0)+ψ5(z)V‴(0), (33) 式中: (34) 相应地,非埋置段桩基的动力响应函数为 V(z,t)=F0(H(z-z0)ψ1(z-z0)+ψ2(z)V(0)+ψ3(z)V′(0)+ψ4(z)V″(0)+ψ5(z)V‴(0))cos(Ωt)。 (35) 为验证有限差分法计算结果的准确性,分别采用PRENDERGAST等的计算模型[17]、Winkler 地基模型[18]和Vlasov地基模型[18],计算长度为8.76 m的环形钢桩的固有频率随冲刷程度变化的情况, 并与PRENDERGAST等现场测量结果对比[9]。 在冲刷条件下对桩基进行分析时,通过将其周围特定深度范围内土层完全清除至冲刷深度来模拟冲刷效应。将桩基离散为40个桩单元,冲刷深度以上不存在桩-土相互作用,看作梁单元;冲刷深度以下看作弹簧支撑梁单元。共设置3个冲刷等级,分别是初始地面高度(0冲刷等级)和2个冲刷深度(每个冲刷面相隔2.19 m),即:桩基总长为8.76 m,冲刷等级为 0时,非埋置段初始桩长为2.19 m,埋置深度为6.57 m,可表示为10个梁单元和30个弹簧支承梁单元;冲刷等级为-1、-2时,桩基埋置深度分别为4.38 m、2.19 m。利用自上而下移除弹簧支撑的方法模拟冲刷效应。 PRENDERGAST等的计算模型[17]为 Winkler模型[18]为 Vlasov模型[18]为 γ为衰减系数,可设为1。 桩和土体的物理参数如下:桩长L=8.76 m,外径R=0.17 m,内径r=0.157 m,密度ρ=7.8×103kg/m3,弹性模型E=2.0×105MPa,泊松比为ν=0.3;弹性地基(砂土)的泊松比为νs=0.3,设其单位重量为20 kN/m3,弹性模量为[12] (36) 式中:ρs为土体密度,νc为土体压缩波速度(砂土为213 m/s[12])。 图2给出了计算所得的频率与现场测量数据的对比[9]。随冲刷深度增加,利用Winkler模型求得的第一阶频率从37.576 Hz降至5.134 Hz,且在冲刷深度1~3 m间与实测值高度吻合。与Winkler模型相比,Vlasov模型考虑弹性地基的剪切效应,故求得的第一阶频率稍低于Winkler模型所得结果。总体而言,Winkler模型仅有一个地基反力参数,在工程中应用最广泛,且在常见的冲刷深度范围内,利用Winkler地基模型所得结果与实测值高度一致,故本文采用Winkler地基模型进行分析。 图2 有限差分法计算的第一阶频率与PRENDERGAST等测量结果对比Fig. 2 Comparison of the first-order frequencies calculated by the finite difference method with the result of the measurement by Prendergast et al. 为验证Green函数法求解桩基位移的正确性,计算文献[19]中桩径d=0.3 m,长细比λ=10,无量纲频率a0=0.3,单桩的位移曲线,并与文献[19]对比。图3给出了无量纲桩身位移U(z)/U(0)随埋置深度z的变化曲线。由图3可知,本文运用Green函数法所得计算结果与文献[19]基本一致,验证了该求解方法的正确性。 图3 Green函数法计算的桩身位移与文献[19]对比Fig. 3 Comparison of pile’s displacement calculated by Green’s functions method and literature [19] 本节研究冲刷作用对部分埋置单桩动力学特性的影响。利用3.1节中相关参数和式(36),可得地基弹性模量Es为67.41 MPa。桩端荷载为简谐横向荷载,令其幅值为F0为1000 N。 表1给出了部分埋置单桩前四阶频率随冲刷程度变化的情况,其中3个冲刷等级分别是0、-1和-2冲刷等级。由表1可知,单桩的各阶频率均随冲刷等级的增加而迅速减小,这是由于埋置土体的深度随冲刷进程不断减小,桩-土相互作用效应逐渐减弱。 表1 冲刷作用对单桩各阶频率的影响Tab. 1 Effect of scour on the frequencies of the single pile 图4为部分埋置单桩桩身前四阶响应随冲刷程度变化的情况。如图4所示,单桩各阶响应的桩顶横向位移均随冲刷等级的增加而增大,且桩身上部反弯点处的位移值也随冲刷程度的增加而显著增大。随冲刷程度加剧,桩周土场对桩基横向位移的约束迅速减弱,桩身侧向位移幅值显著增加。 图4 冲刷程度对单桩动力响应的影响Fig. 4 Effect of scour degree on dynamic response of the single pile 本节分析土体弹性模量对单桩横向动力学特性的影响。桩基埋置深度6.57 m,土体分别取:①松砂,Es1=10 MPa;②粉质砂土,Es2=20 MPa;③紧砂,Es3=50 MPa。地基的泊松比νs=0.3。 表2给出了部分埋置单桩前四阶频率随土体弹性模量变化的情况,其中土体弹性模量分别为10、20、50 MPa。可知,桩基的各阶频率均随参数Es的增大而增大。这里,弹性模量增大了1倍(4倍),桩基的第一阶频率增大了约20%(40%)。如3.1节所示,弹性地基反力系数值随土体弹性模量增加而增大,相应地桩周土场对桩基侧向约束作用加强。 表2 土体弹性模量对单桩各阶频率的影响Tab. 2 Effect of soil’s elastic modulus on the frequencies of the single pile 图5给出桩身各阶响应随土体弹性模量变化的情况。如图5所示,桩顶横向位移均随土层弹性模量增大而减小。相应地,桩身反弯点处的位移值也均随土体弹性模量的增加而显著减小。与表2所示结果相对应,随桩周土体弹性模量的增大,桩周土体对桩基的侧向约束增大,即桩-土相互作用效应增强,部分埋置单桩的横向变形减小。 图5 弹性模量对单桩动力响应的影响Fig. 5 Effect of elastic modulus on dynamic response of the single pile 桩身长细比λ简化为桩长与桩径的比值,即λ=l/Dp。通过改变桩径来改变参数λ,桩基的物理参数和弹性地基参数均保持不变。 表3给出了单桩在不同桩身长细比λ情况下的前四阶频率,其中λ分别取 20、30、40。由表3可知,随λ增大,第一阶频率减小,而高阶频率的变化规律则比较复杂。若λ增大了0.5倍(1倍),单桩的第一阶固有频率分别减小了约3%(10%)。 表3 长细比λ对单桩各阶频率的影响Tab. 3 Effect of slenderness λ on the frequencies of the single pile 图6为单桩各阶响应构型随桩身长细比变化的情况。桩基长细比越大,其刚度越小,越易发生屈曲和变形,故桩身的各阶响应构型均随桩身长细比的变化而发生显著改变。随长细比增大,桩顶横向位移增大,同时桩身反弯点位置上移。 图6 长细比λ对单桩动力响应的影响Fig. 6 Effect of slenderness λ on dynamic response of the single pile foundation 基于横向受荷桩的动力学模型,将有限差分法和Green函数法相结合,求得了受冲刷作用的单桩的各阶频率和动力响应构型,揭示了部分埋置桩基的横向动力学特性随冲刷作用变化情况。通过数值计算和参数分析,得到了以下主要结论: (1)随冲刷程度加剧,部分埋置单桩的各阶频率均显著降低,相应地各阶响应幅值明显增加。 (2)随土体弹性模量增大,桩基的各阶频率亦增大;若土体弹性模量增大了1倍(4倍),其第一阶频率约增大了20%(40%)。 (3)随桩身长细比增大,桩基的第一阶频率减小,若λ增大了0.5倍(1倍),单桩的第一阶固有频率分别减小了约3%(10%);而高阶频率的变化规律较为复杂,同时桩顶位移也显著增大。
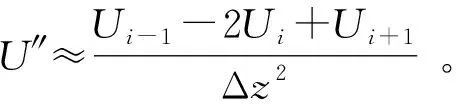
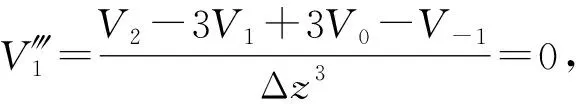
2 受迫振动的Green函数解
2.1 埋置段桩基


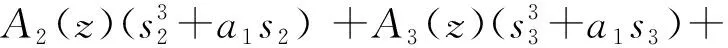



2.2 非埋置段桩基

3 数值计算
3.1 计算结果验证

3.2 冲刷作用分析

4 参数分析
4.1 土体参数


4.2 桩身长细比
5 结论

