面向多异构平台的不可压求解器的移植算法和优化
马文鹏,李瑞莹,袁 武,高凌云,翟环欣
(1. 信阳师范大学 计算机与信息技术学院, 河南 信阳 464000;2. 中国科学院 计算机网络信息中心, 北京 100083; 3. 中国科学院大学, 北京 100049)
0 引言
在工程计算领域,空气动力、航空航天、热能动力、天文物理等复杂流动问题大都可以采用计算流体力学(Computational Fluid Dynamics,CFD)的方法进行数值模拟,有效解决传统流体力学实验带来的巨大功耗问题。OpenFOAM(Open Source Field Operation and Manipulation,OpenFOAM)[1]是一个完全由C++编写的CFD软件,其前后处理功能强大、富含多种物理模型且版本更新快速,被广泛应用于各个工程领域。尤其近年来高性能计算(High Performance Computing,HPC)的迅速发展,为解决大规模工程实际问题提供了硬件支撑和有效的可编程实现手段,利用HPC强大的并行算力来提高OpenFOAM的性能已经成为主流趋势,愈来愈多的研究人员开始使用异构众核架构来改进CFD传统的数值计算方法。
VAN PHUC等[2]基于OpenFOAM对风场和自由面流场的模拟进行了多项研究,并使用日本超级计算机“京”成功生成了高达千亿单元网格的大规模瞬态CFD模拟,验证了千亿单元网格和数十万MPI(Message Passing Interface,MPI)的并行潜在能力。LIN等[3]针对OpenFOAM中的线性求解器提出了一种改进的预处理共轭梯度算法(Preconditioned Conjugate Gradient,PCG)和基于对角线的不完整Cholesky预处理器方法,在神威超算平台的单核组上分别实现了8.9倍和3.1倍的速度提升。REN等[4]提出3种减少通信操作的方案对PCG算法进行优化,基于超级计算平台天河二号验证了OpenFOAM的通信优化性能,使大规模线性方程组迭代求解的效率显著提升。ROJEK等[5]提出一种与人工智能模块集成的稳态CFD数值模拟方法,基于OpenFOAM工具箱MixIT,实现了卷积神经网络监督学习算法在GPU异构计算平台上10倍左右的加速。吴家明等[6]基于PETSc(Portable, Extensible Toolkit for Scientific Computation,PETSc)改进线性方程组求解模块,并将其集成到OpenFOAM框架中,验证了基于新PETSc框架的线性方程组在百万级大网格规模下的并行效率。孙士丽等[7]基于OpenFOAM针对三体船连接桥自由落体入水砰击模型进行数值模拟,验证了数值计算方法的正确性以及三体船连接桥入水砰击压力特性和范围,为三体船结构强度评估与结构设计提供了数值基础。HE等[8]提出一种面向对象的辅助应用框架,分别对OpenFOAM的原始求解器和湍流模型实现了高效优化辅助设计。
近年来,除了研究OpenFOAM的数值模拟计算方法外,针对其在异构架构上的性能扩展研究也日益增多,但异构架构上的移植工作多着眼于多节点MPI通信集合的性能提升。有些学者将求解器中线性解法器模块作为重点,研究其在异构架构上的大规模并行效率和优化,或是设计应用接口模型为其在异构架构上的移植扩展提供辅助分析。目前,一个完整的求解器框架在CPU+GPU加速器异构计算平台上的并行方案仍然存在一些挑战。主要表现在:一是OpenFOAM完全由C++语言开发,且为了此软件开发和维护的灵活性,不断采用C++的最新且高级的语言特性,这会带来异构平台上编译器的兼容性问题;二是CPU+GPU的异构软硬件生态成多样的发展趋势,如NVIDIA的GPU硬件平台搭配计算统一设备架构(Compute Unified Device Architecture,CUDA)[9]、AMD的GPU搭配ROCm(Radeon Open Compute,ROCm)[10],给同一求解器或算法在不同异构平台上的移植和适配带来额外的成本;三是C++中封装层次较深,底层数据不可见,给异构移植时一些面向底层数据的优化带来困难。如应用程序使用Field类表示CFD中各种物理场,对应于面向过程语言中的一维或高维数组,这些数据结构被封装在底层,无法轻易进行结构数组(Array of Structures,AoS)、数组结构(Structure of Arrays,SoA)[11]方面的访存优化。另外,软件的迭代和更新,也给某些模块的移植提供了思路。如在2020年6月发布的OpenFOAM-v2006版本[12],在求解线性系统方面对接了PETSc软件,使得PETSc中丰富的基于Krylov子空间[3]的线性解法器可以用于OpenFOAM的求解中,其中矩阵数据类型和PETSc数据类型的转化接口也为其外接异构线性求解器提供了借鉴。
对于上述问题,本文重点针对OpenFOAM的Field类和lduMatrix类设计了适应异构平台的、可灵活操作底层数据的结构,并通过数据转换接口实现两种数据的转换;采用可移植异构计算接口HIP(Heterogeneous-Compute Interface for Portability)[10]完整实现了不可压求解器icoFoam在两类主流异构平台(NVIDIA和AMD)上的移植和性能分析;针对求解过程中产生的线性方程组,在异构平台上设计了LDU(Lower Diagonal Upper)格式到CSR(Compressed Sparse Row)格式[13]的转换方案,并耦合hipSPARSE和hipBLAS[14]实现了基于Krylov子空间方法的线性求解器。
1 控制方程和PISO算法介绍
icoFoam是OpenFOAM提供的用来求解不可压缩层流的求解器,其对应的控制方程为:
∇·U=0,
(1)
(2)
式中:U是速度矢量,p是压力,v是黏度系数。式(1)是连续性方程,式(2)是动量方程。
icoFoam在非结构网格上采用有限体积方法离散控制方程,使用PISO(Pressure Implicit with Splitting Operator,PISO)算法[15]在每个时间步内实现压力和速度的多次相互修正来获得下一个时间步的压力和速度。具体的流程如图1所示。

图1 PISO算法流程图Fig. 1 Flow chart of PISO algorithm
在当前时间步内,将t0时刻流场的压力初值p0和速度初值U0代入公式(2)中,PISO循环开始。首先数值求解动量方程得到预测速度Ur,然后使用压力来表示速度,将速度代入连续性方程即公式(1)中,得到压力泊松方程,由预测速度Ur求解该方程,得到压力pλ,继而根据新的压力pλ对速度进行修正,得到修正后的速度Uλ。如果在当前时间步内未达到预期的迭代次数,则将Uλ当作新的速度值Ur作为下一次迭代的初始速度,当满足迭代次数时,t0时刻的PISO循环结束,跳出当前时间步,进入下一时刻继续求解压力和速度的耦合,直至最后时刻,输出最终压力pt和速度Ut。
2 并行方案设计
为了兼容主流NVIDIA和AMD的异构计算平台,图2展示了本文利用可移植的异构并行编程模型HIP设计icoFoam异构求解器的整体方案。
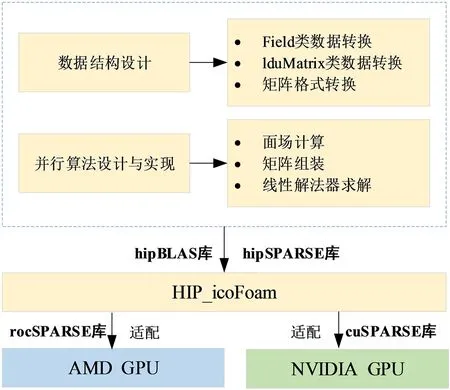
图2 整体方案设计Fig. 2 Overall scheme design
从数据操作的角度出发,将icoFoam的计算分为两大类:一类是关于物理场的操作,对应于Field类,如插值、通量计算、边界条件以及关于某个场数据的线性操作;另外一类是关于矩阵的操作,对应于lduMatrix类,如在矩阵组装成功后进行线性系统的求解,包括矩阵向量乘等。考虑到C++类对底层操作数据的封装性,通过设计对应的包含CPU端和GPU端数据的C结构,用于底层数据的优化。同时,设计了数据结构的转换接口,以保证异构计算之外的其他部分,如网格和流场数据的IO、流场数据的初始化工作、非结构网格拓扑相关计算操作均保留OpenFOAM的原始特性。
OpenFOAM-v2006版本首次利用其强大的二次开发功能和动态链接库机制对接了PETSc,使得外部丰富高效的Krylov子空间算法能够提供线性解法器。本文充分利用这一机制以及hipSPARSE支持多个后端异构平台的特性,设计了基于hipSPARSE的Krylov子空间方法的解法器,通过在数学库函数上层封装一层hipSPARSE的方式,使编译器hipcc在编译调用的数学库程序时,能够针对一套HIP程序在不同异构平台上链接对应的SPARSE库,如cuSPARSE或rocSPARSE[14]。
2.1 非结构网格数据结构转换
OpenFOAM中包含许多重要的类模板,考虑到类模板对底层操作数据的封装性,针对icoFoam求解器的Field和lduMatrix两种核心类,将程序的核心代码利用HIP编程模型重新实现,其余部分仍以C++为基础。
关于物理场的操作,其核心是对Field类的操作,如梯度计算、速度通量计算、边界条件以及关于某个场数据的线性操作,均是对Field类的操作。另外一类是关于矩阵的操作,对应于LduMatrix类,如对矩阵的组装、矩阵存储格式的转换以及矩阵组装成功后对线性系统的求解,包括矩阵向量乘等。Field和LduMatrix类都继承于List类,相当于对数组的操作,经过多层次的封装和继承,底层数据对用户均不可见,需要提取最底层的核心数据。因此基于HIP编程模型设计了数组结构的存储格式和数据接口用以底层数据的转换。如图3所示,以体场volFields类为例,设计同时包含CPU端和GPU端数据的结构以及数据转换接口,用于底层数据的转换,从而提高求解器的访存优化性能。

图3 Field类数据格式转换Fig. 3 Field class data format conversion
2.2 速度通量并行求解算法
Field类的核心工作是通过通量计算、插值计算和通量修正3个阶段实现对物理场phiHbyA的求解,最终返回1个面场,3个函数的共性是将网格格心数据插值为网格面数据。
如图4所示,OpenFOAM中通常将体场变量存储在网格格心,计算之前采用中心差分法将所有网格面对应的两个控制单元owner(简称O)和neighbour(简称N)的体场变量插值到面上。数据由体场到面场的操作中,每个网格面是独立的,由于网格的边界场数据不用进行插值操作,所以在计算过程中将内场和边界场分开处理,并组织与内面数量相等的线程数同时计算内场和边界场。
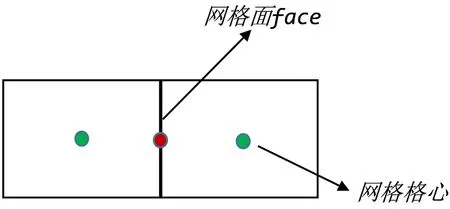
图4 网格格心数据的插值Fig. 4 Interpolation of grid cell center data
在线程组织方面,以网格内部面为单位来分配线程任务,假设网格内面的数量共有nIFaces个,那么有nIFaces个线程以blockSize的数量来分块,线程块数为「nIFaces/blockSize⎤个。在算法1中,由Vol表示体场,Sur表示面场,每个网格面上都有一个线程来实现内场和边界场上的体场计算面场的操作。
算法1:体场计算面场算法和并行实现
输入:Vol_U, Sur_Sf, 插值系数w, 所有网格面的O,N
输出:内场Sur_phii、边界场Sur_phib
1. tid← blockDim.x * blockIdx.x + threadIdx.x
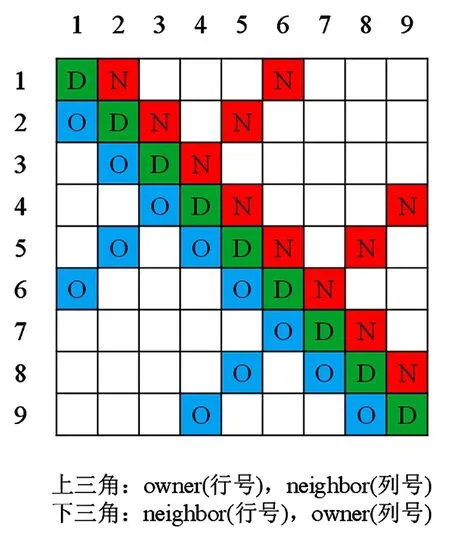
2. if tid 3. Sur_Ui[tid] ← w * (Vol_Ui[O[tid]] + Vol_Ui[N[tid]]) 4. Sur_phii[tid] ← Sur_Sfi[tid]Sur_Ui[tid] 5. endif 6. if tid 7. Sur_phib[tid] ← Sur_Sfb[tid] · Vol_Ub[tid] 8. endif 9. return Sur_phii, Sur_phib 如图5所示,Field类的矢量场在CPU中均采用典型的AoS模式来存储其空间上相邻的数据分量,例如x、y和z。这种顺序访存模式在GPU中导致访问单个类型变量时至少产生3倍的时间开销。因此计算过程中使用SoA结构将矢量场分量每一字段中所有的值存储到各自的数组中,使线程能够顺序且连续地访问数据,更高效地利用GPU的全局内存。 图5 AoS和SoA模式的内存布局Fig. 5 Memory layout for AoS and SoA patterns 如图6所示,OpenFOAM中的矩阵采用LDU的格式来存储线性方程组的矩阵系数:lower(简称l)、diag(简称d)和upper(简称u)分别对应下三角、对角线和上三角。其中,将网格内面对应的单元O和N代替行列索引upperAddr和lowerAddr作为矩阵上下2个三角元素的索引值共用的2个索引向量[8]。 图6 OpenFOAM中的矩阵存储格式Fig. 6 Matrix storage format in OpenFoam icoFoam求解器中,速度场和压力场对应的线性方程组信息分别存储在速度方程UEqn和压力方程PEqn中,离散后都会生成一个LDU格式的矩阵用于求解线性方程组。针对与速度方程UEqn相关的矩阵和源项组装,将其分为一阶时间导数项、对流项以及扩散项3个阶段。 一阶时间导数项中,基于网格单元求解对角线系数和源项;对流项和扩散项中,基于网格内面计算矩阵系数,基于网格单元计算边界贡献。因此依据网格特性来组织线程,例如以nIFaces个线程、「nIFaces/blockSize⎤个线程块同时计算矩阵系数和边界贡献。在计算对角线系数时,为了避免上、下三角系数取到同一个对角线的值而引起访问冲突,利用原子操作使读—计算—写能够连贯执行,确保只有当前线程访问计算对角线系数所需资源,不受其他线程干扰。 针对UEqn,设计算法2来组装矩阵系数和源项,pEqn中仅包含扩散项,UEqn中扩散项的组装方法同样适用于PEqn。 算法2:组装矩阵系数算法和并行实现 输入:1.网格体积C, 系数r, w, 速度Ut-1, 通量phi 输出:矩阵系数l, d, u、源项S、边界贡献Ic、Bc 1. tid← blockDim.x * blockIdx.x + threadIdx.x 2. if tid 3. d[tid] ← r * C[tid] 4. S[tid] ← r * Ut-1[tid] * C[tid] 5. endif 6. if tid 7. l[tid] ← w * phi[tid] 8. u[tid] ← l[tid] + phi[tid] 9. atomicAdd(&d[N[tid]],(-l[N[tid]]) 10. atomicAdd(&d[O[tid]],(-u[O[tid]]) 11. endif 12. if tid 13. Ic[tid]← 0.0 14. Bc[tid] ← phi[tid] * Ut-1[tid] 15. endif 16. return l, d, u, S, Ic, Bc OpenFOAM中关于流场的核心运算是通过网格面来组织的,如图6所示,其计算流程中线性系统的系数矩阵的存储格式也与面单元的拓扑结构一一对应。LDU格式的矩阵表示与以面为单位组织计算的特点非常契合,但是由于矩阵数据被拆分存储,也给在加速平台上矩阵按照整行(整列)为单位的操作(如稀疏矩阵向量乘操作)带来了不便,同时整行数据的分散存储阻碍了数据局部性、访存融合的优化。在加速平台上,提出了一种LDU到CSR格式的转换算法,且基于hipSPARSE库,针对速度方程和压力方程,耦合BiCGStab和PCG两种Krylov子空间方法作为线性系统的解法器。 算法3描述了该转换算法的过程,所有操作均在加速器上完成。 算法3:LDU格式到CSR格式的转换算法和并行实现 输入:LDU格式的矩阵上、下三角、对角数据: 1. u, l([0:nIFaces-1]), d([0:nCells-1]) 2. 所有网格面的O和N, ([0:nIFaces-1]) 输出:CSR格式的矩阵:csr_r, csr_c, csr_v 1. 将LDU格式合并成非排序的coo格式: tid← blockDim.x * blockIdx.x + threadIdx.x if tid (coo_r, coo_c, coo_v)[tid] ← (N, O, l)[tid] endif if tid (coo_r, coo_c, coo_v)[nIFaces+tid] ← (tid, tid, d[tid]) endif if tid nIFC ← nIFaces + nCells (coo_r, coo_c, coo_v)[tid + nIFC] ← (O, N ,u)[tid] endif 2.将Coo格式按照行压缩排序,得到置换P: P ← hipSparseXcooSortByRow(coo_r, coo_c) 3.将置换应用到coo_v得到排序后的矩阵: sorted_coo_v ← hipSparseDgthr(P, coo_v) 4.将coo_r按照行压缩存储得到csr_r: csr_r ← hipsparseXcoo2csr(coo_r) 5.csr_c ← coo_c; csr_v ← sorted_coo_v 6.return csr_r, csr_c, csr_v 算法3中,首先由LDU格式的存储规则,可以获得矩阵每个元素的行号和列号,发起一个kernel函数,将矩阵的下三角、上三角和对角元素的行号、列号及元素的值合并到一个未排序的COO格式存储的矩阵中;随后的任务就转化为将COO格式的矩阵按照行压缩进行排序,基于hipSPARSE库函数,此部分分为两个步骤:第一步是通过hipsparseXcooSortByRow获取一个从未排序到按行压缩排序的置换;第二步将置换应用到原始的COO格式的矩阵的元素中,得到转换过后的元素;最后,将COO格式表示的行信息coo_r压缩得到CSR格式表示的行信息csr_r。该算法最耗时的部分是得到置换数组P的过程,属于访存密集型操作,但是该步骤在针对由速度或者压力方程得到的系数矩阵时,只需要执行一次,因为在整个时间迭代过程中,每个时间步对应的系数矩阵非零元的位置是保持不变的。在得到CSR格式存储的矩阵之后,基于hipSPARSE和hipBLAS库,实现了Krylov子空间的PCG和BiCGStab两个线性解法器,用于求解压力和速度对应的线性系统。 实验是在分别包含AMD gfx906 GPU和NVIDIA TeslaV100 GPU的两个异构计算节点上进行的。其中,节点1采用的是2.5 GHz的CPU主频处理器,共有128 GB内存,并配置4块16 GB gfx906 GPU加速器,rocm版本为4.3(dtk 21.10)。节点2采用的是2.4 GHz的Intel(R) Xeon(R) E5-2640 v4 CPU主频处理器,共有128 GB内存,并配置4块16 GB的TeslaV100显卡,CUDA版本为10.0。 实验使用OpenFOAM-v2006版本的不可压缩层流顶盖驱动方腔流(Lid-driven Cavity Flow,Cavity)[1]为测试算例,如图7所示。该算例通过将z轴方向的边界条件设置为empty类型来实现二维的计算。 图7 Cavity算例模型Fig. 7 Example model of Cavity 针对Cavity算例在z轴方向进行扩展,将front和back的边界条件从原始的empty类型设置为symmetryPlane类型,movingWall与fixedWalls的边界条件保持不变,其网格控制文件blockMesh的设置如表1所示。 表1 Cavity中blockMesh设置Tab. 1 BlockMesh setting of Cavity 在使用Cavity算例测试时,同时将x、y和z轴方向扩展为20至40,60,…,100,设置算例运行时间为1×10-4s,时间步长为1×10-6s,共迭代100个时间步。在测试过程中关闭I/O操作,避免流场信息的频繁写入、写出影响测试结果的稳定性。 采用HIP实现的icoFoam的同一套不可压异构求解器,分别在ROCm和CUDA两个平台上进行测试。与2.2、2.3、2.4小节对应,在测试过程中分别统计这三部分在加速器上的时间,并与icoFoam在CPU上的时间进行对比分析。CPU版本的串行程序在编译过程中使用了-O3优化选项。为了保证对比实验的有效性,使用CPU最优的测试时间和GPU测试时间计算加速比,且为了避免测试的偶然性,统计测试时间使用连续3次在GPU上测试时间的平均值。 表2给出了不同网格规模下分别在ROCm和CUDA平台上面场相关操作的时间(tROCm、tCUDA)和对应的CPU上时间(tCPU)的对比。由表2的实验数据可以看出,经过100个时间步的迭代后,不同网格规模下的ROCm平台计算面场的算法加速效果在3.7~66.0倍。CUDA平台加速效果在5.4~87.2倍,随着网格规模的增大,加速比呈现递增趋势。说明与icoFoam串行计算相比,GPU的并行计算方法具有良好的加速效果,时间计算成本显著降低。 表2 面场串行和并行计算时间对比Tab. 2 Comparison of serial and parallel computation time of surface field 表3给出了不同网格规模下组装系数矩阵在各平台上的对比。根据表3的实验结果,发现GPU的矩阵组装并行方案加速效果明显,在ROCm计算平台上的加速比为2.6~43.3倍,CUDA计算平台上的加速比为5.4~66.4倍。值得注意的是,算法2在进行LDU格式矩阵系数组装时,使用了双精度原子操作,尽管如此,相比于CPU的时间,原子操作的实现依然有较大的并行优势,这主要得益于原子操作在两个平台上的高效实现。 表3 矩阵组装串行和并行计算时间对比Tab. 3 Comparison of serial and parallel computation time of matrix assembly 表4给出了算法3中从LDU格式到CSR格式的转换时间,由于在时间迭代过程中,两种格式在非零元位置的对应关系上保持不变,因此,算法3中得到置换的操作仅需要执行一次即可。表5和表6给出了分别使用PCG和BiCGStab求解一次压力和某个速度分量相关的线性系统的时间,虽然矩阵格式转换时间(20 ms左右)相比于求解一次线性系统的时间并不占优势,但是由于转换在整个求解流程中仅需一次,而每个时间步都需要求解一个线性系统,因此,矩阵转换时间相对于整个计算流程时间,如计算100个时间步,在1%左右,并不会影响整体计算效率。 表4 LDU格式到CSR格式的转换时间统计Tab. 4 Conversion time statistics of PCG algorithm LDU format to CSR format 表5和表6的实验结果表明,基于hipSPARSE和hipBLAS实现的两个Krylov子空间的线性解法器能够同时支持ROCm和CUDA平台,并能获得18倍和37倍的加速效果。由于求解线性系统占整个计算的大部分时间,因此对于icoFoam,整体在异构平台上的加速分别为20.5倍和38.4倍。 本文面向CPU+GPU众核处理器使用可移植性跨平台接口(HIP)实现了不可压缩求解器icoFoam在两类主流异构平台NVIDIA和AMD上的移植,基于异构众核加速器测试了不同算例规模下的求解器并行算法的计算时间。经过与OpenFOAM串行程序的对比分析,基于两类异构计算平台的整个求解器并行算法的设计,能够大幅度提升OpenFOAM的计算效率,大规模并行计算能力的提升分别高达20.5倍和38.4倍。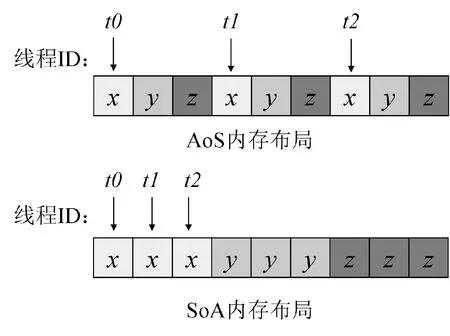
2.3 矩阵组装并行算法与实现
2.4 线性求解器并行算法与实现
3 测试环境及算例
3.1 测试环境
3.2 算例设置

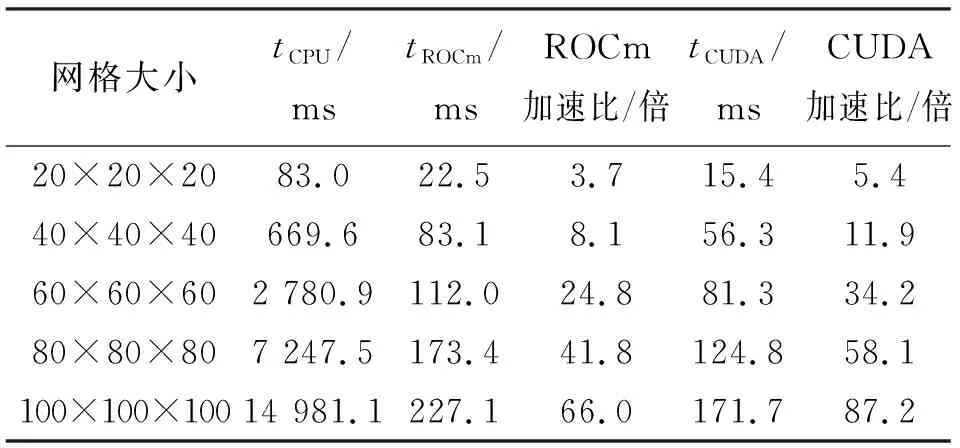
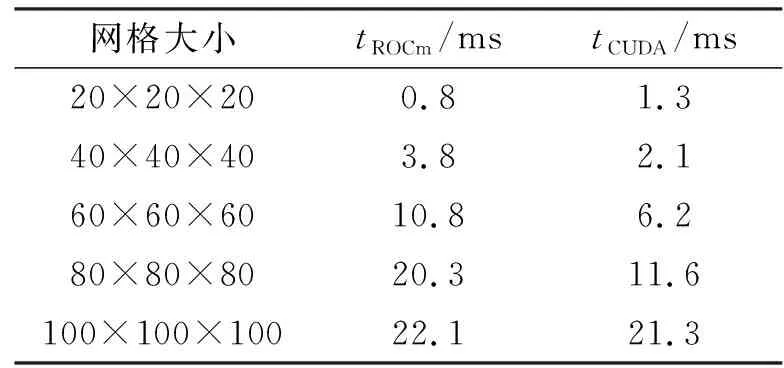
4 实验结果与分析

5 结论

