双金属复合管结构压弯承载性能试验研究

杨 璐，冈 毅，王法承，朱振兴

双金属复合管结构压弯承载性能试验研究

杨 璐1，冈 毅1，王法承2，朱振兴1

(1. 城市与工程安全减灾教育部重点实验室(北京工业大学)，北京 100124；2. 清华大学土木工程系，北京 100084)

为了研究双金属复合管的压弯承载性能，考虑试件偏心距和长细比这两个参数，对7个液压成型的X65/316L双金属复合管试件进行了试验研究．试验内容包括材性测试、几何初始缺陷3D扫描测量和压弯承载力试验．通过对比各试件的受力过程、破坏形态及数据结果，分析试件长细比和荷载偏心距对复合管压弯承载性能的影响．试验结果表明：试件在压弯荷载作用下的破坏模式为整体失稳破坏，试件达到极限荷载后具有良好的塑性变形能力．长细比越大，试件越容易发生失稳破坏，试件的弹性变形阶段越短，刚度和承载力均显著降低；而偏心距越大，试件承载力明显下降，试件刚度则略微降低．在此基础上，基于换算截面法对复合管截面进行等效换算，然后根据《钢结构设计标准》(GB50017—2017)中a类截面钢管的压弯失稳承载力公式计算复合管极限承载力，并将承载力试验结果与换算截面法计算值相比较．对比结果表明采用换算截面法考虑衬管的贡献计算得到的复合管压弯试件承载力与试验值吻合较好，平均误差小于10%且偏于安全．对比分析表明采用换算截面法设计双金属复合管能更好地考虑衬管的承载能力，研究成果可为此类构件在设计及相关工程的应用提供一定参考．

双金属复合管；压弯；承载性能；换算截面法；试验研究

双金属复合管通过塑性变形或其他的连接技术将外部基管和内部衬管复合成型[1]．复合管外部基管通常以碳素钢管为主，内部衬管多采用耐蚀合金管，使得复合管拥有良好的承载性能的同时还兼具着卓越的耐蚀性能[2-3]．复合管根据界面复合情况可分为机械式复合管[4]和冶金式复合管，由于工艺简单价格低廉目前机械式复合管使用较多．在管道的正常服役过程中，由于土体滑坡、温差效应、泊松效应、内压作用会使管道承受轴向压力，而地震、海底变形、滑坡和波浪冲击作用则会使海底管道处于受弯状态，因此复杂的海洋环境会对海底管道产生压弯作用，严重时会导致管道截面发生畸变，影响油气资源的运送．

目前针对双金属复合管构件的受力性能研究主要集中于轴压和弯曲等方面．在复合管轴压承载性能研究方面，Focke等[5]为研究复合管轴向压缩引起的衬管起皱问题，分别对衬管、位于基管内的衬管和复合管进行轴压试验．Bu等[6]对复合管轴压性能进行了试验研究，并用有限元法进行参数研究. Fathi[7]从理论和试验上，对耐腐蚀合金内衬在机械式复合的基管中由于轴向压缩而产生的局部屈曲行为进行研究．Peek等[8]提出了轴压作用下复合管轴对称起皱问题的分岔解析解，并利用有限元模型进行验证．在复合管受弯承载性能研究方面，Pépin等[9]研究了内压作用下复合管卷管铺设性能，进行了循环弯曲试验，以评估制造和循环塑性弯曲对衬管变形性能的影响．Tkaczyk等[10-13]对复合管进行了多循环塑性弯曲试验以模拟卷筒铺设安装，试验管道满足使用要求证明了公式的有效性．Focke[14]研究了复合管在卷曲过程中环焊缝对衬管完整性的影响.

综上所述，现有研究中缺乏对复合管压弯性能的研究，且目前工程中所采用的设计原则为基管满足设计允许应力而不考虑衬管的作用[15]，因此有必要对双金属复合管构件压弯性能进行研究，探索考虑衬管对承载力贡献的设计方法．本文分析了现有的相关文献，并在目前研究成果的基础上，对液压成型的机械式双金属复合管压弯构件进行压弯承载力试验，并将所求结果与承载力试验结果对比并进行分析．

1 试验概况

1.1 试件设计

试验所用的双金属复合管试件由液压成型工艺制作而成，图1[1]为双金属复合管结构示意图，双金属复合管机械复合工艺如图2所示．

图1 双金属复合管结构示意

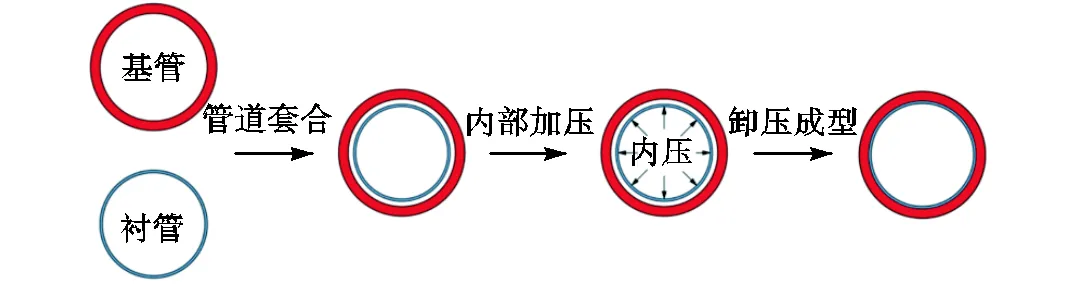
图2 双金属复合管机械复合工艺

为研究双金属复合管结构压弯承载性能，对7个双金属复合管长柱试件进行压弯试验．试件均采用相同截面尺寸，基管外径为168.3mm，壁厚1为12.7mm，衬管壁厚2为3mm．试件主要变化参数为荷载偏心距(70mm、100mm)和基管正则化长细比n(0.492、1.032、1.475)．试件长度按《钢结构设计标准》(GB50017—2017)[16]中的正则化长细比计算公式确定．试件的实测参数列于表1，表中e为试件两端铰接转动接触面间的距离，为有效长度．

1.2 初始缺陷测量

通过3D扫描得到试件表面形状．3D扫描装置为体积精度为0.02mm＋0.08mm/m的手持式3D扫描仪，试件制作前对每个试件进行3D扫描得到试件的三维模型，如图3所示．采用Geomagic软件处理模型得到试件的局部初始缺陷和整体初始缺陷．采用测量3D模型距管端100mm处的管道截面和跨中截面外径并计算不圆度[15]，将试件的三维模型与理想圆管进行比对得到试件的整体初始缺陷幅值，其值如表2所示，表中T、M、B分别为试件顶部、跨中、底部外径，为试件最大挠度．

表1 试件几何尺寸

Tab.1 Measured dimensions of the specimens

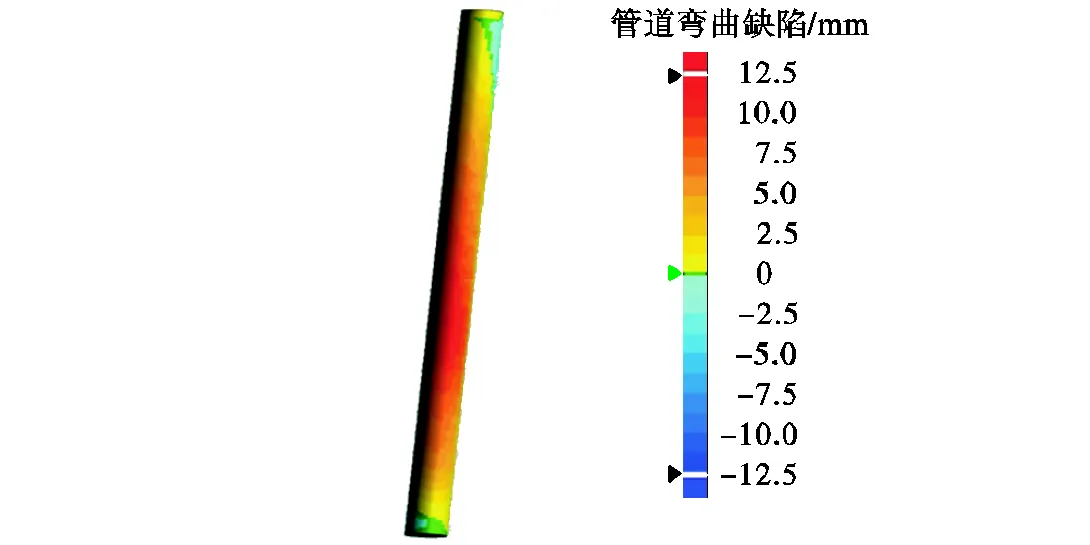
图3 3D扫描模型

表2 几何初始缺陷

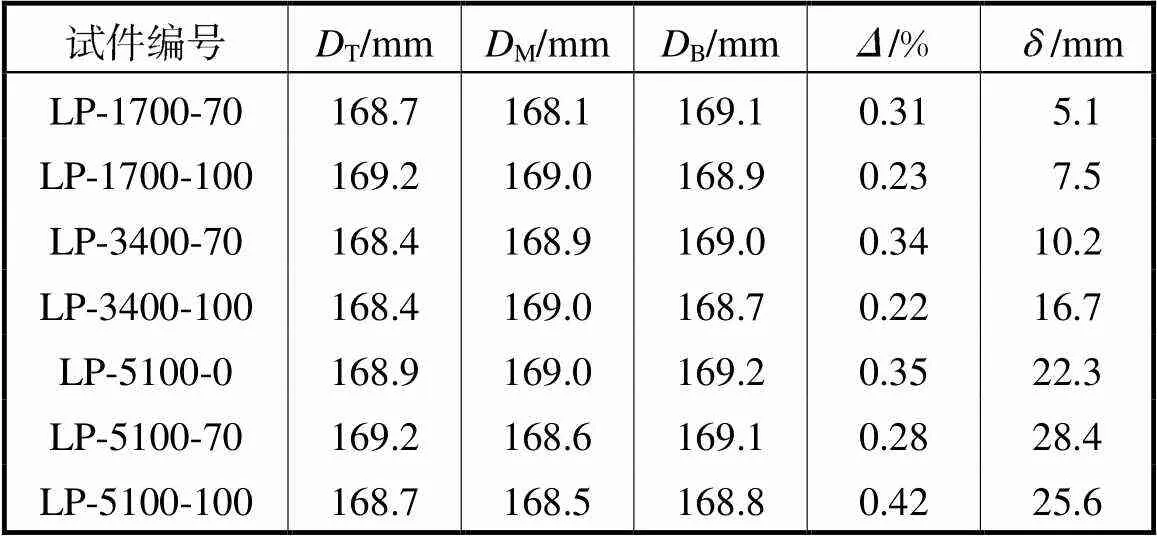
Tab.2 Initial geometric deficiencies

1.3 加载与测量方案

试验采用2000kN液压千斤顶进行加载，为减少重力对试验结果的影响，试件水平放置两端均采用单刀接支座．单刀铰刀口垂直放置，刀铰加载时可在水平面内旋转，试验装置如图4所示．在试件加载前进行对中、调平；安装完成后，对试件施加20kN的荷载进行预加载，检查试验仪器正常工作后，正式开始试验．

每个试件上共布置位移计8个，在试件加载端对称布置4个，中部布置2个，固定端布置2个，测点布置如图5(a)所示．试件中部布置的5号位移计用来测量跨中截面失稳平面内的水平位移，6号位移计用于测量试件的平面外位移．加载端的位移计，用于计算支座转角和试件的轴向变形．固定端的位移计，用于计算单刀铰转角．通过测量结果得到试件荷载-位移曲线．在复合管基管外侧跨中和两端共布置16个应变片，用于分析其受力状态与屈服程度．试件两端各布置4个轴向应变片，柱中布置8个应变片，其中包含轴向应变片4个(SG-5、SG-6、SG-7、SG-8)、环向应变片4个(SG-9、SG-10、SG-11、SG-12)，测点位置如图5(b)所示．

图4 试验装置

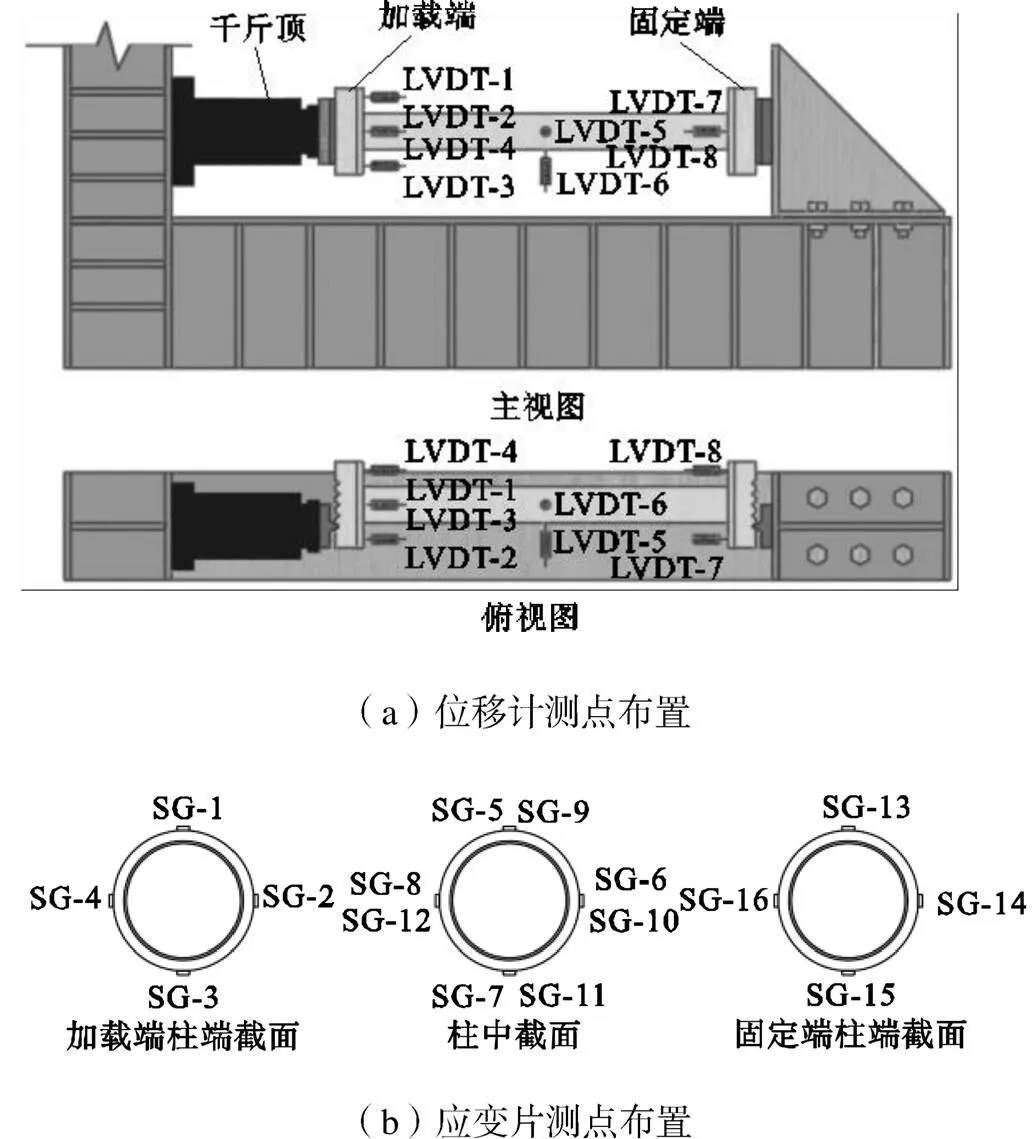
图5 测点布置

1.4 材性试验

分别对双金属复合管的基管和衬管截取试样，进行材性试验[6]．将试样通过特制夹具连接到试验装置上，复合管材料性能试验装置图[6]如图6所示．试样沿轴线在两端各开一个洞，采用设计的夹具夹持进行单调拉伸试验．双金属复合管材料性能指标[6]如表3所示，其中编号定义如下：O代表基管；I代表衬管；C表示用夹具进行夹持；0为初始弹性模量；0.2为残余应变为0.2%时的材料应力值；u为极限强度；f为断后伸长率．

图6 单调拉伸试验装置

表3 拉伸试验材料力学性能

Tab.3 Material properties of tensile coupon tests

2 试验结果及分析

2.1 试验过程及破坏形态

试验采用水平千斤顶进行加载，千斤顶最大推力为2000kN，行程为±300mm，试件加载方式为位移控制加载．开始正式加载前对试件进行预加载，预加载的荷载取20kN，为有限元试算的所有试件极限承载力的最小值的约5%，用以消除单刀铰与试件的空隙，以及查看应变仪、位移计等监测设备是否正常.试验过程中以1mm/min的位移增量匀速施加荷载.当试验试件发生较大变形后停止加载并进行卸载.

试件从开始加载至荷载达到极限承载力的70%左右时，试件产生的位移较小，发生的形变也并不明显．当试件加载到接近极限承载力时，随着轴向位移的不断增大，试件开始发生平面内的水平位移，单刀铰转角逐渐增大．在试件进入承载力下降阶段时，试件平面内的水平位移快速增长，同时试件跨中的水平位移增长速度加快，试件达到极限荷载后发生整体失稳破坏，试件承载力开始平稳下降．加载完成后试件的中部产生明显弯曲，左右两个单刀铰向试件压弯方向转动．而试验过程中试件的平面外位移在较小范围内变化，可以忽略不计，试件处于单向压弯作用．图7为试件破坏模式图，从试件的破坏模式可以看出试件发生整体失稳破坏．

图7 试件破坏模式

2.2 荷载-位移曲线

试件在压弯荷载作用下发生图8所示的整体失稳破坏，使试件产生轴向位移的同时产生较大的跨中挠度．试验得到3种长细比和2种荷载偏心距的双金属复合管压弯柱试件的荷载与位移关系曲线，如图9所示．复合管压弯构件荷载-位移关系曲线大致可分为弹性工作阶段、弹塑性工作阶段和塑性工作阶段．施加荷载较小时，试件处于弹性工作阶段，荷载与位移曲线线性正相关，受荷载偏心距和整体初始缺陷影响，跨中面内挠度有较小发展，且随试件初偏心距增加而扩大．随着施加的轴向位移的增大，试件中部的平面内位移增加速度明显加快，而试件荷载增长放缓，曲线不再是线性变化，此阶段为弹塑性工作阶段．达到极限荷载后，试件的面内位移快速增长，而荷载开始缓慢下降直至失稳破坏，此阶段为塑性工作阶段．由图9(a)可知试件长细比越大，刚度越小达到极限荷载时的面内位移越大．试件承载力与偏心距呈正比，与长细比呈负相关性．由图9(b)可知长细比小的试件相比长细比较大的试件在较小的轴向位移下更早达到极限承载力，长细比和荷载偏心距越大，试件达到承载力峰值时的轴向位移越大．

图8 压弯构件典型破坏形态

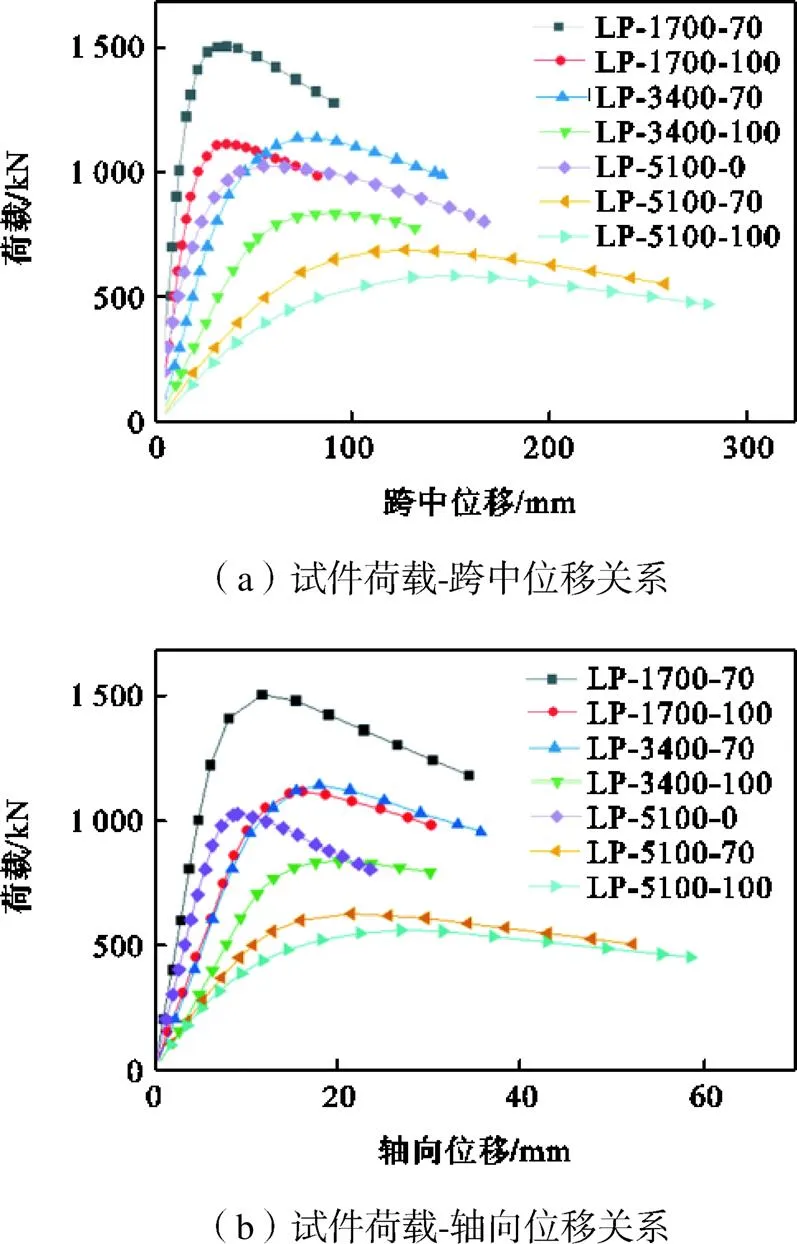
图9 试件荷载-位移关系

2.3 荷载-应变曲线

试验过程中，在试件中部位置共布置8片应变片，用于测量轴向和环向应变值，得到跨中受拉和受压两侧的应变变化．以试件LP-1700-70为例，其荷载-应变关系如图10所示．试件上下端应变片数值基本保持一致，说明试件仅在水平方向发生转动．试件受压侧和受拉侧应变值根据荷载偏心等比例变化，SG-8、SG-9、SG-10、SG-11应变片为正值，SG-5、SG-6、SG-7、SG-12应变片为负值，试件环向应变与轴向应变呈负相关，试件在受拉侧达到屈服后进入弹塑性发展阶段，达到极限承载力时试件受压侧和受拉侧均达到屈服应变．

图11所示为试件LP-1700-70、LP-1700-100、LP-3400-70、LP-5100-70跨中轴向拉压应变比较图．由于荷载形式为偏心受压，受压侧的纵向应变均大于受拉侧的应变．由图11(a)可知，偏心距大的试件弹性段刚度更小，承载力达到最大时应变值更小，下降段更加平缓，表现出较好的塑性发展能力．由图11(b)可知，试件达到极限承载力时，试件受压与受拉侧均发生屈服，但长细比大的试件应变值更小，更快表现出荷载与应变的非线性增长，试件更容易发生弹性失稳．

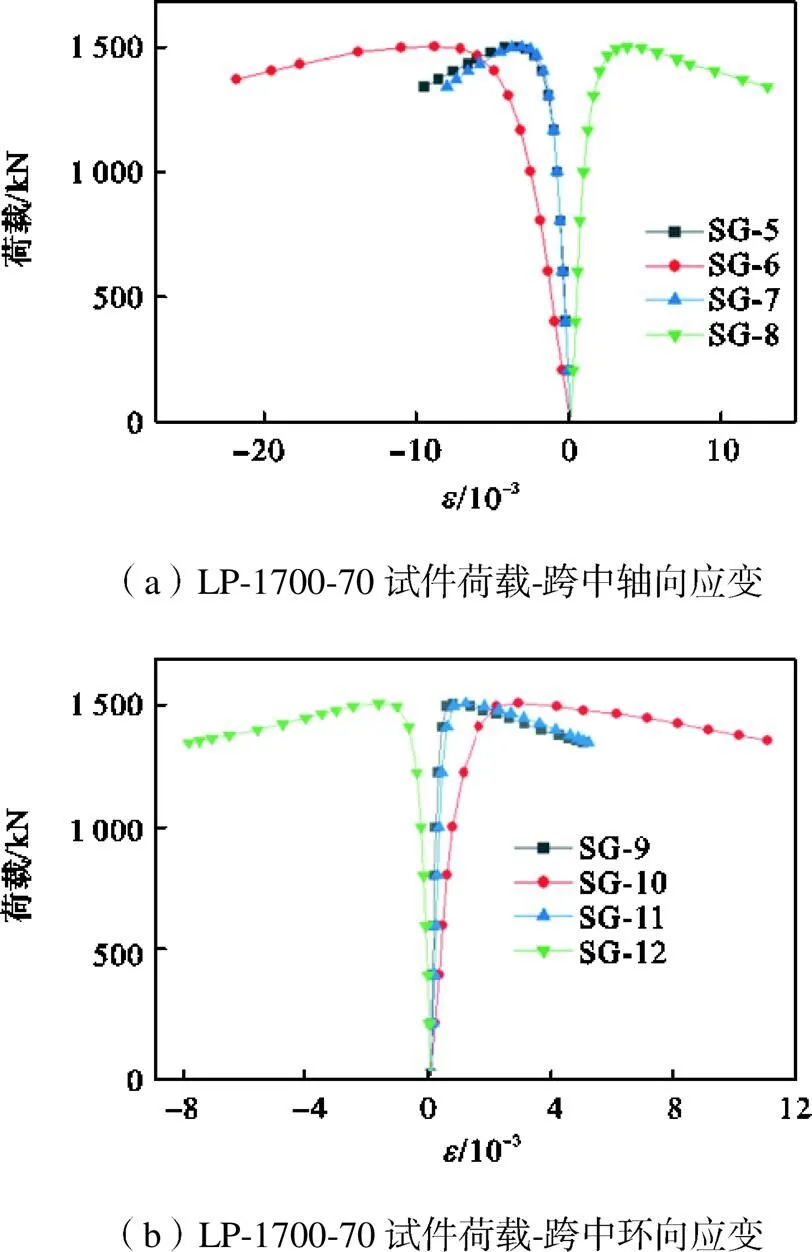
图10 LP-1700-70试件荷载-应变关系

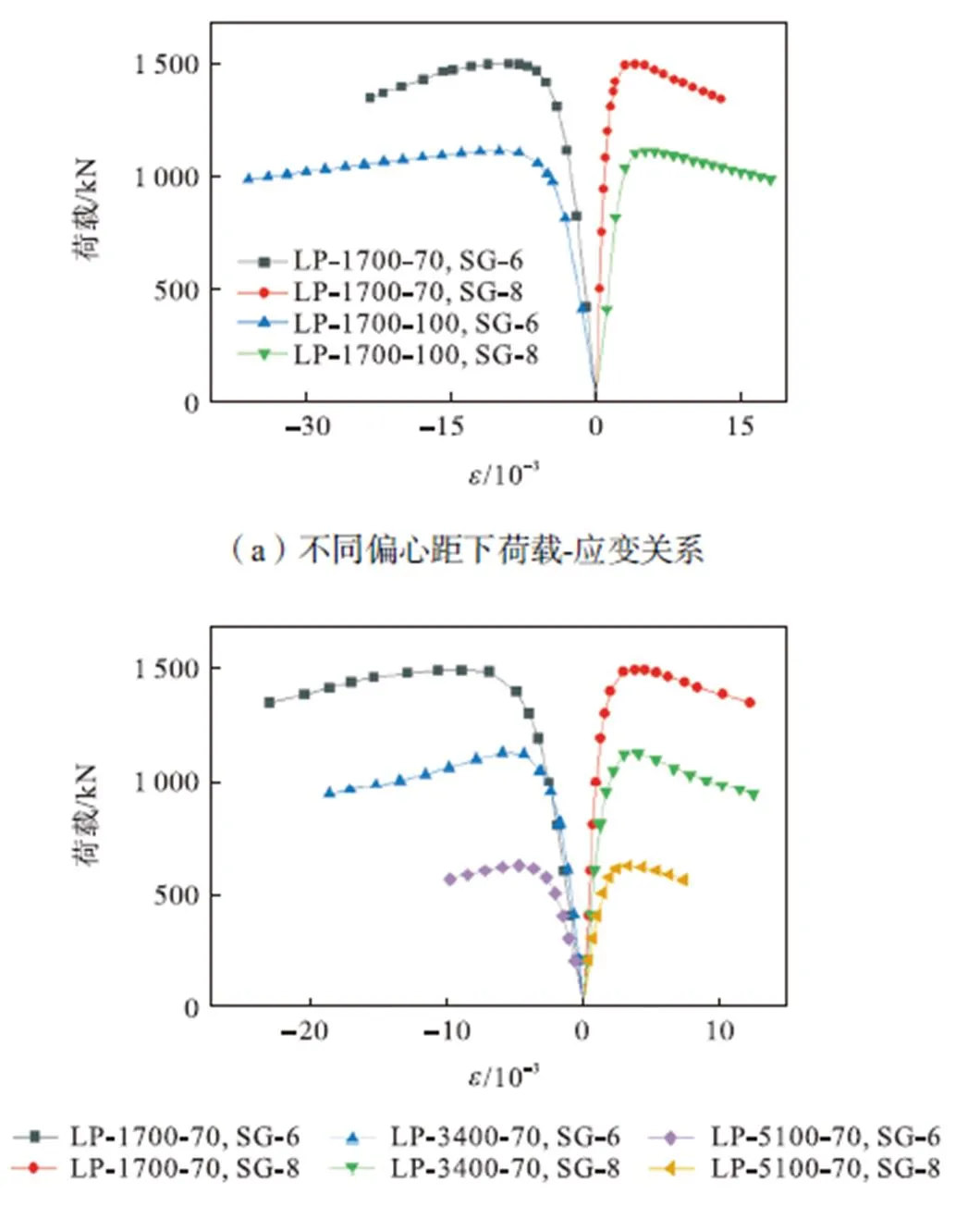
图11 不同长细比和偏心距试件荷载-应变关系曲线

2.4 承载力计算

目前双金属复合管结构的承载力计算方法为只考虑基管承载力，而衬管则只考虑对耐蚀方面的作 用[15,17]．这种设计方法不可避免地低估了双金属复合管的承载力，造成材料上的浪费．因此本文参考碳纤维加固构件的承载力计算方法，利用换算截面法[18]计算复合管在压弯作用下的极限承载力，将衬管视为对基管的加固，将复合管内部衬管实际截面i和i等效换算为基管构件，换算后的截面属于a类截面，计算修正后的复合构件长细比，再按照《钢结构设计标准》(GB50017—2017)[16]中的压弯构件稳定计算公式验算偏心受压构件的稳定承载力，并将计算结果与试验值和基管承载力对比．设衬管材料弹性模量与基管材料弹性模量之比为E，即

式中：i为衬管材料的弹性模量；o为基管材料的弹性模量．

利用换算截面法，将衬管截面面积i、截面惯性矩i根据弹性模量之比换算为基管截面，得到复合构件的换算截面积、截面惯性矩．

由此求出修正后的构件长细比为

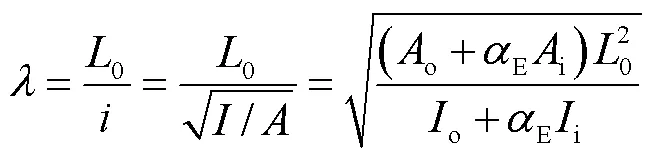
式中：为复合构件长细比；0为受压构件有效计算长度；为复合构件截面的回转半径；o为基管截面面积；o为基管截面惯性矩．

采用式(3)计算复合管构件在压弯作用下的极限承载力．

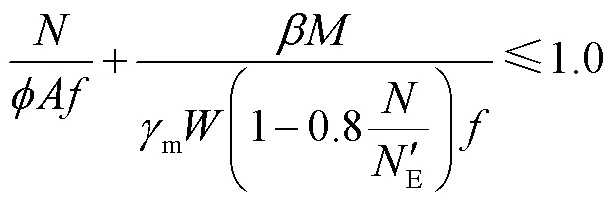
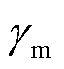
表4为计算结果对比，结果表明换算截面法计算结果c和基管承载力计算结果o均小于试验值，换算截面法的平均误差为7.53%，能较好地估计双金属复合管的压弯承载性能．而仅考虑基管承载力的计算方法平均误差超过20%，采用该方法将严重低估试件承载能力，造成材料浪费．

表4 计算结果与试验值比较

Tab.4 Comparison of the experimental and calculated results

3 结 论

本文以荷载偏心距和试件长细比为参数对7根双金属复合管构件进行压弯试验研究，观察试件在压弯作用下的破坏现象，得到试件的荷载-位移曲线和荷载-应变曲线，并用截面换算法对复合管在压弯作用下的极限承载力进行计算，得到以下结论.

(1) 复合管试件在压弯荷载下的破坏模式均为整体失稳破坏，且展现出良好的塑性变形能力．试件承载力与偏心距成正比，与长细比成反比．

(2) 采用换算截面法计算的极限承载力与试验值误差最大为10.6%，平均误差为7.53%，换算截面法与试验结果误差较小，可以得到较为准确的结果．

(3) 相对于只考虑基管承载力，截面换算法得到的承载力高出15%以上，但两种方法的计算结果仍偏于保守，压弯作用下的复合管极限承载力计算方法有待进一步研究．

［1］闫可安，许天旱，韩礼红，等. 双金属复合管的研究现状与发展趋势[J]. 化工技术与开发，2020，49(10)：45-50.

Yan Ke’an，Xu Tianhan，Han Lihong，et al. Research status and development trend of bimetal composite pipe[J]. Technology & Development of Chemical Indus-try，2020，49(10)：45-50(in Chinese).

［2］朱振兴，杨 璐，王法承，等. 轴压作用下双金属复合管组合作用与承载力分析[J]. 海洋工程，2019，37(4)：98-106.

Zhu Zhenxing，Yang Lu，Wang Facheng，et al. Study on composite action and bearing capacity of the offshore lined pipe under axial compression[J]. Ocean Engineer-ing，2019，37(4)：98-106(in Chinese).

［3］Alcaraz J L，Gil S J，Martinez-Esnaola J M. A fracture condition based on the upper bound method for the extrusion of bimetallic tubes[J]. Journal of Materials Processing Technology，1996，61(3)：265-274.

［4］Wang F C，Li W，Han L H. Interaction behavior be-tween outer pipe and liner within offshore lined pipeline under axial compression[J]. Ocean Engineering，2019，175(3)：103-112.

［5］Focke E S，Gresnigt A M，Hilberink A. Local buckling of tight fit liner pipe[J]. Journal of Pressure Vessel Tech-nology，2011，133(1)：125-133.

［6］Bu Y D，Yang L，Zhu Z X，et al. Flexural buckling behaviour and design of offshore lined pipes under com-pression[J]. Ocean Engineering，2020，214(9)：107-129.

［7］Fathi N. Local buckling behaviour of a corrosion resistant alloy liner in tight fit pipe due to axial compression[J]. Civil Engineering & Geosciences，2009，25(1)：47-69.

［8］Peek R，Hilberink A. Axisymmetric wrinkling of snug-fit lined pipe[J]. International Journal of Solids and Structures，2013，50(7/8)：1067-1077.

［9］Pépin A，Tkaczyk T，Martinez M，et al. Prediction of liner wrinkling during high strain bending of mechanic-ally lined pipe[C]//ASME 2019 38th International Con-erence on Ocean. Glasgow，UK，2019：64-78.

［10］Tkaczyk T，Pepin A，Denniel S. Fatigue and fracture performance of reeled mechanically lined pipes[C]//In-ernational Offshore and Polar Engineering Conference. Rhodes，UK，2012：603-612.

［11］Tkaczyk T，Pepin A，Denniel S. Fatigue and fracture of mechanically lined pipes installed by reeling[C]//Asme International Conference on Ocean. Rio de Janeiro，Brazil，2012：9-18.

［12］Tkaczyk T，Chalmers M，Pepin A. Reel-lay installation approaches for mechanically lined pipes[C]//Off-shore Technology Conference Asia. Kuala Lumpur，Malaysia，2016：304-321.

［13］Tkaczyk T，Pepin A，Denniel S. Integrity of mechanically lined pipes subjected to multi-cycle plastic bending[C]//ASME 2011 30th International Conference on Ocean. Glasgow，UK，2011：187-199.

［14］Focke E S，Gresnigt A M，Meek J，et al. Experimental research on local buckling behaviour of tight fit pipe[C]// Fifteenth International Offshore & Polar Engineering Conference. Seoul，Korea，2005：76-83.

［15］王 纯，毕宗岳，张万鹏，等. 国内外双金属复合管研究现状[J]. 焊管，2015，38(12)：7-12.

Wang Chun，Bi Zongyue，Zhang Wanpeng，et al. Study on composite action and bearing capacity of the offshore lined pipe under axial compression[J]. Welded Pipe，2015，38(12)：7-12(in Chinese).

［16］中华人民共和国住房和城乡建设部. GB 50017—2017 钢结构设计标准[S]. 北京：中国建筑工业出版社，2017.

Ministry of Construction of the People’s Republic of China. GB 50017—2017 Code for Design of Steel Structures[S]. Beijing：China Architecture & Building Press，2017(in Chinese).

［17］Det Norske Veritas. DNV-OS-F101 Submarine Pipeline Systems[S]. Norway：Det Norske Veritas，2010.

［18］周珉璐. CFRP加固轴压方钢管柱稳定承载力试验研究[D]. 合肥：合肥工业大学，2015.

Zhou Minlu. Research on Stability Capacity of Square Hollow Section Columns Strengthened with CFRP Under Axial Load[D]. Hefei：Hefei University of Technol-ogy，2015(in Chinese).

Experimental Investigations of Bearing Performance of Lined Pipe Under Eccentric Compressions

Yang Lu1，Gang Yi1，Wang Facheng2，Zhu Zhenxing1

(1. Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education，Beijing University of Technology，Beijing 100124，China；2. Department of Civil Engineering，Tsinghua University，Beijing 100084，China)

To study the eccentric compression bearing performance of lined pipes，considering the two parameters of member eccentricity and slenderness ratio，seven hydraulically formed X65/316L lined pipe specimens were tested. The test contents include the material property test，3D scanning measurement of initial geometric defects，and bearing capacity test. Comparing the stress process，failure mode，and data results of each specimen，the effects of the specimen slenderness ratio and load eccentricity on the eccentric compression bearing performance of lined pipes were analyzed. The test results show that the failure mode of the specimen under an eccentric load is the overall instability failure，and the specimen exhibits a good plastic deformation capacity after reaching the ultimate load. The larger the slenderness ratio，the more prone the specimen is to instability failure and the shorter the elastic deformation stage of the specimen. Additionally，the stiffness and bearing capacity are significantly reduced. The larger the eccentricity，the lower the specimen’s bearing capacity and its stiffness is slightly reduced. On this basis，a section of the lined pipe is converted by using the conversion section method，and then its ultimate bearing capacity is calculated according to the formula of the compression bending instability bearing capacity of class a section steel pipe in the standard for the design of steel structures(GB50017—2017). The test results of the bearing capacity are compared with the calculated values of the conversion section method. The comparison results show that the bearing capacity of the lined pipe compression and bending members calculated by the conversion section method，considering the contribution of the liner，agree well with the test values，and the average error is below 10% and partial to safety. The design of the lined pipe members by the conversion section method can optimally consider the liner’s bearing capacity. The research results can provide some reference for the design and application of the lined pipe.

lined pipe；eccentric compression；bearing performance；conversion section method；test

10.11784/tdxbz202204033

TU391

A

0493-2137(2023)11-1157-07

2022-04-15；

2022-05-15.

杨 璐（1982—  ），男，博士，教授，lyang@bjut.edu.cn.Email：m_bigm@tju.edu.cn

王法承，wangfacheng@tsinghua.edu.cn.

国家自然科学基金资助项目(51879143)；国家自然科学基金优秀青年科学基金资助项目(51922001)；应急管理部消防救援局重点攻关项目(2020XFZD02).

the National Natural Science Foundation of China(No.51879143)，the National Excellent Youth Science Fund(No.51922 001)，the Science and Technology Project of Fire and Rescue Administration of Ministry of Emergency Management of China(No.2020XFZD02).

(责任编辑：许延芳)