山地低空气流对火炮外弹道产生偏差分析*
王 晋,田军委,*,刘雪松,张 震,雷晓明
(1.西安工业大学兵器科学与技术学院,西安 710021;2.西安工业大学机电工程学院,西安 710021;3.内蒙古北方重工业集团有限公司,内蒙古 包头 014030)
0 引言
在火炮射击中,炮兵作战地域气象条件会对火炮的射击精度产生一定的影响,据研究,在影响射击精度的诸多因素中,气象条件造成的影响占比70%[1],其中,气流是诸多气象条件中对火炮射击精度造成影响最大的因素。在信息化战场环境下,火炮首发命中,先发制人,精确打击是掌握战场控制权的前提[2],但炮兵作战地域具有不确定性,不同地域气流特性也存在较大的差异。在一些常规地形中,火炮可通过试验得到一些实射数据,通过校正准确命中目标,但目前我国火炮试验场地建设并不完善[3],在一些复杂地形对火炮试射的开展较为困难[4]。
在各种复杂地形环境中常存在低空风切变,其中山地地形较为典型[5]。以山地地形为例,当平稳气流途径山地地形时,会受到摩擦、坡度等多种因素的影响而减缓流速,改变流动方向,并且会在背风坡生成涡旋,使其特性产生较大的改变。对于低空飞行的火炮弹丸,不同特性气流对其产生的扰动会对外弹道轨迹产生不同的影响,进而影响火炮的射击精度。目前国内对山地地形特殊气流研究较为成熟,但与火炮外弹道学相融合的研究较少。目前对风场建模的主流方法主要分为根据海拔高度进行分层的平均风模型和风场随机扰动模型[6],这两种方法具有较高的参考价值,但都是从宏观角度去分析风场气流特性,没有针对具体地形地势的风场气流特性进行分析。陈健伟等将单座山地低空气流模型与火箭弹弹道模型相融合并取得了一定的成果[7],但在实战环境中,单座山体出现在战场环境中的情况极少,而单座山体与多座山体的气流特性并不相同,且火炮发射位置地形与弹着点位置地形存在差异,气流特性也不同,对火炮外弹道的影响也存在差异。
因此,基于位势流动理论,将山地气流风场模型与火炮质心运动模型相结合,计算不同情况下多重山峰地形气流对火炮外弹道参数产生偏差的大小并分析原因及规律,为火炮在多座山体环境中射击计算偏差提供理论基础,为后期提高火炮在山地地形射击精度提供参考。
1 山地低空气流模型
在近地面时,低空平稳气流会复杂地形以及该地形表面粗糙度的影响,速度受到一定的影响。对于山体,通常以绕固定圆柱体的不同流线模拟山地外形。现实情况中,山体呈连绵起伏分布,地形复杂且气流特性也会受到较为严重的影响,如图1 所示为位流坐标与山地坐标系,h1、h2为山高。根据圆柱绕流理论,可得出如下多峰流函数表达式[8]:
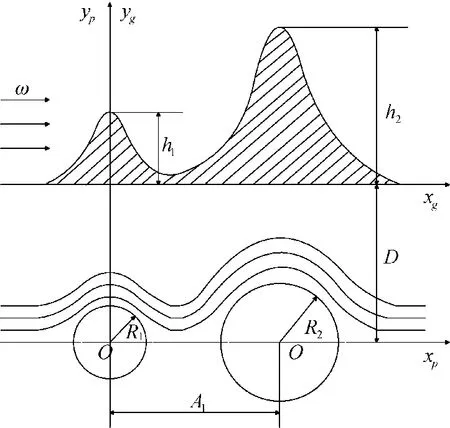
图1 双峰位流坐标与山地坐标系Fig.1 Bimodal potential flow coordinate and mountain coordinate system
式中,A1,A2,…,An-1为各座山体与山体坐标系中第一座山体的距离,R1,R2,…,Rn为不同圆柱半径,ω为初始气流。以双峰体系为例,在该体系流场中任一点速度分量表达式为:
式中,vp为水平速度分量,up为垂直速度分量。
式中,0为地面剪应力,ρ0为空气密度,y0为地面粗糙度。
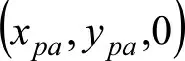
式中,υ 为流动粘性系数,t 为涡寿命,Γ0为黏性涡强度。因此,在山体坐标系中,诱导速度在水平方向分解为vs1、vs2、us1和us2,将圆柱绕流速度与背风涡旋相加并融入摩擦因子,得出双峰地形总气流速度分布:
为方便建立火炮外弹道运动方程,将双重山体坐标系与地面坐标系坐标原点重合,并绕纵轴旋转角度α,通过坐标转换得到气流过山时的三维速度ωa(ua,va,ωa),其分量表达式如下:
为对多重山峰地形气流特性进行研究,特对该地形模型参数进行设置并进行仿真,如表1 所示。
如图2、图3 所示,根据表1 数据基于山地低空气流模型建立y 为1 100 m 水平截面气流分量流线图,x 为11 000 m 垂直截面气流分量流线图,U、W分别为水平方向气流强度分量,V 为垂直方向气流强度。

图2 y 为1 100 m 水平截面气流分量流线图Fig.2 Streamline diagram of horizontal cross-section airflow component when γ is 1 100 m
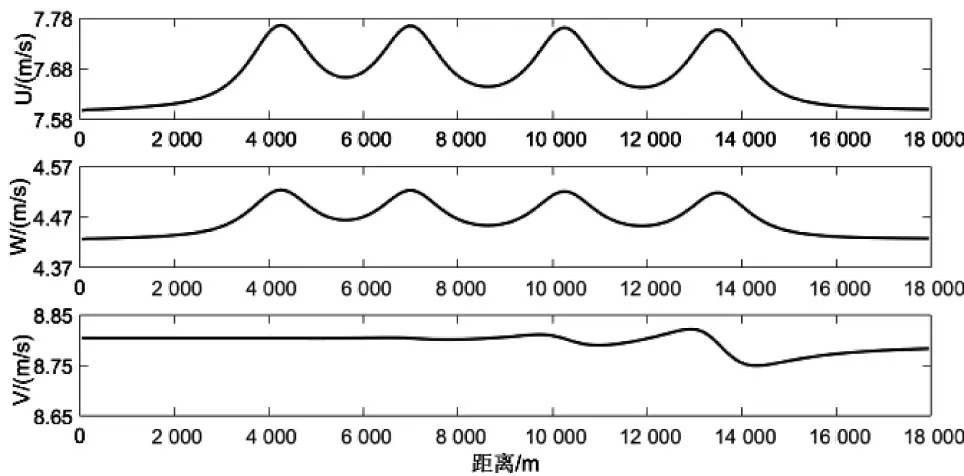
图3 x 为11 000 m 垂直截面气流分量流线图Fig.3 Streamline diagram of vertical cross-section airflow component when x is 11 000 m
由图2 可以看出,水平气流会随着山形的变化而变化,且初始水平气流距离山体距离越远,风速越低;由于选取的测量高度远高于前两座山体,因此,垂直气流变化在后两座山体处较为明显,且距山体顶峰的距离越近,波动幅度越大,但最终趋于平稳。由图3 可以看出,由于流经前一座山体后水平气流分散,对于后一座山体,底层初始水平气流较低,但由于山形流线与水平面夹角呈现逐渐变大,且在山体高度约2/3 处逐渐减小的趋势,水平气流的变化趋势也与此特点相符合,但垂直气流会随着高度的升高而增大。
运用ADS仿真软件进行原理图仿真,可以得到中心频率880MHz,带宽160MHz新型耦合结构带通滤波器与纯感性和纯容性耦合结构S21仿真曲线对比图,如图3所示。从图中可以看出新型耦合结构很好地弥补了容性耦合和感性耦合带外衰减的不足,双边带衰减较均匀,性能有了很大的提高。
为后续气流导入弹道方程,需将地面坐标系气流矢量ωa转化为速度坐标系气流矢量ωc。根据火炮与山体的相对位置,将发射坐标系与地面坐标系进行平移转换,便可根据ωa(ua,va,ωa)获得发射坐标系相对应坐标点的气流矢量ωb(ub,vb,ωb),由于采取原点平移的方法进行转换坐标系,气流的特性并不会受到影响。根据文献[9]引入矩阵A(θa,ψ2),将发射坐标系ωb转换为速度坐标系内气流矢量ωc,转换方式如下:
式中,θa为速度高低角,ψ2为速度方向角。将式(12)代入弹道方程中便可解算出气流扰动对火炮外弹道产生的偏差距离。
2 火炮外弹道模型建立
为研究山地地形低空气流对火炮外弹道产生偏差的影响,根据火炮体外弹道学理论,建立六自由度刚体弹道方程,采用Runge-Kutta 法进行解算。
2.1 计算偏差的六自由度刚体弹道模型
由于本文主要分析低空过山气流对火炮外弹道产生偏差的影响,因此,利用仿真软件建立火炮外弹道6 自由度运动方程,其表达式如下[9]:
上述弹道方程中A 为赤道转动惯量,C 为极转动惯量,θa为速度高低角,ψ2为速度方向角,φ2为弹轴方位角,γ˙为自转角速度矢量,其余相关各变量详见文献[9]。
2.2 四阶Runge-Kutta 法
Runge-Kutta 法是以泰勒级数改进算法,精度高且使用方便,是计算火炮外弹道的一种主要算法[11],其表达式如下:
在利用Runge-Kutta 法计算火炮外弹道时,一般迭代4 次,截断误差阶为O(h5)就可满足精度要求,时间步长ht取0.005 s。
3 仿真及结果分析
以某型155 mm 杀爆弹为研究对象,其技术数据如表2 所示。发射位置气象条件参照我国炮兵地面(即海平面)标准气象条件。
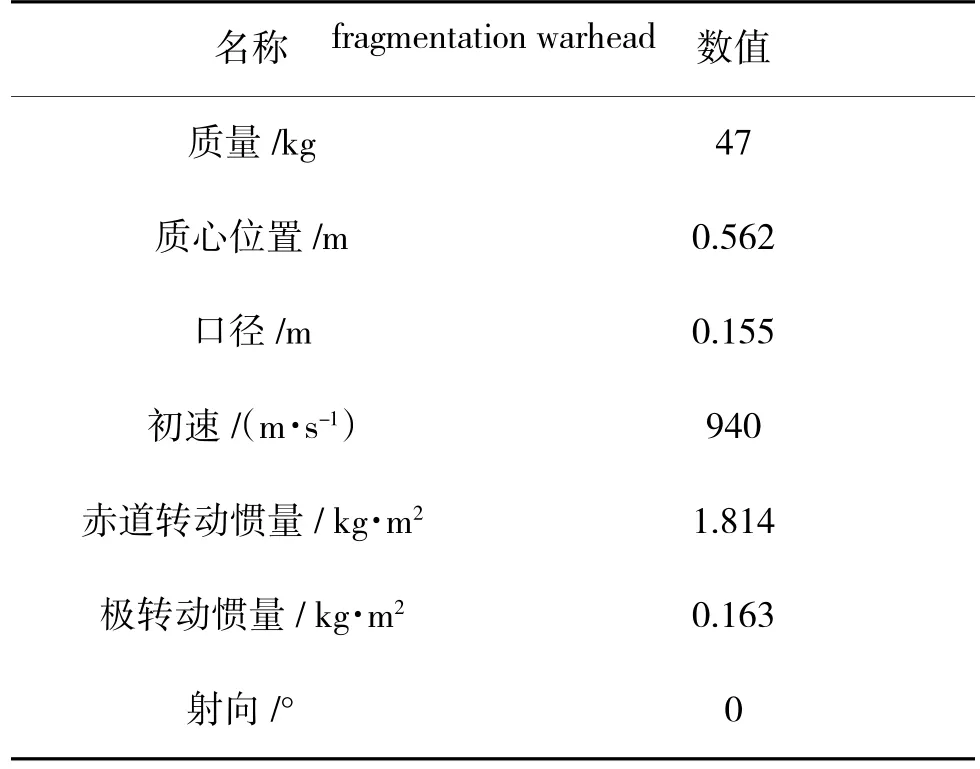
表2 某型155 mm 杀爆弹技术数据Table 2 Technical data for a certain 155 mm blast
将表2 数据与式(12)代入式(13)中,并调用式(14)进行解算。
3.1 不同强度初始气流对火炮产生偏差
由于火炮在中低射角发射的弹丸飞行高度较低,飞行过程中易受到低空过山气流的扰动,导致其产生横向与纵向偏差。因此,根据第1 节表1 地形与气流参数,将火炮发射位置设定在山体1 迎风坡面进行发射,弹着点为山体4 的背风坡面,将山体远前方初始水平气流设定为0 m/s、5 m/s、10 m/s、15 m/s。如下页图4 所示,在不同强度初始水平气流影响下,弹丸的横偏与射程也会出现一定的变化。
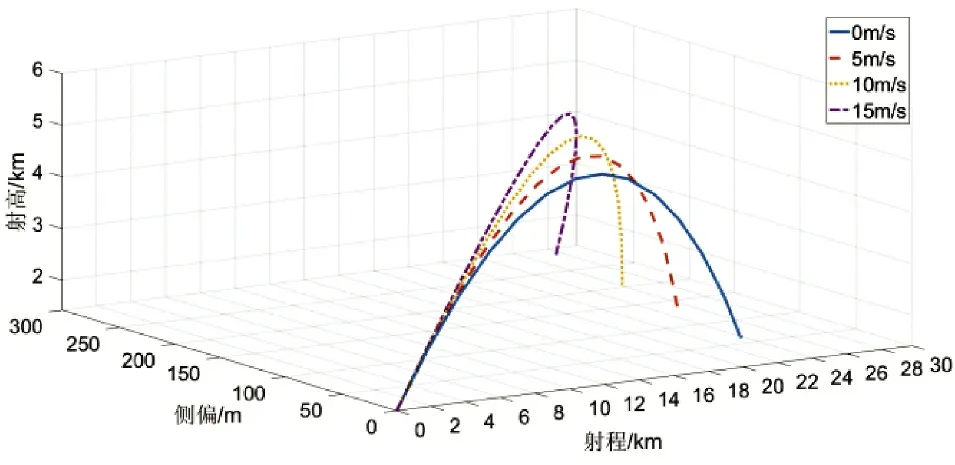
图4 不同强度远前方初始水平气流影响下弹道轨迹Fig.4 Ballistic trajectory under the effect of far ahead initial horizontal air flow with different strength
具体数据如下页表3 所示,通过对比数据可知,不同强度气流对弹丸的飞行高度影响较小,但随着迎风坡气流强度的增大,弹丸受到横向与纵向水平气流强度也随之增大,火炮射程、横偏、射高、偏航角也在不断增大,其中,横偏增加量最为明显,相对于无风时,不同强度气流对弹丸造成横向偏差的倍率分别为237%、342 %、484%,随着气流强度的增大,横偏倍率的增加量也随之增大;在不同水平强度气流影响下,抵达弹着点时弹丸俯仰角变化并不明显。
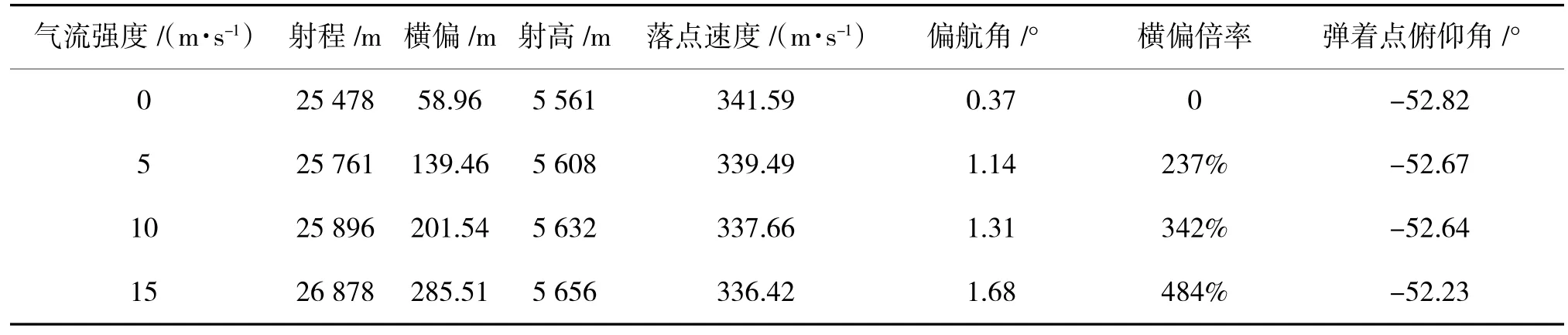
表3 不同强度远前方初始水平气流对弹道影响数据Table 3 Data of the effect of far ahead initial horizontal air flow with different strength on the ballistics
3.2 不同射击地点对火炮产生偏差
由于山体的遮挡,山体迎风面与背风面气流特性不同,对火炮外弹道的影响存在一定的差异,因此,根据第1 节表1 地形与气流参数,将火炮发射位置设定在山体1 迎风坡面进行发射,弹着点设置在山体4 的背风坡面进行迎风坡发射实验;将火炮发射位置设定在山体4 背风坡面进行发射,弹着点设置在山体1 的迎风坡面进行背风坡发射实验;并在相同地形条件下,将火炮设置在平原环境下进行对比实验。图5 为在不同发射位置火炮弹道仿真图。从表4 的仿真结果可知,由于设置射向与气流方向相同,水平气流受地面摩擦影响所产生的横向气流较小。因此,与迎风坡、背风坡发射的弹丸相比,平原时其射程、射高偏大,横偏与偏航角较小,但无风时与迎风坡发射弹丸落点速度相似。由于在背风坡发射的弹丸处于逆风状态,与在迎风坡发射受到顺风状态的弹丸相比,其射程、射高、落点速度等数据都较小,其偏小量分别为1 578 m、92 m、21.41 m/s,相对于迎风坡发射弹丸是射程,背风坡射击距离减少了5.72%。在山体不同位置发射的弹丸其横向偏差量较小,但由于方向不同,在背风坡发射弹丸产生的横偏为负值。因此,在背风坡射击时,可根据实际气流特性调整火炮的射角与装药量。

表4 不同发射位置水平气流对弹道影响数据Table 4 Data of the effect of horizontal air flow in different launching positions on the ballistics
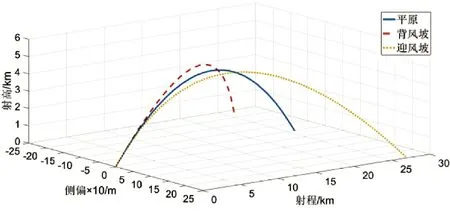
图5 不同发射位置火炮弹道仿真图Fig.5 Simulation diagram of artillery ballistics in different launching positions
3.3 不同射角对火炮产生偏差
在火炮射击时,通常采用调整射角的方式调整火炮的射击距离与射击高度。由于在不同射角下,弹丸飞行高度不同,受到不同高度气流的影响也不同,由于山地地形气流高度较低,因此,在火炮发射过程中要根据弹丸实时飞行高度,计算其在该高度下受气流影响产生的偏差量。本节将火炮发射位置布置在山体的迎风面,具体参数参照3.1 节,设置水平初速气流为10 m/s,如图6 所示,为30 °~45 °4种射角情况下弹道示意图。
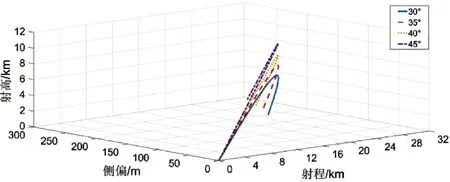
图6 不同射角时弹道仿真图Fig.6 Trajectory simulation at different firing angles
由表5 可知,在30°~45°范围内,射角越大,火炮的射程越远,根据弹道学理论可知火炮最大射程射角近似于45 °;随着火炮射角的增大,火炮射高越高,弹丸受到高层气流的影响越严重,以30 °射角为标准,射角每增加5 °,弹道高分别增加1 351 m、1 608 m、1 688 m,增加量越来越大,但增加量分别占比前一项23.99%,23.03%,19.65%,比值呈减小趋势,进一步表明该火炮最大射程射角在45°附近。由于弹丸受到高层气流的影响严重,附加上山地低空气流的影响,其横向偏差量、落点速度、偏航角也随之增大;由于火炮外弹道具有不对称性,其降弧段与升弧段相比较陡。因此,随着射角增大,升弧段越来越陡,其降弧段也会随之变陡,弹着点处弹丸的俯仰角绝对值也会随着射角的增大而增大,相对于30°射角时,俯仰角增加量分别为-5.32°、-9.59°、-12.11°,增加量分别占比第1 项10.11%,18.22%,23.01%,呈现递增但增加量逐渐减小趋势。
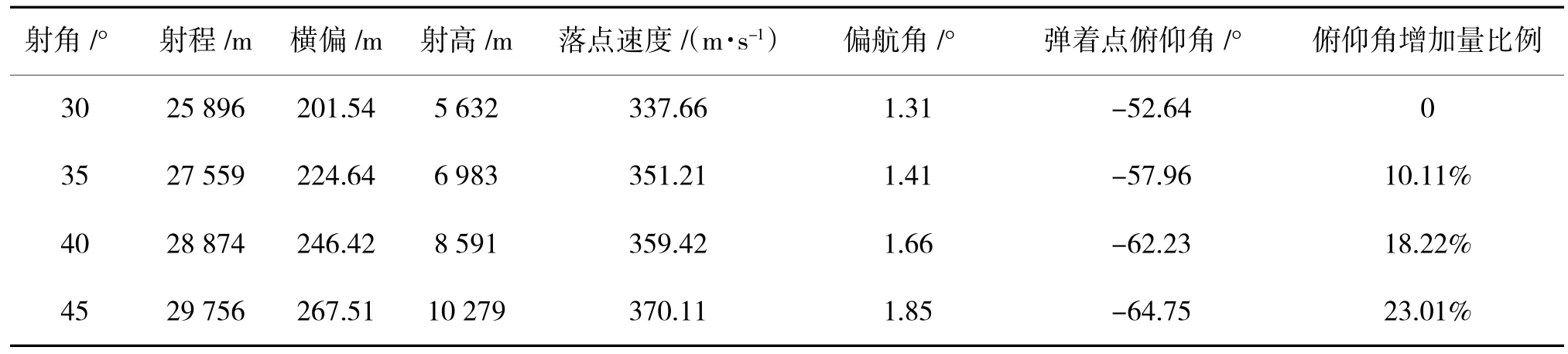
表5 不同射角时山地气流对弹道影响数据Table 5 Data of the effect of mountain air flow with different angle of firing on the ballistics
4 结论
以某型155 mm 杀爆弹为研究对象,基于山地位势流动理论与火炮六自由度外弹道模型分析山地低空气流对155 mm 火炮外弹道产生偏差的影响。根据仿真结果,相对于其他参数,在不同强度初始水平气流对弹丸外弹道产生横偏的影响较大,在实验风速达到15 m/s 时,相对于无风弹道,其偏差量比例约为484%;由于逆风的原因,在背风坡发射弹丸的射程要比在迎风坡发射弹丸距离较近,相对于迎风坡发射弹丸的射程,背风坡射击距离减少了5.73%,且产生的横向侧偏量相差较小,但侧偏方向相反;在不同射角情况下,以30°射角为基准,射角每增加5°,弹道高增加量分别占比前1 项23.99%,23.02%,19.65%,俯仰角增加量分别占比第一项10.11%,18.22%,23.01%,呈现递增但增加量逐渐减小趋势。
由于本文建立的模型较为复杂,在实际环境中,山地低空气流变化速度快,而火炮火控系统无法在短时间内对本文数学模型完成解算,因此,如何简化山地位势流动与六自由度外弹道融合模型,提高实战情况下火炮火控系统的解算速度,还有待进一步深入研究。

