无槽无刷直流电机不同绕组拓扑的分析与比较*

万培熙，赵 博*，鲁炳林，初宇康，杨 鹏

（1.山东理工大学电气与电子工程学院，山东 淄博 255000；2.山东山博电机集团有限公司，山东 淄博 255200）

0 引言

舵机系统作为制导武器姿态控制系统的执行机构，能够根据系统指令对其飞行姿态进行实时调整，从而实现对制导武器的精准操控。如今，为了适应制导武器的发展，舵机系统迫切需要提升性能，电机作为舵机系统的作动器，其性能指标设计也有了新的要求［1-2］。

无刷直流电机（brushless direct current motor，BLDCM）由于其高效率、寿命长、噪声小和较好的紧凑性，被广泛应用到航空航天、军事、机器人等产品中。在传统的无刷直流电机中，由于定子铁心的存在，限制了电机朝小型化发展。同时随着电机尺寸的缩小，绕组的缠绕难度也会越来越大［3］。德国的Dr.F.Faulhaber 在1965 年获得无槽电机斜绕组专利技术，绕组以自支撑的形式粘在定子铁心上，与开槽绕组相比绕线不需要被迫遵循槽的方向，绕组可以在气隙中自由布置，所以无槽绕组又被称为自支撑绕组，这种结构意味着绕组可以有多种形状和拓扑，最常见的是斜绕组和菱形绕组［4］。由于气隙中没有开槽谐波，从根本上消除了齿槽转矩。

近年来很多专家学者对无槽电机性能的提升作出了贡献，DEHEZ B 与MAR-KOVIC M 等合作研究了斜绕组和菱形绕组，指出菱形绕组磁通取决于绕组的形状，通过推导电机两个衰减系数分析磁通量的变化，并使用flex-PCB 技术将斜绕组和菱形绕组功率密度分别提升17.3%和15.3%［5］，但是铜线做挠性PCB绕组很复杂，后DEHEZ B 与BAUDART F 等合作研究了一种“∞”型绕组使电机功率密度再提升10%［6］，MATAGNE E 等人给出了计算二维条件下斜绕组和菱形绕组气隙磁场和电感的解析办法，为优化绕组提供了一种快速计算方法［7］，BURNANDG 等人也对电机绕组有深刻的研究，提出了一种新型的拓扑结构，使电机常数从18%提高到24%［8］。在国内，此类无槽电机本体设计的研究较少，叶金虎对无槽无刷直流电机中的菱形绕组进行了解析［9］，张琴琴等对斜绕组和同心式绕组性能进行了分析，得出了同心式绕组电枢杯优于斜绕组电枢杯的结论［10］。

本文基于菱形和矩形两种不同绕组结构，提出了一种无槽无刷直流电机六角形绕组结构，建立了六角形绕组的理想转矩、反电势和转速数学模型，推导了六角形绕组无槽无刷直流电机的机械特性。在文献［11］中提到了对无槽电机三维仿真模型的展望，最后采用有限元法建立所提绕组结构的三维模型，仿真结果验证了所提六角形绕组模型的准确性，与菱形绕组相比，六角形绕组电机具有更优的机械特性。

1 气隙磁场解析

本文研究的是一种内转子两极三相无槽无刷直流电机，采用双层绕组结构，激励磁场是一个平行充磁安装在铁磁转轴上的圆筒状永磁体作为转子，二维示意图如图1 所示。

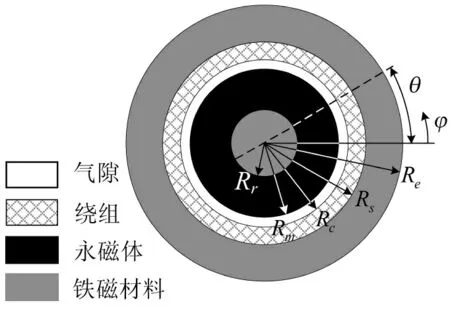
图1 无刷无槽电机二维示意图Fig.1 Schematic diagram of 2-d slotless and brushless motor

图1 中，Rr为转轴半径；Rm为永磁体半径；Rc为电枢绕组内径；Rs为定子轭内径；Re为定子轭外径；θ 表示转子初始角位置。根据文献［12］对永磁磁场的泊松方程进行求解，其在极坐标系（r，φ）处气隙磁通密度的径向分量Br（φ）最终解为

式（1）中，φ 为极坐标系中的角变量；Be表达式为

其中，BR为永磁体剩磁；μr为永磁体的相对回复磁导率，其方程式为

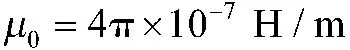
2 六角形绕组结构与主要尺寸设计

2.1 绕组结构

在无槽无刷电机的几种绕组类型中，矩形绕组由于具有两条平行于旋转轴的有效边，在相同的线圈半径和轴向长度时更有利于增加磁链产生更大的反电势。但是由于其端部会随着线圈的绕制逐渐叠加，因此，还要额外扩大定子内部空间，故矩形绕组是不可取的，相比之下菱形绕组的端部不会重叠。

3 种形状线圈如图2 所示，六角形绕组兼顾了矩形绕组和菱形绕组的优势，既做到了尽可能地通过增加磁链来提高电机的反电势，也能处理好绕组的端部问题，简化绕组的制作过程。

图2 3 种形状线圈示意图Fig.2 Schematic diagram of coils of three kinds of forms

它的制作并不是直接绕制成圆筒形状，是将绕组按照一定的形状和尺寸绕制成扁平的元件组，然后相互对接组成一个绕组带，最后将绕组带的首尾拉在一起，最终形成一个双层圆筒绕组，粘在定子轭上共同组成电机的定子。

2.2 六角形绕组反电势微分表达式

由于无槽电机的特点，绕组不需要使用短距来消除谐波，因此，以整距绕组为研究对象，为了方便推导绕组公式，可以将其平展在二维坐标系上进行分析。线圈位置如图3 所示。

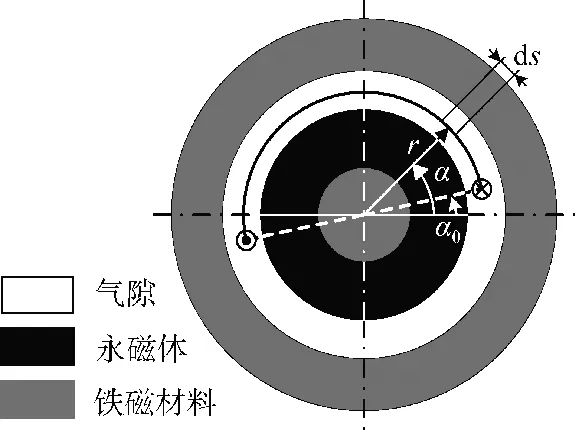
图3 某一时刻一个线圈在磁场中的位置Fig.3 The position of a coil in the magnetic field at a certain time

线圈的任意位置角度为α，α0是线圈的初始位置角，r 为线圈的半径。ds 为线圈的一段微分区域。在二维坐标系中，分析方法是将六角形线圈拆成菱形和矩形分别进行分析，然后再进行组合分析得到六角形绕组表达式。如图4 所示为菱形线圈二维坐标系。

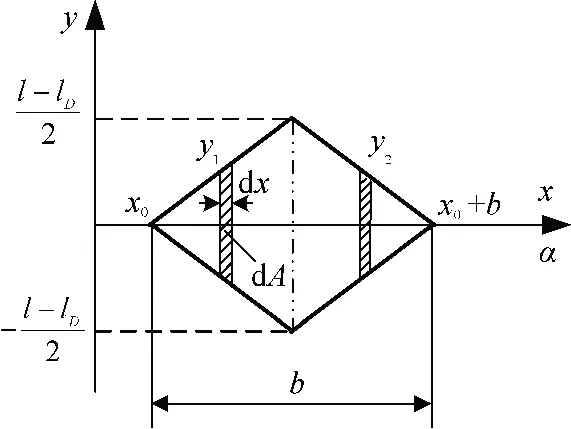
图4 六角形线圈菱形部分二维坐标系展开图Fig.4 2-D coordinate system expanded view of diamond part of hexagonal coil

图中l 为绕组轴向总长度；lD为六角形绕组中矩形部分轴向长度；l-lD为绕组菱形部分的轴向长度。位于圆周位置上的线圈在二维坐标系中的对应关系为

图4 中的菱形左半部分阴影部分y1表达式为

图4 中的菱形右半部分阴影部分y2表达式为

根据磁通量公式得

将式（5）和式（6）代入式（7）可得

式中，Bδ为气隙磁密幅值。由式（8）和式（9）可得一个菱形线圈的磁通量表达式为

同理可求矩形部分磁通量表达式，二维坐标系分析如图5 所示。

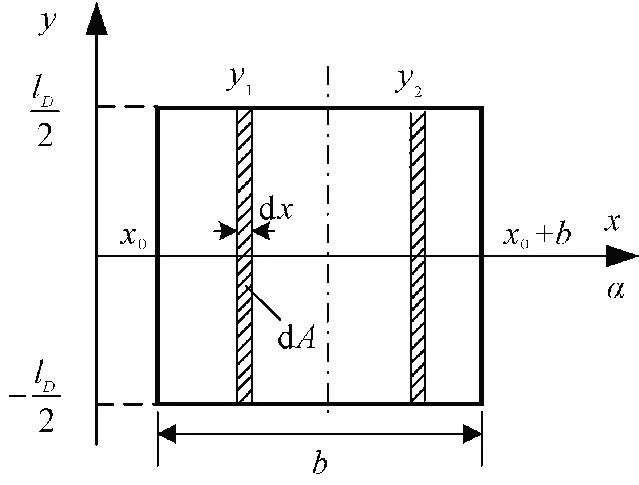
图5 六角形线圈菱形部分二维坐标系展开图Fig.5 2-D coordinate system expanded view of diamond part of hexagonal coil

矩形中阴影部分y 的表达式为

将式（11）代入式（7）可得

由式（12）和式（13）求得一个矩形线圈的磁通量表达式为

结合式（10）和式（14）得到一个六角形线圈的磁通量表达式为

将代入式（15）即可得到一个六角形线圈反电势公式为

式中，ω 为角速度。设绕组密度为γ，则γrdφ0为绕组微分区域的匝数，因此，可得电机反电势的微分关系式为

2.3 电磁转矩表达式

如图6 所示是六角形绕组其中一相的平面展开示意图，三相分别占120°电角度。

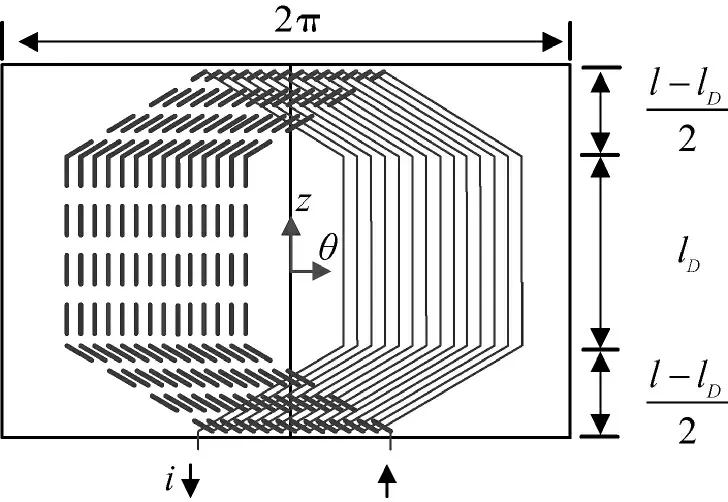
图6 其中一相六角形绕组的平面展开图Fig.6 Plane expanded view of one phase of hexagonal winding

当电机运行在两相导通三相六状态时，绕组电磁力由其电流分布决定。由图6 可见，电流的流向分为两层，虚线处电流流向都为向上，实线处电流流向都为向下。如图7 所示分解其中两相，图中竖线表示电流流向为向上，横线则向下。在横竖线交叉处（Z）电流产生的切向力相互抵消，而A、B 两相中间空白小六角形由S2和S3填充且不重叠，S2和S3重叠部分产生的切向电磁力叠加。

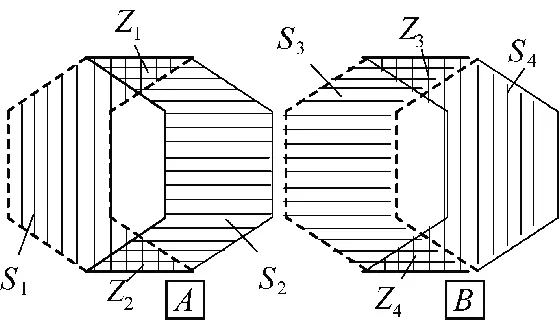
图7 某一导通时刻被分离的A、B 两相绕组Fig.7 Separated a and b winding at a certain conducting time

为便于分析，将中间两个小六角形看成S2、S3与不重叠部分（S1、S4）共同作用的结果。经处理可得4 个单层等效的六角形电流面，如图8 所示。

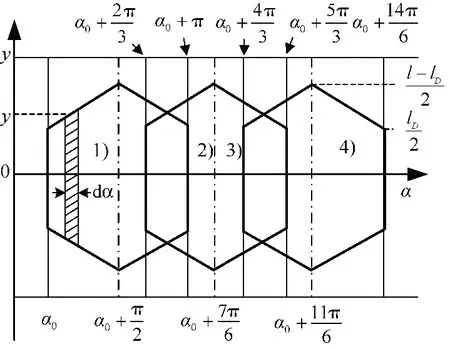
图8 4 个单层等效六角形电流面Fig.8 Equivalent hexagonal current surface of 4 single layers

在分析电机运行的6 个导通状态中，每一个状态都可以等效成如图8 所示的6 层六角形电流面。由电流流向等效的4 个单层六角形电流面产生的切向转矩之和为每一个导通状态的切向电磁转矩，电磁切向力的微分公式为

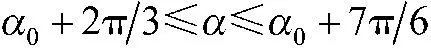
然后4 层切向力叠加，得到电机每个导通状态的切向电磁力为

通过式（24）可见，在通入恒定电流时，电机的电磁转矩可以描述为一个关于起始角α0的正弦函数，表达式为

因此，电机6 个导通状态的电磁转矩波形如图9所示。

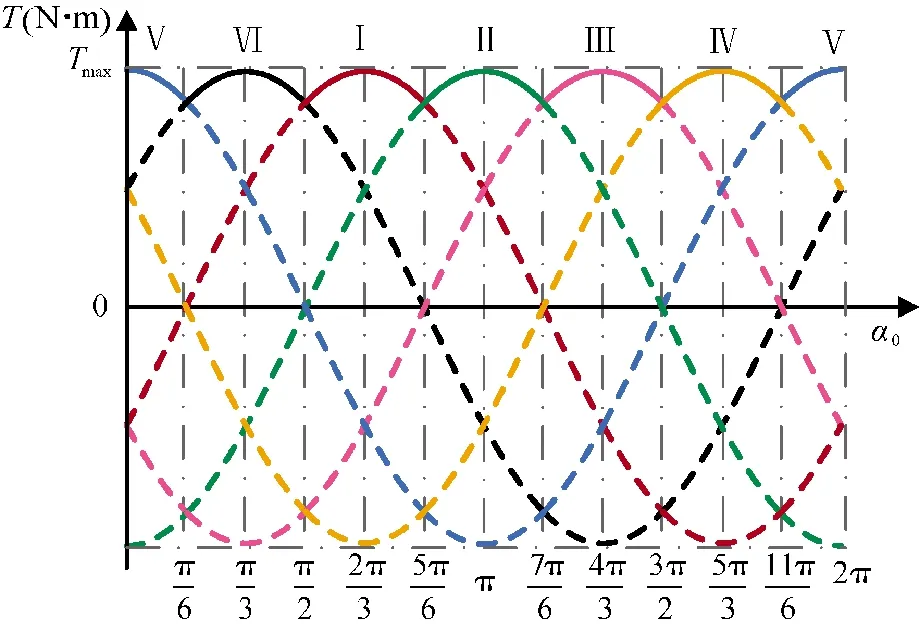
图9 恒定电流下随绕组初始位置角变化的电磁转矩曲线Fig.9 Electromagnetic torque curve of constant current changes with initial position angles of winding

综上，欲求电机的电磁转矩表达式可以用每个导通状态产生的电磁转矩平均值来表示：

通过式（2）得知，在电机产生的电磁转矩已知的情况下，可以通过变换式（26）得到电枢电流的表达式：

2.4 反电势和理想空载转速表达式

由于三相绕组互差120°电角度，因此，求出其中两相的线电压反电势波形，即可得到三相绕组线电压反电势波形。

三相无刷直流电机其中一相绕组的相反电势过零点决定着绕组换相时机，当达到过零点之后，继续导通30°电角度，即是绕组的换相点。无刷直流电机有6 个导通状态，每个状态持续60°电角度，且都是由其中两相线反电势最大值的电角度前后各30°组成，因此，电机每一个导通状态的反电势平均值为

式中，W 为电枢绕组的总匝数。当电机为空载时，由于电枢电流为0，因此，反电势E 等于外加电压源U。

2.5 机械特性分析

式中，rΦ为每相绕组的电阻，单位Ω；ΔU 为外部逆变器开关器件的电压降，理想情况下为0。再将表达式（29）代入最终可得

当给定恒定的电压源时，由式（32）可以得到菱形绕组（lD=0）和六角形绕组转速n 与电磁转矩T 的关系，即电机的机械特性曲线。两种绕组的T-n 曲线示意图如图10 所示。

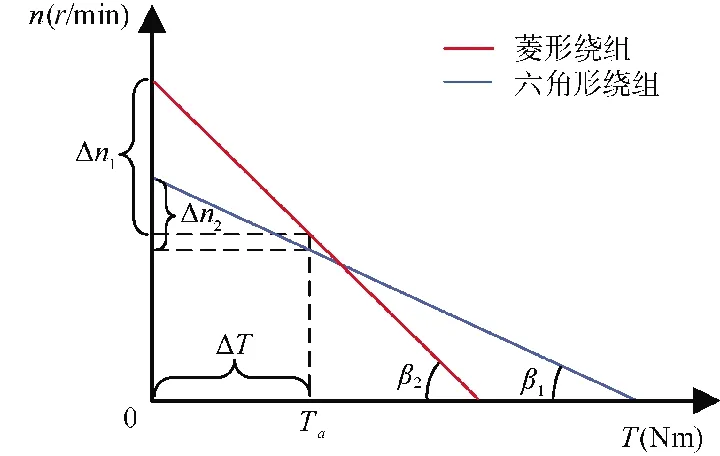
图10 两种绕组的机械特性曲线Fig.10 Mechanical property curve of two kinds of windings

从图10 中可以看出在Ta（拖动相同负载）处时：

3 三维有限元验证

本文以应用于电动舵机中的无槽无刷直流电机为研究对象，样机参数如表1 所示。使用三维有限元仿真进行反电势、转速以及机械特性的验证。

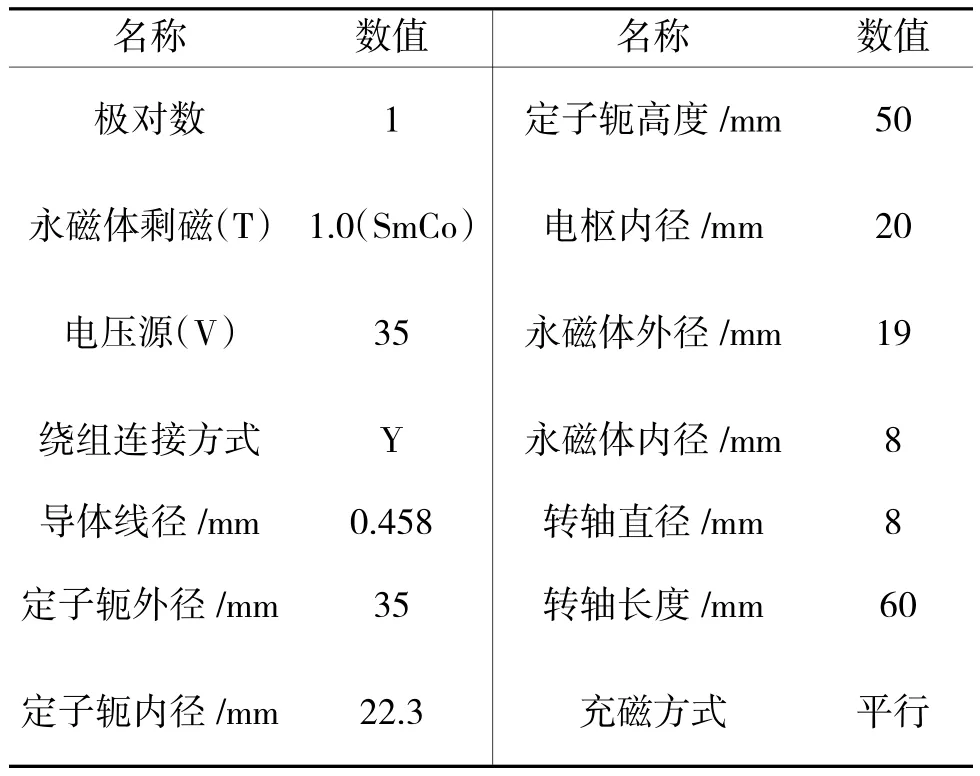
表1 无槽无刷直流电机样机参数Table 1 Prototype parameters of slotless and brushless dc motor

虽然无槽电机具有无槽的特点，但在绕组设计方面可以借鉴有槽电机的设计思路来虚拟定位，总槽数Q 可以按照线圈数来定。本文采用Q=9 即分数槽的设计方式，每相分为3 个线圈，每个线圈占40°电角度，节距可通过式（34）求得

式中，p 为极对数；m 为相数。

通过查表可知样机导线阻值为136 Ω/km，在本文样机中可以求出菱形和六角形单匝绕组周长分别为118 mm 和121.6 mm。故两种绕组单匝的电阻值分别为1.604 8×10-2Ω 和1.653 76×10-2Ω。样机的三维求解模型如图11 所示。

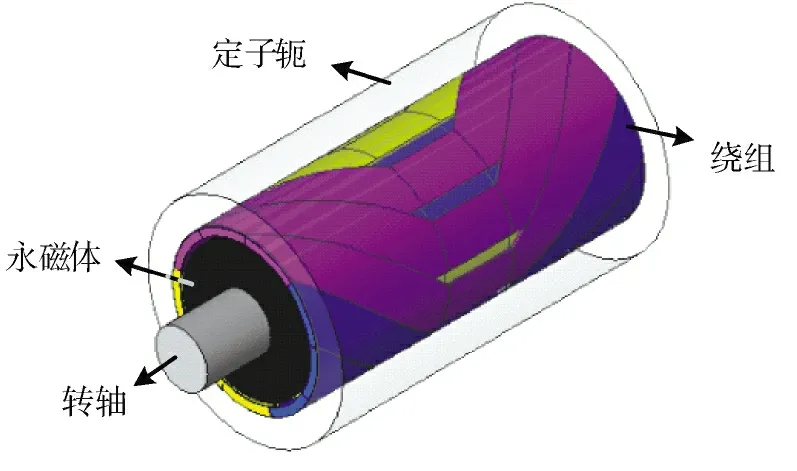
图11 样机三维求解模型Fig.11 3-D solution model of prototype

图12 所示为电机磁密分布云图，在箭头所在线扫过的位置（r=10.5 mm 和h=30 mm）进行径向磁密验证。

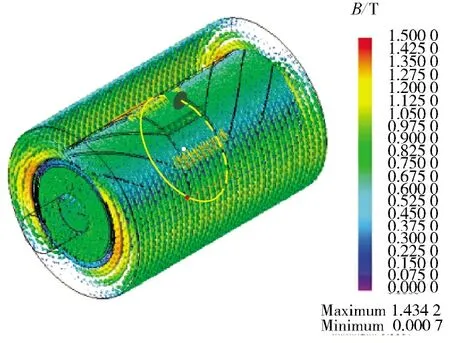
图12 电机磁密分布云图Fig.12 Magnetic density distribution cloud map of motor

使用式（1）可以得到0＜φ＜2π 的气隙磁场径向磁密波形，如下页图13 所示通过与三维有限元仿真结果对比，可见解析与仿真吻合良好。

图13 气隙径向磁密解析与仿真对比Fig.13 Radial magnetic density analysis and simulation comparison of air gaps

图14 为转速在10 800 r/min 时A、B 两相的空载线反电势波形。

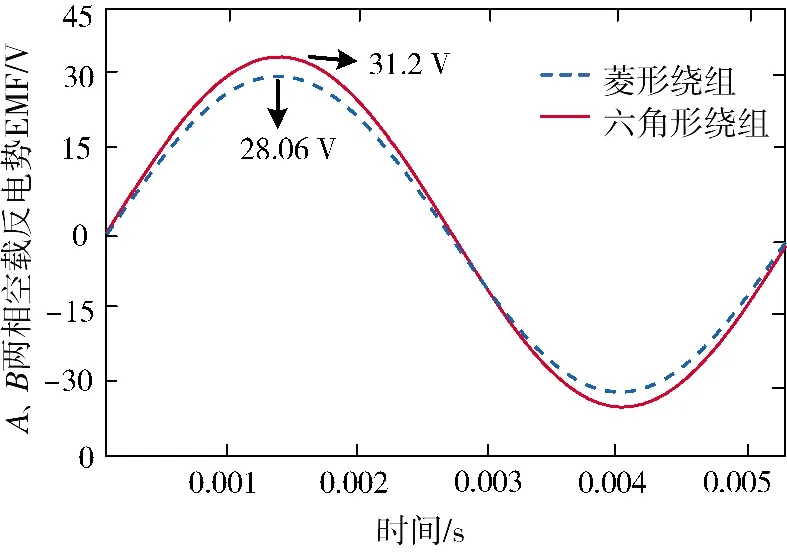
图14 两种绕组A、B 两相的线反电势波形Fig.14 Linear back emf waveform of two phases of two kinds of A and B windings

使用式（28）可以解析出六角形绕组反电势最大值为30.13 V，与仿真结果相比误差为3.5%；使式（28）中lD的等于0 可得菱形绕组反电势最大值为27.4 V，与仿真结果误差为2.4%。

菱形绕组和六角形绕组电机的空载转速以及带有0.16 Nm 负载时的负载转速如图15 所示。

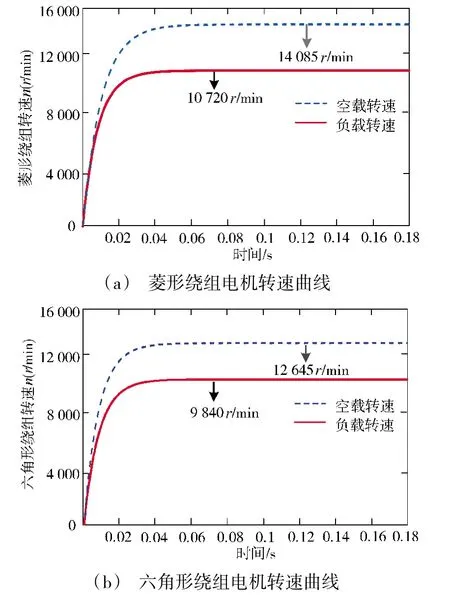
图15 两种绕组样机的空载转速和负载转速曲线Fig.15 No-load rotation speed and load rotation speed curve of two kinds of winding prototypes

由表达式（32）可得菱形绕组电机空载转速以及负载转速分别为14 604 r/min 和11 021 r/min，经与仿真对比误差分别为3.7%和2.8%。而六角形绕组电机计算空载转速以及负载转速分别为13 135 r/min和10 123 r/min，经与仿真对比误差分别为3.8%和2.8%。综上可得图16 所示的电机T-n 曲线。

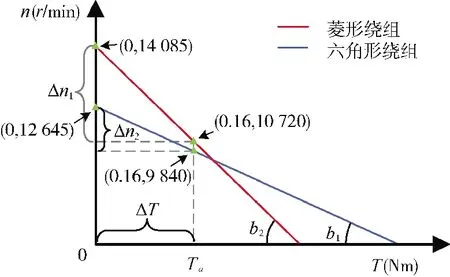
图16 两种绕组的样机机械特性曲线Fig.16 Mechanical property curve of prototypes of two kinds of windings

经过仿真验证，解析公式具有较高的准确性。由关系式（33）和仿真结果对比得知，六角形绕组相比于菱形绕组的确具有更好的机械特性。

4 结论

本文针对导弹电动舵机中高速永磁无槽无刷直流电机的绕组进行研究。分析比较菱形绕组和六角形绕组对电机机械特性的影响，具体结论如下：

1）分析了无槽电机特殊的结构特点，多变的绕组是影响其性能的主要原因之一。

2）基于菱形和矩形两种不同绕组结构，提出一种六角形绕组结构，建立了理想转矩、反电势和转速模型，且当矩形部分为0 时，也适用于菱形绕组的计算。

3）从解析方面对比了两种绕组的机械特性，通过推导出的机械特性公式，得到了两种绕组的负载转速。

4）采用三维有限元法进行仿真验证，仿真结果表明，解析结果与仿真结果吻合良好，新型六角形绕组结构的电机具有更优的机械特性。