电动公交车电池荷电状态的Seq2Seq 预测方法
董红召,王桢,张楠,佘翊妮,林盈盈
(浙江工业大学 智能交通系统联合研究所,浙江 杭州 310014)
电动公交车零污染、低排放、低能耗的特点为环境和能源问题提供重要的解决途径[1].荷电状态(state of charge,SOC)作为电动公交车电池管理系统(battery management system,BMS)中评估剩余可用能量的重要参数[2],可以保障电动汽车的整车能量控制、充放电策略、安全管理等功能稳定运行[3-6].复杂多变的负载和环境导致电池SOC 无法直接测量,因此电池SOC 预测一直是BMS 开发的难点之一.
目前电池SOC 预测方法主要包括模型实验法和数据驱动法.在模型实验法中,来鑫等[7]提出一种基于粒子群优化算法的OCV 曲线优化方法,相比传统HPPC 测试法具有更高的全局精度.罗勇等[8]根据电池组充放电实验,得出不同电池参数的电池容量修正因子,提出带容量修正的安时积分法.寇发荣等[9]利用人工蜂群算法和随机森林优化算法分别实现电池模型参数辨识和SOC估计.孙国强等[10]以磷酸铁锂电池为研究对象,提出一种基于分数阶阻抗模型的锂电池SOC 估计方法.孙金磊等[11]提出基于FFLRS-EKF 联合算法的电池SOC 估计方法,利用FFLRS 修正电池模型,通过EKF 算法修正电池模型估计的SOC.Schwunk 等[12]基于较好参数的综合性电池模型,利用粒子滤波描述电池的外部特性,显著提升SOC 的预测精度.模型实验法在测量实验的基础上建立电池模型,一定程度上能表征电池内、外部特性,但是预测精度依赖于电池模型实验的准确性.模型实验法偏重于电池内部机理及物理特征[13-14],现有研究未考虑电动公交车在实际行驶过程中的电池状态、车辆行驶状态、行驶工况因素.
数据驱动法仅依靠系统输入与输出间的映射关系即可建立SOC 预测模型,无需针对不同电池工作环境来建立不同参数的电池模型.赵轩等[15]提出基于广义生长剪枝径向基函数神经网络的多参数纯电动客车蓄电池的SOC 预测模型.鲍伟等[16]基于电动公交车稀疏采样数据,采用支持向量机算法与贝叶斯优化方法来建立电池SOC 预测方法.电池荷电状态包含时间特征,可将其视为特殊的时间序列[17].在深度神经网络架构中,循环神经网络被广泛应用于时间序列预测[18-19],在时间序列预测上较为突出.Chemali 等[20]在未使用任何电池模型、滤波器等推理系统的情况下,利用LSTM-RNN 预测电池SOC.现有电池SOC 时间序列预测算法难以处理高维数据,且在长序列预测需求下,模型预测精度有待提升.
结合电池状态、车辆行驶状态、行驶工况对SOC 的影响,本研究提出一种电动公交车电池荷电状态的序列到序列(sequence to sequence,Seq2Seq)预测模型.在深度学习框架下,构建WN-Seq2Seq模型分析高维输入特征与预测SOC 序列的关系,为电动公交车能耗控制策略、安全管理提供合理且可靠的参数决策支持.
1 数据来源与特征分析
1.1 数据采集及内容
在实际运行过程中,电动公交车的车载终端将车辆实时行驶数据通过无线通讯上传至远程监控平台.数据内容包括采样时间、经纬度、车速、SOC、 电池组的总电流、总电压、平均温度等,如表1 所示.SOC 为电动公交车电池剩余容量与总容量之比[21],即电池剩余可用容量,计算式为
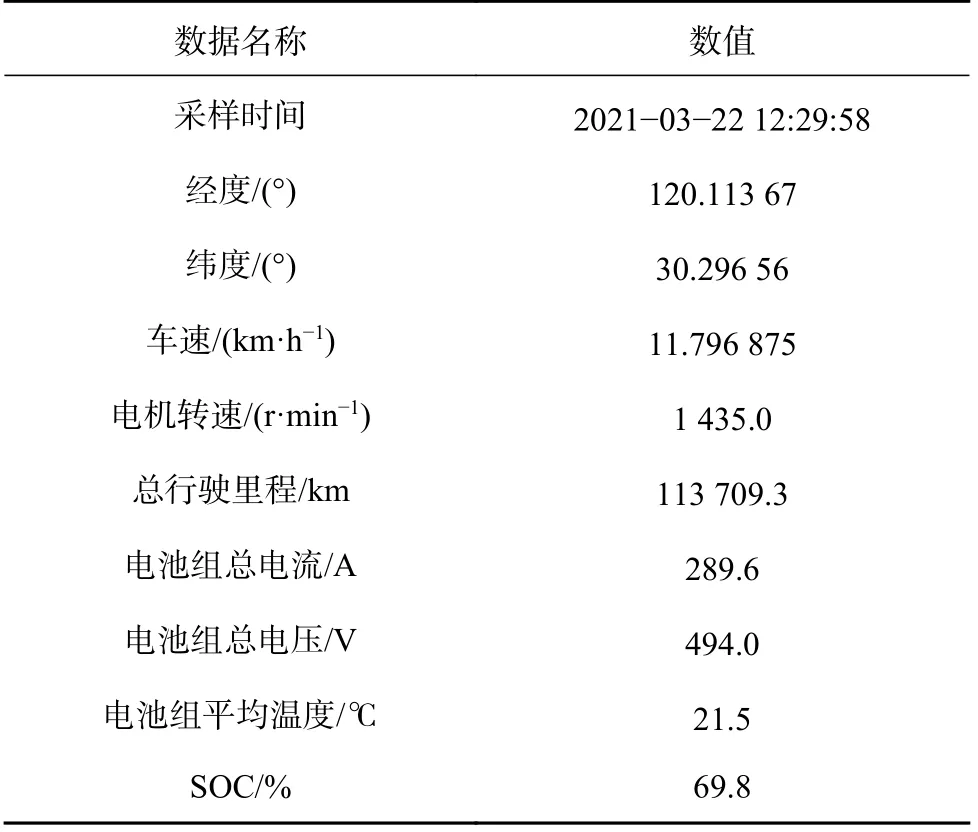
表1 电动公交车的实际行驶数据样例Tab.1 Actual driving data sample of electric bus
式中:Qre为电池中剩余的电池电荷容量,Qdis为最后一次充满电后电池中已经放掉的电荷量.
1.2 特征分析
单一的影响因素无法充分反应电池在实际运行中的特性,因此传统电池SOC 预测方法将电池状态(电压、电流、电池温度特征)作为输入.电动公交车作为完整的电力系统,在实际行驶过程中电池也受车辆行驶状态、行驶工况等因素影响.本研究基于电动公交车的实际行驶数据,在电池状态基础上引入车辆行驶状态和行驶工况,建立多维度、多场景的电池数据库,提升电动公交车电池SOC 预测模型在实际运行场景的准确性及鲁棒性.
电池状态包括SOC、电池组总电流、电池组总电压、电池组平均温度.电池组的电流、电压与SOC 明显相关;电池温度也会影响电池组内部的化学反应;同时SOC 在时间序列上呈高度自相关性.在预测t+1 时刻的SOC 值时,可将t时刻及以前的历史电池SOC 数据作为输入.车辆行驶状态包括车速、电机转速、总行驶里程、经纬度.电池能量消耗受公交驾驶员驾驶风格的差异和道路通行状况而有所不同,车速和电机转速一定程度上可体现二者的变化规律;电动公交车电池会随着时间发生老化;总行驶里程和电池健康状态呈负相关;经纬度可以反应实际道路环境状况,如坡度、海拔等,因此将车辆行驶状态作为电池SOC 影响因素.行驶工况分为平均加速度、平均减速度、平均速度、行驶里程、行驶时间.各行驶工况特征由t与t-1 时刻的公交车实际行驶数据计算可得.电动汽车在不同工况下电池消耗规律有所不同,电动公交车相比普通车辆在行驶过程中还受公交站台等因素的影响,行驶工况更加复杂,因此将行驶工况纳入电池SOC 的影响因素.
电动公交车影响因素及特征如表2 所示.为了验证所取的影响因素对电池SOC 的重要程度及关联程度需要对特征进行筛选,剔除多余或无关特征,提高模型泛化能力.顶层特征选择算法中的稳定性选择筛选特征,其利用二次抽样与选择算法,使得模型有效克服过拟合并加强对数据的理解,选择算法采用随机森林与L1 正则化.在拟合数据后,随机森林会对特征重要程度进行度量.L1 正则化会产生衡量特征重要程度的稀疏权值矩阵.稳定性选择在不同的数据和特征子集上重复操作,自动选取正则化参数以提升模型效果,最终汇总随机森林和L1 正则化的特征选择结果,从而输出特征重要程度(D)[22],结果如图1 所示.
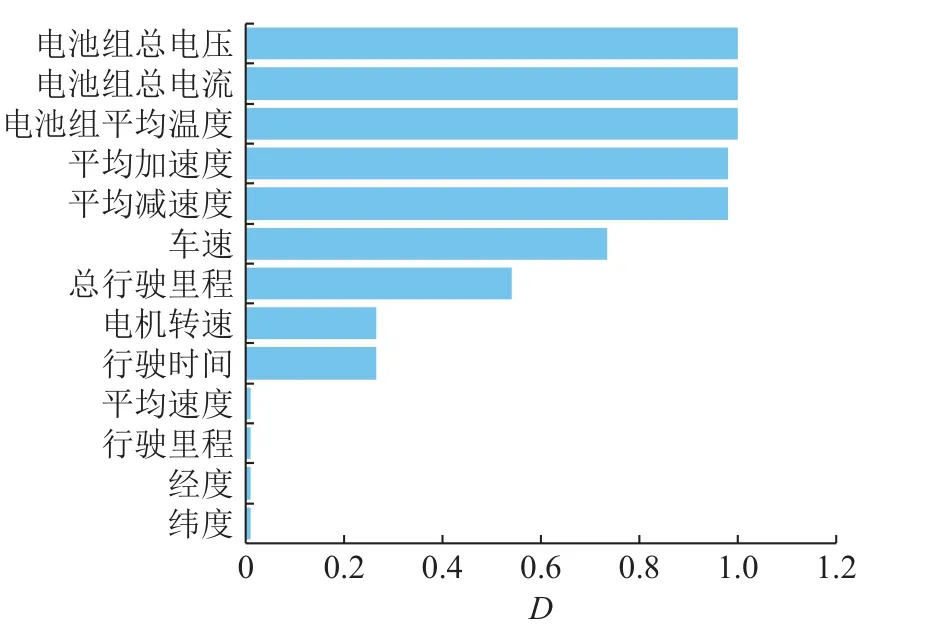
图1 SOC 特征的重要程度Fig.1 Importance degree of SOC features

表2 电动公交车电池的SOC 影响因素特征表Tab.2 Influence factor characteristic of electric bus battery SOC
图1 结果表明车速、平均加速度、平均减速度、总行驶里程和电池组的总电流、总电压、平均温度的重要性较高,特征重要度值都高于0.5.由于SOC 在时间序列上自相关性强.最终所选择的输入特征如表3 所示.
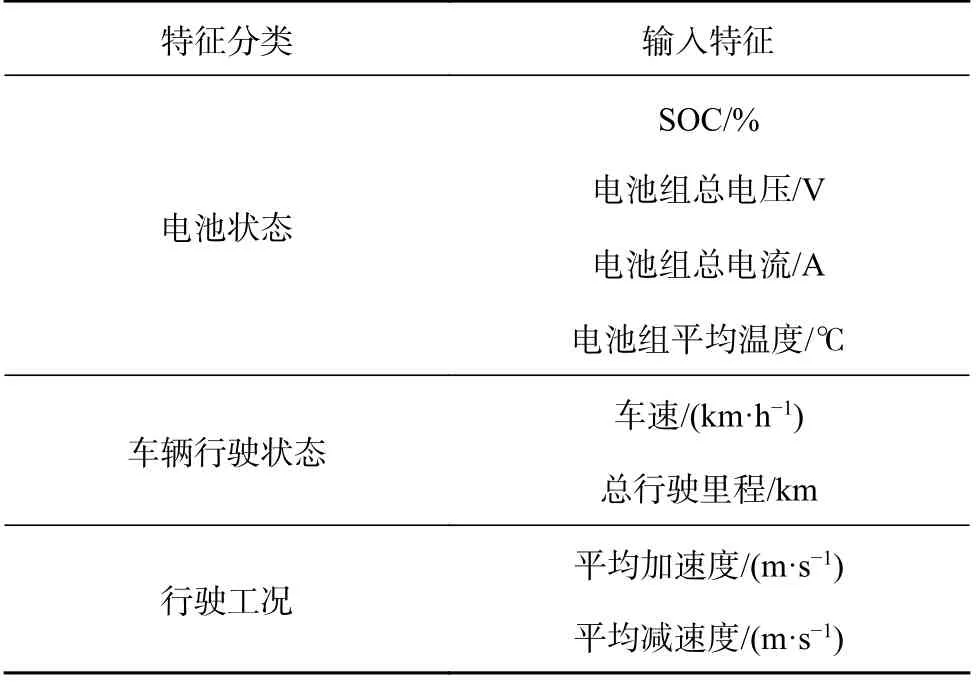
表3 SOC 预测模型的输入特征Tab.3 Input features of SOC prediction models
2 电动公交车电池SOC 预测
2.1 Seq2Seq 模型
Seq2Seq 的编码器-解码器模型将t时刻的输入序列Xt通过编码、解码映射至预测序列Yˆt、学习输入序列与预测序列间的非线性复杂关系中.模型结构体现序列间典型的时间特性,因此该结构被广泛应用在时间序列预测中,如图2 所示,图中ht与d分别为编码器和解码器的隐层状态.电动公交车电池管理系统在提供续驶里程、节能驾驶策略时需要预测长期电池SOC 序列.Seq2Seq模型在面临长期输入序列时会丢失序列中部分信息,模型预测精度随着预测序列长度的增加而下降.
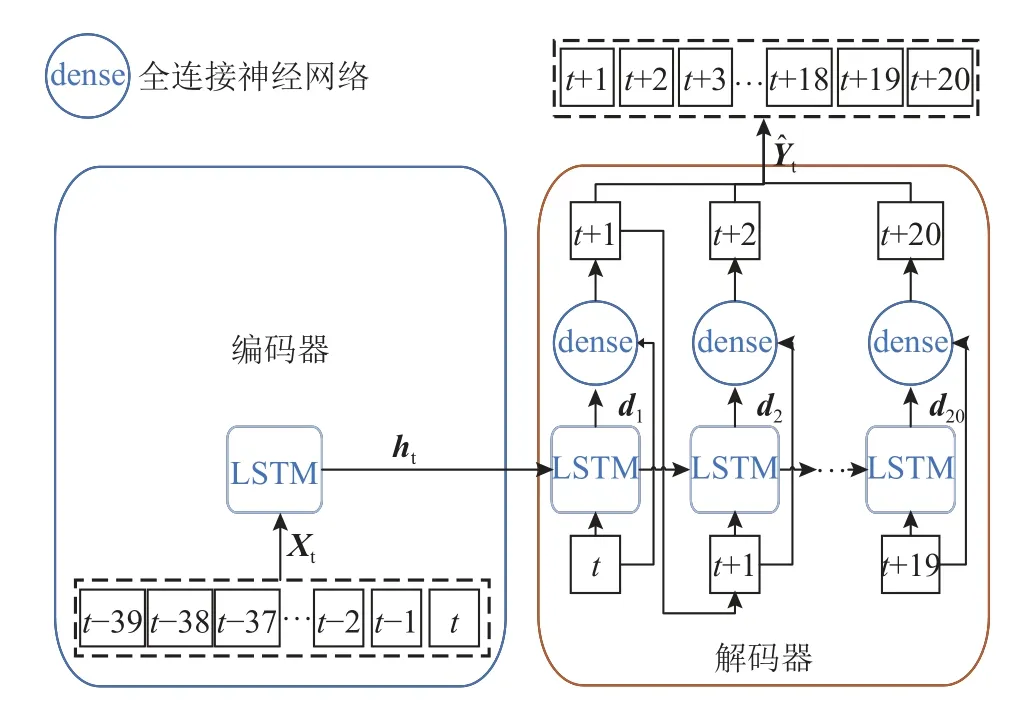
图2 Seq2Seq 的编码器-解码器模型结构Fig.2 Encoder-decoder model structure of Seq2Seq
2.2 WN-Seq2Seq 模型
在Seq2Seq 的编码器-解码器模型结构上融合WaveNet 循环结构,将未来时间段的复杂预测序列拆分为多个简单的局部序列.根据输入序列循环使用单个编码器-解码器结构预测各局部序列,同时在各编码器间传递记忆信息,提高循环预测过程中高维输入序列与局部预测序列的长期记忆信息传递能力,从而提高模型的预测精度.
WN-Seq2Seq 模型在Seq2Seq 的编码器-解码器结构基础上融合WaveNet 循环结构,将长度为M的预测序列按局部预测步长 τ 划分为n个局部预测序列过循环调用单个编码器-解码器预测,最终获得完整的如图3 所示.t时刻编码器将预处理后的第i个 步长为S的 输入序列xt-(S-1)+1,···,xt}通过LSTM 单元进行编码,提取输入序列的内在表征能力,解析电池SOC 影响因素的关键特征信息和时间变化规律,从而产生隐层状态,即

图3 WN-Seq2Seq 的编码器-解码器模型结构Fig.3 Encoder-decoder model structure of WN-Seq2Seq
第i个解码器将作为初始隐层状态,xt作为初始输入,随后解码器采用LSTM 单元将预测值与隐层状态按预测步长t′={0,···,τ-1}产生隐层状态,计算式为
式中:fdec(·) 为解码器非线性映射.
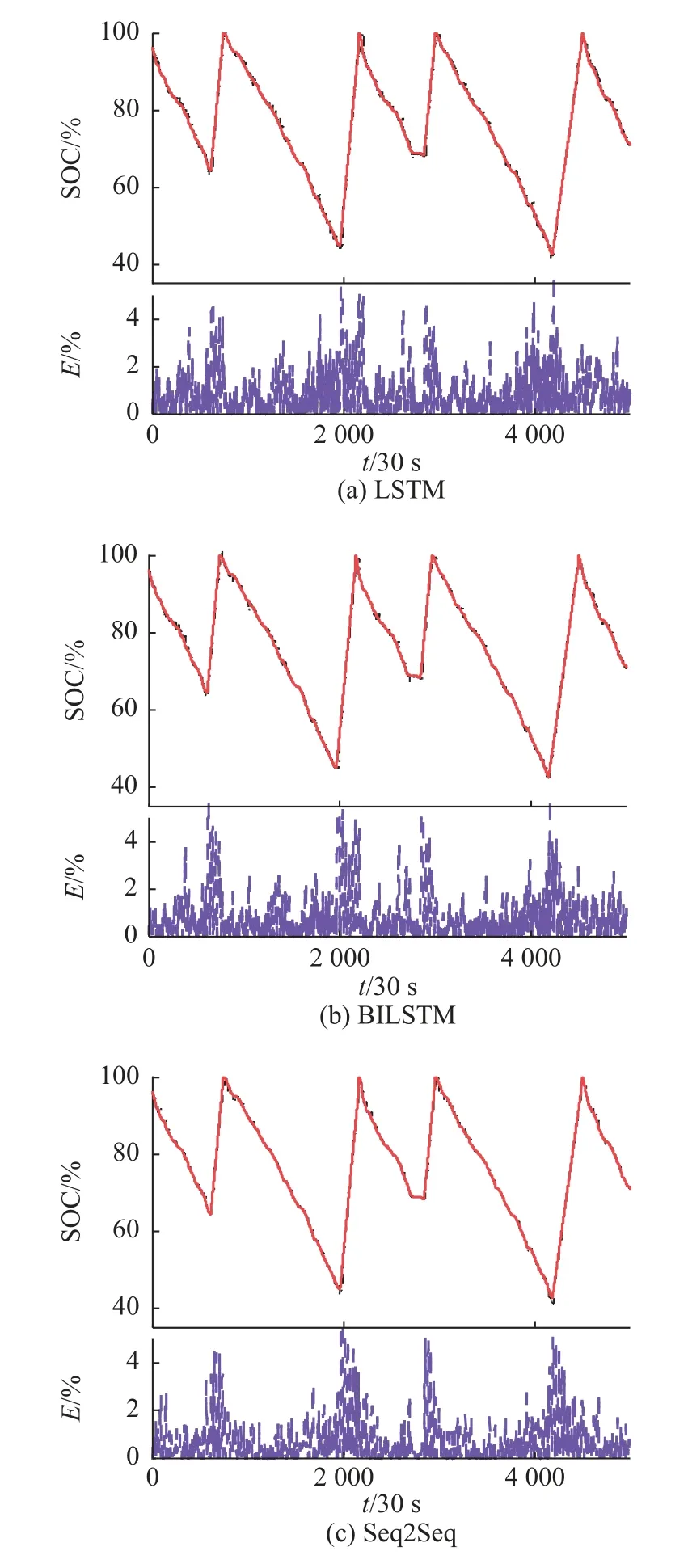
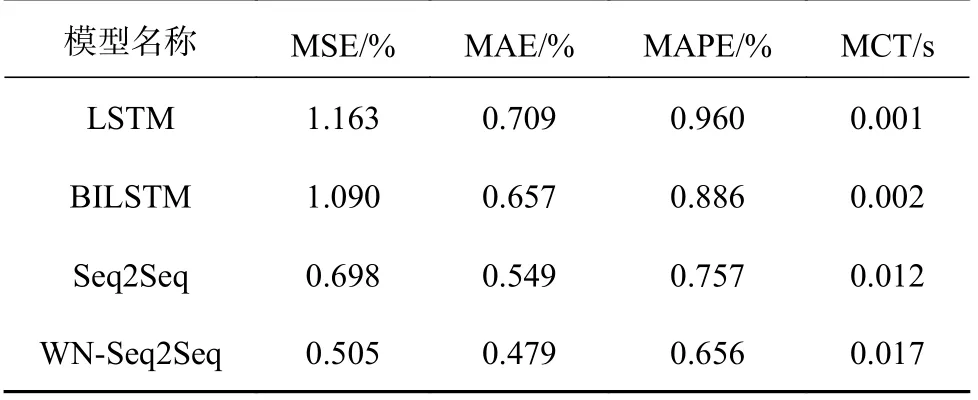
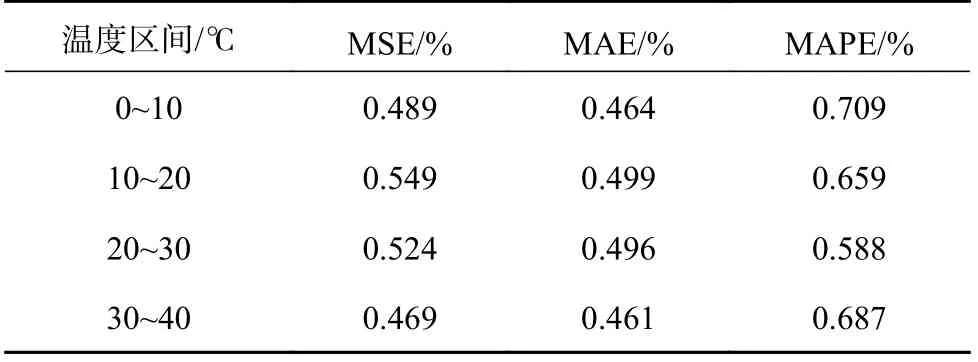
WN-Seq2Seq 模型循环调用单个编码器-解码器最终获得预测序列长度为M的结果YˆM,此时局部预测步长应小于整体预测序列步长 τ 将t时刻作为输入序列,编码器可学习至隐层状态的非线性映.编码器选择LSTM 作为循环神经网络单元如图4 所示. 图4 编码器中LSTM 单元的结构图Fig.4 Diagram of in decoder LSTM unit structure 编码器的更新过程为 图5 解码器中LSTM 单元结构图Fig.5 LSTM unit structure diagram in decoder 解码器的更新过程为 式中:vy、Wy、bW、bv为训练参数. 实验数据来源于杭州市公交公司的比亚迪商用车智能服务系统中4 辆电动公交车实际行驶数据(SOC、电池组电压、电池组电流、电池组平均温度、平均加速度、平均减速度、车速、总行驶里程),各车行驶路线为290 路、193 路、4B 路、188 路.数据采样时间为2021-3-1—2022-2-29,数据采样频率为0.3 Hz,有效数据总量共420 万条.将3 辆电动公交车(290 路、4B 路、188 路)4 个季节不同月份的实际行驶数据作为训练集进行模型训练.一辆公交车(193 路)4 个月的实际行驶数据(1 月、4 月、7 月、10 月)作为模型测试集,验证WNSeq2Seq 模型的预测效果,训练集的数据量为2 656 467 条,测试集的数据量为199 961 条.对原始电动公交车进行实际行驶数据预处理.预处理内容包括异常值处理、缺失值补全和归一化.异常值处理方法为3 σ 准则.缺失值补全采用均值填充与MICE 算法,归一化采用Min-Max. 实验基于PyTorch 深度学习框架搭建WNSeq2Seq 模型,硬件配置为:Ryzen 7 4800H CPU,RTX 2060,16 GB 内存.WN-Seq2Seq 模型训练采用余弦退火和自适应矩估计(adaptive moment estimation,Adam)[23]优化器,训练的学习率从0.001开始,选择均方误差作为训练损失函数,输入序列步长S设置为40,局部预测序列步长为 τ 为5,完整预测序列步长M为20.模型选择均方误差(mean squared error,MSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)作为SOC 预测结果的评价指标. 验证WN-Seq2Seq 模型预测电动公交车电池SOC 的准确性、可靠性及鲁棒性.将该模型与传统时间序列预测模型进行对比,并分析在不同隐层状态维度的预测结果.对比分析隐层状态维度对WN-Seq2Seq 预测结果的影响,实验结果如表4所示.随着LSTM 隐层状态维度增加,预测准确度也在提升,也使模型参数增多,引发过拟合的现象.对比实验结果,当维度从32 增加到64 时,预测精度有所增长,模型预测误差降低16%,但是从64 增加到128 时预测精度略有下降.由此说明简单的增加隐层状态维度无法显著增加WNSeq2Seq 模型的预测精度. 表4 不同隐层状态维度WN-Seq2Seq 预测的评价结果Tab.4 Evaluation of WN-Seq2Seq prediction results for different hidden state dimensions 将LSTM、BILSTM、Seq2Seq 与WN-Seq2Seq进行对比,模型参数设置相同.各模型评价指标及模型计算时间(model calculation time,MCT)如表5 所示,部分电动公交车实际充放电循环下模型的预测效果如图6 所示.从表5 中可得,WNSeq2Seq 的评价指标MSE、MAE、MAPE 分别为0.505%、0.479%、0.656%,MAE 与MAPE 相比于其他模型降低13%~32%,MSE 则降低了27%~65%,无论在预测稳定性和准确性上都优于传统时间序列预测模型. 图6 不同模型预测SOC 曲线与误差的对比Fig.6 Comparison of SOC curves and errors predicted by different models 表5 各模型预测的结果评价值和计算时间Tab.5 Evaluation of prediction results and calculation time of each model WN-Seq2Seq 模型的算计时间为0.017 s,相比其他模型慢了0.005~0.016 s.由于数据采集频率为0.3 Hz,WN-Seq2Seq 模型计算时间满足实际需求.从图6 中可以看出,预测过程中所有模型在充电和放电的切换过程中误差E都有所增大,随后在充电和放电的过程中逐渐稳定.相比传统时间序列预测模型,WN-Seq2Seq 在充放电切换过程时的预测误差变化相对较小.在充放电过程中,传统时间序列预测模型捕捉SOC 值突变的能力和真实值的预估能力较差,预测过程中易出现自偏离现象,而WN-Seq2Seq 模型在预测过程中能够有效对自偏离现象进行调整,从而提高预测真实SOC 值的能力. 分析模型引入不同特征的预测效果,展开消融实验.WN-Seq2Seq 模型加入不同特征后评价指标如表6 所示.在电池状态的基础上分别引入车辆行驶状态或行驶工况,模型预测精度和稳定性都有所提升.加入车辆行驶状态和行驶工况,模型预测效果显著提高,评价指标MSE、MAE、MAPE分别为0.505%、0.479%和0.656%,相比其他特征类别MAE 与MAPE 降低了9%~20%,MSE 降低了20%~21%.电动公交车在实际行驶过程中,车辆行驶状态及行驶工况对电池SOC 有一定程度影响.引入的车辆行驶状态和行驶工况有效地提升模型预测预测准确性及稳定性,引入车辆行驶状态和行驶工况后模型计算时间为0.017 s,与其他特征类别的模型计算时间差距较小. 表6 不同特征类别WN-Seq2Seq 预测的评价结果Tab.6 Evaluation of WN-Seq2Seq prediction results for different feature categories 分析WN-Seq2Seq 模型在单个充放电周期内的预测效果,结果如图7 所示.模型在放电过程预测的效果明显优于充电过程,主要原因是放电阶段车辆行驶状态特征与工况特征提高了模型的预测效果,而在充电阶段车辆处于静止状态,车辆行驶特征与工况特征未发挥作用.同时当SOC 低于50%时,SOC 的下降的速率加快增加了模型预测的难度从而导致模型预测精度有所下降. 图7 单个充放电周期内WN-Seq2Seq 的预测曲线与误差Fig.7 Prediction curve and error of WN-Seq2Seq in single chargedischarge cycle 不同空气温度C下电池实际容量具有差异性,故检验WN-Seq2Seq 在各温度区间的预测效果.取0~10 ℃、10~20 ℃、20~30 ℃、30~40 ℃进行实验验证,各温度区间下模型预测结果的评价指标如表7 所示.部分电动公交车实际充放电循环下模型的预测效果如图8 所示.从实验结果来看,对于评价指标MSE 和MAE,当温度处于30~40 ℃时模型预测效果最优.对于评价指标MAPE,当温度处于20~30℃时,模型预测效果最优.当空气温度降低,电池实际容量会产生变化,从而提高了模型的预测难度.WN-Seq2Seq 模型在各温度区间下都能保证可靠的预测精度及稳定性. 图8 不同温度区间WN-Seq2Seq 预测SOC 曲线的对比Fig.8 Comparison of WN-Seq2Seq predicted SOC curves in different temperature ranges 表7 不同温度区间WN-Seq2Seq 预测的评价结果Tab.7 Evaluation of WN-Seq2Seq prediction results in different temperature ranges (1)为了充分考虑电动公交车电池在实际驾驶场景中的影响因素,在电池状态的基础上引入车辆行驶状态和行驶工况预测电池SOC,实验结果表明加入特征后模型预测精度有所提高. (2)融合Seq2Seq 与WaveNet 循环结构,建立WN-Seq2Seq 模型.实验结果表明,相比传统时间序列预测模型WN-Seq2Seq 模型的预测准确性和稳定性更优. (3)不同温度下电池实际容量具有差异性,分析WN-Seq2Seq 在不同温度区间的预测效果,结果表明模型在各温度区间下都具有优秀的预测效果. (4)所提的电动公交车电池荷电状态WNSeq2Seq 预测方法能将预测的SOC 与BMS 实际上传的SOC 进行相互佐证,对电池管理系统在线诊断意义重大.发现电池能耗规律为电动公交车能量控制策略、安全管理提供科学的参数决策支持.2.3 编码器
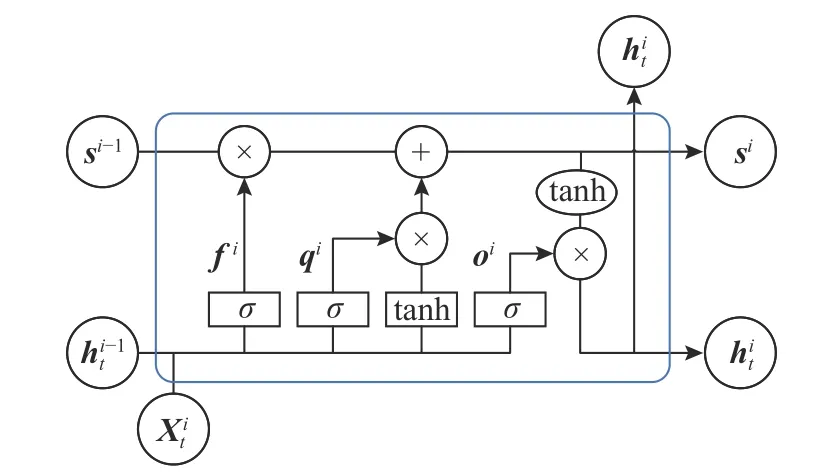
2.4 解码器
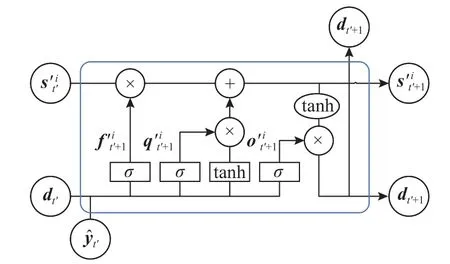
3 实验验证与结果分析
3.1 数据来源与实验设置
3.2 各模型预测结果与分析

3.3 各特征预测结果与分析

3.4 单个充放电周期内预测结果与分析

3.5 各温度区间模型预测结果与分析


4 结 论

