考虑不确定性的维修线性能分析与配置研究
印明昂,刘顺涛,岳龙飞,张子扬
(1.航空工业成都飞机工业(集团)有限责任公司工程技术部,四川 成都 610091;2.东北大学机械工程与自动化学院,辽宁 沈阳 110819)
0 引言
飞机执行任务能力的生成离不开飞机维修线的有力支撑。飞机维修线主要由分解车间与组装车间组成,飞机维修线的性能由车间的维修能力决定。因此,如何利用有限的升级改造预算,对飞机各车间维修能力进行分析,通过各车间维修能力配置优化来提升飞机维修线的性能是一个值得研究的问题。
目前,关于维修能力配置的国内外研究现状如下:步兵等[1]利用着色Petri网分析了通用性维修保障设备的配置对多机种同场次出动架次率的影响;王正元等[2]根据武器装备的毁损情况、故障装备修复能力和作战任务的时限要求,建立了考虑维修能力的战时备件资源配置优化模型;Huang等[3]考虑人力资源的限制,提出了一种具有预定顺序约束的飞机维修人力资源优化配置模型;Feng等[4]分析了面向任务的飞机机队维修人员配置问题,提出了一种基于多智能体的机队维修人员配置方法。
对于飞机维修而言,飞机拆解、维修、存放与组装都需要较大的空间,因此,在维修线建模时除了需要考虑维修车间与组装车间对应的工作,还需要考虑待组装飞机存放对于维修过程的影响。而待组装飞机可以存放在维修车间与组装车间之间的缓冲区内。以上关于维修能力配置的研究大多都是关于维修人员的配置问题,而在存在缓冲区的系统中分析维修线的配置还缺乏相关的文献研究。维修线的配置问题类似于生产线的配置问题,目前关于生产线配置问题的研究如下:刘雪梅等[5]以设备可用度为基础,结合通用发生函数(UGF)法,建立混联生产线的可用度与缓冲区容量关系的数学模型;侯晓博等[6]利用马尔可夫模型研究设备多状态与缓冲区库存的变化规律,以多状态缸盖生产线为研究对象,建立可用度与缓冲区容量的耦合模型;崔鹏浩等[7]以含缓冲区的串联流水线为研究对象,利用深度强化学习算法优化了该生产线的预防性维修策略;Ncnamara等[8]利用仿真模型分析了缓冲区对于不平衡生产系统性能指标的影响;Li等[9]将一个长的串行生产系统分解为多个三机两缓冲系统,并提出了相应的近似求解算法;刘雪梅等[10]考虑装配线时间的随机波动,利用信息熵测量了工位复杂性,并量化分析了操作时间波动对装配线平衡的影响;张惠煜等[11]基于具有缓冲区的排队网络建模方法,提出了一种扩展近似解法以求解系统性能指标。
生产线的配置问题是根据设备的生产能力进行配置,通过协调各个阶段的生产能力,使系统能够稳定地生产产品。然而,对于飞机维修线而言,飞机的维修周期长,并且维修时间存在不确定性。可利用马尔可夫随机过程来构建飞机维修产线模型。目前的马尔可夫过程建模通常以设备状态为基础结合UGF法构建系统模型,但是在存在缓冲区的系统建模中,UGF法仅能给出近似解。本文考虑维修时间的不确定性,且以系统整体状态作为建模基础,构建带有缓冲区的飞机维修线精确求解模型,并以维修数量为基础构建飞机维修线评价标准。
1 问题描述与模型假设
飞机维修线配置如图 1所示。飞机维修线简化为2个串联部分,即分解与维修车间(后简称维修车间)和总装车间,其中第1个部分包含2个独立的维修车间,并且在2个部分之间存在1个缓冲区。无论飞机在任意维修车间维修后均需要通过总装车间进行装配调试。若总装车间空闲,那么该机立即进行装配,否则,该机进入缓冲区等待。本文所指的维修能力配置是维修线中各种维修设备与维修人员综合所体现的维修能力的配置方案。为了方便问题求解,需满足以下假设条件:
a.维修车间不发生饥饿,即始终有飞机等待维修;装配车间不发生阻塞,即飞机装配调试后即可完成维修工作,离开维修线。
b.维修车间的维修任务执行时间、总装车间的装配时间服从指数分布,且参数各不相同。
c.2个维修车间相互独立,且当2个维修车间均拥堵时,总装车间优先服务维修车间1的待组装飞机。
d.缓冲区仅能够容纳1个待组装飞机。
e.各车间的分解、维修、装配和调试设备的故障不影响维修线的维修工作。

图1 飞机维修线配置
2 飞机维修线性能分析
2.1 多状态维修线马尔可夫模型
本文以整个生产线的状态为研究对象,且飞机的维修顺序对于状态转移亦有重大影响,因此,本文的状态既包含各车间的工作状况,即1代表工作,0代表空闲,S代表拥堵,也包含了飞机的维修过程,即(i)代表该架飞机由维修车间i完成分解与维修工作,并且这个代号要一直跟随该机,直到该机在总装车间完成组装调试工作,i=1,2。系统的状态转移如图 2所示,为了方便,每个系统状态均有1个代号,例如①代表状态1,系统的初始状态。λ1和λ2代表维修车间1和维修车间2的维修率,λ3代表装配车间的装配率。
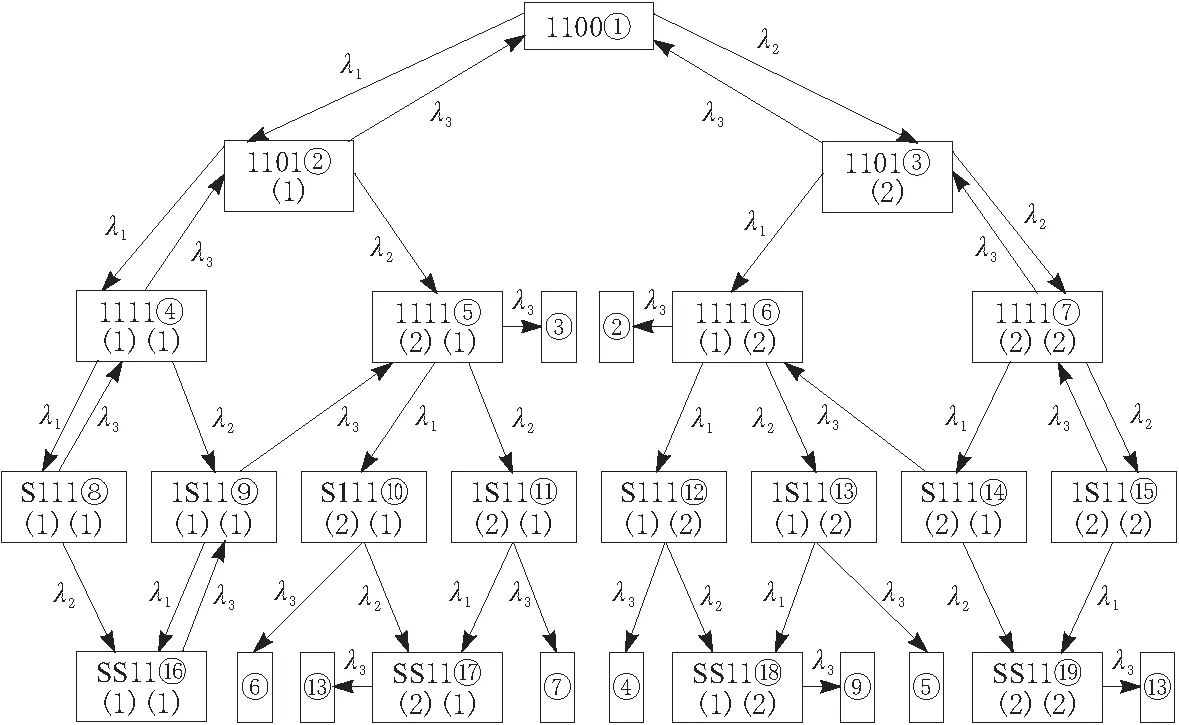
图2 系统状态转移
2.2 维修线性能求解
令P(t)=[P1(t),P2(t),…,Pn(t)]代表t时刻系统的状态分布,n代表系统状态的数量,Pi(t)代表t时刻系统处于状态i的概率,i=1,2,…,n。根据假设b,维修车间的维修任务执行时间、总装车间的装配时间服从指数分布,系统的状态变化由飞机的维修状态决定,根据该模型的状态转移过程,可建立如下方程,即
(1)
A={ai,j}n×n为状态转移率矩阵。根据图 2,ai,j可写为
(2)
假设初始时刻,系统处于全空状态,此时系统初始的运行条件为
P(0)=[1,0,0,…,0]
(3)

(4)

初始时刻各状态均置0,故式(4)的初始状态为
My,z(0)=[0,0,…,0]T
(5)
通过拉普拉斯变换与逆变换,可求解出任意时刻系统状态的分布与各状态之间的转移次数[13]。
3 飞机维修线维修能力配置模型
3.1 缓冲区状态分析
当系统处于状态1、2、3时,缓冲区处于闲置状态,而其他状态下,缓冲区均处于被占用状态,故缓冲区闲置的概率为
(6)
3.2 车间情况分析
维修车间的异常工作状态为堵塞,维修车间的堵塞情况出现在状态8~状态19,其中,状态8、10、12、14表示维修车间1堵塞,状态9、11、13、15表示维修车间2堵塞,状态16~状态19表示2个维修车间均堵塞。
故维修车间1堵塞的概率为
(7)
维修车间2堵塞的概率为
(8)
2个维修车间均拥堵的概率为
(9)
总装车间的异常工作状态为闲置,只有系统停留在状态1时总装车间才会出现闲置情况,其发生概率为
PWE(t)=P1(t)
(10)
3.3 飞机维修数量
系统状态转移由离开状态和进入状态共同决定,单独的离开或进入状态并不能解释状态转移的意义,例如,对进入状态7的状态转移过程,若从状态3进入状态7表示该架飞机在总装车间完成总装调试,可以离场;若从状态15进入状态7表示维修车间2完成飞机分解维修工作,该机进入缓冲区等待。令ri,j代表从状态i转移到状态j的转移过程,维修完成的状态转移集合R为
(11)
飞机维修数量M(t)可表示为
(12)
I(·)为示性函数,当其中表达式为真时取值为1,否则取值为0。
3.4 飞机维修线维修能力优化配置模型
a.优化变量。以不同的维修线配置方案X=[X1,X2,X3]为优化变量,其中,X1和X2分别代表维修车间1和维修车间2的配置方案,X3代表总装车间的配置方案。每个车间的配置方案均对应不同的升级费用与维修率,且Xi的数值越小对应的升级费用越高,维修效率也越高,i=1,2,3。
b.约束条件。以维修线总投入为约束条件,令Ci(Xi)表示车间i在配置方案Xi下所需要的投入,那么约束条件可表示为
(13)
CBudget为维修线的总投入费用。
c.目标函数。以维修线投产后[0,T]时段内的总利润CProfit为最大目标函数,收入CIN为维修飞机所带来的盈利,支出COUT包括缓冲区闲置与车间异常状态引起的损失。因此,有
CProfit=CIN-COUT
(14)
令CM表示每架飞机维修的盈利,故
CIN=CM·M(T)
(15)

(16)
4 案例分析与验证
以某飞机维修线为研究对象,该维修线包含1个维修车间与1个总装车间,并且以维修时间均值代表各车间的维修能力。其中,维修车间的维修能力为40 d/架,总装车间的总装能力为35 d/架。为了扩大产能决定将现有的维修车间与总装车间升级,并新建1个维修车间。在不同维修线配置方案下,各车间的维修/总装能力与相应的升级改造费用如表 1所示。
各状态间的转移率λi(i=1,2,3)为
(17)

满足维修预算限制的维修策略组合所能带来的利润如表 2所示,其中,在X=[3,2,1]时获得最大的CProfit为7.60亿元,此配置方案下飞机维修线共需投入10.50亿元。

表1 各车间升级改造参数
根据表2中维修线配置方案X=[3,2,1],在运行时段内预计维修飞机数量M(T)为8.56架,共获利CIN=17.12亿元。支出COUT=9.52亿元,具体支出明细如图 3所示。在所有支出中,总装车间的空闲所带来的支出最大为3.76亿元,约占总支出的39.5%。
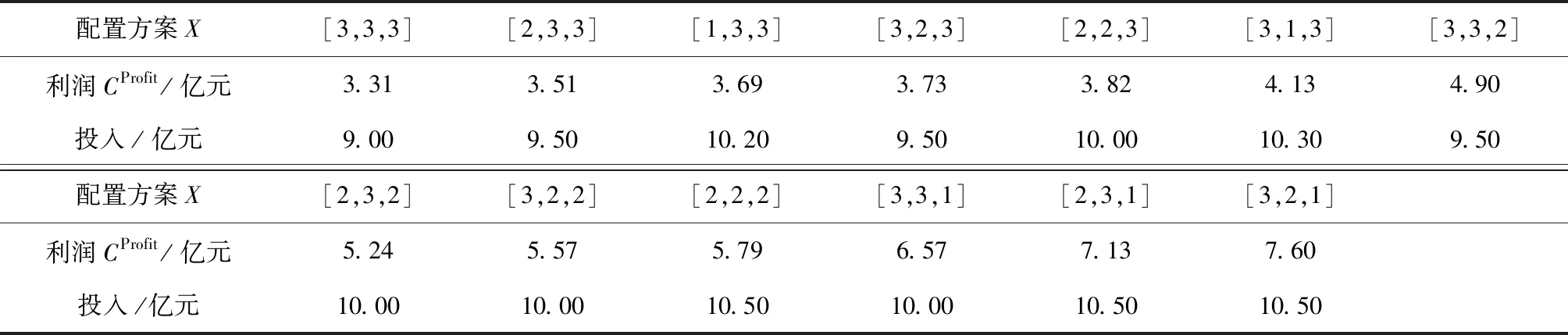
表2 各配置方案的利润与投入

图3 最优配置下各部分支出明细
5 结束语
本文依据某飞机维修线为研究对象,以整条维修线状态为整体进行建模,针对飞机维修时间较长且存在波动性的特点,利用马尔可夫过程以及状态间转移数量,推导一段时间内维修飞机总数量。通过算例验证,本文方法能使飞机维修线在有限的预算下得到获利最大的配置方案,实现了维修线维修性能和成本控制的有效管理。本文系统属于一个小规模的维修模型,若模型规模进一步增大会使模型的状态空间爆炸,可利用深度学习算法求解维修线的维修数量并利用多智能体优化算法寻优。

