问题·想象·实验:圆锥体积的学材设计与教学路径新探
罗永军 沈建琦




【摘 要】做思結合是发展学生想象力的一条重要途径。在圆锥体积的学习中,教师采用“问题—想象—实验”的学习路径,通过“提出问题,开启想象;聚集问题,展开想象;做思结合,验证想象;观察猜想,拓展想象”的教学过程,层层递进,融想象力发展于动手实验操作,形成想象,增强回路,从而推动学生理解不同物体体积之间的关系,提升学生的空间想象水平。
【关键词】圆锥的体积;想象;实验
做思结合是发展学生想象力的一条重要途径。小学数学教学中,每个学习领域的内容都需要学生动手实验操作[1],圆锥体积公式的学习也不例外。那么,如何让学生通过动手操作实验来理解圆锥与圆柱的体积关系,从而提高空间想象水平呢?为此,笔者进行了如下思考与实践。
一、课前思考
圆锥、圆柱都是旋转体,圆锥的体积等于与它等底等高圆柱体积的[13],但学生直觉上会误以为是[12],这主要是受平面图形面积的负迁移影响。在平面图形中,两个形状相同的直角三角形,它们的面积都是等底等高长方形面积的[12],因此,对于直角三角形沿直角边旋转后得到的圆锥,学生也容易“同形继承”,认为圆锥的体积是相应圆柱体积的[12]。
圆锥的体积公式在小学教学中难以通过数学推导得到。[2]教学中,教师一般采用实验法,让学生在圆锥容器中装满水(或沙),倒入等底等高的圆柱中。通过这样的操作活动,学生很快就能得到“圆锥的体积等于与它等底等高圆柱体积的[13]”的结论。整个学习过程中,实验操作很简单,实验结果也很清晰,一切都很顺利。可是到了独立应用阶段,或是过一段时间后,又经常有学生把[13]写成[12],也有的忘了乘[13]。为什么会这样呢?问题就出在“实验”上。如果教师只是按照上面所述教学,那么学生完成的只是教师要求的操作步骤,而为什么要做倒水(或沙)的实验,为什么要选择等底等高的圆锥容器来倒水,倒水时要关注什么,倒完水后圆柱体积剩下的[23]是什么形状……这些问题学生都没有机会思考。因此,看上去学生该做的都做了,课堂气氛也很好,大家都积极参与,实际上学生只是在“奉命操作”,而不知其所以然。
因此,教师在设计实验活动时,要避免把操作等同于实验,而要把实验操作的动因前置,让学生经历“问题—想象—实验”的探究过程,从而促进学生进行数学思考,提高学生的空间想象水平。基于上述分析与思考,笔者确立了如下教学目标。
(1)通过将平面图形旋转成立体图形的操作,使学生直观感知二维图形与三维图形的联系,为学生的想象提供经验基础。
(2)通过圆锥、圆柱等立体模型的制作与变形,使学生直观感知形体大小,为学生进一步探索体积关系提供直接经验,提升学生的想象水平。
(3)通过对圆锥、圆柱体积关系变式的观察与思考,引出各种猜想,进一步提高学生的想象水平。
二、教学实践
(一)提出问题,开启想象
“动脑想”是想象力发展的前提。本课中所用的实验法以动手、动脑为特点,然而动手不一定引起动脑,学生也可能只是按部就班地进行机械操作。因此,教师教学时要把“想”前置,以问题为导向,让学生在观察中思考,在思考中质疑,从而引发学生的认知冲突,使学生在猜测中开启想象。
1.谈话引入
教师提问:“我们最近在学习有关圆柱的知识,大家感触最深的是什么?”
学生七嘴八舌,纷纷发表自己的“感言”。有的说,圆柱和长方体一样都是柱体,可以想象成许多个平面叠起来;有的说,用一个长方形能卷成圆柱让人印象深刻;还有的说,圆柱可以由一个长方形旋转得到让人印象深刻;等等。
2.提出问题
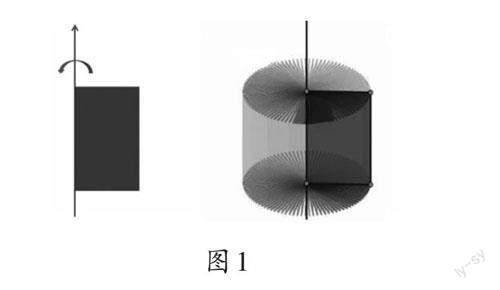
教师顺着学生的回答,用课件动态演示“一个长方形沿着它的长或宽旋转一周就可以得到一个圆柱”(如图1),并引导学生思考:在这个长方形上剪一刀,将它分成形状相同的两个图形,再分别旋转一周,会得到什么立体图形?
学生先独立思考,再小组讨论,最后全班交流。
师:你是怎样平分长方形的,想象一下,旋转后的图形是什么样的?
生:横着从中间剪一刀,分成两个相同的长方形,旋转一周后是两个相同的圆柱。
生:竖着从中间剪一刀,分成两个相同的长方形,旋转一周后,得到一个圆柱和一个像环形那样的柱体。
师:我们可以把它叫作环柱。
生:沿对角线剪开,是两个相同的三角形,旋转一周后是两个圆锥。
生:只有一个圆锥,另一个不是圆锥,是镂空的柱体,镂空的部分是那个圆锥。
生:是圆柱去掉等底等高的圆锥剩余的那个部分。
……
根据学生的反馈,教师利用动态数学软件演示将平面图形分别旋转成立体图形。
设计意图:对于旋转体,计算其体积一般要用到微积分知识,而小学生只能用实验法解决。在教学中,教师回到旋转体的本源,以问题为驱动,让学生想象二维平面图形旋转成三维立体图形的样子,从而产生验证想象的需求,为进一步探索奠定基础。
(二)聚焦问题,展开想象
当研究问题提出后,有的可以马上解决,有的则需要审辨。对于要进一步重点研究的问题,教师可以引导学生进一步明确相关信息,明晰问题的思考点,有效促进学生有针对性地进行思考与想象。
教师提问:把长方形一分为二,得到两个完全相同的平面图形,将它们分别旋转一周后,两个立体图形的体积相等吗?如果两个立体图形的体积不相等,体积比会是多少?
让学生先独立想象与计算,再在小组内讨论交流。
师:我们一起来讨论把长方形上下分、左右分、对角分的三种情况。
生:上下平均分,旋转一周后得到的是两个完全相同的圆柱,它们等底等高,体积是相等的。
生:左右平均分,旋转一周后得到的是两个不同的立体图形,里面那个是圆柱,外面那个是环柱体,体积不相等,它们的底面积之比是1∶3,体积比也是1∶3。
师:旋转前两个长方形的形状、大小是完全相同的,旋转后得到的体积怎么会不相等呢?
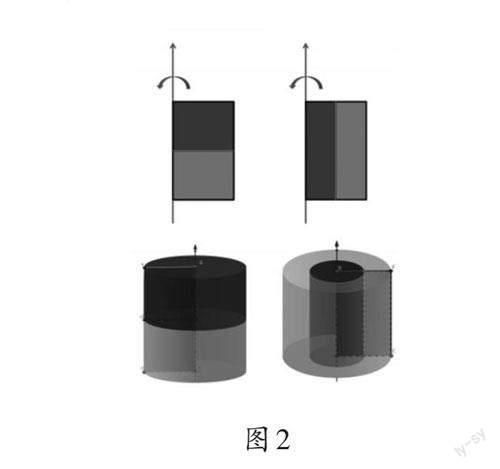
(教师根据学生的反馈,实时用动态数学软件演示将平面图形旋转成立体图形,如图2所示。师生讨论后发现,这两个长方形离旋转轴的位置与距离不相同,离旋转轴越远,旋转一周后得到的立体图形的体积越大。根据底面小圆半径∶大圆半径=1∶2,得到小圆面积∶大圆面积=1∶4,进而得到小圆面积∶环形面积=1∶3,而它们的高又相等,所以V圆柱∶V环柱=1∶3。)
生:按对角平均分,旋转一周后得到的是一个圆锥和圆柱去掉圆锥剩余的部分,它们的体积是相等的。
(教师根据学生的反馈,实时用数学动态软件演示将平面图形旋转成立体图形,如图3所示。)
师:为了称呼方便,我们把一个圆柱去掉等底等高的圆锥剩余的那个立体图形,叫作“余锥”。你的意思是它们的体积相等,也就是V圆锥∶V余锥=1∶1 ,是吗?
生:我认为圆锥和余锥的体积不相等。虽然旋转前这两个三角形是相同的,但是它们离旋转轴的位置和距离不一样,所以它们的体积不相等,感觉余锥的体积更大一点,但几比几我不知道怎么算。
设计意图:学生通过观察平面图形,想象平面图形旋转后形成的立体图形,重点思考圆锥、余锥、圆柱体积之间的关系。在教学中,教师充分利用信息技术,让学生在动态数学软件中直观看到二维平面图形是如何经过旋转形成三维图形的。在图形的变换中,学生发现旋转体的体积大小既和平面图形的面积大小有关,也和平面图形与旋转轴的距离远近有关。同时,信息技术也激发了学生的想象力,有利于学生积累空间想象经验。
(三)做思结合,验证想象
让学生经历“问题—想象—实验”的学习路径,带着问题通过想象进行实验操作活动,将脑中的想象与现实图像进行比较,既能验证实验过程,又能提升学生的想象水平。
师:我们想的到底对不对呢?有没有什么办法来验证?
生:用橡皮泥分别捏出一个圆锥、余锥、圆柱,然后比一比就可以知道了。
生:如果有一个空的圆锥、余锥和圆柱,我们就可以通过做模型进行比较。
在师生讨论交流的基础上,教师提供如下实验材料:透明圆柱、圆锥模具和太空沙(建议选用微珠型,容易塑形和保形)。学生带着问题,用太空沙分别制作圆锥、余锥、圆柱的立体模型,然后比较它们的体积。有的学生把余锥模型重塑成圆锥模型,发现1个余锥模型可以做成2个圆锥模型;有的学生把圆锥模型倒入圆柱模具,发现需要倒3次……在实验操作中,学生还提出,除了用太空沙做模型进行验证外,还可以用倒水的方法来验证。在此基础上,师生总结概括出等底等高的三个立体图形的体积关系是:V圆锥∶ V余锥∶ V圆柱= 1∶2∶3(如图4)。
设计意图:在实验操作中,学生对比了倒水验证与模型验证两种方法,发现:用倒水验证能快速知道等底等高的圆锥和圆柱之间的体积关系,但无法对圆柱体积的[23]形成概念;用模型验证能够清晰地看到圆锥、余锥、圆柱这三个立体图形,尤其是能对余锥有直观感知。学生经历“问题—想象—实验”的学习过程,从视觉、触觉两方面提高想象水平,从而不只从数量关系上认识到圆锥、余锥、圆柱的体积比是1∶2∶3,还联结了物体的形,深化了三者体积关系的表象。
(四)观察猜想,拓展想象
虽然学生掌握圆锥体积公式就已经达成了知识学习的要求,但是他们的想象力却还可以得到进一步的提升。因此,在教学中,教师应基于学生的已有知识经验,结合观察,让学生从多个角度拓展想象,深度发展学生的想象力。
1.观察与想象:柱体与锥体的体积关系
师:我们已经知道了圆锥和它等底等高的圆柱的体积比是1∶3,在此基础上,我们可以提出哪些猜想呢?
生:圆锥与圆柱等底等高时,体积比是1∶3,是不是其他锥体和柱体的体积比也是1∶3 ?
(教师根据学生的反馈,用课件动态演示其他柱體和锥体的变化过程,如图5所示。)
2.观察与想象:图形的面积、体积关系
教师引导学生比较二维图形和三维图形的关系。在二维图形中,把一条边缩成一个点,形成的三角形的面积是长方形面积的[12 ](如图6)。在三维图形中,把一个底面缩成一个点,形成的圆锥的体积是圆柱体积的[13](如图7)。
生:这让我想到了《三体》中的四维空间。如果把三维图形放到四维空间里,那么这个锥体和柱体的体积比会不会是1∶4?
生:我觉得很有可能。把三维空间的图形变成二维空间的图形,等底等高的三角形与长方形的面积比是1∶2,那么把三维空间的图形延展到四维空间里,它们的体积比很有可能是1∶4。
生:我也觉得等底等高的圆锥与圆柱在四维空间中的样子和在三维空间中的不一样,但是体积比很有可能是1∶4,在五维空间中体积比是1∶5,在N维空间中体积比是1∶N 。
……
设计意图:引导学生在二维、三维、四维[3]乃至更高维等人类无法直接感知的空间里进行想象,促进学生想象力的提升。学生从问题与想象开始,经过探索获得新知,又产生新的问题和想象,不断循环,从而增强回路。
三、教后反思
在小学阶段,受旋转体相关知识的限制,圆锥的教学通常采用实验法。但实验教学也容易落入只是动手操作的窠臼,学生不知道为什么要做实验,也不知道做实验要解决什么问题。因此,本设计强调将问题前置,由问题引领实验方法、实验步骤和实验结果的分析。
教学中,在提出问题后,教师不急于让学生动手操作,而是引导学生进行观察与思考,让学生观察平面图形的形状与位置,想象平面图形是如何绕着旋转轴旋转的,想象旋转后的立体图形的样子,想象它们的大小,想象面积相等的平面图形旋转后的体积是否相等,等等。学生在充分想象的基础上,开始设计实验,选择材料,确定操作方法。在动手操作阶段,学生通过视觉、触觉等感官活动所产生的信息与想象进行互动,在形成清晰表象的过程中也提升了想象水平。那么,按照“问题—想象—实验”这一路径进行学习,学生对圆锥与圆柱体积关系的掌握程度以及空间想象水平的发展成效如何呢?
为此,笔者进行了对比实验。从本校六年级的六个班中,挑选了两个水平相当的平行班,分别实施教学:对比班按典型教法教学(按配套的《教学参考书》[4]教学),特点是重视圆锥与圆柱等底等高条件的比较,让学生在倒水倒沙的过程中发现体积之间的关系;实验班以想象力发展为主线进行教学,让学生从旋转体的形成过程开始,提出问题,观察与想象图形的运动,在实验中做出模型,验证想象,发现关系,进而形成新的想象。
同一天上午,同一位教师分别在两个班进行教学,并在当天下午对学生进行问卷调查[5],调查结果如表1所示。
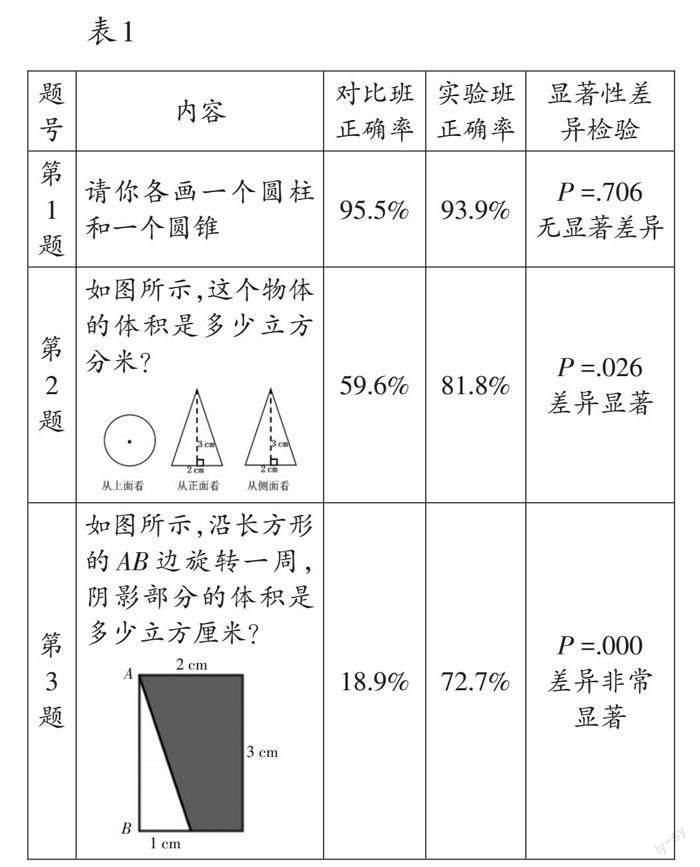
第1题要求学生画出指定的立体图形,学生看到图形名称要能想象出图形的形状。从结果来看,P >.05说明两种教法无显著差异。第2题要求学生能根据平面图形想象出特定的圆锥,并能正确选择相应数据计算体积。第2题要求的想象力水平明显比第1题要高,从结果看,.01< P <.05说明两种教法差异显著,但差异不是非常显著。在前两题中,无论是画图还是体积计算,学生想象的对象都是静态的图形,而第3题则需要学生动态想象,以运动的观点解决问题,从结果来看,P <.001说明差异非常显著。
当然,调查结果只能说明不同教法与想象力水平的相关关系,并不能说明因果关系。因为在实验过程中有许多不可控制的变量,比如学生看到动态数学软件中的动画会更加兴奋和专注,学生更喜欢玩太空沙因而对太空沙的塑形与变形印象更深刻等,这些因素都有可能对调查结果产生影响。但是,不可否认,以想象力发展为核心的“问题—想象—实验”这一学习路径,对学生知识的掌握、素养的发展都起到了积极的作用。本文只不过抛砖引玉,还期待更多的专家、教师来关心学生的想象力发展,并开展相关的实践活动,毕竟,想象力是人类独特的高级认知能力。
参考文献:
[1]武建军.审视“动手操作”与“数学实验”的分野[J].江苏教育,2017(9):28-30.
[2]郜舒竹.用运动的眼光看形体[J].教学月刊·小学版(数学),2013(5):18-22.
[3]唐军强.En空间中几个幾何体体积间的关系[J].高师理科学刊,2015,35(12):22-23,26.
[4]张天孝.九年义务教育小学实验教科书数学教学参考书:六年级下册[M].杭州:浙江教育出版社,2021:85-86.
[5]徐云鸿.小学高年段空间观念测评体系研究[J].数学教育学报,2019,28(5):9-13,97.
(1.浙江省杭州市胜利山南小学
2.浙江省杭州青少年活动中心)

