钢-UHPC轻型组合梁负弯矩区接缝抗弯试验

孔祥武，韩 玉，胡美韵，晏班夫

(1.广西路桥工程集团有限公司，南宁 530011；2.湖南大学 土木工程学院，长沙 410083；3.广西大学 土木建筑工程学院，南宁 530004)

0 引 言

钢板组合梁具有构造简单、 制造方便、 用钢量省、 全寿命周期性能优异、 绿色环保等优点[1], 能充分利用混凝土和钢材各自的力学性能[2], 这一结构质量轻、 节段运输便捷、 架设速度快、 适应保通要求高的路段, 可有效提升公路桥梁的建设品质。UHPC(ultra-high performance concrete, 超高性能混凝土)材料制作的构件结构自重较小、 设计自由度大、 力学性能好、 耐久性高、 符合可持续发展理念[3]。如果将钢板组合梁的混凝土桥面板用UHPC材料代替, 将大大降低组合梁的自重, 施工也可由常规方法(先架设钢板梁部分, 之后浇筑上部混凝土板)转变为先在已制作好的双钢板梁上浇筑UHPC桥面板形成单榀π型钢-UHPC组合梁, 之后进行整体架设。钢板组合梁桥面板部分UHPC化是未来城市、 高速公路中小跨径桥梁装配化、 工业化发展中的一个有益补充[4]。

钢-UHPC轻型组合梁中的预制单元一般具有较为稳定的品质, 因此单元之间的连接成为了决定桥梁质量的关键, 特别是支点负弯矩区的开裂及连接构造处理应重点关注。传统钢板组合梁桥中常见的负弯矩区裂缝控制措施包括加强配筋、 张拉预应力束以及优化施工工艺等。通过强配筋阻裂是最为传统的设计思路, 但过密的配筋会影响混凝土浇筑质量。张拉预应力束也是常用的钢混组合结构负弯矩区处理方法[5], 但纵向预应力通过栓钉传递至钢梁会降低桥面板预应力施加效率。此外, 中支点顶升法及调整混凝土浇筑顺序等施工优化方法也可作为改善负弯矩区受力的辅助措施[6], 其本质是使负弯矩区混凝土中储备一定初始压应力以降低使用阶段混凝土的开裂风险, 但这类方法效率较低且施工较为复杂。在德、 法等欧洲国家, 较为常见的一种钢混组合结构负弯矩区处理方法是设置墩顶横梁接缝[7], 施工时先架设预制组合梁于墩顶临时支撑上, 待全桥架设完成后, 施工墩顶横梁, 完成简支到连续的体系转换。学者们对这类钢板组合连续梁桥负弯矩区横梁接缝的构造设计、 受力性能、 抗震性能等进行了系列研究[8-10]。在UHPC材料在钢板组合梁的应用方面: 邵旭东等[11]提出在普通钢板组合梁桥横向接缝中引入UHPC材料以解决负弯矩区混凝土易开裂的问题; 邓舒文等[12]提出一种在整体预制钢-UHPC组合梁两端设置端隔梁, 并现浇阶梯型UHPC接缝的负弯矩区处理方案。研究表明, 将UHPC材料应用于钢板组合梁桥面板, 可进一步减小桥面板尺寸、 降低结构自重, 实现整体预制、 快速架设, 将UHPC应用于组合梁负弯矩区, 则可充分发挥材料的抗拉性能, 改善负弯矩区受力并大大简化施工工艺。

本文提出了一种预制钢-UHPC轻型组合连续梁桥结构, 设计了适用于该组合梁墩顶负弯矩区的横向接缝构造, 通过强配筋及现浇UHPC材料的方式提高负弯矩区阶梯状T型湿接缝的抗弯、 抗裂性能。以云南省昌保高速公路某跨线桥为依托工程, 对组合梁负弯矩区节段进行1∶2缩尺模型抗弯加载试验, 研究了负弯矩区UHPC湿接缝的抗弯破坏模式及承载力计算方法。

1 工程背景

依托工程桥型布置及组合梁一般构造, 如图1所示, 该桥采用3×30 m钢-UHPC轻型组合连续梁结构, 横向由两榀单宽4.0 m的钢-UHPC预制π梁组成。单榀组合梁由2片相距2 m的工字钢板梁与其上通过钢栓钉连接的UHPC桥面板组成, 工字型钢梁高115 cm, UHPC桥面板厚12～20 cm, 跨中全梁高135 cm。

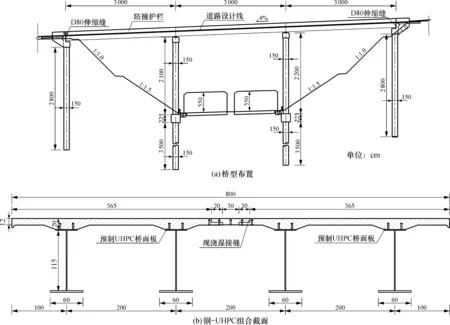
图1 钢-UHPC组合桥型布置(a)与截面尺寸(b)Fig.1 Bridge layout(a) and section dimension(b) steel-UHPC composite bridge

如图2所示, 在相邻两跨钢-UHPC预制梁的墩顶设置1.2 m宽的混凝土横梁接头, 该区域钢梁无上翼缘, 腹板以墩顶中心线为对称轴进行U型开槽, 伸入横梁的工字钢腹板部分设置有PBL连接键, 钢下翼缘部分则布置有栓钉; 距墩顶中心线600 mm处横梁端部设置有与上、 下翼缘及腹板焊接的端承压板, 其上布置侧立栓钉埋设在混凝土横梁内; 预制π梁吊装后(混凝土横梁浇筑前), 相邻工字钢下翼缘及腹板在端部进行错位施焊连接。

图2 现浇接缝构造图(单位: mm)Fig.2 Structure diagram of cast-in-situ joint

预制组合梁拼接后, 横梁接头分两次浇筑。第一次浇筑C50普通混凝土至距桥面30 cm高处, 达到强度后, 结构由简支体系转换为连续体系, 然后进行第二次的UHPC浇筑。为提升抗裂能力、 防止横梁端部断面裂缝贯通发展, UHPC湿接缝部分增加了水平台阶, 接缝立面呈T型条带形式, 该条带纵桥向长600 cm, 厚7 cm, 主要承受成桥后的活载作用。

2 模型试验方案

2.1 模型设计

为研究横向接缝在负弯矩下的受力情况与破坏模式, 取实桥负弯矩区10 m长度范围内的半榀π梁为研究对象, 按相似比原则设计了1∶2缩尺模型, 如图3、 4所示。试验梁总长5.0 m、 计算跨径4.8 m、 高0.678 m, 模型中心0.6 m范围内为横梁, 横梁左右各1.2 m范围为面板加厚位置, 普通及加厚截面翼板厚度分别为6、 10 cm, 混凝土翼板宽度为100 cm。另在加载位置设置2道12 mm厚加劲肋防止加载点截面屈曲, 模型下部工字钢采用Q345钢板焊接而成。缩尺模型中的栓钉布置与实桥保持刚度等效, 横截面钢筋与实桥主筋配筋率一致、 形心位置相似。

图3 试件设计尺寸图(单位: cm)Fig.3 Design detail of specimen

图4 试件构造图(单位: mm)Fig.4 Elevation of transverse beam joint of specimen

2.2 模型制作

预制梁桥面板UHPC材料胶凝成分包括水泥、 机制粗砂(粒径1～2.36 mm)、 机制细砂(粒径0～1 mm)、 硅灰、 矿粉、 水、 高效减水剂, 各材料配比为1.00∶0.70∶1.00∶0.22∶0.15∶0.24∶0.02; 而钢纤维直径0.2 mm、 长度13 mm、 体积掺量为2%; 机制砂采用云南保山当地白云岩加工得到, 其中细集料达到了《建设用砂》(GB/T 14684—2011)规定的优等品指标[13]。测得UHPC拌合物扩展度为640 mm, 流动性满足施工要求。现浇接缝用UHPC材料钢纤维体积掺量为2.5%, 采用自然养护方式。表1给出了UHPC材料性能指标。

表1 混凝土材料力学性能

2.3 加载方案与测点布置

采用将试件倒置的方式进行四点加载抗弯试验, 加载装置如图5所示。普通混凝土横梁位于试件纵向中点至两端各0.875 m范围的加载纯弯段内, 如图6a所示, 横梁两侧刚度突变的A—A截面、 上层UHPC接缝条带与预制段交界处的B—B截面为重点关注区域。此外, 跨中截面C—C、 纯弯段内截面D—D及B—B截面附近的E—E截面也一并进行测试。A—A截面关于跨中对称截面标识为A′—A′, 其他截面类推。对上述截面中钢筋、 钢梁的上下翼缘及腹板、 UHPC板顶面及侧面进行应变测试, 测点布置如图6b所示。加载过程中, 分别采用百分表与裂缝观测仪测量结构挠度及UHPC板表面裂缝宽度。采用单调分级加载方式, 初期每级控制荷载为25 kN, 达到650 kN后, 采用位移控制加载方式, 每级0.5 mm。

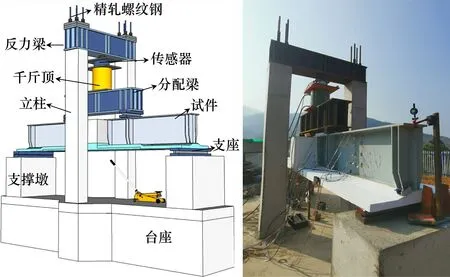
图5 加载装置Fig.5 Test set-up

图6 应变测点布置图(单位: mm)Fig.6 Layout of strain gauges

3 破坏形态及试验现象

3.1 破坏形态

试件破坏形态如图7所示, 主要表现为A—A截面UHPC板发生纵向拉裂破坏, UHPC板被彻底拉开, 其中钢筋也已破断; 横梁混凝土在钢梁端承压板及腹板的拉扯下出现贯通斜裂缝且伴有分层剥落现象; 弯剪段钢梁腹板可见明显剪切变形。而预制部分UHPC由于设置了水平抗剪钢筋且前期凿毛到位, 因此与顶部现浇UHPC连接较为紧密, 后期试验梁破坏未完全沿新旧UHPC界面开展。

图7 破坏形态示意图Fig.7 Schematic of failure patterns

3.2 破坏现象及裂缝分布

试验梁的破坏及裂缝分布情况如图8所示。加载过程中观察到的试验现象描述如下: 荷载加至0.17Pu时(试验梁极限荷载Pu为1 824 kN), 纯弯段内出现首条裂缝, 随着荷载增加, 各截面附近陆续出现多条宽度不超过0.05 mm的微裂缝, 由以往研究成果[14]可知, 此时的微裂缝对结构承载及耐久性能无明显影响; 0.28Pu之后, 横梁顶部开始出现裂缝, 且既有裂缝宽度逐渐超过0.05 mm; 加载至0.36Pu时,B—B截面顶部出现一贯通整个UHPC面板的细直裂缝, 之后, 新裂缝出现的增势趋缓, 既有裂缝的长度及宽度则不断增长; 加载至0.82Pu时,A′—A′截面UHPC板表面最大缝宽达到0.2 mm; 继续加载, 在A—A截面顶部, 有一条在651 kN(0.36Pu)时开始出现的裂缝突然扩展成为主裂缝, 之后裂缝数量基本不再增加, 但缝宽扩展速率明显加快; 加载至0.92Pu时, 横梁端承压板旁混凝土表面可见多条裂缝开展,A—A截面最大裂缝宽度超过5.0 mm, 由文献[15]可知, 此时裂缝处钢纤维从UHPC基体中拔出, 截面承载能力迅速下降; 荷载达到Pu后不久, 随着一声巨响,A—A截面钢梁以上UHPC板完全断开, 钢筋拉断, 试件破坏。

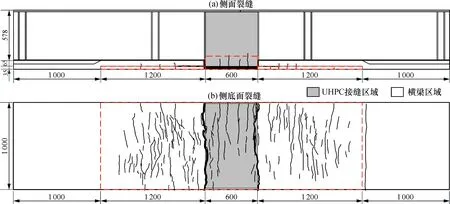
图8 UHPC板裂缝分布图(单位: mm)Fig.8 Crack distribution of UHPC specimen

图9为加载过程中UHPC板最大裂缝宽度达到0.2 mm之前的荷载-裂缝宽度曲线。裂缝刚出现时扩展速度较为缓慢, 在裂缝宽度从刚出现到发展至0.2 mm的时间段内, 荷载-裂缝宽度曲线基本呈线性关系。之后裂缝迅速扩展, 荷载-裂缝宽度曲线呈非线性发展, 加载至1 671 kN(0.92Pu)时, 最大裂缝宽度已超过5.0 mm。

图9 UHPC板荷载-最大裂缝宽度曲线Fig.9 Load-main crack width curve of UHPC specimen

4 试验结果分析

4.1 荷载挠度曲线

根据试验加载现象、 应变测试数据及荷载-挠度曲线, 可将钢-UHPC组合梁受力过程划分为图10所示的4个阶段: ①弹性阶段(0～529 kN): 从开始加载至0.29Pu, 跨中挠度随荷载增加均匀线性增长, 期间裂缝宽度均未超过0.05 mm, 荷载-挠度曲线呈线性关系, 组合梁工作性能良好; ②弹塑性阶段(529～1 532 kN): 随着加载级数增加, 裂缝宽度逐渐增大, 纯弯段内D—D截面钢梁底板一侧屈服, 挠度变化速率加快, 荷载-挠度曲线开始呈非线性增长, 不断有新裂缝出现且裂缝扩展速率加快, 受拉钢筋逐渐屈服; ③破坏阶段(1 532～1 824 kN): 荷载加至0.84Pu时,D—D截面钢梁底板两侧均已屈服,A—A、C—C、A′—A′截面受拉钢筋陆续达到屈服强度, 钢梁变形急剧增大, UHPC板中钢纤维拔出声密集; ④下降阶段(荷载范围1 824～1 735 kN): 达到极限荷载1 824 kN后, 跨中挠度随承载力下降仍能继续增大, 之后荷载突然大幅掉落, 试件中受拉钢筋完全破断, 横梁中混凝土崩裂剥落。

图10 钢-UHPC组合梁荷载-挠度曲线Fig.10 Load-deflection curve of steel-UHPC composite beam

另由荷载-挠度曲线可计算得到试验梁的位移延性系数μd, 该值用来表征构件破坏前的非弹性变形能力, 本文取μd为构件破坏时的跨中位移Δu与变形发生明显转折时的位移Δy之比。由试验值得到μd=3.26, 结合文献[16]中的评价标准可知, 结构延性较好。

4.2 荷载应变曲线

由于结构对称, 仅示出模型一侧A—A～E—E截面钢梁底板及钢筋应变随荷载变化的情况。图11a为各截面钢梁底板应变变化曲线, 达到极限荷载时,D—D截面钢梁底板最先屈服,A—A次之,C—C截面接近极限荷载才屈服,E—E与B—B截面未屈服。分析可知, 虽然模型纯弯段内所受弯矩大, 但C—C截面中性轴以下混凝土可与钢梁底板共同受压, 从而减小钢梁中的应力并延缓其屈服进程;A—A截面得益于横梁及端承压板的约束作用, 不至于过早屈服;D—D截面则为距接缝较远且受接缝影响较小的一般截面, 其钢梁底板在加载至1 501 kN时就已屈服。

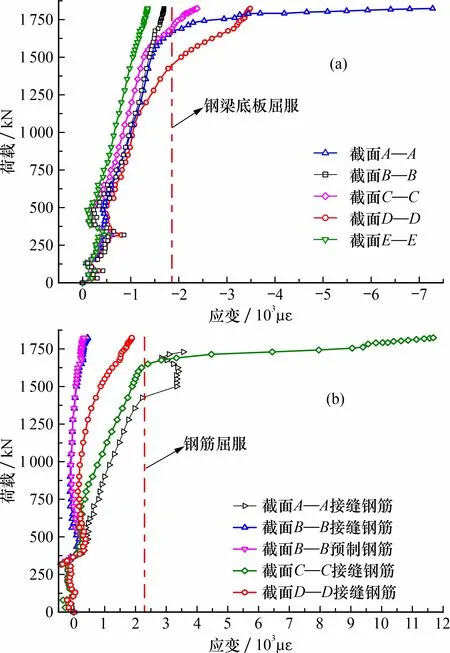
图11 钢梁底板(a)和UHPC板中顶层钢筋(b)荷载-应变曲线Fig.11 Load-strain response curves on the bottom of steel beam(a) and the top layer of UHPC slab of steel rebar(b)

对于受拉钢筋的应变变化, 由图11b可知, 截面B—B现浇部分与预制部分中的钢筋绑扎后并未屈服且应变十分接近, 说明钢筋在该处绑扎后共同受力; 另外, 截面D—D上层受拉钢筋在达到极限荷载时才接近屈服, 而截面A—A与C—C中的钢筋则分别于加载至1 355与1 550 kN时就已屈服。由截面A—A的破坏模式分析可知, 极限状态下该截面抗弯承载能力主要由受拉区后浇UHPC板、 板内钢筋、 端承压板(通过栓钉嵌入普通混凝土横梁), 以及受压区钢底板及部分钢腹板(U型开槽对钢腹板有削弱)提供, 因此A—A截面抗弯承载能力弱于C—C与D—D截面, 这也是其受拉钢筋先行屈服的原因。

4.3 截面应变分布

组合梁纯弯段内各截面纵向应变在不同荷载下沿梁高分布情况如图12所示。D′—D′截面较好地符合平截面假定, 前期纵向应变沿梁高呈线性分布且随荷载增大均匀增加, 中性轴位置基本不变。截面A—A、A′—A′由于位置与横梁两侧的端承压板邻近, 钢梁顶底板变形受到约束, 因此底板压应变与顶板拉应变均较平截面假定对应值有所减小。另外, 通过破坏形态可知,A—A截面一侧的钢梁从横梁内拔出的破坏程度强于A′—A′截面一侧, 因此其同侧D—D截面UHPC板中的拉应力会随着A—A截面已有裂缝缝宽加大得以释放, 后期D—D截面UHPC板中拉应力较小, 其中性轴位置随加载过程有向UHPC板方向移动的趋势。

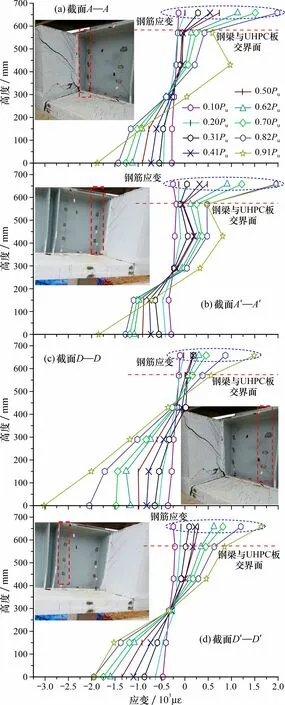
图12 各截面纵向应变沿梁高的分布Fig.12 Strain distribution along the height of different sections

5 抗弯承载力计算

由模型试验的破坏形态可知, 破坏界面从A—A截面的UHPC板开始并延伸至混凝土横梁与钢梁通过栓钉锚固连接的薄弱面, 横梁内混凝土发生锥体破坏。根据上述破坏形式用简化塑性理论分析结构的抗弯承载力计算方法, 可简单实用地计算组合梁极限抗弯承载能力。在简化塑性理论方法中, 假定钢材在受拉和受压时均达到屈服强度, 这与承载能力极限状态下组合梁的实际受力状态较为吻合[17]。

此外, 计算中还有以下说明: 1)分析中考虑了钢纤维在UHPC开裂后的“桥接作用”, 即计算承载力时计入UHPC的抗拉强度, 新旧UHPC结合处由于钢纤维不连续, 不计入该处UHPC的抗拉性能; 2)不计腹板开槽高度内的抗弯作用, 由于两片钢梁拼装时腹板仍有部分连接且钢梁底板焊接, 因此腹板连接部分可受拉或受压, 钢梁底板受压; 3)对于与横梁连接的端承压板, 其上所焊栓钉在混凝土横梁内可产生一定锚固拉力, 中性轴以下端承压板与混凝土横梁接触部分可传递混凝土中的压力。

图13为横梁与预制组合梁连接截面的塑性抗弯承载力计算图示, 计算中考虑了现浇UHPC条带拉力Ncr1、 钢筋拉力Nrt、混凝土体在栓钉作用下的抗拔承载力Ncb、 腹板拉力Nwt、 腹板压力Nwc、 混凝土压力Ncc、 钢梁底板压力Nsb对抗弯承载力的贡献。

力的平衡关系为

图13 钢-UHPC组合连续梁负弯矩区横梁接头抗弯承载力计算图示Fig.13 Flexural capacity of beam joint in negative bending moment zone of steel-UHPC composite continuous beam

Ncr1+Nrt+Ncb+Nwt=Nwc+Ncc+Nsb;

(1)

由此得到中性轴位置, 并对中性轴取矩, 得到抗弯承载力计算公式

Mpl=Awtfsyy1+Ncby2+Artfryy3+Au1fcr1y4+

Accfcy5+Awcfsyy5+Asbfsyy6。

(2)

其中:Mpl为横梁与预制梁连接截面抗弯承载力;fc为C50普通混凝土轴心抗压强度;fsy为钢板屈服强度;fcr1为由抗折强度, 根据文献[18]换算得到的现浇UHPC抗拉强度, 取6.33 MPa;fry为钢筋屈服强度;Awt、Art、Au1、Asb及y1、y3、y4、y6分别为钢腹板受拉区、 UHPC中钢筋、 现浇UHPC、 钢梁底板截面面积及对应截面形心至中性轴距离;Acc、Awc为受压混凝土及受压腹板截面面积;y5为Acc、Awc对应截面形心至中性轴距离;y2为Ncb至中性轴距离;hwt为腹板受拉区高度, 可通过式(1)所示力的平衡关系计算得到hwt。

混凝土体在栓钉作用下的抗拔承载力Ncb可根据欧洲广泛使用的CCD (concrete capacity design)法[19]进行计算, 该方法由大量试验数据回归分析得到, 假设混凝土破坏模型如图14所示。其中,hsc为栓钉埋入混凝土深度(mm);k为栓钉头厚度(mm);hef为有效埋深(mm), 其中hef=hsc-k。CCD法假设混凝土破坏体为四棱锥, 破坏体的立面投影中破坏面与基底呈35°角, 水平面投影则是一以栓钉为中心、 3hef为边长的矩形。

图14 混凝土抗拔承载力计算示意图Fig.14 Failure projected area calculation

(3)

其中:ncon, w为栓钉个数;d为栓钉直径(mm);fu为栓钉极限抗拉强度(N/mm2),fu取1.9fy与800 N/mm2中的较小值。

当抗拉强度由混凝土崩裂强度决定时,

(4)

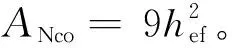
最终根据上述方法计算得到试件抗弯承载力Mpl=1 117.21 kN·m。

以上计算中的假设情况记为情形1。此外, 对于A—A截面的破坏, 本文还对以下两种情况进行了抗弯承载力计算(情形2、 3)。情形2: 忽略端承压板栓钉提供的抗拉锚固力, 其他条件与情形1一致; 情形3: 认为A—A截面的破坏发生在端承压板外的钢梁一侧, 按一般组合截面进行抗弯承载力计算, 计算图示见图15, 计算结果对比如表2所示。与试验值Mpl, t=1 390.8 kN·m相比, 情形1计算结果略小, 部分原因是尽管下层UHPC接缝凿毛到位, 计算中按常规做法不计接缝处UHPC抗拉能力, 所得结果较为保守; 情形2计算不如情形1准确, 说明栓钉嵌入混凝土横梁的抗拉锚固力不可忽略; 情形3计算值大于试验值, 说明假设条件不能很好地反映A—A截面极限状态下的实际受力情况, 计算结果偏不安全。综上所述, 按情形1进行抗弯承载力计算最为合理。

表2 试件抗弯承载力计算方法比较

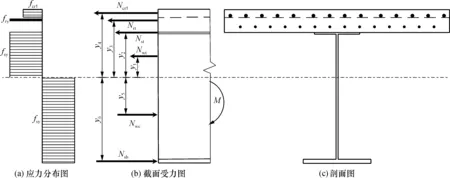
图15 情形3抗弯承载力计算Fig.15 Calculation of flexural capacity for Case 3

6 结 论

(1) 提出了一种预制钢-UHPC轻型组合梁结构, 设计了适用于该组合梁墩顶负弯矩区的横向接缝构造, 通过强配筋及现浇UHPC材料的方式改善了负弯矩区阶梯状T型湿接缝的抗弯、 抗裂性能。

(2) 试验表明, 带横梁接缝钢-UHPC组合梁的受弯破坏过程可分为弹性阶段、 弹塑性阶段、 破坏阶段及下降阶段共4个阶段, 结构具有较好的延性与承载性能。

(3) 根据负弯矩区接缝结构缩尺模型的受弯破坏形态, 提出了适用于接缝界面破坏的结构塑性抗弯承载力计算方法, 可偏安全地计算该类带横梁接缝钢-UHPC组合梁的负弯矩区抗弯承载力。

(4) 负弯矩区接缝构造中预制梁与现浇UHPC之间的连接至关重要, 钢梁与横梁之间的连接也对最终破坏形态有较大影响, 将来的工程应用中可对上述连接位置进行优化以提高抗弯承载力。