确定与不确定方法组合下的玉林市农业需水量区间预测
曾彦欣,钟献词,刘 芳
(1.广西大学 a.土木建筑工程学院;b.数学与信息科学学院,南宁 530004;2.中国能源建设集团广西电力设计研究院有限公司,南宁 530007)
0 引 言
水是人类生存发展不可或缺的重要资源, 是保证社会经济发展的基础。随着社会的不断发展和进步, 人类对水的需求量逐渐增大, 水资源短缺和分配不均成为制约社会、 经济、 环境可持续发展的重要因素。在全球水资源短缺的现状下, 科学地对城市需水量进行预测, 对有效解决社会水资源短缺及合理分配具有重要意义。
国内外开展了大量对需水量的预测研究。Zhou等[1]利用自适应学习算法提出了一种短期需水预测模型; Yasar等[2]基于多因素对用水量影响建立了多元非线性需水预测模型; Felfelani等[3]利用人工神经网络对城市用水量预测进行了研究; Abu-Mahfouz等[4]建立了可减少用水损失的需水预测模型以及针对供水管网压力管理与漏损区域识别的预测模型; 付强等[5]利用神经网络模型对水稻的灌溉需水量进行了预测; 王景雷等[6]基于DEM提出了针对冬小麦的需水预测模型; 张清周等[7]建立了基于信息粒化的支持向量机预测模型,能够较好地实现城市短期(最高) 时用水量的预测。此外, 为了发挥不同算法的优势, 寻求更好的预测效果, 一些学者将多个算法组合,来预测需水量, 如:章恒全等[8]结合灰色关联分析与神经网络对江苏省需水量进行了预测; 宋帆等[9]将聚类方法和灰色关联分析相结合, 对吉林省用水量进行了预测;韦文渊等[10]采用用水定额等方法计算了柳州市生产生活、生态环境及生态市建设等的需水量。还有一些学者改进了已有的预测方法, 如查木哈等[11]利用BP神经网络建立了双层隐层模型, 陈磊[12]构建了基于ν-SVM的需水量预测模型, 得到了更精确的结果。
综上, 上述研究均属于考虑确定性方法的点预测, 而实际水资源的分布及利用充满着不确定性, 点的预测值不能准确表达这些不确定性, 因此考虑不确定方法的区间预测更符合实际情形。郭强等[13]提出了基于贝叶斯准则的BP神经网络需水预测模型; 杨利纳等[14]利用灰色关联分析和遗传算法优化BP神经网络对校园需水预测区间进行了研究; 吴泽宁等[15]运用定额法、 回归分析法和系统动力学方法得出各自的确定性需水预测结果后, 将最大、 最小值分别取为区间的上下限, 再随机生成数据进行正态检验, 若随机数不符合正态分布则对随机数进行正态转化后计算95%置信区间, 并对郑州市工业需水量作出了估计。
本文以玉林市农业需水预测为研究对象, 提出了结合定额法、 趋势分析法、 BP神经网络模型、 灰色模型、 ARIMA模型5种确定性预测方法以及统计分析的不确定性区间预测方法, 获得了玉林市2030年农业需水区间预测结果, 为该地区的水资源优化配置及评价方案构建提供一定的参考。
1 研究区概况
玉林市地处广西东南部, 全市多年平均水资源量为116.89亿 m3, 人均水资源量仅为2 065 m3, 在广西全区14个地级市中排名末位。2019年, 玉林市GDP在全区14个地级市中排名第4, 玉州、 北流、 福绵一体化城市及周边土地面积约2 130 km2, 约占全市土地面积的17%, 耕地面积约7×104hm2, 约占全市耕地面积的32%, 但该地区水资源量还不足全市的1/5, 可利用水资源量不足以支撑玉林市核心区域的经济社会发展。玉林市2019年农林牧渔业总产值为546.8亿元, 第一产业生产总值指数为103.6%, 年总用水量为24.2亿 m3, 其中农业灌溉用水量为16.75亿 m3。2009—2019年玉林市农业灌溉用水总量及农林牧渔业总产值见表1。
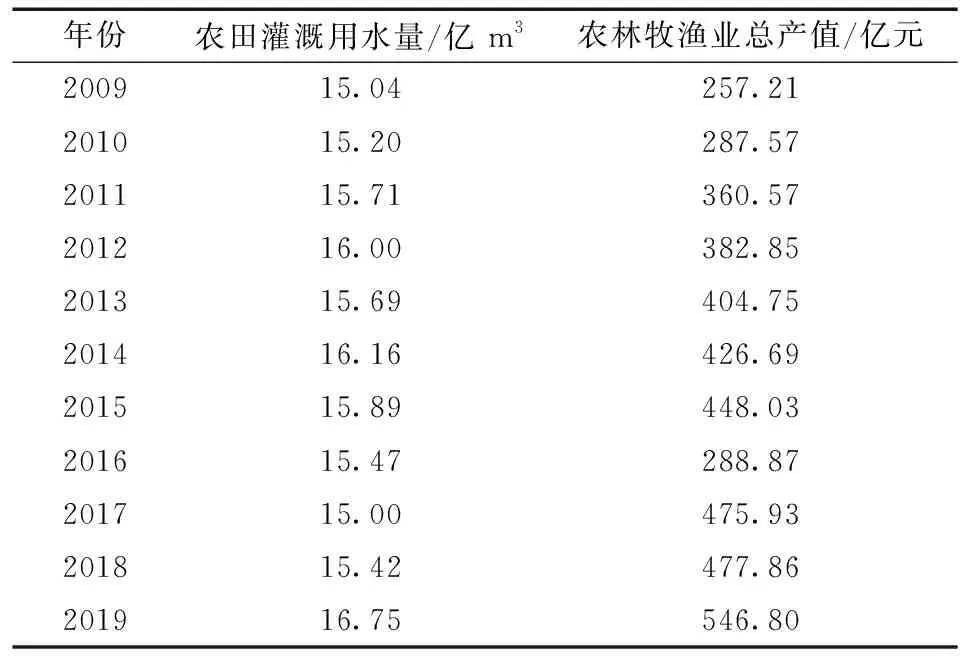
表1 2009—2019年玉林市农田灌溉用水量及农林牧渔业总产值
根据《农林牧渔业及农村居民生活用水定额》(DB45/T 804—2019)及《玉林市水资源综合规划(2016—2030)》, 采用保证率p=75%时各类作物灌溉定额、 灌溉水利用系数和各类作物灌溉面积, 见表2; 依据《玉林市养殖水域规划》《玉林市水资源综合规划(2016—2030)》《农林牧渔业及农村居民生活用水定额》(DB45/T 804—2019)确定规划水平年全市的鱼塘面积、 牲畜数量以及渔畜业用水定额, 见表3。

表2 2020、 2030年玉林市农田灌溉用水量定额指标
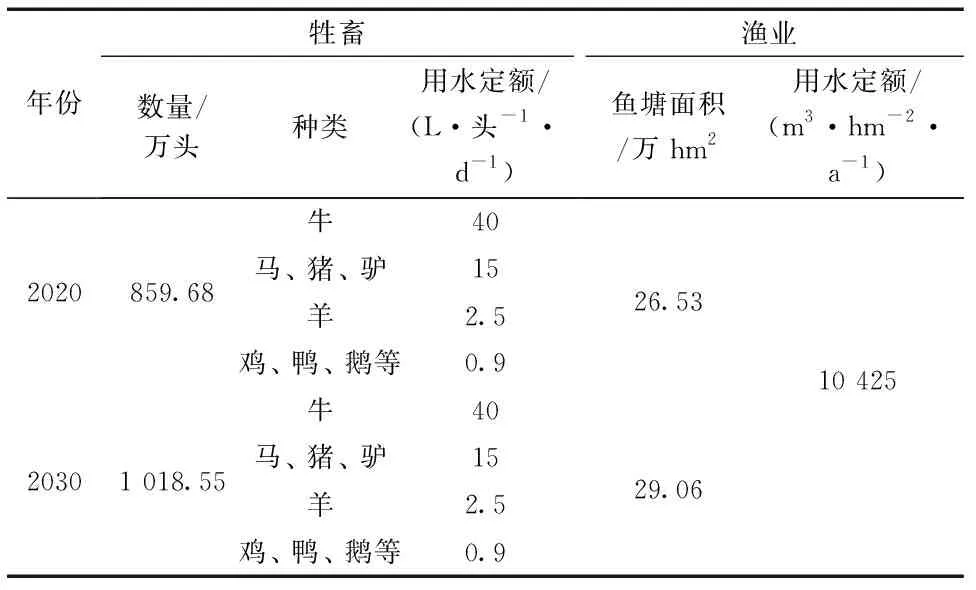
表3 2020、 2030年玉林市渔畜业用水量定额指标
2 研究方法
确定性方法给出的是点预测值, 但水资源调查和使用中不可避免地存在大量不确定因素, 点估计值与客观实际情况之间存在一定的不兼容性。基于不同方法预测结果的统计分析, 可在一定程度上改善单一方法造成的结果偏差。本文使用定额法、 趋势分析法、 BP神经网络模型、 灰色模型、 ARIMA模型5种方法组合以及统计分析对需水量进行区间预测。定额法采用经济社会发展指标和相应的定额预测需水量, 是需水预测中的常用方法。趋势分析法基于历史数据, 利用增长曲线进行拟合预测。BP神经网络模型不仅进行信号正向传播, 同时还进行误差的反向传播, 是一种具有自学习、 非线性和自组织、 大规模并行等优点的人工神经网络模型。灰色预测模型所需样本量少、 样本无需规律性分布, 且可以通过对时间序列进行分析和拟合、 估计出合适的模型系数, 从而进行数据预测。
2.1 定额法
使用定额法预测农田灌溉需水量需要3个重要因素: 各种类型作物的净灌溉定额、 灌溉水利用系数、 灌溉面积[15]。农田灌溉用水定额法的需水量[16]
Q农田灌溉=∑(ωiυi)/λi,
(1)
其中:Q农田灌溉为规划水平年农田灌溉需水量, 亿m3;i表示作物类型;ωi表示各类作物灌溉定额, m3/hm2;υi为各类作物灌溉面积, 万 hm2;λi为灌溉水利用系数。
参考DB45/T 804—2019, 渔业用水定额法的渔业需水量
Q渔业=∑(PiAi),
(2)
其中:Q渔业为规划水平年渔业需水量, 亿m3;i表示鱼的类型;Pi为养殖场年内单位养殖面积补水量定额, m3·hm-2·a-1;Ai为补水面积, hm2。
参考DB45/T 804—2019, 畜禽用水定额法的畜禽需水量
Q畜禽=∑(WiNiTi)/1 000,
(3)
其中:Q畜禽为规划水平年畜禽需水量, 亿 m3;i表示畜禽类型;Wi为各类牲畜、 家禽用水定额, L·只-1·d-1;Ni为养殖数量, 只;Ti为各类牲畜、 家禽生育期天数, d。
综上,Q农业需水量=Q农田灌溉+Q渔业+Q畜禽。
2.2 趋势分析法
采用趋势分析法预测农业需水量主要是通过对比时间序列上的农业需水量, 明确其变动增减的方向与幅度。在不同类型的趋势线中选择R2最大, 拟合程度最高的多项式曲线。
2.3 BP神经网络模型
BP神经网络的学习过程包括正向传播和反向传播, 分为输入模式顺传播、 输出误差逆传播、 循环记忆训练、 学习结果判别4部分。正向传播中, 输入信息经过输入层传递到隐含层, 经过函数计算后传向输出层; 若输出层未得到期望输出的结果, 则进行反向传播, 将误差信号返回, 根据修改各层神经元的权值和阈值调整误差, 直到误差小于期望值后才终止学习过程。
本文构建了一个3层的BP神经网络模型, 其中输入层节点数为3, 隐含层节点数为8, 输出层节点数为1, 期望均方差为1×10-3。通过主成分分析可知, 有效灌溉面积和粮食作物产量对农业需水量影响很大, 在分析农业需水量时具有重要意义, 因此将两者作为影响因素, 根据2007—2019年的有效灌溉面积、 粮食作物产量和农业用水量的数据对规划水平年2030年的农业需水量进行预测。
2.4 灰色模型
灰色模型是运用灰色系统理论研究部分信息已知、 部分信息未知的不确定性系统, 通过对已知部分的挖掘, 实现对演化规律的正确描述。本文使用的GM(1,1)模型是一阶一个变量的灰色预测模型, 可利用较少的数据预测较多的序列[18]。
2.5 ARIMA模型
ARIMA模型全称为自回归积分滑动平均模型(auto-regressive integrated moving average model), 是一种将非平稳时间序列转化为平稳时间序列, 通过确定模型的参数和阶数来进行时间序列预测的统计模型。ARIMA模型也记作ARIMA(p,d,q), 3个参数分别是时序数据本身的滞后数、 时序数据需要进行差分化的阶数和预测误差的滞后数。ARIMA用数学形式可表示为

(4)

2.6 正态检验与区间求解
将5种方法计算结果的最大、 最小值作为区间上下限, 使用RAND函数产生100个随机数, 并对所得的随机数进行正态检验。若随机数不符合正态分布则运用Minitab软件, 使用Johnson变换函数对随机数进行正态转化[14]。经检验确认, 转换后的数据符合正态分布X′~N(μ,σ2), 对转换后的数据进行95%置信区间的求解, 具体步骤如下:
①构造一个符合自由度为n-1的t分布的随机数列
(5)
(6)
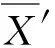
②根据给定的置信水平95%, 查t分布表得tα/2(n-1)值, 可对置信区间进行计算
(7)
在求得区间的上下限后, 可通过正态转换前后数据的关系式推求确定5种方法组合的95%置信区间预测值。
3 玉林市农业需水量区间预测
3.1 预测结果
利用定额法、 趋势分析法、 BP神经网络模型、 灰色模型和ARIMA模型预测玉林市2030年农业需水量, 结果见表4。

表4 2030年玉林市农业需水量预测结果
定额法是采用式(1)~(3)计算的各类需水量的总和。
趋势分析法根据趋势线方程预测玉林市规划水平年农业需水量
y=0.002 4x2+0.079 5x+15.403,
(8)
式中:y为农业需水量, 亿 m3;x为从2001年开始的时间序列号, 趋势线见图1。

图1 农业需水量趋势分析Fig.1 Analysis of agricultural water consumption trend
利用BP神经网络模型预测玉林市规划水平年农业需水量, 在迭代1 921次后达到理想效果, 误差为9.96×10-4, 2007—2019年农业用水量的预测值与实际值如图2。
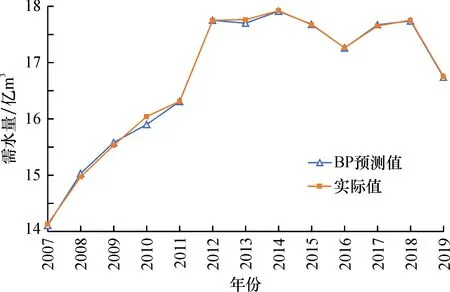
图2 2007—2019年农业用水量实际值与预测结果比较Fig.2 Comparison of actual and forecast values of agricultural water consumption from 2007 to 2019
利用灰色模型预测玉林市规划水平年农业需水量, 采用玉林市2001—2019年农业用水量数据建立模型, 计算结果的绝对误差为70.29%, 相对误差为0.04%, 小误差概率p>0.7, 且方差比c<0.65。
利用ARIMA模型预测玉林市规划水平年农业需水量, 采用2001—2019年的时间序列, 残差检验结果为194.49×10-2, 接近于2, 残差接近正态分布且相互独立。将19个数据用于训练, 运算结果落在95%置信区间, 2030年的预测值符合要求。
将以上5种方法的预测结果的最大、 最小值作为规划水平年2030年的玉林市农业需水量预测范围, 即2030年的农业需水量为16.34亿~19.95亿 m3。使用RAND函数产生区间内的100个随机数并进行正态分布检验。发现玉林市2030年的预测值区间随机数不符合正态分布, 故对它们进行正态分布转化
(9)
所得的随机数频率分布如图3所示。
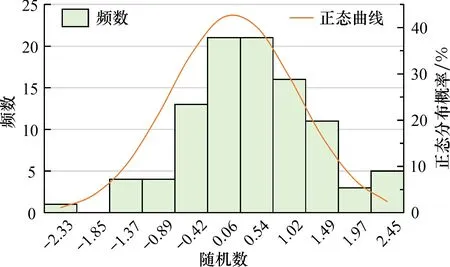
图3 2030年随机数频率分布Fig.3 Frequency distribution of random numbers in 2030
正态转换后的随机数呈现出正态分布特征,P值为0.912, 可知转换后的数据符合正态分布, 再进行95%置信区间求解, 计算结果见表5。

表5 2030年正态分布数据的置信区间
由式(9)中X′和X的对应关系可计算出玉林市2030年农业需水量预测值的95%置信区间为17.84亿~18.37亿 m3。
3.2 结果检验
为了验证方法的有效性和优越性, 组合定额法、 回归分析法和系统动力学法对玉林市2020年农业需水量预测值进行比较。定额法值根据式(1)~(3)进行计算。由回归分析法可知,粮食产量对玉林市农业用水量有较大影响,将其作为农业需水的影响因素,采用幂函数分析粮食产量随时间变化规律,拟合度为0.64。
Y=-0.002 5(lnX)3+0.142 3(lnX)2-
0.101 2lnX+11.727 8,
(10)
X=255.69x0.258 9,
(11)
式中:Y为农业需水量,亿 m3;X为粮食作物产量,万 t;x为时间(为减小误差,以1,2,3,…,22代替)。农业需水量SPSS回归分析显著性水平小于0.05,回归方程合理。
系统动力学法利用Vensim PLE软件建模模拟农业需水量[20]。Vensim模拟中一阶方程的基本形式为
LK=LJ+ΔTVKJ,
(12)
式中:LK、LJ为K、J时刻的状态变量;ΔT为时间间隔;VKJ为J时刻到K时刻的速率变化向量。
本文Vensim模型模拟年限为2010—2030年, 模拟步长设为1 a, 以2009年数据作为初始计算值, 初始农业总产值为257.21亿元, 初始农业灌溉面积为14.64万 hm2。为防止结果溢出, 建模时参考《玉林市水资源综合规划(2016—2030)》中2030年农业总产值为477.60亿元, 农业灌溉面积为16.14万 hm2。
模型中农业总产值Y与农业灌溉面积X随时间变化的变化规律由模型内置表函数决定
Y=WITHLOOKUP(X,{[(xmin,ymin)~(xmax,ymax)]}),
(13)
式中,x为时间,y为增长率。
采用定额法、 回归分析法和系统动力学法对2020年玉林市农业需水量的预测结果如表6所示。将3种方法计算的结果确定为农业需水预测范围,即15.96亿~20.73亿 m3,在区间范围内随机产生数据进行正态检验,结果表明随机数P值为0.015<0.05,因此,需对数据进行正态转化后计算其95%置信区间,得到2020年玉林市农业需水量的置信区间为18.027 3亿~18.697 6亿 m3。

表6 3种方法对2020年玉林市农业需水量的预测
使用本文的5种方法组合对2020年玉林市农业需水量的预测结果如表7所示。

表7 5种方法对2020年玉林市农业需水量的预测
将以上5种方法预测结果范围作为2020年玉林市农业需水量预测范围, 即17.15亿~20.73亿 m3, 通过正态检验及正态转化后计算其95%置信区间, 得到2020年玉林市农业需水量的置信区间为18.73亿~19.30亿 m3。根据《玉林市水资源综合规划(2016—2030)》, 2020年农业需水量的预测值为18.80亿 m3, 该数值在本文方法预测区间, 而不属于定额法、 回归分析法和系统动力学法组合计算的预测区间。通过比较说明, 本文使用的确定性与不确定性组合区间预测方法是可行的, 并具有一定的优越性。另外, 本文使用的BP神经网络考虑了需水量的影响因素, 具有一定基于系统动力学法考虑要素间的因果制约关系进行预测的优点, 同时通过不断迭代计算提高了结果精度。
综上, 由计算结果可知, 本文预测的区间有95%的可能包含了实际农业用水量, 预测值具有较高的预测准确性, 且在5种方法预测的需水量相差较大的情况下, 最终计算结果的区间范围较小, 说明本文提出的方法适用于区域的需水量区间计算, 并可后续的水资源配置提供科学依据。
4 结 论
(1)本文采用定额法、 趋势分析法、 BP神经网络模型、 灰色模型、 ARIMA模型5种方法进行玉林市农业需水量预测, 并利用置信区间估计理论进行不确定性预测, 结果表明, 在95%的置信水平下规划水平年2030年的农业需水量的置信区间为17.84亿~18.37亿 m3。与传统取最大最小值作为区间上下限的方法比较, 本文确定的置信区间范围更小, 提高了预测的精度。
(2)组合定额法、 回归分析法和系统动力学法3种方法应用于玉林市2020年农业需水量预测, 将其计算结果与本文方法计算结果进行对比, 本文的预测结果符合实际规划, 具有较高科学性和可行性。
(3)影响需水量的因素众多, 本文使用BP神经网络模型进行需水量预测时, 只是基于主成分分析法确定输入因素并建模, 对于因素输入的选择还可以进一步研究。另外, 样本的数据量较少, 在一定程度上限制了预测模型的精度, 今后也可尝试在更多数据的基础上, 考虑赋予不同预测方法科学的权重因子对需水量预测开展进一步的研究。

