复杂机坪运行模式下的停机位分配协同优化
刘禹汐,刘继新,田 文
(1. 南京航空航天大学 民航学院,南京 211106;2.国家空管飞行流量管理技术重点实验室,南京211106)
近年来,民航业发展迅猛且取得了重大成效,但仍然存在关键资源不足,基础设施保障能力面临容量和效率双瓶颈等问题.解决机位资源短缺问题通常对机场现有机位资源进行科学的预分配和实时调整,以提高机位资源的利用率、增强机场保障能力[1-2].
机位资源预分配阶段会受到多种因素限制,停机位分配方案作为运控人员基于机场、航空公司以及旅客三方利益的决策载体,传统的停机位预分配方法难以满足现实需要的协同决策[3].而我国民航运输运力主要分布在大型枢纽机场,航班流量较大,航司和旅客多样化显著,机坪运行态势复杂,集中特点明显,在机坪内部产生的运行冲突较多.因此针对这种普遍存在的问题,如何在保证航空器运行安全和充分利用机位资源的条件下实现大型枢纽机场停机位分配的多目标协同优化已经成为亟须解决的难题[4-5].
2010年,刘长有、翟乃钧[6]在兼顾系统运行安全和效率方面进行了有效的初步探索,将航班推出冲突作为安全性约束,建立了可以避免推出冲突的多目标停机位优化模型.2011年,刘长有[7]等在模型中加入避免潜在推出冲突的约束条件,建立多目标停机位分配模型,并采用遗传算法进行求解.2013年,Kim[8]等人以最小化乘客的步行时间、最小化飞机的滑行时间和最小化机位冲突的持续时间为目标建立了平衡三者的停机位优化模型,结果表明此优化方案在每个目标上都优于当前的分配方案.2014年,Prem[9]等人首次将乘客连接收入、区域使用成本、停机位调度的鲁棒性及其相关约束一起纳入多目标停机位指派模型中.2018年,徐思敏[10]等人为通过优化停机位分配方案来实现综合利益最大化,以航空公司运行成本、旅客步行距离、航班冲突概率综合最小化以及航空公司公平性最大化为优化目标,建立多目标停机位分配模型,并用NSGA-II进行高效求解.2019年,高阳[11]运用“安全关口前移”的思想,以最小化航班冲突次数和最大化航班靠桥率作为优化目标,设置同机位和相邻机位的最小安全时间间隔作为约束条件,建立随机扰动航班时刻下的停机位分配优化模型,运用改进的全局人工蜂群算法进行求解.同年,马思思[12]在建立滑行道和停机位联合调度模型时,考虑了停机坪推出、进位约束,对机位之间避免冲突发生要保持的最小安全时间间隔进行较为具体的计算,将其代入约束中.2022年,李龙海[13]等人建立双层规划模型,以最大化机场运行效率作为上层模型的优化目标,以同一停机位相邻航班推出冲突时间最少作为下层模型的优化目标,利用遗传算法进行求解,降低停机位运行风险.
从以上研究可以看出,在研究以航空器运行安全为重点的多目标停机位分配问题时,大部分学者仅仅对同一停机位、或相邻停机位之间的航班设置避免推出冲突的约束,少部分学者将最小化航班冲突作为优化目标,但是这两种方法都没有考虑机坪的实际运行规则,只针对相同或相邻机位航空器的推出进位进行限制,缺乏实际意义,得到的分配方案会增加运控人员实时分配停机位的工作负荷.目前,我国大中型机场广泛使用多指廊式的停机坪构型,港湾U型区数量较多.对于此类复杂机坪,通过停机位分配来保障运行安全的难点在于剖析航空器在港湾U型区域里的运行.U型区指的是两条平行指廊之间的停机坪以及滑行通道等站坪区域,其中的航空器自行滑入机位,借助牵引车顶推出位,并采用机头向内的方式停放.港湾U型区域一直是机坪盲区的聚焦点,其空间有限,停机位密集,运行模式较复杂,容易产生运行冲突,航空器与航空器、航空器与其他保障车辆等很容易发生刮蹭相撞的事故.因此为协同机场、旅客、航司三方的利益,兼顾机坪运行效率和运行安全,本文以武汉天河国际机场(以下简称“天河机场”)作为大型枢纽机场的典型案例,首先针对机场中主用客运机坪构型的运行方案进行分析,然后以最小化停靠在远机位的航班数量(即最大化飞机靠桥率)、最小化旅客步行距离以及最小化同机位航班冲突值作为目标函数,综合考虑复杂机坪的运行模式、航班对应运营区域的限制等符合实际情况的约束,建立多目标停机位分配协同优化模型,并采用适合该问题的多目标遗传算法——带精英策略的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ)对模型进行有效求解,最后结合天河机场的数据进行实例验证.
1 机场主用客运机坪构型运行方案分析
航站楼构型是制约机坪机位布局的关键因素.大型枢纽机场一般建有多座构型不同的航站楼,使得连接的机坪区域的空间结构和机位布局方式具有多样性,由此导致不同构型机坪下航空器的运行方案具有较大差异性.本文以天河机场为例进行不同构型机坪的运行方案分析.天河机场主用客运机坪构型如图1所示,包含5个港湾U型区域、1个港湾半U型区域以及1个直线型区域,其中港湾U型区域占天河机场客运主用保障机位的70%.

图1 天河机场整体布局
1.1 运行安全原则
1)在机坪内滑行道滑行时航空器前后机必须满足航空器地面滑行纵向间隔;
2)在机坪内滑行道滑行时航空器之间必须满足航空器地面滑行侧向间隔;
3)航空器在U型区内运行时,必须满足相应机型开车时的尾流安全间隔.
下面分别针对U型机坪和直线型机坪的运行模式进行分析.
1.2 U型机坪“双通道”运行模式
本模式下,根据民航规定航空器运行的相关间隔,将每个U型机坪分为“外”、“中”、“内”三个分区,U型区内两条滑行道看作一条滑行道使用,进离港航班均不允许与另一架U型区内航空器侧向交错滑行,以此确保航空器运行时满足各项安全间隔规定.图2为在双通道分区运行模式下,U型区的航班运行离港方式示意图.

图2 U型区航班运行离港方式
此方案中U型区内部顶端机位离港航空器直线向后推出,停止时姿态垂直于区域内滑行道.除U型区内其余机位离港航班就近推出至区域内滑行道,停止时姿态平行于U型区内滑行道机头朝港湾口方向.图2(A)表示每次只能在外区和内区各推出一架航空器,中区如有正在推出开车的航空器则内区、外区所处航空器不得推开.内区航空器推出到达指定位置后,两架航空器均可开车;图2(B)表示优先将中区的航空器推入内区后外区航空器才可推出,两架航空器均到达指定位置后方可开车.图2(C)表示优先将中区的推出的航空器拉入外区再推出内区航空器,两架航空器均到达指定位置后方可同时开车.
图3为在双通道分区运行模式下,U型区的航班运行进港方式示意图.当U型区内有航班正在开车,开车航空器区域往港湾口的相邻区域机位可以正常入位,进港航班机位不得与区域内正在运行的离港航班机位相邻.图3(A)表示当中区航班开时外区机位可以入位;图3(B)表示当内区航班开时中区、外区所有机位可以正常入位.而外区推开时停外区的进港航班需在港湾区域外的主滑上等待,待外区没有正在活动的航空器后方可入位.
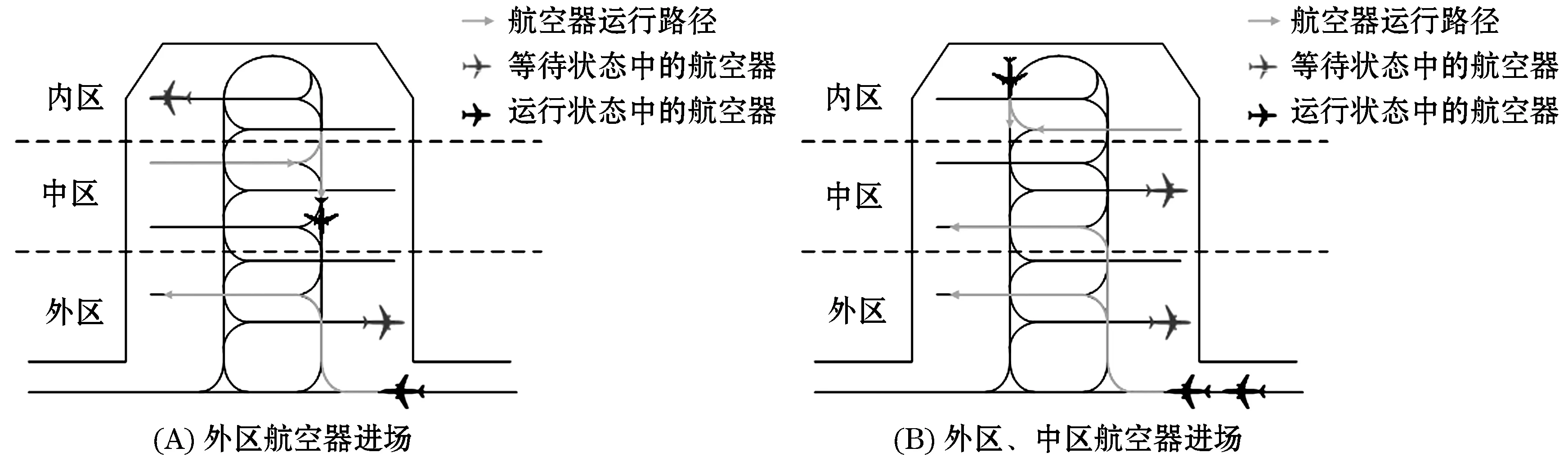
图3 U型区航班运行进港方式
1.3 直线型机坪运行模式
天河机场直线型机坪的运行模式相对来说比较单一,只规定了相邻机位的航空器禁止同时活动.
1.4 区域机位组合
根据上述分析的大型枢纽机场中存在的典型机坪构型和运行模式,本文提出“区域机位组合”的概念来表征不同机坪构型下的航空器进离港运行模式.基于机坪构型和机位、滑行通道的相对位置关系,将同一机坪区域内具有相同进离港滑行路径且受到规则限制彼此影响的若干机位视为一组,称为“区域机位组合”.同一区域机位组合中的停机位之间不能同时推出/进入航班,不同区域机位组合中的停机位之间互相不受约束.
2 多目标停机位分配协同优化模型
2.1 符号说明
见表1.

表1 模型符号说明
2.2 数学模型
从协同机场、旅客、航司三方利益和提升机坪运行效率及运行安全的角度出发,建立机场指标、旅客指标、安全指标等度量停机位综合效能,构建以下多目标停机位分配协同优化模型.
(1)
(2)
(3)
(4)
∀i∈F, ∀j∈F, ∀k∈G
(5)
(6)

(7)
(8)
G(Fa)⊆Ga
(9)
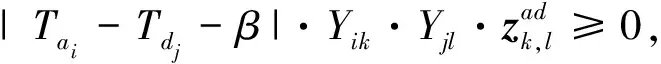
∀i,j∈F,∀k,l∈G
(10)
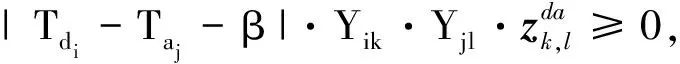
∀i,j∈F,∀k,l∈G
(11)
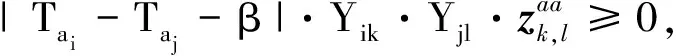
∀i,j∈F,∀k,l∈G
(12)

∀i,j∈F,∀k,l∈G
(13)
Yik∈{0,1}, 1≤i≤n, 1≤k≤m
(14)
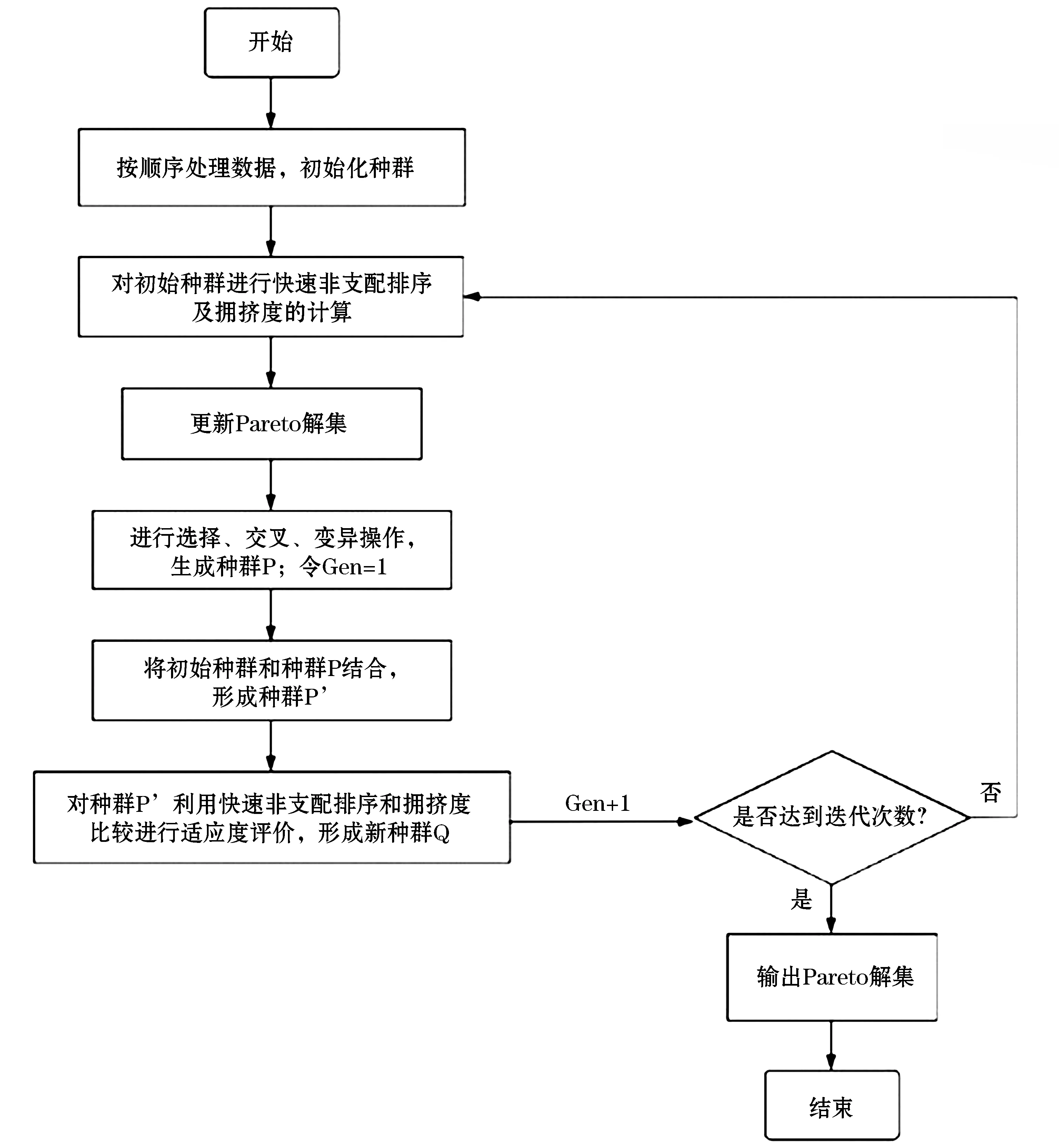
φijk∈{0,1}, 1≤i (15) 停机位分配问题是一种解空间的规模很大、会带来“组合爆炸”的组合优化问题,需要用启发式算法解决.因此,本文采用带精英策略的非支配排序遗传算法(NSGA-II)[14-15]对模型进行求解,可以加快收敛速度,提高优化结果的准确度. 1)个体编码 采用基于正整数编码的策略:个体中的每一个基因位代表一个航班,个体编码的总长度等于所有航班的数目总和加上目标函数的个数,前一段基因位上的数值代表此航班分配到的停机位序号,后一段基因位上的数值代表三个目标函数的值. 2)快速非支配排序 通过循环比较,将所有不能被任何其他的解支配的个体挑出来,赋予其非支配等级为1,然后将这些个体从种群中排除,考虑剩下的所有不能被任何其他的解支配的个体,将它们的非支配等级设为2,……对这些个体重复上述操作,直至所有个体都被赋予非支配等级. 3)适应度评价 利用种群个体的支配关系以及拥挤度的比较来评价个体的优劣,种群中所处非支配层低的个体的适应度好于所处非支配层高的个体.对于同一非支配层的个体,拥挤距离大的个体具有更优的适应度值. 4)进化操作 a)选择:根据二进制锦标赛法随机从当前种群中选择两个个体,保留非支配等级较高的个体,若二者等级相同,则保留拥挤度较大的个体,直到种群规模达到设置值. b)交叉:采用双点交叉方式,在个体编码中随机设置了两个交叉点,然后进行交换交叉点之间的部分基因. c)变异:采用均匀变异方式,分别用某一范围内均匀分布的随机数,以一个较小的概率来替换个体编码串中各个基因座上原有的基因值. 5)精英策略 将父代个体与子代个体合并后进行非支配排序,扩大了生成下一代个体时的筛选范围,达到保留优秀个体淘汰劣等个体的目的.具体的NSGA-II算法流程图如图4所示. 图4 NSGA-Ⅱ算法求解流程图 以天河机场典型日全天的航班数据为例进行验证分析,研究范围内共有可用停机位75个,其中包括远机位14个、近机位61个,航班对298个,将数据和具体运行规则的限制代入本文构建的多目标停机位协同分配优化模型中,并采用NSGA-II算法对实例进行求解.在算法中,设置种群数量为100,迭代次数6 000次,交叉概率0.8,变异概率0.05. 迭代过程中三个目标函数的变化曲线如图5所示.由于数据较大、约束较多、模型复杂度较高,在迭代将近5 800次的时候目标函数才趋于收敛.由三条曲线可知,随着迭代次数的增加,所得到的Pareto最优解对应的目标函数值逐渐减小,说明解的质量在逐代提高. 图5 目标函数的迭代变化曲线 求解结果如图6所示,图6中有一组近乎均匀的Pareto最优前沿,该前沿上有53个解,每个解都代表一种停机位分配方案,互相非支配.随着同机位航班冲突值的减少,使用远机位的航班数量和旅客步行距离在逐渐增加,这说明优化目标(1)和(2)的变化趋势是一致的,而目标(3)与(1)、(2)是矛盾的.由于目标函数是离散分布的,因此Pareto最优前沿由几个非连续的区域组成. 为验证本文建立的模型和使用的算法对停机位分配方案优化的有效性,在Pareto最优前沿中分别取优化目标(1)和目标(2)最优、目标(3)最优以及兼顾三个目标的3个方案,与人工分配的结果进行比较,如表2所示. 由表2可知,方案2的分配结果中使用远机位的航班数量为46,比方案1、方案3和方案4分别减少35.21%、16.36%和9.80%;方案2的旅客步行距离为50 542 523 m,比方案1、方案3和方案4分别减少7.54%、2.29%和1.04%.同理,方案3的分配结果中同机位航班冲突值为68.29,比方案1、方案2和方案4分别减少53.55%、43.44%和22.48%,在运行冲突方面方案3对于人工分配方案和另两个分配目标最优的方案都有很大的改进;即便是对于使用远机位的航班数量和旅客步行距离这两个优化目标,方案3的结果也比方案1分别减少了22.54%和5.37%.而同时兼顾三个优化目标的方案4的分配结果相比于方案1,也有较大的提升.可见经过NSGA-II算法优化的结果总体远远好于人工指派的结果. 在对多目标问题进行协同决策时,往往很难存在一个调度方案使得多个目标同时最优,所以在现实中决策者需要根据实际情况选择具体的调度方案.本文采用的方法对于机场工作人员有针对性地根据不同的侧重点选择符合机场实际运行情况的停机位分配方案提供了科学合理的依据.图7给出了同机位航班冲突值最小时的停机位分配方案,可以看出,在加入区域机位组合安全受限约束后,得到的停机位分配方案满足机场的实际运行规则. 图7 停机位分配甘特图 针对我国大型枢纽机场广泛使用的包含多个港湾U型区的停机坪构型,将武汉天河国际机场作为典型实例,对U型机坪进离港航空器的运行方案进行重点分析,以最小化停靠在远机位的航班数量、最小化旅客步行距离以及最小化同机位航班冲突值作为目标函数,综合考虑复杂机坪的运行模式、航班对应运营区域的限制等符合实际情况的约束,建立一体化多目标停机位分配协同优化模型.本文采用NSGA-II算法求解模型,以NSGA-II算法为框架,将所有航班所分配的停机位集合设计为染色体,进行快速非支配排序、适应度评价、进化操作等.以天河机场为实际背景,将典型日航班数据代入模型和算法进行求解.对结果的分析表明,所建立的多目标模型能够协同机场、旅客和航司三方的利益,兼顾机坪运行效率与安全,满足实际约束.采用的算法能够有效求解模型,得到相对均匀的Pareto 前沿,对于机场相关工作人员如何根据不同现实需要选择平衡各目标的停机位分配方案提供了极大的帮助.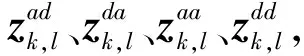
3 基于NSGA-II算法的多目标停机位协同分配仿真验证
3.1 算法设计
3.2 实例验证


4 结 语

