基于CNN的一种错误率可控图像分类算法
杨 林,周跃进
(安徽理工大学 数学与大数据学院, 安徽 淮南 232001)
神经网络的出现使得计算机视觉领域取得了一系列的突破,而计算机视觉的飞速发展也逐渐改善了人类的生活方式,一定程度上减轻了人的负担[1].近年来,图像分类与目标检测逐渐成为机器学习领域十分活跃的研究方向,被应用到现实生活中的各个领域,如人脸识别、车辆检测、行人跟踪等.然而,传统的神经网络预测都是点预测方法,这种预测方法不具备置信度衡量的特点,因此这类预测方法在高风险低容错率问题方面很难被广泛应用,在这类问题中置信度衡量极其重要,一旦预测错误将会承担极大风险[2],如生物医学上的多项重大疾病诊断问题[3].因此,对于分类问题构造具有置信度衡量的集合预测研究十分有必要.
一致性预测(Conformal Predictors, CP)作为近年来新提出的统计学习框架,最大的优点是允许用户自定义置信度进行预测[4],并且其预测准确率满足置信度.因此在神经网络中引入一致性预测的方法能够很好地克服上述中无法用置信度衡量预测结果的问题.CP在2005年首次被提出,并在之后不断地被完善与改进[5-6].由于CP可以建立在任何一种底层算法(如KNN、支持向量机、随机森林、朴素贝叶斯等)的基础之上,因此将CNN作为底层算法具有可行性.
为了解决CNN无置信度衡量的问题,本文提出了基于CNN的一种错误率可控分类算法,并以GoogLeNet和ResNet50两种CNN模型为例展开研究,提出的具体算法分别为ICP-GoogLeNet和ICP-ResNet50.
本文将GoogLeNet和ResNet50两种CNN模型作为特征提取器,引入ICP结合两种CNN模型的softmax层输出,并对新模型样本奇异值函数提出了一种新的计算方式;将ICP的可靠性的优点融入到网络中,用户可根据不同需求在线设置不同的置信度获得不同的预测结果,使得预测结果错误率可控,该方法在高风险低容错率的分类问题上具有十分重要的参考意义.
1 深度学习方法
1.1 深度学习和卷积神经网络
机器学习是人工智能的核心,是使计算机具有智能的根本途径,而深度学习作为机器学习发展人工智能的一个新兴领域,也是当今最流行的研究趋势之一[7].深度学习的概念最早是在2006年多伦多大学教授Hinton等提出,而卷积神经网络是一种学习效率非常高的深度学习模型.1998年由Le Chun提出的LeNet[8]为CNN的开山之作,但受限于当时的硬件设备受限,无法搭建更深层的网络.直到2012年Hinton的学生Alex提出的网络AlexNet[9]获得ILSVRC-12竞赛的冠军,相比于传统机器学习分类算法极大提升了分类准确率,展现出了CNN的强大优势.此后,CNN引起界内研究者的广泛研究并发展非常迅速,逐渐有准确率更高、训练更高效的模型产生,如2014年由牛津大学著名研究组Visual Geometry Group提出的VGGNet[10]、2014年由Google团队提出的GoogLeNet[11]、2015年由微软实验室提出的深度残差网络(Deep Residual Network, ResNet)[12]等.
CNN中GoogLeNet和ResNet的诸多优良性能,使其几乎成为近几年CNN中应用最为广泛的特征提取网络.而ResNet根据卷积层结构的层数不同可细分为ResNet18、ResNet50、ResNet101等,其中ResNet50分类效果较为显著,因此本文就GoogLeNet和ResNet50两种深层网络展开研究.
1.2 GoogLeNet网络模型
GoogLeNet是ILSVRC-14竞赛的冠军,该网络模型结构带参数的层数一共为22层.以往的CNN模型AlexNet和VGGNet为了学习更深层次的特征直接增加网络的深度与宽度,但这会使得模型产生巨量参数影响学习效率,并且过深的网络模型容易造成过拟合现象导致泛化能力下降.然而,GoogLeNet通过引入一种新型的Inception结构解决了上述问题,Inception结构如图1所示.
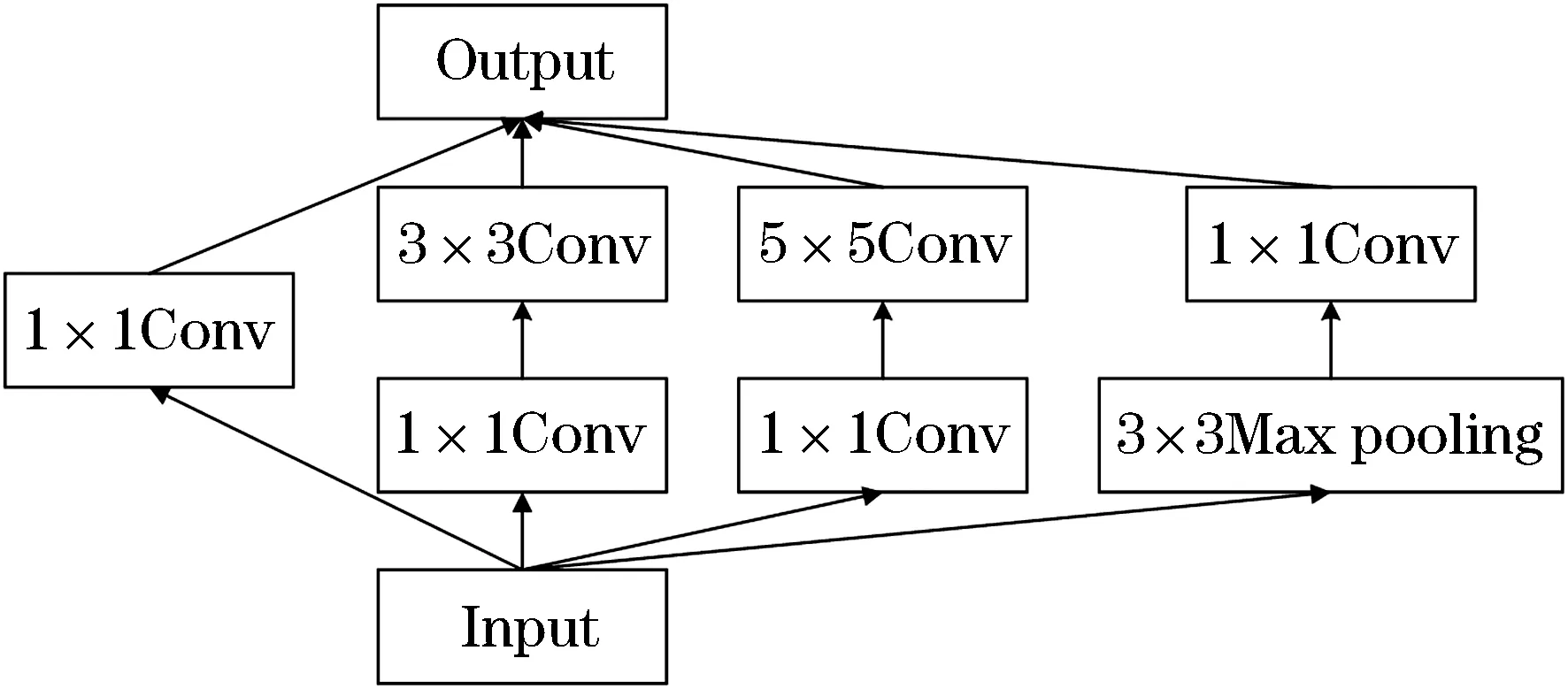
图1 Inception结构Figure 1 Inception structure
一方面,Inception结构通过1×1,3×3,5×5三种不同尺度大小的卷积核融合了不同尺寸的感受野,再经过堆叠后作为Inception结构的输出,因此该结构保留了不同尺度的信息特征.另一方面,该结构使用1×1卷积核起到了降维以及映射处理的作用,大大减少了模型参数,加快了训练效率.以32×32×512的特征图为例,用64个5×5的卷积核进行卷积,那么一共需要5×5×512×64约820 k个参数,如果在卷积之前先使用32个1×1卷积核,那么一共仅需要1×1×512×32+5×5×32×64约67 k个参数,显然使用1×1卷积核大幅减少了模型参数.
1.3 ResNet网络模型
ResNet是ILSVRC-15竞赛的冠军,斩获当年分类任务、目标检测任务第一名,是卷积神经网络发展上的一座里程碑.传统卷积神经网络模型在逐步加深网络深度后会产生梯度消失或梯度爆炸问题,通过数据初始化或正则化(batch normalization)等方法可以解决[13],但是随之而来的是模型的退化(degradation)问题,即网络层级的加深到一定程度后效果不增反降.ResNet不同于以往的网络结构,其深度甚至可以超过1 000层,该网络通过设计Residual残差块克服了模型退化问题[14],使得该网络可以通过不断加深网络层级学习更深层的特征表现更优异的效果,以ResNet50残差块为例如图2所示.其中shortcut连接采用大小为1×1的卷积核进行降维操作,相当于执行的是恒等映射,将模型退化为一个浅层网络.假设输入x通道数为256,卷积层输出为F(x),那么该结构输出为H(x)=F(x)+x,其中卷积一层通过减少通道数并用1×1卷积核起降维作用,卷积三层通道数设置与输入时x相同为256.
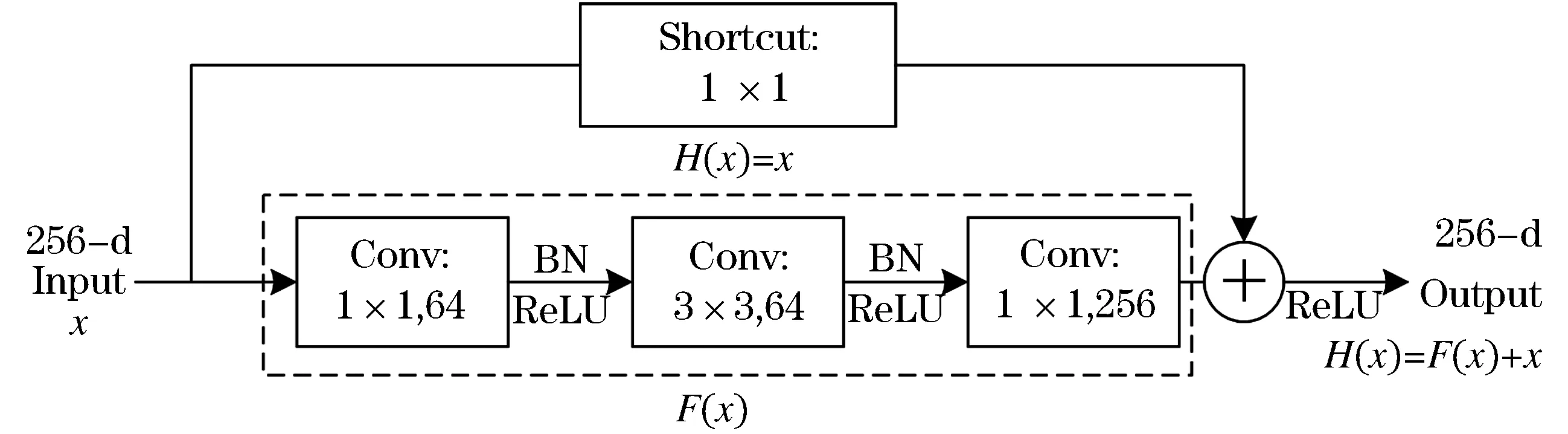
图2 ResNet50残差块Figure 2 ResNet50 residual block
2 归纳一致性预测器
本节介绍一致性预测器(Conformal Predictors, CP)的改进,即归纳一致性预测器(Inductive Conformal Predictors, ICP),以及基于CNN的ICP.ICP是由Vovk等人提出的一种基于Kolmogorov算法随机性理论的转导推论域预测机器学习算法.该算法在预测之前可以自定义置信度,再对训练样本和测试样本进行随机性检验,输出所有满足自定义置信度的随机性检验值对应的标签.因为ICP具有允许用户自定义置信度输出具有高可信度预测结果的优点,这种预测方法被广泛应用到生物医学[15-17]、时间序列[18]、图像处理等领域.
2.1 ICP基本框架
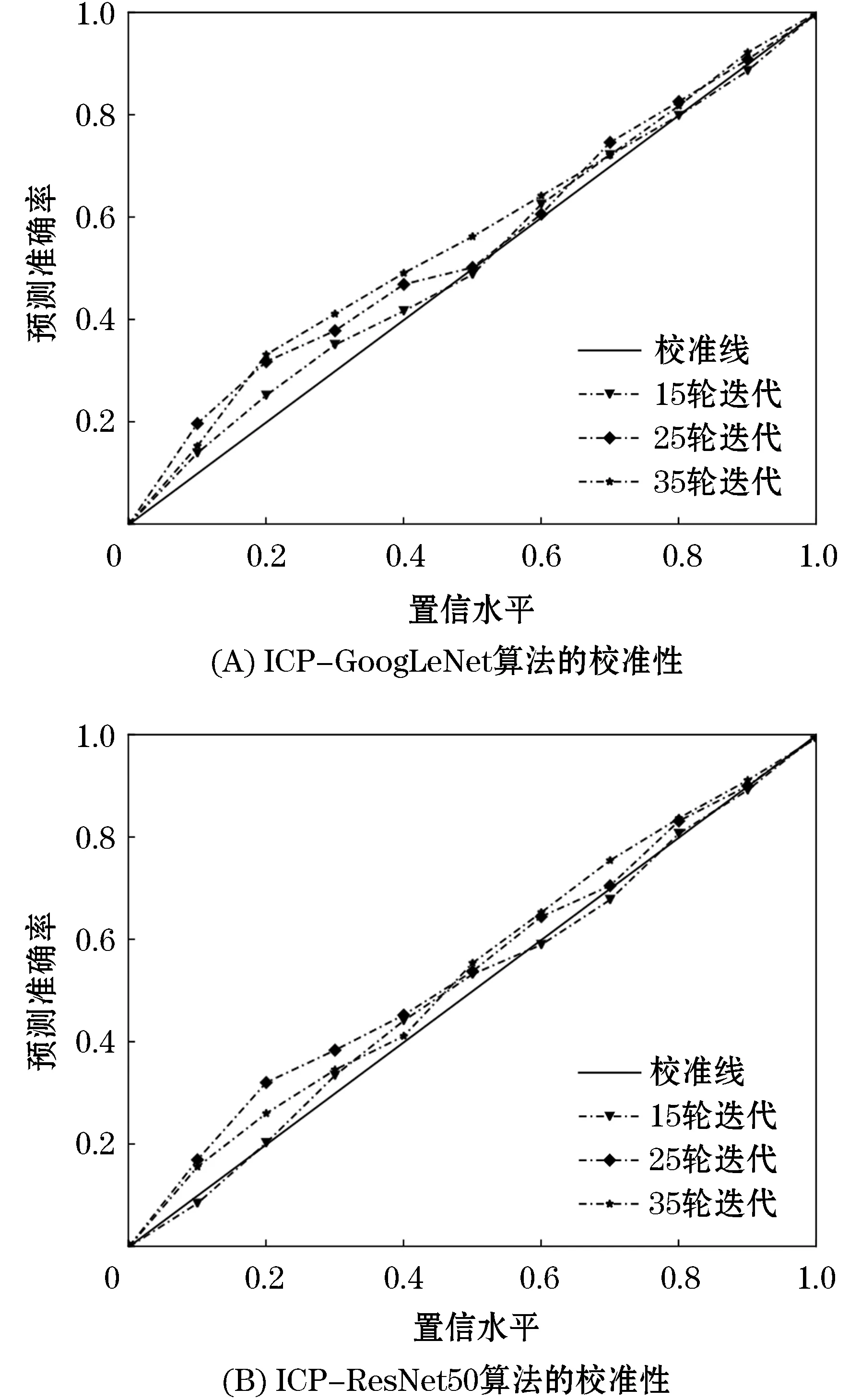
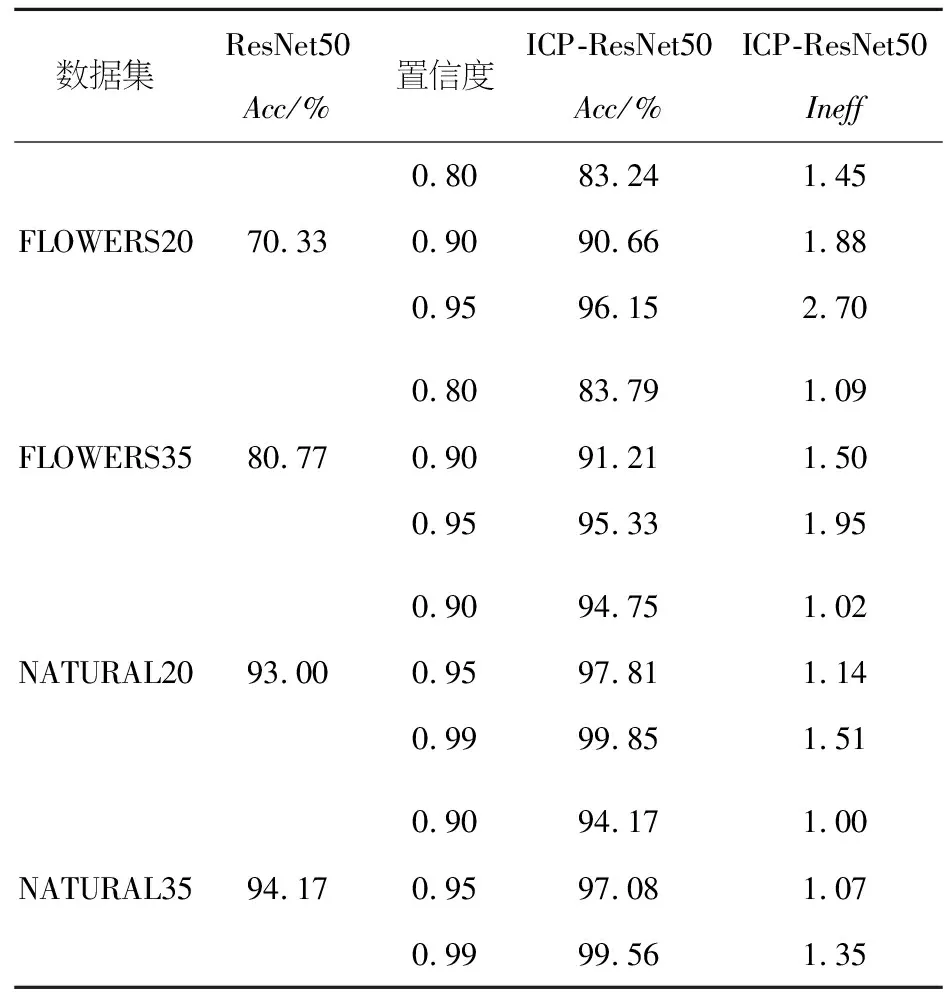
假设样本序列Z={z1,…,zn}={(x1,y1),…,(xn,yn)}∈(X,Y)n,将该样本序列分为训练集Ztra={z1,…,zk}、校验集Zcal={zk+1,…,zl}和测试集ztest={zl+1,…,zn},其中:k,l,n∈N,1 为检验测试样本的p值,考虑设计一种度量函数来衡量样本zi=(xi,yi)与训练样本Ztra之间的差异程度,即样本奇异值度量函数: αi=A(Ztra,zi),i=k+1,…,n (1) 其中:A(Ztra,zi)是一个度量样本zi和训练集Ztra之间差异大小的函数,对于不同的分类器,该函数的定义也各不相同.因此,样本zi的奇异值αi的大小能够反映该样本与yi类的不一致性程度,αi越大,表明样本zi与yi类的不一致性程度就越大,即认为zi是yi类的可信度就越小. 对于测试集中的样本zt=(xt,yt),t=l+1,…,n,在预测问题中yt需要预测,而ICP的目的是输出一个标签组成的集合Γε(zt),使得xt的真实标签yt属于Γε(zt)的概率大于1-ε,其中ε为置信度.假设测试集Ztest中xt的标签yt=yu,则zt=(xt,yu)的奇异值函数为: (2) (3) (4) ICP的奇异值度量函数是根据其底层算法所构造的,该底层算法可以是机器学习分类算法中的任何一类,如KNN、支持向量机、随机森林、朴素贝叶斯等.本节考虑基于GoogLeNet与ResNet50的ICP,分别记为ICP-GoogLeNet和ICP-ResNet50算法. 本文GoogLeNet与ResNet50两种CNN模型均使用softmax分类器进行分类,它连接着网络中全连接层的最后一层,softmax分类器输出的是每一种类别对应的概率,且所有类概率和为1.在C类分类任务中,类标签空间为Y={y(1),…,y(C)},那么对于特定的输入xi,网络全连接层输出为zi作为softmax层输入,则softmax输出结果为: (5) 网络的softmax层由C个神经元组成,每个神经元分别代表一种类别.则样本xi的奇异值度量函数为: (6) 根据奇异度量函数计算校验集Zcal和测试集Ztest样本奇异值,再将其代入式(3)求p值并输出结果.整个基于CNN的ICP算法流程如算法1所示. 算法1 基于CNN的ICP算法 输入:训练集Ztra={z1,…,zl},测试集Ztest={zl+1,…,zn},类标签空间Y={y(1),…,y(C)},自定义置信度ε,CNN模型(如GoogLeNet和ResNet50),softmax分类器Υ. 输出:测试集Ztest的归纳一致性预测集合Γε(zt). 1)将训练集划分一部分作为校验集Zcal={zk+1,…,zl},原训练集缩小为Ztra={z1,…,zk} 2)用训练集数据Ztra训练CNN模型 3)用分类器Υ输出校验集Zcal的si,i=k+1,…,l 4)用式(6)计算Zcal的奇异值αi,i=k+1,…,l 5)for :zt∈Ztest,t=l+1,…,n: 6) for:yu∈Y,u=1,2,…,C: 7) 用网络测试样本zt,并用分类器Υ输出st 10) 用式(4)计算zt的归纳一致性预测集合Γε(zt). 基于CNN的ICP算法(如ICP-GoogLeNet和ICP-ResNet50算法)的时间复杂度与CNN基层网络密切相关,现以乘法和加法为基本运算,分析本文算法在训练和测试阶段的时间复杂度. 记CNN基层网络为U,本文算法为ICP-U,设数据集中训练集大小为n1,测试集大小为n3,U在训练和测试时,所需时间分别为Utra(n1)和Utest(n3),则U的时间复杂度为: ΘU=Θ(Utra(n1)+utest(n3)) 在本文算法中,由于ICP将训练集中部分额外划分出一个校验集,设其大小为n2,则训练集大小缩减为n1-n2,故本文算法的时间复杂度为: ΘICP-U=Θ(Utra(n1-n2)+Uapple(n2+n3)+Utest(n3)) 从ΘICP-U的组成可以看出,在训练模型阶段由于Utra(n1-n2) ΘU-ΘICP-U=Θ(Utra(n2)-Uapple(n2+n3)) 由于训练模型的时间远远大于计算样本奇异值的时间即Utra(n2)>Uapple(n2+n3),因此本文算法的时间复杂度比底层算法更小. 以上研究分析表明,本文算法在减少时间复杂度的同时,能够将CNN的预测结果扩展为预测集合.该方法有助于CNN的预测性能得到提升,并使其预测结果具有可靠性. 本节将通过数值实验来验证本文算法的性能.实验共分为两个部分,第一部分检验本文算法准确率的校准性,第二部分研究在迭代不同次数以及不同置信度下本文算法的性能评估指标变化情况,并以GoogLeNet和ResNet50作为CNN基层网络进行实验. 实验数据集采用的是kaggle官网的FLOWERS、NATURAL数据集.两个数据集图像大小均不一致,模式为RGB三通道,其中:FLOWERS数据集分为雏菊、玫瑰、蒲公英、向日葵、郁金香一共5个类别,训练图片3 306张,测试图片364张.NATURAL数据集分为现实生活中的飞机、汽车、猫、狗、花、水果、摩托车和人8个类别,共6 899张图像.本文算法需要额外的校验集,因此在使用本文算法训练模型时,需要从训练集划分部分数据作为校验集.划分后的FLOWERS数据集的训练集图片3 000张,校验集图片306张,测试集图片364张.划分后的NATURAL数据集的训练集图片5 513张,校验集图片700张,测试集图片686张. 数据预处理:随机水平翻转训练集和校验集图像,将FLOWERS数据集所有图像随机裁剪或调整使其统一大小为(224,224)的图像,并进行标准化(Normalize)处理,随机打乱数据使其满足独立同分布.批训练和测试样本大小(batch_size)设为32,网络使用交叉熵损失函数: 其中:N为训练样本总数;C为类别数;ync为符号函数,当第n个样本的真实标签为c时ync取1,否则取0;pnc为第n个样本预测标签为c时的概率.优化阶段使用自适应矩阵估计(adaptive moment estimation, Adam)优化器优化模型,学习率初始值设为0.000 2. 衡量归纳一致性预测算法性能的指标主要有两个,分别是预测准确率和平均预测集合长度.预测准确率定义为: 其中:ε为自定义置信度,|{*}|表示集合{*}的大小,即集合内元素的个数,若Acc≥ε则算法有效.在域预测中,平均预测集合长度越小表示预测精确度越高,此时的预测集也更为高效.而平均预测集合长度定义为: 其中:f(w)一般使用恒等函数f(w)=w,|Γε(xi)|表示预测集Γε(xi)即所含的元素个数.因为ICP的输出总共可以分为三种情况,分别是空集、包含一个元素的单点集和包含多个元素的集合,所以Ineff该指标越小则表示从整体看预测集合越小,预测精确度越高. 这两种指标是一个权衡问题,准确率的提高会导致精确度的减小,因此需要根据用户的实际需求调整置信度权衡二者的大小. ICP-GoogLeNet与ICP-ResNet50的优点是不仅融入了基层网络的优良预测性能,而且还能够对结果提供具有置信度的预测.本节检验预测准确率的校准性,展示在不同置信度下它们的变化.针对NATURAL数据集,分别记录训练数据第15、25、35次迭代预测准确率,图3表示ICP-GoogLeNet和ICP-ResNet50算法预测准确率与置信度的关系(反映算法的校准性),两种神经网络均使用随机初始权重进行训练. 图3 算法的校准性Figure 3 Calibration of the algorithm 在图3中,校准线表示本文算法预测准确率Acc与置信水平ε完全相等的情况即Acc=ε,而本文ICP-GoogLeNet和ICP-ResNet50算法在任何置信度下,始终有Acc≥ε,表明其准确率始终高于置信度,故本文算法满足校准性.在满足校准性的基础上,算法的准确率十分贴近且略高于校准线,表明提出的算法能够精准控制预测准确率.无论网络进行多少轮次迭代,置信度依然能够非常精准地控制准确率,表明本文算法的校准性与迭代次数无相关性. 为了说明本文算法的有效性,以传统的GoogLeNet和ResNet50算法为基准,在表1、2中分别记录在不同置信度和不同迭代次数下本文算法的预测准确率和平均预测集合长度.其中:数据集FLOWERS20和FLOWERS35分别表示对FLOWERS数据集循环迭代的第20次和35次结果,NATURAL数据集同理. 表1 ICP-GoogLeNet的预测性能 表2 ICP-ResNet50的预测性能 从表1、2中可以看出: 1)在预测准确率Acc方面,随着置信度的增大,预测准确率也随之增大,并且置信度能够十分精准得控制着预测准确率,始终满足Acc≥ε.当置信度取较高值如0.90、0.95、0.99时,本文ICP-GoogLeNet和ICP-ResNet50算法的预测准确率高于传统GoogLeNet和ResNet50算法; 2)在平均预测集合长度Ineff方面,随着置信度的增大,平均预测集合长度也随之增大.FLOWERS和NATURAL数据集平均预测集合总长度分别属于区间[0,5]和[0,8],传统算法为点预测结果,故其长度均为1.00,而本文算法的平均预测集合长度十分接近于1.00,表明算法的预测精确度非常高; 3)在ICP-GoogLeNet和ICP-ResNet50二者算法之间,后者的预测效果更好,相同条件下在FLOWERS和NATURAL数据集上,后者较前者不仅预测准确率更高,而且平均预测集合长度更小,即从两个指标中看ICP-ResNet50都能够达到更好的效果. 文本算法融入了归纳一致性预测的优点,能够输出具置信度的集合预测结果.为了突出算法的置信度控制错误率的稳定情况,现使用3.4节中同等参数设置训练网络模型.将ICP-GoogLeNet算法的置信度设置为0.99在图中记作ICP-GoogLeNet 0.99,图4、5分别展示了ICP-GoogLeNet和ICP-ResNet50算法在NATURAL数据集上不同置信度条件下的预测准确率、平均预测集合长度与迭代次数之间的变化曲线. 图4 算法的预测准确率Figure 4 The prediction accuracy of the algorithm 图5 算法的平均预测集合长度Figure 5 Mean inefficiency of the algorithm 从图4、5中可以看出: 1) ICP-GoogLeNet和ICP-ResNet50算法能够十分精准地控制预测准确率,检验了算法的有效性,并且这与基层算法的预测性能无关.如图4中的GoogLeNet与ResNet50基层算法预测准确率相差甚远,但是并不影响其校准性,而且校准性不随迭代次数的变化而变化; 2) ICP-GoogLeNet和ICP-ResNet50算法的平均预测集合长度会随着网络的加深而逐渐减小,这有利于提升算法性能,根据实际需求,允许用户训练更深层次的网络得到更精确的预测集合; 3) ICP-ResNet50算法比ICP-GoogLeNet算法具有更好的预测效果,主要表现在如下两个方面:1)从平均预测区间长度可知,ICP-ResNet50算法不仅下降速度更快,而且长度更小即预测精确度更高;2)从预测准确率和平均预测集合长度变化曲线的波动情况可知,ICP-ResNet50算法的泛化能力更强,能够更精准地学习到图像的内部特征. 针对卷积神经网络预测结果错误率不可控且预测结果可靠性低的问题,本文将归纳一致性预测与GoogLeNet和ResNet50结合,提出了ICP-GoogLeNet和ICP-ResNet50预测算法.通过算法的复杂度分析可知,提出的算法拥有更快的训练速度和学习速度.实验结果表明,提出的算法继承了归纳一致性预测的可靠性优点,即置信度控制预测准确率输出的结果,并且预测结果的精确率也非常高.以上分析和研究表明,本文算法的预测结果具备置信度衡量的特征,并且预测精确率也能得到较好的控制,其建模和研究对高风险容错率低的分类问题具有非常重要的参考意义,如医学诊断、电网调度等领域具有较高的参考价值.

2.2 ICP-GoogLeNet与ICP- ResNet50算法

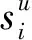

2.3 时间复杂度分析

3 实验结果与分析
3.1 实验数据集与参数设置
3.2 性能评估指标
3.3 算法的校准性
3.4 算法的预测性能

3.5 不同置信度下的预测效果比较


4 结 语

