基于改进自抗扰的永磁同步电机控制系统

黄茂源， 吴 一， 王 磊， 代文昭

（西安航天精密机电研究所， 陕西 西安 710100）

0 引言

永磁同步电机（Permanent Magnet Synchronous Motor，PMSM）具有功率密度高、体积小、转矩电流比高、结构简单等特点，并且伴随着电力电子技术、稀土永磁材料等技术的发展， 永磁同步电机控制系统得到了人们越来越多的注视，并被广泛的使用到机器人、数控机床、航空航天等领域[1]。 由于其非线性强耦合的特性，传统的PID 控制器无法在控制精度和扰动抵抗等方面达到预期的要求[2]。近年来，滑模控制、自适应控制、滑膜变结构控制等非线性控制策略被提出并应用于永磁同步电机控制[3]。 但这些非线性控制存在对模型精度要求比较高。 自抗扰控制算法是由韩京清院士基于传统PID 固有缺陷改进提出的一种控制方法[4]，其设计不需要依赖精确的数学模型，核心思想是把系统未建模的内部扰动和未知外部扰动归结为 “总扰动”来进行观察额补偿[5]。

自抗扰控制器主要包括三个部分：跟踪微分器（tracking differentiator）、扩展状态观测器（extended state observ er）和非线性状态误差反馈控制（non-linear state error feedback）[6]。 各部分需要整定的参数随着阶数的增加而增加，影响其在实际应用中的实时性，从而影响控制性能[7]。

本文选择在电机三环控制中的速度环中采用一阶自抗扰控制器。 并基于永磁同步电机旋转坐标系下数学模型，采用空间矢量脉宽调制技术（SVPWM）对目标电压进行调制，并利用在Matlab/Simulink 环境下进行仿真实验，与原速度环的PI 控制进行分析和比较。 实验结果表明，采用ADRC 控制，永磁同步电机具有更好的稳态性能、动态性能和鲁棒性。

1 永磁同步电机数学模型

本文以表贴式永磁同步电机为例， 表贴式永磁同步电机有着d、q 轴电感相等的特点Ld=Lq，为了建立现实可行的数学模型，做如下的假设：

（1）忽略磁饱和、磁滞和涡流因素对电机的影响，假设电机磁路是线性、可叠加的。

（2）转子上没有阻尼绕组，永磁体没有阻尼作用。在此假设下，建立永磁同步电机数学模型如下：

式中：ud，uq—定子电压矢量的交直轴分量；id，iq—交直轴电流；Ld，Lq—交直轴电感，由于选用表贴式PMSM，其交直轴电感相同，取Ld=Lq=Ls。 ωm、np、J、Ψf分别为机械角速度、极对数、转动惯量和永磁体磁链，Kt、B、TL分别为转矩常数、摩擦系数和负载转矩。

为控制简单，无需考虑id、iq间耦合作用，采用id=0 控制方法，则数学模型如下：

根据自抗控制原理， 将iq作为转速的被控对象，即ADRC 的输出，将负载转矩变化、摩擦系数、直轴电流作为系统的扰动。 将式（1）变形为

观察式（3），永磁同步电机电流环是一阶模型，因此可以设计一阶的速度环ADRC 控制器。

2 自抗扰控制器设计

如图1 所示，为标准的自抗扰控制器原理结构图，其由跟踪微分器、扩展状态观测器、非线性状态误差反馈控制三部分组成。

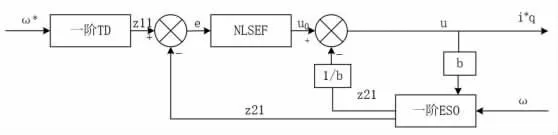
图1 自抗扰控制原理图

设一阶被控对象为：

式中：x—状态变量；u—信号输入；y—信号输出。

2.1 跟踪微分器模型

式中：y*—期望输出；z11—y*的跟踪信号；fal—非线性最速控制函数，定义为：

式中：α—非线性因子；δ—滤波因子， 最速控制函数有着大误差小增益，小误差大增益的特性。其中需要整定的参数为速度因子r，r 的取值越大跟踪速度越快，但是，r 过大会引入噪声和大的超调， 因此r 的取值应在保证速度的前提下，取尽可能小的数值。

2.2 扩展状态观测器

式 中：z12，z22分 别 为x 和 其 扰 动 值 的 观 察 信 号；β01，β02是ESO 的增益。 状态观测其中有α1、δ1、β01和β02四个参数需要整定。α1一般根据经验选取0.5。最速控制函数fal 函数线性区间宽度的选取受到系统的误差范围的影响， 取值过小会使控制系统产生高频脉动，取值过大会减弱非线性反馈的效果，一般取值在0.01 左右。 扩展状态观测器的增益取值受仿真周期影响， 取值过大则系统调节速度越快，但是取值过大将导致超调。

2.3 非线性状态误差反馈控制模型为：

式中：β1是NLSEF 的增益。 NLSEF 共有3 个参数需要整定：α2、δ1、β1， 一般α2选取0～1 之间的数，δ2选取与δ1相同，取0.01 左右。 β1一般采用试凑法进行调节。

根据设计的控制器， 可以得到基于一阶速度环的的永磁同步电机系统矢量控制模型，如图2 所示。

图2 基于ADRC 的PMSM 控制模型

3 仿真分析

为验证本文设计的一阶自抗扰永磁同步电机控制的可行性和有效性， 本文选择在Matlab/Simulink 中进行仿真，并与PI 结构进行对比。 电机参数设置如下：极对数Pn=4，定子电感Ld=8.5mH，定子电阻R=2.875Ω，磁链Ψf=0.175wb，转动惯量J=0.001kg·m2，阻尼系数B=0N·M·s。额定转速n=1000t/min。

在PI 控制系统中， 速度环参数设置为Kωp=0.14，Kωi=7；将两个电流环PI 控制器设置为相同参数，其中比例增益Kip=1.7，积分增益Kii=287.5。

在永磁同步电机自抗扰控制中， 电流环Kip=1.7，Kii=287.5。一阶非线性电流环ADRC 的参数取为：ESO 中α1=0.4，δ1=0.01，β01=300，β02=4000；NLSEF 中：α2=0.5，δ2=0.01，β1=100，b=3200。

仿真时长为0.4 时，为在给定转速n=1000r/rad，负载转矩初始时为0.1N·m，在t=0.2s 时跳变为10N·m。 电机的期望转速设置为ω·r=500r/min，仿真结果如图3 所示。

图3 转速仿真结果

从图3 中可以看出，ADRC 控制方法下，电机转速稳态精度更高。 与传统PI 控制在启动时出现一定的振荡和超调相比，ADRC 在启动时可以更快速地跟踪期望转速，并且更加平稳。 此外，在外部出现负载突变时，恢复到期望转速的速度更快。

图4 对两种策略下电磁转矩进行分析，其中PI 策略下的电磁转矩的脉动约为0.21N·m， 而ADRC 策略下的电磁转矩脉动约0.11N·m。 与PI 控制策略相比较， 自抗扰控制策略下的电磁转矩脉动更小， 且当电机启动时以及负载突变时，ADRC 转矩的输出更为平滑，具有更小的振荡。

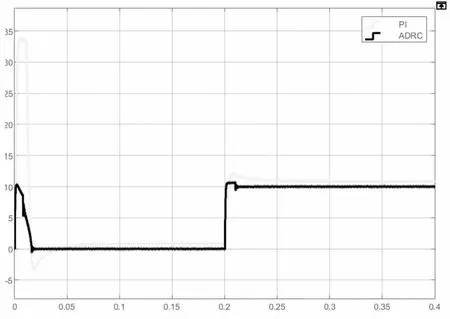
图4 加入负载后转矩变化

4 结束语

本文将PMSM 传统速度环中的PI 控制用一阶ADRC替换。 实验证明，一阶ADRC 比传统的PI 控制有着更好的动态性能和抗扰动能力。并且，简化后的自抗扰控制器具有结构更简单，待整定参数少等优点。为其他自抗扰的应用提供了相应的参考。