一种改进的梯形双频相移相位展开方法*

谢浩翔,万 程,杨 博

(安徽大学 互联网学院 智能科学与技术系,安徽 合肥 230031)

结构光三维成像技术是一种有效的光学三维测量方法,在生物医学、工业检测和逆向工程等领域有着广泛的应用[1-4]。其中,条纹投影轮廓术(Fringe projection profilometry, FPP)应用最为广泛。FPP方法使用投影仪投射一系列周期性图案至目标物体,同时使用摄像机捕捉经过物体调制后的条纹图像[5-7]。然后,从物体的几何外形引起的相位变化信息中恢复物体的三维表面信息。常用的条纹分析方法有相移法[8]和傅里叶变换法[9]。与傅里叶变换法相比,相移法具有更高的精度,同时相位分析是逐像素的,分辨率更高。相移法也因此成为FPP技术中应用和研究的热点。通过上述技术获得的包裹相位信息,其范围被截断在(-π, π)。因此,需要通过相位展开来消除2π不连续性,以获得绝对相位。目前最常用的相位展开算法包括灰度编码[10]、相位编码[11]、双频法[12]等。灰度编码法包括二值格雷码法和n级灰度编码法,这类方法受系统离焦模糊和环境随机噪声影响较大,容易引入相位展开误差。相位编码法将条纹级次信息编码到条纹的相位域,表现了较好的抗噪性和抗离焦性能,但受限于系统的非线性,其频率不能过高。相比而言,双频法利用低频相位获得较好的抗噪性能,高频相位保证了测量精度,能够很好地避免相位展开误差的出现。传统的双频利用两种不同频率的正弦条纹,低频相位作为高频相位展开的依据,完成一次测量需要6幅图像。为了提高测量的效率,Li J等[13]提出了复合双频的方法,将两种频率的条纹复合在5张图中,提高了测量效率。但相较于两组独立频率条纹的方法,复合频率方法对噪声较敏感,容易产生相位误差。

为了在提升测量效率的同时,保持双频测量方法的鲁棒性。文中提出一种改进的梯形双频相移解包裹方法。文中将传统梯形条纹中折角线替换成正弦函数曲线,使得过渡区域更加平滑。所提出的方法的测量深度范围在相域内为6π,相较于原来的方法提高了3倍。改进之后的方法,相移梯形的相移为2π,整个周期为6π。改进后的三步相移梯形条纹作为双频中的低频组,同时为高频条纹提供图像背景强度信息,所以高频条纹组只需要2幅图像。

1 基础理论

1.1 相移算法

N步相移算法因其测量速度快、测量精度高和非接触的优点[14],而被广泛地应用于相位测量中。在N步相移算法中,三步相移算法是高速三维测量应用中的最佳选择,因为它需要最少的图像来获得绝对相位图。三步相移算法的步长是2π/3,每个条纹的强度值可以表示为:

(1)

式中,A(x,y)是测量环境背景光强;B(x,y)是条纹的调制度;φ(x,y)是截断相位;(x,y)是图像坐标点。依据相移算法,A(x,y)、B(x,y)、φ(x,y)可分别通过下式计算得到(为了公式简洁,下文省略坐标(x,y):

(2)

(3)

(4)

通过求解方程(见式4)可得到截断相位,因为反正切函数的值域范围只有-π/2到π/2。2π相位跳变点需要通过相位展开算法消除。相位展开算法的核心问题是获得条纹级次k(x,y)。最终绝对相位可以由式5得到

Φ=φ+2π×k

(5)

1.2 双频相位展开方法

双频条纹算法包括一组低频条纹和一组高频条纹,为了提升测量效率,Zuo C等[15]提出3+2的双频相位展开算法。该方法中需要2幅低频条纹和3幅高频条纹图像,其强度可表示为:

(6)

式中,Il1(x,y)、Il2(x,y)为低频条纹,Ih1(x,y)、Ih2(x,y)、Ih3(x,y)为高频条纹;φl(x,y)、φh(x,y)分别为低频、高频条纹的截断相位。对于高频条纹,其截断相位φh(x,y)可由式4计算得到,而背景强度可通过下式计算:

(7)

低频条纹的截断相位可由式8计算所得:

(8)

假设φl只有一个周期,则Φl=φl。根据低频绝对相位Φl和高频绝对相位Φh的数学比例关系,可计算出φh所对应的条纹级次:

(9)

式中,fh和fl分别表示高频条纹和低频条纹的频率。最终计算出:

Φh=φh+2π×kh

(10)

传统的双频算法的原理图如图1所示。当低频周期为1时,绝对相位与截断相位相等。通过式9和式10可以得到平滑连续的绝对相位Φh。

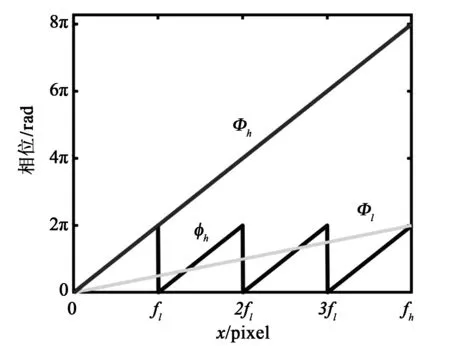
图1 传统双频相移算法原理图

2 改进的梯形双频相移解包裹方法

为了提高条纹解析的效率,P. S. Huang等[16]提出了梯形相移算法。梯形相移条纹在图像强度变化上不再是正弦曲线,而是呈梯形变化(见图2a)。梯形条纹是基于图像强度编码的,条纹处理速度较快。

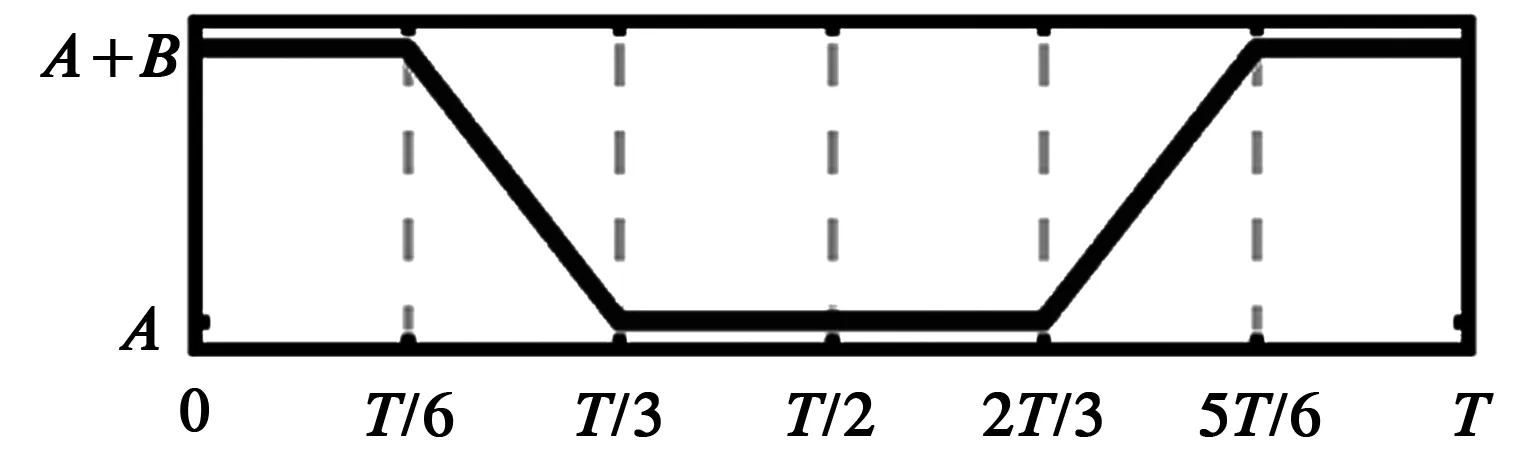
a) 传统的梯形条纹

本文提出使用正弦曲线代替梯形过渡的斜线,通过正弦编码,将其解析的值域扩展到0～6π。同样使用三步相移算法,那么改进后的梯形条纹强度可表示为:

(11)

(12)

(13)

三步相移梯形条纹强度分布如图2b～图2d所示。根据上述图像强度在局部区域的不同获取局部编码顺序M来获取梯形条纹的相位分布。

(14)

通过上述3个方程获取初步相位图:

(15)

式中,Tmax(x,y)、Tmed(x,y)、Tmin(x,y)分别表示点在3幅图像中强度的最大值、中间值和最小值。r(x,y)的分布如图2e所示,其值域范围为(0,π]。结合式14所获取的局部顺序信息,可获取最终的相位展开图R(x,y)(见图2f)。显然,改进后的梯形条纹相位图具有[0,6π)的值域范围。改进后的梯形条纹替换传统双频条纹中的低频正弦条纹,假设两组条纹频率与传统双频两组条纹频率相同,那么条纹级次的可由下式计算获得:

(16)

通过获取的条纹图像,计算得到条纹级次,将级次信息与截断相位代入到式5,可获取最终的绝对相位信息。

本文提出的双频方法,略微不同于1.2中的双频相位展开方法。本文将改进的梯形条纹作为低频部分,高频部分采用2幅正弦条纹。改进的梯形条纹,在过渡部分更加平滑,在一定程度上提高了低频部分的鲁棒性能。本文方法的基本框架图如图3所示。

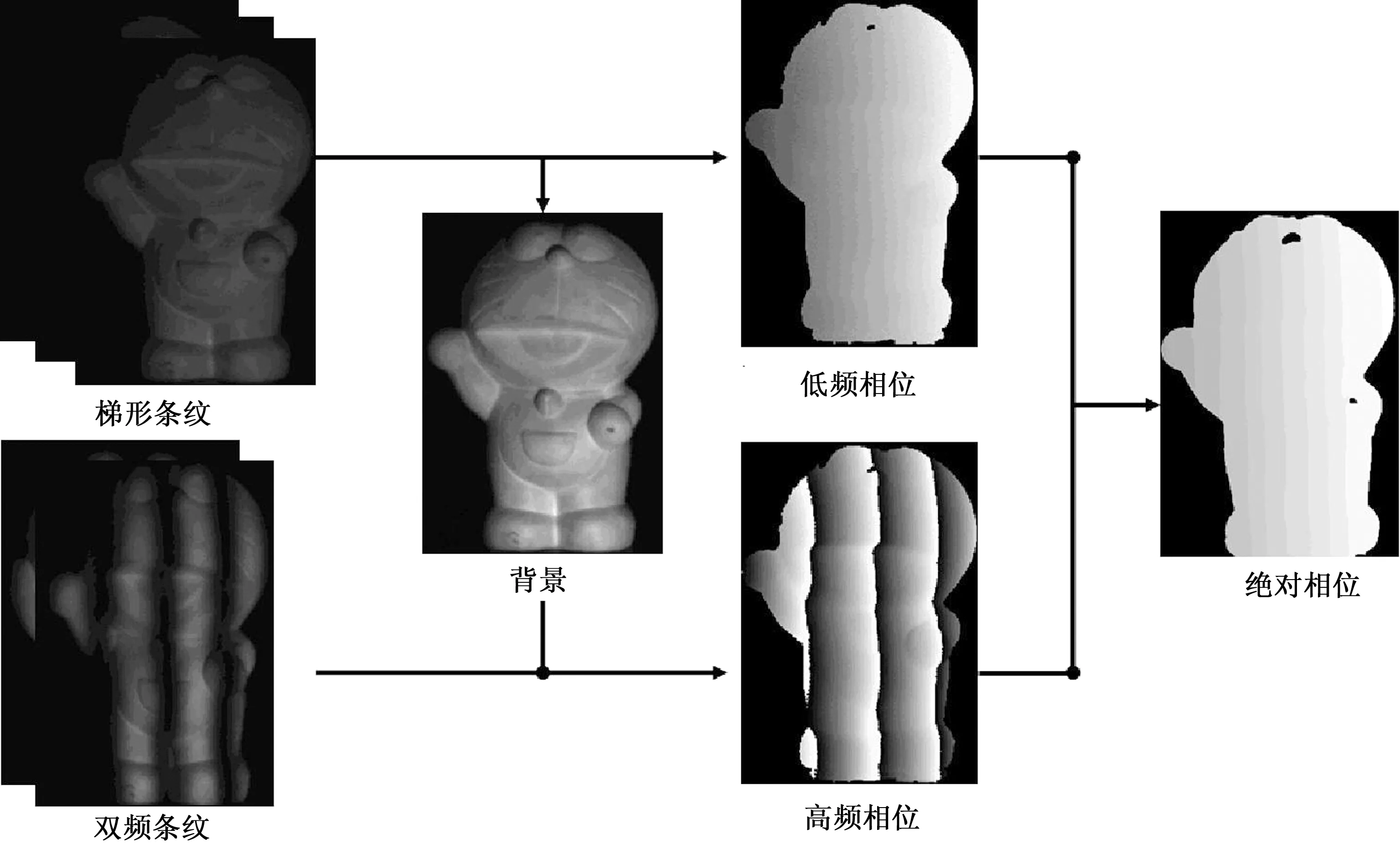
图3 改进梯形双频法的基本框架图

3 实验结果与分析

3.1 仿真实验与分析

为了验证该方法的有效性,进行了仿真实验。仿真图像的分辨率为800 pixel×800 pixel,改进梯形条纹频率为1,高频条纹频率为16。仿真图像加入信噪比(SNR)为30的噪声,然后对双频条纹进行处理。图4所示为加入噪声之后的本文方法仿真的结果。从图4可以看出,即使条纹图像的噪声很大,本文方法仍能够恢复较为平滑的仿真平面。但是由于图像强度在边界部分更容易受噪声干扰,会出现些许噪点。实际运用中可以使用半周期算法校正[17],也可以缩小测量的范围,将测量区域集中在图像中央。

a) 改进梯形低频条纹

3.2 物体测量实验与分析

为了验证本文方法在实际测量中的有效性,搭建了条纹投影系统。该系统包括DLP Light-Crafter 4500 和摄像机Point Grey Chameleon3,其中投影仪的分辨率为912 pixel×1 140 pixel,摄像机的分辨率为1 280 pixel×1 024 pixel。实验过程中,梯形条纹的频率为1,高频条纹频率为16。

实验中首先测量单个雕塑模型,其测量结果如图5所示。测量结果表明了该方法在测量单个物体时具有很好的性能。为了进一步验证该方法在测量不连续的两个独立物体时的准确性,实验测量了两个相互独立的雕塑模型。投影仪将本文设计生成的条纹投射至物体表面,摄像机同步采集被物体调制后的变形条纹图像。摄像机采集的图像如图5所示,其中图5a～图5c为低频改进的梯形条纹调制图,图5d～图5e为高频正弦条纹调制图。

a) 低频相位为0的梯形条纹

将采集到的图像使用本文方法进行处理,处理结果如图6所示。其中,图6a为改进的梯形条纹求得的低频相位,从图中可以看出,图像边缘部分有轻微的噪声;图6b～图6c分别为通过高频截断相位和双频算法获得的条纹级次;使用式10可获得最终的绝对相位,从图6d可以看出,噪声信息得到了抑制。图7b所示为最终三维重建出的物体表面,重建的物体表面光滑,几乎无误差,表面形貌接近图7a所示的实际物体,进一步表明了本文方法的有效性。

a) 改进梯形低频相位

a) 物体实物图

4 结语

本文提出了一种改进的梯形双频相移相位展开方法。用正弦曲线代替梯形折角线,使过渡区域平滑。改进的梯形相移条纹其测量深度范围为(0,6π],相较于传统的正弦条纹扩大了3倍,并在6π相位域中获得了更好的抗噪声能力。仿真和实验结果验证了该方法的有效性。