城市道路交叉口行人专用相位适用性研究

安喜才， 曹 义， 袁 超， 刘 威， 韩宜森

（1 郑州科技学院车辆与交通工程学院， 郑州 450064； 2 林同棪国际工程咨询（中国）有限公司， 南京 211106；3 中国南方航空股份有限公司， 上海 310000）

0 引 言

城市道路交叉口是人车冲突常发地，传统上以优化车辆交通为主的信号控制方案常常使行人交通处于被动状态，行人过街安全备受挑战。 为了改善行人交通过街环境，研究学者提出在交叉口设置行人专用相位以保护行人过街安全，即为行人交通提供一个单独的信号控制相位，在此相位区间允许行人在交叉口空间上直行或斜穿过街，车辆禁止通行。

早在上世纪，关于行人专用相位，国内外学者就进行了相关研究，主要从行人专用相位设置的安全、效率以及条进行分析和评价。 在安全方面，Abrams等学者［1］研究发现，当行人专用相位时间过长时会带来较多违章过街人数，易导致严重交通事故发生。Ivan 等学者［2］发现有行人专用相位的交叉口比传统两相位信号控制交叉口存在较多的行人违章过街现象。 Jensen［3］的研究表明行人专用相位的设置可使人车冲突的发生率减少7%～63%。 Zhang 等学者［4］分别对有、无行人专用相位交叉口人车冲突进行了分析，结果表明行人专用相位发生的人车冲突数较少，但严重程度较高。 袁黎等学者［5］通过建立的有行人专用相位的交叉口安全效益综合评价方法得出当人流或转弯车辆较多时应采用行人专用相位。 在效率方面，Bechtel 等学者［6］对不同地区有行人专用相位的交叉口进行了研究，发现行人专用相位减少了行人13%的过街距离，但未提高通行效率。 翟京等学者［7］利用Synchro Studio 软件对饱和状态下交叉口有、无行人专用相位两种情况进行了仿真对比，发现行人专用相位设置大大增加交叉口车辆交通的延误。 钱大琳等学者［8］对以往行人专用相位控制模式进行调整，提出以人均、车均延误为目标建立信号配时优化模型，验证了新方案的有效性。 Medina等学者［9］对有行人专用相位的交叉口行人过街方式进行了研究，结果显示在行人黄灯期间，对角穿行人数远少于平行过街。 王嘉文等学者［10］构建有无行人专用相位的交叉口车辆乘客延误以及行人过街延误模型，并以两者的总延误为判断指标，讨论行人专用相位适用条件。 在设置条件方面，Ma 等学者［11］对比了行人专用相位与常规两相位两种信号控制模式，发现车辆转弯率或行人对角穿行率大于0.6 时，行人专用相位更具优势。 Ma 等学者［12］以交叉口人车暴露数和行人违章率作为安全评估指标，以人车延误作为效率评估指标，建立行人专用相位与常规两相位信号控制定量选择标准。 冯洁等学者［13］同时考虑行人和车辆效益，构建了行人专用相位信号控制策略的适用性评价模型。 王雪元等学者［14］分别以交通事故数和交通延误作为交叉口安全和效率的评价指标，建立了有（无）行人专用相位控制的交叉口运行成本优化模型，确定了行人专用相位设置阈值。 董洁霜等学者［15］从交叉口人车过街公平性的角度出发，在分析人车冲突机理的基础上，建立了交叉口行人专用相位动态设置模型。

综上，行人专用相位消除了交叉口时空上的人车冲突，但同时大大增加车辆交通延误时间，降低交叉口通行效率。 另外，多数研究以安全或延误单方面指标判断行人专用相位设置条件，未基于交叉口人车交通特性，从行人安全和交叉口运行效率、整体效益对行人专用相位进行优化，模型缺少一定的适用性。 鉴于此，本文以两相位交叉口为研究对象，在分析人车冲突机理的基础上，推导出人车冲突数估计模型和人车冲突延误模型，以人车期望冲突数为安全指标，以人车冲突延误和信号延误作为交叉口效率指标，构建交叉口有（无）行人专用相位适用性模型，使得在提升行人过街安全的同时保障交叉口以最高效率运行。

1 人车冲突机理

在常规两相位信号控制交叉口，由于信号方案的设置，行人交通过街可分为集中过街阶段和随机过街阶段［16］。 行人集中过街阶段如图1 所示。 在行人集中过街阶段，行人交通是以人群的方式通过交叉口，转弯车辆需等待人群通过人车冲突点后驶出交叉口。 此阶段延误包含信号延误和受人群过街影响产生的车辆冲突延误。 人车冲突数则定义为转弯车辆到达人行横道上人车冲突点等待通过冲突点的行人数量。

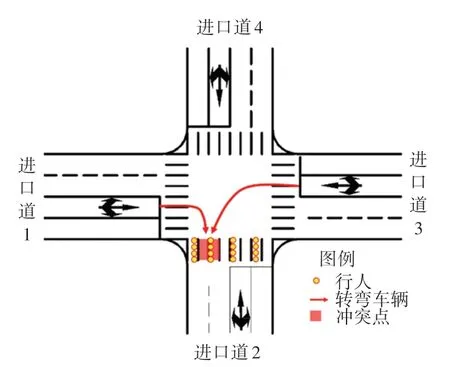
图1 行人集中过街阶段Fig. 1 Pedestrian concentration crossing stage

行人随机过街阶段如图2 所示。 在行人随机过街过程中，行人和车辆到达冲突点均为随机达到，人车冲突和延误的产生受双方达到规律的制约。 此阶段延误包括信号延误、受行人到达影响产生的车辆冲突延误和受转弯车辆到达影响产生的行人冲突延误。 人车冲突数定义为车辆和行人同时到达冲突点的次数。 此外，本文针对非饱和两相位交叉口进行研究，故假设行人和车辆到达均服从泊松分布。

图2 行人随机过街阶段Fig. 2 Pedestrian random crossing stage

行人专用相位如图3 所示。 对于有行人专用相位交叉口，由于行人专用相位的设置，行人和车辆在时空上进行了隔离，消除之间的冲突。 行人和车辆交通过街效率受信号配时方案的影响。

图3 行人专用相位Fig.3 Pedestrian dedicated phase

通过上述人车冲突发生机理分析，以支持行人专用相位适用性模型中人车期望冲突数和冲突延误计算公式的推导。

2 安全模型构建

2.1 行人专用相位设置前交叉口人车冲突数估计模型

根据人车冲突推导行人集中过街阶段和行人随机过街阶段人车期望冲突数估计模型。

（1）行人集中过街阶段人车期望冲突数。 此阶段人群在人车冲突点消散时间：

其中，j为人行横道编号，j＝1，2，3，4；C为信号周期，单位为s；为第k相位行人绿灯时间，单位为s；dj为第j人行横道远端行人到达冲突点距离，单位为m；vp为行人过街速度，单位为m/s；为第j人行横道两端行人到达率，单位为ped/s；；bp为每排过街行人时距，单位为s；r为每排行人横向距离，单位为m；wpj为第j人行横道宽度，单位为m。

转弯车辆到达人车冲突的时间：

其中，i为进口车道编号，i＝1，2，3，4；为第i进口车道上右转车辆到达冲突点距离，单位为m；vc为车辆过街速度，单位为m/s。

根据人车冲突数定义，右转车辆到达冲突点时开始产生人车冲突，人车期望冲突数可表达为：

（2）行人随机过街阶段人车期望冲突数。 行人集中消散过程后进入随机消散阶段，随机消散时间可表达为：

根据泊松分布规律，随机阶段行人与车辆期望冲突数可表达为：

其中，Ppj-v为t时间内行人和车辆发生的概率；为第j人行横道车辆到达率。

综上，一个信号周期内人车期望冲突数为：

其中，、分别为第j人行横道行人集中和随机过街阶段冲突影响系数。

2.2 行人专用相位设置后交叉口人车冲突数估计模型

由于行人专用相位将行人与车辆在空间进行了隔离，两者不存在冲突，因此，行人专用相位设置后交叉口人车期望冲突数为0，即：

3 效率模型构建

3.1 行人专用相位设置前人车延误模型

（1）转弯车辆冲突延误模型。 在行人集中过街阶段，过街人群未出现车辆可穿越间隙，此时车辆冲突延误由车辆到达冲突点的时刻与人群消散过程结束时刻之间的时间间隔（） 和等待行人随机过街阶段出现车辆可穿越间隙的时间（） 两个部分组成，如图4 所示。

图4 集中阶段车辆冲突延误分析Fig. 4 Analysis of vehicle conflict and delay in concentration phase

其中，根据行人和车辆达到特性，第一部分延误受转弯车辆随机到达的影响，第二部分受可穿越间隙出现概率的影响。和的概率密度函数公式为：

行人集中过街阶段转弯车辆平均冲突延误：

其中，为转弯车辆到达冲突点的时刻与本相位绿灯结束时刻之差。

在行人随机过街阶段，车辆和行人均随机到达，转弯车辆需判断过街行人中是否出现可穿越间隙。此阶段转弯车辆延误为车辆到达冲突点和离开冲突点的时间差（），如图5 所示。

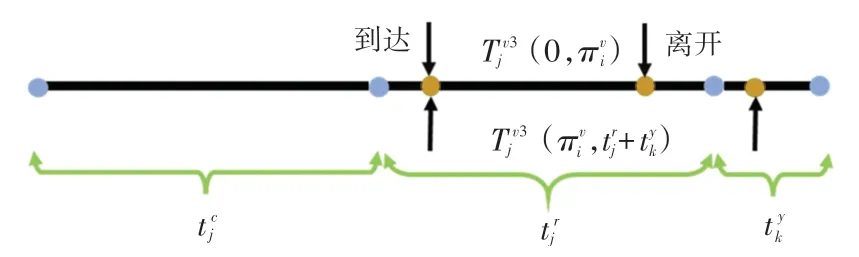
图5 随机阶段车辆冲突延误分析Fig. 5 Analysis of vehicle conflict delay in random stage

此阶段车辆冲突延误除了受车辆随机到达冲突点的影响，同行与过街行人中随机出现车辆可穿越间隙的制约。 因此，车辆冲突延误的分布和概率密度函数可描述为F（，） 和f（，）。

当车辆在本相位绿灯结束前离开冲突点，即0 ≤≤时，车辆冲突延误分布函数为：

其中，为第j人行横道上行人可穿越间隙强度，单位为ped/h。

当车辆在黄灯期间离开冲突点时，即≤≤＋，车辆冲突延误分布函数为：

其中，为第k相位黄灯时间，单位为s。

综上，转弯车辆在行人随机消散阶段产生的平均延误为：

一个信号周期内转弯车辆冲突延误为：

（2）行人冲突延误模型。 行人集中过街阶段，未出现车辆可穿越间隙，转弯车辆待人群消散完成后再行通行，故无行人冲突延误产生，即：

行人随机过街阶段，行人冲突延误为行人到达冲突点和离开冲突点的时间间隔（），其同时受行人到达冲突点和转弯车流中出现行人可穿越间隙的随机性影响。 借鉴在行人随机过街阶段转弯车辆冲突延误模型推导过程，此阶段受转弯车辆影响，行人平均冲突延误为：

其中，表示行人到达冲突点的时刻，取值为行人到达冲突点的时刻与本相位行人绿灯结束之间的时间间隔，h（，） 为行人概率密度函数。

一个信号周期内行人冲突延误：

（3）行人专用相位设置前交叉口信号延误模型。 对于交叉口信号延误，本文选取2000 版美国通行能力手册（HCM）内的交通延误公式作为人车延误计算。

车辆信号延误可由式（18）计算求出：

其中，为车辆均匀到达产生的延误，单位为s/veh；为由车辆到达的随机性而产生的增量延误，单位为s/veh；为等待上周期未通过交叉口的剩余车辆而初始排队延误，单位为s/veh。

行人信号延误可由式（19）计算求出：

其中，为第k相位车辆绿灯时间，单位为s。

3.2 行人专用相位设置后人车延误模型

由于行人专用相位的设置，交叉口行人和车辆不存在冲突，此时行人和车辆的冲突延误均为0，即：

车辆信号延误的数学公式具体如下：

行人信号延误的数学公式具体如下：

其中，为行人专用相位时间，单位为s。

4 交叉口行人专用相位适用性模型

引入单位安全成本和效率成本，建立交叉口行人专用相位设置前后优化模型。 其中，单位安全成本是指发生一次人车冲突数所产生的成本消耗，单位效率成本是指1 h 内人车延误耗时成本。

行人专用相位设置前交叉口优化目标函数为：

其中，τs为人车期望冲突数单位成本，单位为元/次；σe为每小时内交叉口交通延误成本，单位为元/h；ξ为车辆平均载客率，单位为人/辆。

行人专用相位设置后交叉口优化目标函数为：

综上，交叉口行人专用相位设置前后优化模型为：

其中，当δ＝0 时表示行人专用相位设置前，δ＝1 表示行人专用相位设置后；Cmin、Cmax分别为最小、最大周期，单位为s；、分别为行人最小、最大有效绿灯时间，单位为s；

通过对模型求解，得到行人专用相位设置前后模型最优值。 当Zbe ＞Zaf时，交叉口应设置行人专用相位；当Zbe ＜Zaf时，则不适宜设置行人专用相位。

5 案例及适用性分析

为进一步验证模型的有效性，本研究对上海市延吉东路和水丰路交叉口展开实地调研，并基于调查数据对模型进行验证，其中，人车冲突数估计模型通过理论冲突数与实际冲突数进行对比验证；行人和车辆延误模型则采用仿真进行验证。 最后，通过计算行人专用相位设置前后的交叉口运行总成本，确定案例交叉口最优的信号控制方案。

5.1 模型验证

5.1.1 人车冲突数估计模型验证

根据实地调查结果和人车冲突数估计模型，计算案例交叉口单位小时内行人和车辆实际冲突数和理论冲突数，见表1。

表1 案例交叉口实际冲突数和理论冲突数Tab. 1 Actual and theoretical conflicts at case intersections

从表1 可得出，实际发生的冲突数和理论冲突数分别为209 个和185 个，两者相对误差为11.48%，在可接受范围内，说明本文建立的人车冲突数估计模型能较为客观地反映交叉口实际的安全情况。

5.1.2 延误模型验证

通过VISSIM 仿真软件，选取随机种子值，将行人专用交叉口仿真延误值和采用延误模型计算的延误值进行对比分析，见表2。

表2 行人专用相位设置后交叉口交通延误验证Tab. 2 Verification of traffic delay at intersections after pedestrian dedicated phase setting

由表2 可以看出，3 次随机种子对应的仿真总延误分别为16.61 h、17.86 h、15.99 h，模型总延误为17.75 h，两者平均绝对误差为5.6%。 因此，通过验证分析，表明本文建立的交叉口延误模型能够较为准确地描述交叉口运行效率状况。

5.1.3 模型优化结果

根据交叉口行人专用相位设置前后优化模型，得出行人专用相位设置前后综合成本计算结果见表3。

表3 行人专用相位设置前后交叉口运行成本Tab.3 Operating costs of intersections before and after pedestrian dedicated phase setting

从表3 中可以看出，行人专用相位设置前交叉口周期为60 s，运行成本为525.6 元。 采用行人专用相位方案对现状交叉口进行优化后，得出最优信号周期为46 s，行人专用相位时间为10 s。 行人专用相位设置前后交叉口运行成本分别为525.6 元和443.5元，因此，对于案例交叉口宜采用行人专用相位信号控制方案。

5.2 适用性分析

根据实验发现，行人专用相位的设置除了与交叉口人车流量有关之外，还受车辆的转弯比和行人违章率影响。 因此，为进一步确定行人专用相位的适用范围，通过调整交通流量、车辆的转弯比和行人违章率参数数值，研究行人专用相位适应性的变化情况。

5.2.1 车辆转弯比对行人专用相位适应范围的影响

对于常规两相位交叉口来说，当转弯车辆较多时，会增加与过街行人发生冲突的概率，增加行人和车辆交通冲突延误时间。 因此，随着车辆转弯比较的不同，行人专用适用范围随之发生变化。

图6 为不同车辆转弯比行人专用相位适用范围随人、车流变化示意图。 零线上方表示行人专用相位适用范围，零线下方表示常规两相位适用范围。从图6 可以看出，车辆转弯比大于2 时，行人专用相位在人流量大于150 人/h、车流量大于300 人/h 的条件下优势逐步凸显；随着车辆转弯比的递减，行人专用相位的适应范围逐步减少，当达到1：3 时，不存在行人专用相位的设置条件，这是因为随着交叉口车辆转弯比的不断缩小，行人过街安全程度逐步上升，若此时设置行人专用相位，其产生的安全效益会低于增加一个行人专用相位时长所引起的效率成本，从而增加交叉口的整体运行成本。

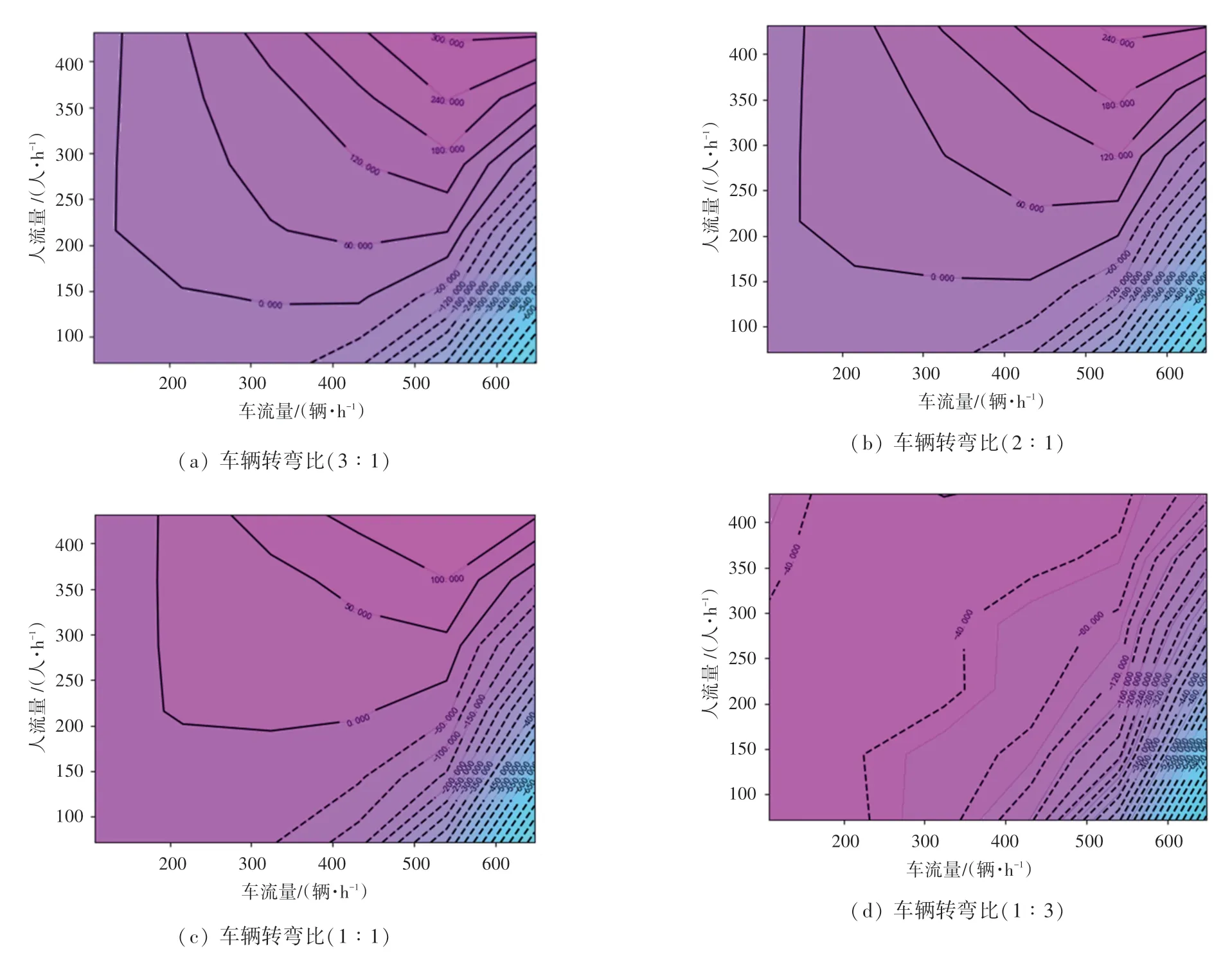
图6 随车辆转弯比变化行人专用相位适用范围变化情况Fig. 6 Changes in the applicable range of pedestrian dedicated phase with the change of vehicle turning ratio

5.2.2 行人违章率对行人专用相位适应范围的影响

由于行人专用相位的设置，交叉口信号周期时间会大大延长，行人等待过街时间也随之增加，当超过行人最大忍耐时间，行人则会选择违章通行。 过高的违章率在增加交叉口安全成本的同时，使得车辆与行人之间冲突风险不断上升，降低交叉口运行效率，缩小行人专用相位适应范围。

图7 为不同行人违章影响系数下，行人专用相位适用范围随人、车流变化的示意图。 从图7 可以看出，当违章影响系数小于1.1 时，行人专用相位在人流量大于200 人/h、车流量大于300 人/h 条件下适用性较高。 随着行人违章影响系数的上升，行人专用相位适用范围不断缩小，这是因为行人违章率的增加，使得交叉口安全成本逐步上升，行人专用相位产生安全效益不断降低。 因此，行人专用相位在行人违章率较小时更为适用。

图7 随行人违章影响系数变化行人专用相位适用范围变化情况Fig. 7 Changes in the applicable scope of pedestrian dedicated phase with the change of the impact coefficient of pedestrian violation

整体上看，行人专用相位适用性与车辆转弯比呈正比，与行人违章影响系数呈反比，且人、车流量越大，行人专用相位优势越为显著。 对于常规两相位交叉口来说，低人流量、高车流量的情况可采用此信号控制方案。

6 结束语

本研究在分析行人专用相位设置前后交叉口人车冲突机理的基础上，以人车期望冲突数为安全指标，以人车冲突延误模和信号延误为效率指标，引入安全和人、车延误单位成本构建行人专用相位设置前后交叉口适用性模型，并通过实例验证了模型的有效性，得到案例交叉口最优信号控制方案。 其次，通过数值分析确定行人专用相位适用性与车辆转弯比呈正比，与行人违章影响系数呈反比，且人、车流量越大，行人专用相位优势越为显著。 另外，在分析交叉口冲突模型时只考虑了行人与机动车冲突关系，而现实中非机动车也是常见的一种交叉口过街交通，因此在后续研究中将考虑非机动车对人车冲突数和冲突延误的影响。