基于NP和NPL模型在黄河流域的月径流模拟研究

吴昊昊，倪 晋

(1.安徽省·水利部淮河水利委员会水利科学研究院，安徽 蚌埠 233000；2.安徽省水利水资源重点实验室，安徽 蚌埠 233000；)

1 研究背景

参数模型大多数基于模型驱动，并且对于水文序列的概率分布和相关关系做了一定程度的假设。为尽可能接近于历史序列的真实分布，水文学者们提出大量非参数随机模型，从数据驱动出发，避免了参数估计以及对研究对象概率分布和相依结构的假定，能够较好地捕捉水文序列间的相依特性。

非参数核密度估计模型作为非参数模型的重要研究方向，近年来已取得较大发展。Sharma等[1]假定径流为一个具有时间依赖性的马尔柯夫过程，利用条件概率密度函数的核密度估计生成模拟径流序列，提出非参数一阶马尔柯夫模型(NP(1))。结果表明这种基于数据驱动的非参数径流合成方法，比随机水文学中使用的传统模型更灵活，并且能够再现线性和非线性相依关系。王文圣等从数据驱动角度出发，建立了单变量多阶核密度估计模型，在屏山站日径流过程模拟中证明了其适用性[2]；之后利用该模型展开金沙江流域李庄-屏山区间年径流过程的模拟研究，通过和自回归模型对比验证了非参数模型的优越性[3]。Sharma等[4]基于上述模型无法在较大的(季节性到年际性)时间滞后中保留相依关系，尤其是对观测到的分布特征如概率密度函数中强不对称或多模态性等表现不佳，使用可变核和径流聚集变量改进了NP模型，提出了一种月径流序列年际相关性的非参数模型(NPL)。王文圣和丁晶[5]尝试建立多变量非参数模型，并随机生成屏山站和宜宾-屏山区间两站日径流模拟序列，实例应用表明该模型的模拟效果较好。陈大春[7]利用粒子群算法优化基于最小二乘交叉法建立的带宽系数目标函数和可变核带宽方法，构建了非参数核密度估计模型，并应用于乌鲁木齐河月径流模拟。

考虑到NPL模型在国内的应用研究较少，且现有文献几乎未深入探讨过NP和NPL在径流模拟方面的适用性对比，本文以黄河流域兰州、龙门和白马寺3个水文站点的天然月径流序列资料为研究对象，分别建立各站点月径流的NP和NPL模型，比较分析两模型在研究区的适用效果，以期为水利工程规划设计管理提供依据。

2 模型原理

2.1 核密度估计理论

从概率密度函数f(x)未知总体中抽取独立同分布样本，当随机变量X为d维时，总体密度f(x)的核密度估计定义为[9]：

(1)

式中，X=(X1，X2，…，Xd)T；Xi=(Xi1，Xi2，…，Xid)T(i=1，2，…，n)；d—随机变量X的维数；S—向量X的d×d维对称样本协方差矩阵；K(u)—核函数；h—带宽系数；n—样本容量。

本文中选用标准高斯函数作为核函数，最小二乘交叉证实检验(LSCV)法寻求带宽系数h[10]，公式为：

(2)

式中，Lij=(Xi-Xj)TS-1(Xi-Xj)；Xi，Xj数据不同；S—数据样本协方差阵；p—模型阶数；n—数据组数。

2.2 非参数p阶马尔科夫径流模型(NP)

当xt(t=1，2，…，n)为单变量水文相依时间序列，且xt依赖于前p个值xt-1，xt-2，…，xt-p，令Vt=(xt-1，xt-2，…，xt-p)T，则xt的条件概率密度函数为[11]：

(3)

式中，fV(Vt)—p维边缘概率密度函数；f(xt，Vt)—p+1维联合分布密度函数。基于高斯核密度估计，得到：

(4)

(5)

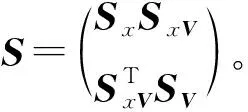
式中，S—(xt，Vt)的(p+1)×(p+1)阶对称样本协方差矩阵；Sx—xt的样本方差；SxV—xt与Vt的1×(p+1)阶样本协方差矩阵；SV—Vt的p×p阶对称样本协方差矩阵。Vt=(xt-1，xt-2，…，xt-p)T和xt来自于实测样本数据，其中t=p+1，p+2，…，n。

将式(4)、(5)代入式(3)整理得到

(6)

式中，

(7)

(8)

(9)

(10)

应用式(6)能够随机模拟序列xt，模拟公式如式(11)：

(11)

式中，et—均值为0，方差为1的独立高斯随机变量。模型阶数p根据AIC准则确定。

2.3 NPL模型

为精确表达模拟径流月份之间和年际之间的相关性，Sharma[4]提出一种季节性径流序列随机模拟方法(NPL)，它引入了确保准确描述季节与年际相关性的聚集变量和可变核，试图在模拟的径流序列中再现这种长期相关特性。

考虑时间t处的径流量为xt，例如月径流前12个月的月径流可以表示为x1，x2，…，x12，接下来的12个月可以表示为x13，x14，…，x24，以此类推。因此聚集径流变量Zt定义为：

(12)

式中，m—聚集水平，代表模拟月份过去m个月的径流量和。本文选用模型阶数p=1、聚集水平m=12进行介绍，则用于模拟的条件概率密度如下：

(13)

式中，fm(·)—变量集的边缘概率密度。用式(1)进行高斯核密度估计，变量集(Xt，Xt-1，Zt)的联合概率密度可以表示为

(14)

式中，h—带宽系数；n—样本容量；S—变量集(Xt，Xt-1，Zt)的协方差矩阵，其中S11—Xt的样本方差，S12—Xt与Xt-1的样本协方差，S1z—Xt和Zt的样本协方差，S22—Xt-1的样本方差，Szz—Zt的样本方差，S2z—Xt-1和Zt的样本协方差。

式(14)相当于n个正态概率密度函数的比例和，根据多元正态分布的已知关系，可以进一步简化为

(15)

其中，

(16)

(17)

式中，参数同式(14)意义一致。

类似地，(Xt-1，Zt)的联合密度函数估计为

(18)

式中，参数同式(14)意义一致。将式(15)和式(18)代入式(13)，整理可得

(19)

其中，

(20)

式中，bi—与每个内核相关联的条件平均数，如式(16)所示；ωi—构成条件概率密度每个核相关的权重；其他参数同式(14)意义一致。

应用式(21)能够随机模拟序列Xt，模拟公式为：

(21)

式中，Et—均值为0，标准差为1的高斯随机变量。

由于高斯核函数自身具有对称无界特点，可能会大量导致部分负径流值的生成，对模拟序列造成边界影响。NPL模型采用可变核修正方法对带宽系数进行优化，具体修正步骤见文献[13]。

3 实例应用

3.1 资料的选取与审查

本文以黄河流域兰州、龙门和白马寺3个水文站点的天然月径流序列资料为研究对象，开展NP和NPL模型在径流模拟中的应用研究，水文数据均满足可靠性、代表性和一致性要求，可用于模型的相关分析计算。

3.2 模型参数

各站点的模型阶数根据AIC准则识别，经计算兰州、龙门和白马寺的模型阶数取p=1，因此建立黄河流域3个水文站点的一阶NP和NPL模型应用于月径流随机模拟。根据式(2)采用优化方法最小化LSCV求得NP和NPL模型各站点各月优化带宽h，结果见表1。

表1 NP和NPL模型各站月径流序列各月优化带宽h估计

3.3 模型检验和对比分析

本节采用短序列法检验模型适用性，针对3个水文站点分别生成300组样本，每组样本容量对应站点序列长度。为探讨分析模拟效果，NP和NPL模型的适用性检验和对比分析利用均值、标准差、偏态系数等统计值，部分统计特征参数如图1—5所示，见表2—4。

图1 各站NP和NPL模型均值

表2 兰州站NP和NPL模型月径流统计特征值

表3 龙门站NP和NPL月径流统计参数

表4 白马寺站NP和NPL月径流统计参数

由图1可得：均值方面，兰州站NPL模型模拟效果要优于NP模型，而在龙门站和白马寺站，NP模型模拟序列的各月均值要更接近于实测序列，在部分月份NPL模型模拟效果不佳。分析表2—4中的均值统计特征能够得到：兰州站NPL模型均值未控制在两个均方差标准下的月份达50%，有33%的月份均值在一个均方差标准下；NP模型超出2个均方差标准下的月份比例要略低于NPL模型，表明对于兰州站NP模型和NPL模型的模拟序列没有很好地保持实测的均值统计特性。龙门站NPL模型有50%的月径流模拟序列均值未能控制在两个均方差下，控制在一个均方差标准下的月份达33%；NP模型模拟效果要优于NPL模型，有50%的月径流模拟序列控制在一个均方差下。白马寺站NP模型除3月和4月外其余月份的均值均控制在一个均方差下，而NPL模型未能控制在两个均方差标准下的月份占41%，总体上来看NPL在均值统计特性方面模拟效果不如NP模型。

如图2所示，标准差方面，在兰州站、龙门站和白马寺站，非汛期NP和NPL模型模拟序列的标准差与实测序列基本能保持一致，汛期NP模型表现更好，实测序列的标准差处于模拟样本中位数附近浮动。结合表2—4中的标准差统计特征能够得到：兰州站NP模型占75%的月份均值能控制在一个均方差标准下，相比NPL模型能够控制在两个均方差标准下的月份仅占25%，表明NP模型相比较更适合兰州站用于径流模拟。龙门站两模型模拟序列标准差除个别月份基本都能较好的控制在两个均方差标准下，与实测序列的统计特征值差距较小。白马寺站NPL模型模拟序列均值控制在两个均方差标准下的月份占41.7%，NP模型除3月份其余月份均控制在2个均方差标准下，说明白马寺站NP模型相比NPL模型对历史实测序列的标准差统计特征保持得更好。

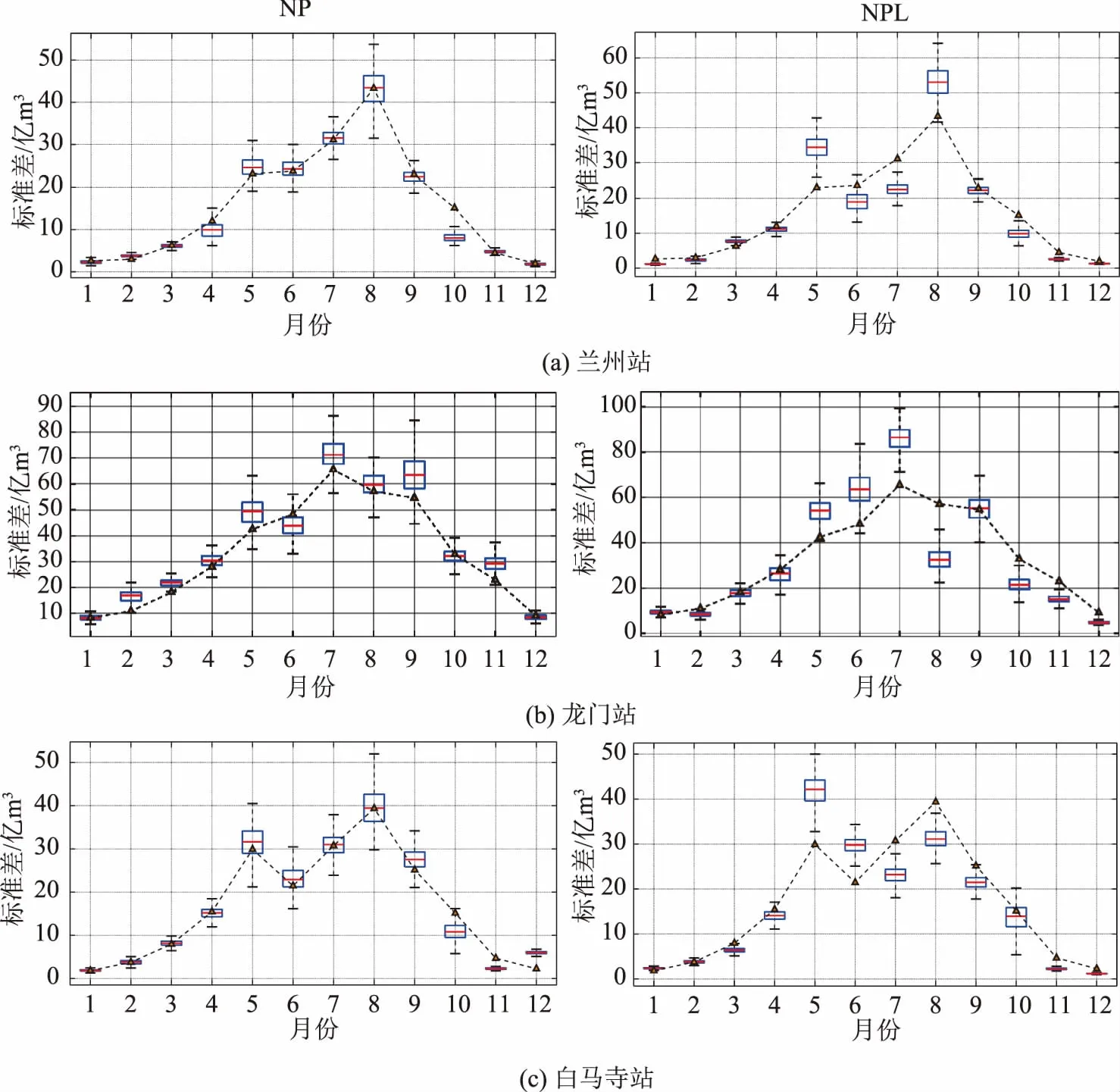
图2 各站NP和NPL模型标准差

由表2—4中的偏态系数统计特征能够得到：兰州站NPL模型无法控制在两个均方差标准下的月份达50%，NP模型除8月外其余月份均能控制在两个均方差标准下，模拟效果更加理想。龙门站NPL模型的偏态系数在大多数月份能够控制在两个均方差标准下，NP模型除1月、2月和3月外其余月份均良好地保持在一个均方差标准下。白马寺站NPL模型超出两个均方差标准的月份达41.7%，NP模型有75%的月径流序列偏态系数控制在两个均方差标准下。

由两个模型的二阶自相关系数图(如图3所示)和表2—4中的R1和R2统计特征能够得到：R1方面，NP模型和NPL模型模拟序列的统计特征值与实测序列R1均有较大偏差；根据计算NPL模型各站点的模拟序列一阶自相关系数控制在两个均方差标准下的月份占58.3%及以上，NP模型在兰州站和白马寺站基本保持R1统计特征的月份为58.3%左右。R2方面，模拟效果总体要优于一阶自相关系数，兰州站NP模型各月份的R2基本位于盒箱范围内，而NPL模型模拟效果不佳。根据表中数据计算，发现兰州站NP模型控制在两个均方差标准下的月份比例比NPL模型要高16.7%，龙门站两模型基本相似，白马寺站NPL模型控制在两个均方差标准下的月份比例要高8.3%，与箱型图结果基本一致。总体来看，对于各站NP和NPL模型二阶自相关系数的模拟效果要优于一阶。

图3 各站NP和NPL模型二阶自相关系数R2

图4说明了滞后1个月月径流量与之前12个月的总径流量之和之间的相关性。总的来看，在滞后一个月的情况下，NPL模型比NP模型较好地再现了这些相关性，如兰州站的12月，龙门站的1月、2月，白马寺站的10月等。但在白马寺站部分月份和其余站点的个别月份，两模型均有与实测径流序列统计特征值差距较大的情况发生。滞后2月观察到类似的结果，这表明在NPL模型模拟中，长期依赖性得到了恰当的表示。

图4 各站NP和NPL模型滞时为1的月年互相关系数

图5采用直观地根据概率密度函数形态检验模拟径流序列是否服从实测径流序列分布，根据原序列概率密度分布图选取具有代表性(如平顶性、多模态性和偏态性)的月份展示NP和NPL模型模拟效果。对比发现NPL模型在再现原序列概率分布的偏态性时更加贴近于实测序列，尽可能地再现了原径流序列概率密度分布的不对称性，如兰州站的3月、白马寺站的9月等；针对如兰州站的8月、龙门站的3月以及白马寺站的3月等表现的平顶性，NPL模型相比NP模型较好地重现了上述统计特性。但也发现在NP和NPL模型在模拟一些月份时效果不佳，这可能是因为高斯核函数的光滑性和对称性而导致的。

图5 各站NP和NPL模型代表性月份边缘概率密度函数图

4 小结

本文以黄河流域兰州、龙门和白马寺3个水文站点的天然月径流序列资料为研究对象，建立了各站点月径流的NP和NPL模型，对比分析两模型的适用性，得到主要结论如下。

(1)对于均值、标准差而言，总体来看NP模型模拟效果要优于NPL模型，各站点模拟序列的各月统计特征大多数要更接近于实测序列。

(2)对于偏态系数而言，NPL模型各站11月、12月的模拟效果较差，NP模型各站点的月径流模拟序列的偏态系数基本能与实测序列相似。

(3)对于一阶和二阶自相关系数而言，总体来说对于各站NP和NPL模型二阶自相关系数的模拟效果要优于一阶。

(4)在滞后1个月和2个月的月径流量与之前12个月的总径流量之和之间的相关关系方面，滞后1月和滞后2月的结果近似，NPL模型比NP模型较好地再现了这些相关性，表明在NPL模型模拟中，长期依赖性得到了恰当的表示。

(5)根据模拟序列密度函数形态检验径流序列服从实测径流序列分布结果，得到NPL模型在再现原序列概率分布的偏态性和平顶性时更加贴近于实测序列，较好地再现了原径流序列概率密度分布的不对称性。