基于实测数据的阵列式组件装配调控技术

杨业涛，林雪竹，2，郭丽丽，2，李丽娟，2

（1.长春理工大学 光电工程学院，长春 130022；2.长春理工大学 中山研究院，中山 528403）

随着科技的创新发展，重要产品的性能保障由开始的设计、制造环节逐渐向装配环节发生转变。阵列式组件作为应用在飞行器上的一种防热结构，保护飞行器不会受到因与大气层摩擦而产生的热量的损害，其装配质量对于飞行器的安全有着十分重要的作用［1］。据文献所述，传统阵列式组件的装配以人工为主，数字化测量设备用于辅助检测装配质量。由于制造偏差、缺乏定位基准以及人员装配误差使得阵列式组件的装配不能满足装配精度，因此需要不断地试装直到装配质量合格，这样不仅会损伤阵列式组件，装配效率也相对低下。因此，建立定位基准、减少制造偏差影响以及降低人员装配误差对于阵列式组件的装配具有十分重要的作用。

近几年兴起的数字孪生作为虚实空间相映射的技术为装配提供了技术手段和解决方法，使得产品装配制造过程实现了技术升级。目前，国内外研究学者们对将数字孪生应用在产品全周期各个环节进行了大量的研究，Zhuang 等人［2］提出了针对于复杂产品装配过程的数字孪生智能生产管理与控制方法，并基于该方法设计了数字孪生技术驱动的装配控制系统。陶飞等人［3］提出了基于数字孪生技术的车间运行机制以及实现该机制所需的关键技术与特点。赵浩然等人［4］针对孪生车间的应用，提出了一种针对产品装配过程的可视化实时监控的方法。周石恩［5］针对薄壁件的装配问题提出了一种基于数字孪生技术的产品定位-装配精度预测方法，并且将其应用于反射面天线阵面装配精度分析中。Polini 等人［6］在复合材料装配制造工艺的轻量化设计中引入数字孪生技术，实现了全生产周期的几何偏差信息管理。Sun 等人［7］在高精密机械产品的装配调试问题中引入数字孪生技术，提出了产品装配精度预测和装配工艺优化的相关对策，确保了高精度机械产品的最终装配质量。

综上所述，数字孪生技术在物理装配实体与虚拟装配模型之间建立了联系，在产品装配工艺设计阶段加入了装配现场的实测数据，构建了与装配实物一致且相互映射的虚拟模型，实现了在线模拟仿真并准确预测产品装配精度和装配性能，提高了产品实际装配质量以及效率。因此本文将数字孪生技术引入阵列式组件装配中，构建以实测数据为输入的孪生模型，并研究虚拟空间中装配参数的求解模型。分析装配参数并建立装配优化模型，获取阵列式组件装配定位基准。构建数字装配平台测量装配定位基准以实现对阵列式组件物理装配的调控，通过虚拟映射实现对实际装配过程中的综合考虑，提高了阵列式组件装配效率与质量。

1 基于实测数据的阵列式组件装配调控框架

为了解决阵列式组件的装配问题，提出了基于实测数据的阵列式组件装配调控框架，总体流程如图1 所示。

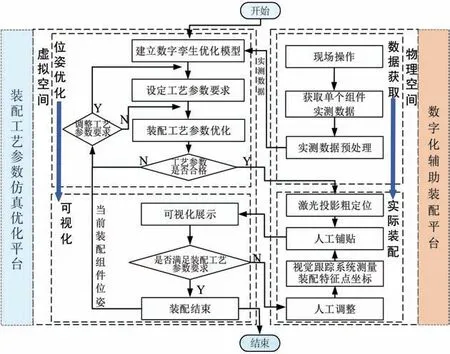
图1 面向数字孪生的阵列式组件装配调控总体流程图

以数字孪生技术为核心，首先，在虚拟空间中基于阵列式组件的实测数据构建装配参数求解模型，并对装配工艺要求进行设定，以装配参数为目标函数，利用FBI（Forensic-based Investigation）算法对组件的位姿进行优化，优化后各组件的位姿将用于指导物理空间的装配。其次，在物理空间中构建数字化辅助装配平台，通过3D 投影系统实现对组件的基本定位，视觉跟踪系统实时感知组件的位姿，人工对组件的位姿进行调整。最后，将装配合格的组件位姿数据传递到虚拟空间中，作为有约束的固定组件，对其他未装配的组件位姿进行优化迭代，迭代结束继续指导装配。在虚拟空间中对基于实测数据的组件装配可行性进行计算与仿真，若满足装配工艺参数要求，则物理空间进行装配，否则需要根据优化结果对装配工艺参数要求进行调整。

为了更加准确地表征阵列式组件的位姿，在获取实测数据之前，在阵列式组件上人为地、有规律地粘贴装配特征点用于表征阵列式组件的位姿，且特征点与阵列式组件之间的相对位置不会随着时间的变化而发生变化。

2 阵列式组件装配参数模型构建及位姿优化

由于制造工艺的影响，实际制造的阵列式组件与理论模型存在一定的偏差，以理论模型为目标进行仿真优化难以反映实际装配情况，为了实现虚拟空间对物理空间的装配指导，需要在虚拟空间中对阵列式组件的装配进行仿真。因此以阵列式组件的实测数据作为输入，在虚拟空间中构建影响阵列式组件装配质量的参数求解模型，并将装配参数作为目标函数，使用FBI 算法对阵列式组件的位姿进行优化迭代，从而得到阵列式组件装配参数的可行解，用于指导实际装配，其中阵列式组件的实测数据包括组件的外形点云以及装配特征点。

2.1 构建装配参数求解模型

影响阵列式组件装配质量的参数主要为两个相邻组件之间的间隙与阶差。

相邻组件之间的间隙阶差是处于垂直于缝隙的平面上的两个组件特征点之间的水平与垂直距离。因此间隙阶差的求解可以分为三个步骤：断面求取（垂直于缝隙处的平面）、特征点求取以及间隙阶差求取，间隙阶差求解流程图如图2 所示。

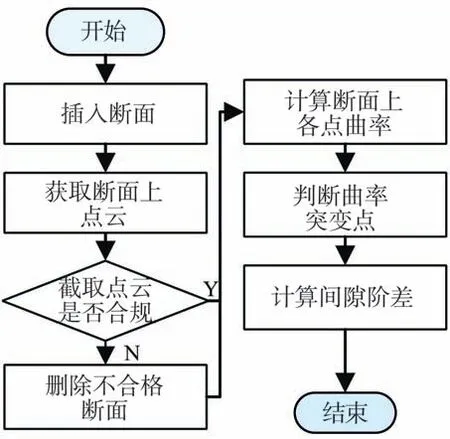
图2 间隙阶差求解流程

在实测数据获取的过程中由于检测误差不可避免会存在一些杂散点，因此需要对实测数据进行数据预处理。为了缩短优化迭代时间，需要对齐实测数据，使其处于理论坐标下。

2.1.1 断面求取

断面求取首先需要确定组件的边缘特征区，即进行边缘检测，确定组件靠近组件上表面边缘。基于曲率密度的局部边缘检测的方法不仅能够增强点云局部区域表达，还能降低计算的复杂度，能够很好地将边缘特征区域提取出来，因此采用该算法将组件的边缘特征区提取出来用于断面的求取。

为了确定断面上一个点以及法向量，对组件的边缘特征区进行体素化，用边长为r的网格单元将其进行划分。求取每个网格单元的中心点，每格长度为l（l为r的n倍）的区域内，所有网格中心点拟合为一条直线，将其作为断面的法向量。选取该区域网格单元的中心网格的中心点作为断面的中心点，断面求解具体示意图如图3 所示。

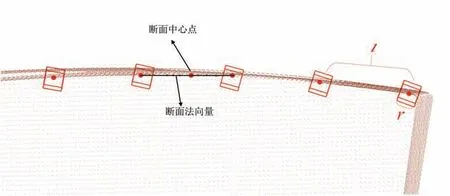
图3 断面求取示意图

由于断面位置的不同，截取的点云的形状也不完全一样，因此会产生不合格的点云，合格与不合格点云具体如图4 所示。不合格的断面将其删除，合格点云的断面则进行下一步骤。

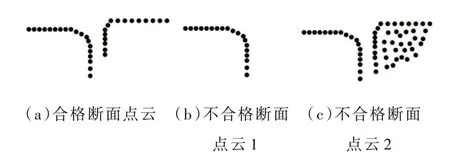
图4 断面点云示意图

2.1.2 特征点选取

由于相邻组件之间的间隙阶差定义的不同，将特征点分为间隙特征点与阶差特征点。断面截取的点云包括组件上表面的一部分、组件过渡角以及组件侧面一部分的点云。根据间隙阶差的求取理论，截面上点的曲率发生突变的点作为特征点，特征点选取如图5 所示。图5 中红色点代表阶差特征点，绿色点代表间隙特征点。

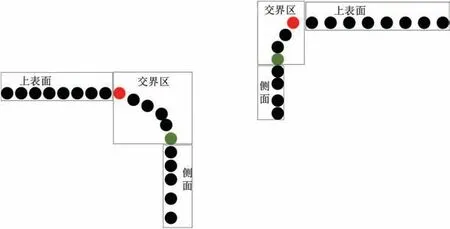
图5 特征点选取示意图

一种基于离散邻近两点之间相对位置的曲率计算方法，对于离散点曲率估算是准确的，将此作为离散点曲率计算的依据。

对于连续的图形轮廓曲线可用弧长为s的参数方程表示为：

根据曲率计算公式分别求出在点s0处的一阶导数和二阶导数，则点s0处的曲率为：

式中，k表示点s0的曲率；x'(s0)与y'(s0)表示点s0的一阶导数；x″(s0)与y″(s0)表示点s0的二阶导数。

将本文的点表示为一组互相不重合的有序点列Qi(xi,yi)，i= 0,1,…,n曲率计算示意图如图6所示。

图6 曲率计算示意图

依次连接相邻三个点，利用弦长近似表示为该处的弧长，可得到离散点Qi处曲率计算公式为：

式中，SΔQi-1QiQi+1为三角形Qi-1QiQi+1的有向面积。

通过选取一些拟合曲线效果较好的点，利用曲线曲率计算公式以及离散点曲率计算公式两者得到的曲率进行对比，误差较小，验证了离散点曲率计算公式的正确性。

2.1.3 间隙阶差求取

为便于计算间隙与阶差，将断面上点云由三维空间通过平移旋转变为二维平面上的点。断面上点云上表面近似为一条直线，因此将断面上目标点云上表面拟合为一条直线，通过平移旋转将其与二维平面x轴重合，其他点随着一起变换，便于最终间隙阶差的求取，间隙阶差求解如图7 所示。

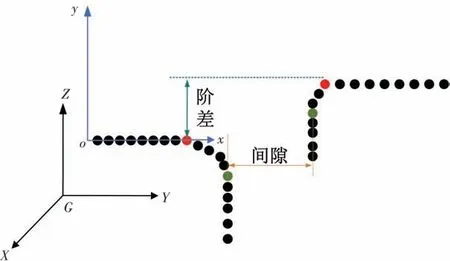
图7 间隙阶差求解示意图

其中红色点表示阶差特征点，绿色点表示间隙特征点，坐标系{G}表示全局坐标系，坐标系{O}表示各个断面上的二维坐标系。

在二维坐标系下，每个断面中间隙的求取为间隙特征点之间水平特征点的绝对值；而对于阶差来说，根据航空制造工程手册，当参考点云的特征点高于目标点云的特征点时阶差值为正值，否则为负值。

2.2 基于FBI 算法的装配参数优化

以每个组件的中心为原点建立组件局部坐标系{M}，将组件相对于局部坐标系{M}的平移量和旋转量即C=()Δx,Δy,Δz,Δθx,Δθy,Δθz作为调姿参数进行组件位姿优化。调姿后组件i中第j个点在全局坐标系{G}下的坐标为：

式中，PGij表示该点优化前在坐标系{G}下的坐标值；PMij表示优化前坐标系{M}下的坐标值；T1表示坐标系{M}相对于坐标系{G}的平移矩阵；P'Gij表示优化后该点在坐标系{G}下的坐标值；RM与T2表示组件在优化过程中的旋转和平移矩阵。

优化如图8 所示。

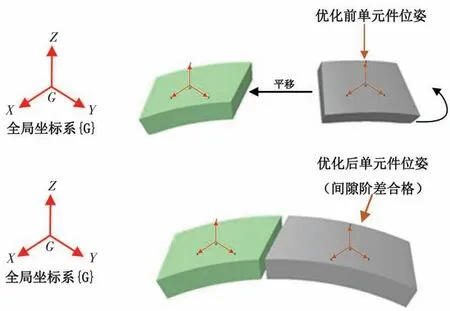
图8 优化示意图

将间隙阶差的理论要求与实际求解结果的差值作为优化算法约束条件与目标函数，二者之间的差值越小优化结果越好。因此将优化解与目标值的差值作为目标函数，即：

式中，gN、fN表示间隙阶差的名义值；gkhi(v)、fkhi(v)表示组件k与h之间第i个断面的间隙与阶差值。

法医调查算法于2020 年提出，主要模拟警察对犯罪嫌疑人的调查、定位、追踪过程。相对于其他优化算法，FBI 算法收敛速度快、寻优精度高，具有较好的探索和开发能力。为了能将位姿优化时间缩短，选用FBI 算法对目标参数进行优化，FBI 算法具体流程图如图9 所示。

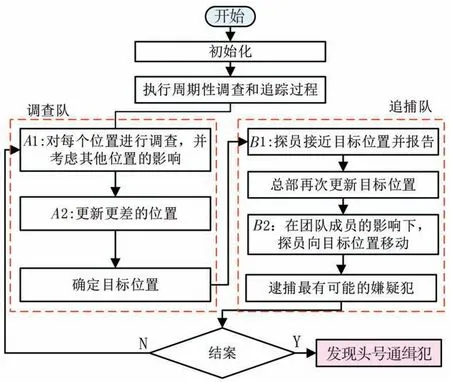
图9 FBI 算法原理

本小节以组件相对于局部坐标系{M}的平移量和旋转量作为调姿参数，而FBI 算法需要依据初始化的种群作为寻优目标，因此将FBI 算法初始化的种群数量为n× 6（n为组件的数量）。具体优化过程为：

（1）初始化种群数量、最大迭代次数、适应度函数以及其他约束条件。

（2）单元件通过调姿参数进行旋转和平移，计算间隙阶差，根据间隙阶差计算适应度值。

（3）根据适应度值的大小确定可疑位置，并继续迭代。

（4）找到适应度最小的位置作为可行解，并与装配工艺参数进行对比，符合装配功能各异参数，将其输入，否则需要改变设定的装配工艺参数，并重新进行迭代。

装配参数优化流程图如10 图所示。

图10 装配参数优化流程

优化结束之后，输出每个组件装配特征点的具体坐标值，每个组件进行物理装配时，将其虚拟空间中得到装配特征点的坐标值进行位姿调整。

3 阵列式组件可视化装配调控实例

3.1 构建软硬件系统

为有效地实现基于实测数据的阵列式组件装配调控技术，设计了装配工艺参数仿真优化平台和数字化辅助装配平台。在装配工艺参数仿真优化平台上，以阵列式组件的实测数据为优化对象，确定装配工艺参数要求，并以可视化的形式有效指导现场装配。

数字化辅助装配平台设计由C-Track 扫描仪、激光跟踪仪、激光3D 投影仪以及视觉跟踪测量系统组成。C-Track 扫描仪采集组件的外形数据，激光跟踪仪实现坐标系统一。为了能更加快速地找到每个组件的装配位置，使用激光3D投影仪实现装配的粗定位。视觉跟踪测量实时跟踪测量装配特征点的坐标，将软件系统得到的装配特征点坐标作为理论目标，实时测量装配特征点实际坐标值将其反馈到软件系统中，进行对比实现调控，装配软硬件搭建如图11 所示。

图11 装配软硬件布局示意图

3.2 装配虚实交互

为了更加直观地显示装配过程，实时显示阵列式组件的实际装配位姿。以装配可视化形式展示阵列式组件的位姿，在装配过程中，视觉跟踪系统实时跟踪测量表征阵列式组件装配位姿的装配特征点坐标值，并将坐标值以txt 格式的文本传送到装配工艺仿真优化平台。平台显示出装配特征点的仿真值与实时测量值以及两者之间的差值，人工在进行实际装配时，将软件系统的反馈，即两表之间的差值作为调整组件位姿的依据来进行装配。如此循环往复，直到两者之间的差值足够小则停止调控，装配虚实交互如图12 所示。

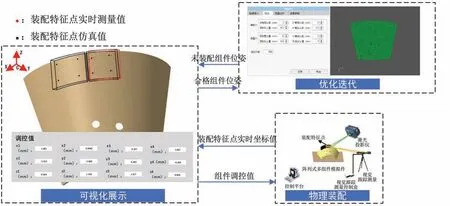
图12 装配虚实交互示意图

人工装配定位的组件位姿与仿真结果存在一定的误差，为了减少后面的误差累计，当该组件装配定位之后，需要将该组件的当前位姿传递到虚拟空间，作为固定组件，对其他未装配组件进行位姿优化迭代，更新未装配组件的位姿，进而指导装配。

3.3 实验过程与结果

为验证所提阵列式组件装配调控方法的可行性，根据阵列式组件的结构特点设计并加工阵列式组件模拟件。利用实验室现有设备搭建硬件系统，并对自行设计的阵列式组件进行装配。阵列式组件外形点云数据通过激光扫描仪MetraSCAN 3D 获取，在9.1 m3的空间范围内，其扫描精度为0.064 mm，使用API 激光跟踪仪建立全局坐标系，精度为5 μm/m；使用激光投影仪实现粗定位，精度为0.038 mm（5.1 m×5.1 m）；使用VXtrack 视觉跟踪测量系统实现对装配特征点的跟踪测量，单点重复性测量在16.6 m3的空间范围内，其扫描精度为0.02 mm。装配特征点使用能被视觉跟踪系统识别的高反光定位点，物理装配具体如图13 所示，图13（a）为实际装配过程，图13（b）为阵列式组件模拟件，模拟件上黑色反光点为装配特征点。

图13 物理装配效果图

设计阵列式组件模拟件之间的理论间隙为2 mm、理论阶差为0，其理论间隙允许公差为±0.6 mm，理论阶差允许公差为±0.4 mm。阵列式组件装配定位后，选取其中两块组件通过视觉跟踪系统测量装配特征点坐标与基于阵列式组件实测模型位姿优化后的坐标进行对比，结果如表1 所示，其中编号为模拟件上装配特征点的编号，偏差与总偏差均由均方根求得。通过外部辅助测量手段获取对应缝隙相同位置处的间隙与阶差数值，对比结果如表2 所示，表中编号为组件间断面的编号。其中对比测量工具为Lasergauge HS702-F20 激光间隙枪，测量精度为0.02 mm。当总体偏差在0.1 mm 的范围内时，间隙阶差的仿真值与实测值差值维持在±0.05 mm 范围内，满足阵列式组件装配定位精度要求。

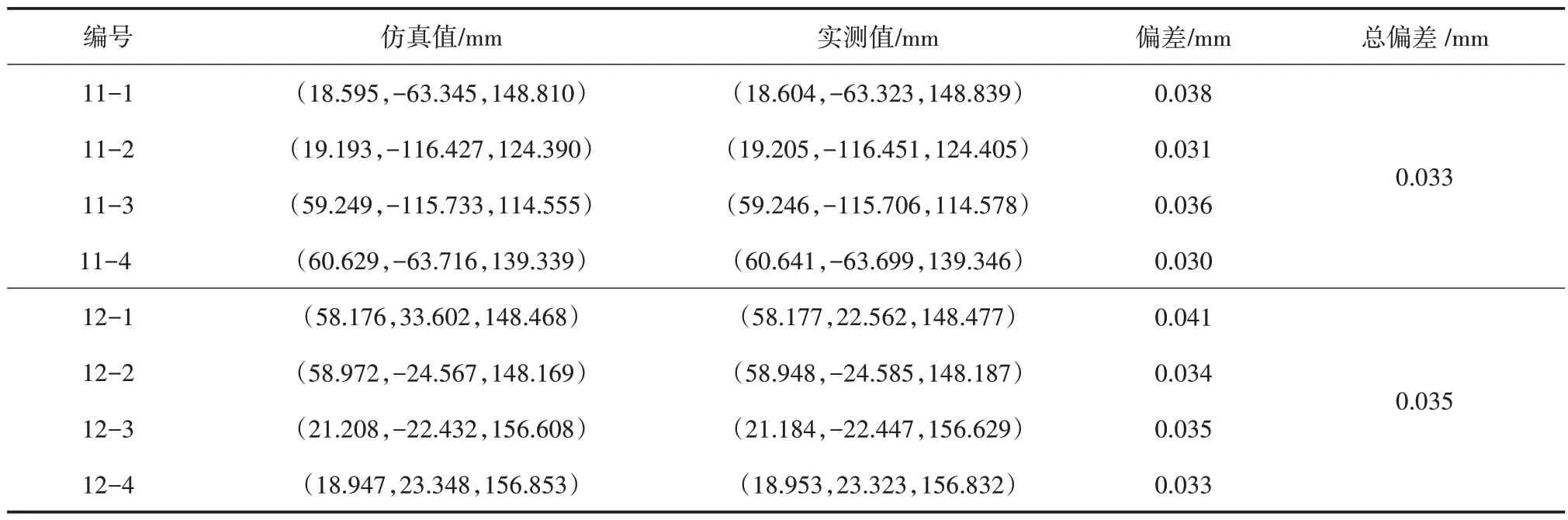
表1 装配特征点坐标值对比结果

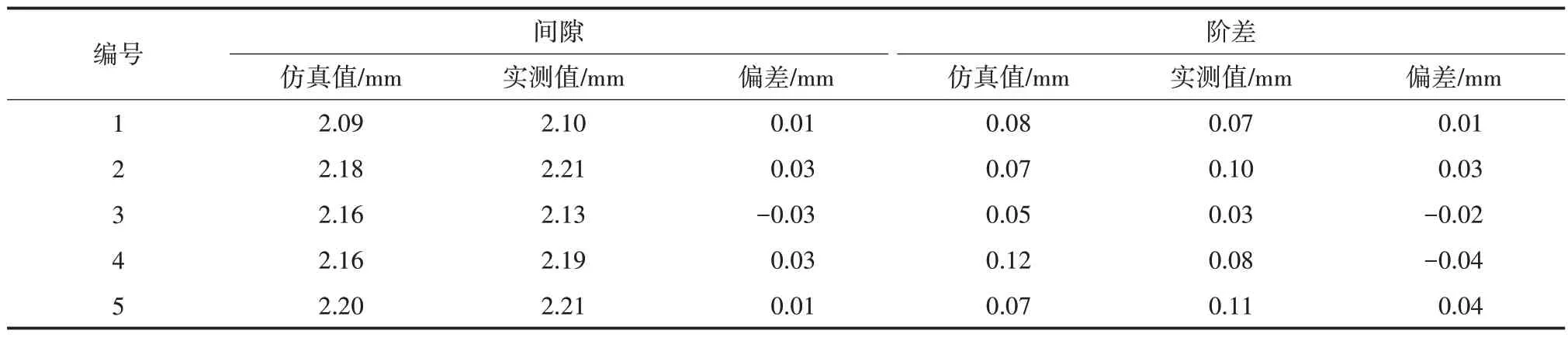
表2 间隙阶差对比结果

4 结论

本文提出基于实测数据的阵列式组件装配调控技术，以阵列式组件的外形实测数据为输入构建虚拟模型，通过算法优化组件位姿，最终以位姿优化结果作为实际装配的指导。构建硬件平台最终实现对阵列式组件的装配调控。设计阵列式组件模拟件，通过实验证明基于实测数据的阵列式组件装配调控技术的可行性，减少了阵列式组件的试装以及调整时间，提高了装配精度以及装配效率。