新一代载人飞船气动外形设计与优化

郭 斌，杨 雷，倪 庆，罗太超

(1. 北京空间飞行器总体设计部，北京 100094；2. 中国航天员科研训练中心，北京 100094)

0 引 言

新一代载人飞船需要具备执行近地和深空探测任务的能力。因此,要求新一代载人飞船返回舱具备以第二宇宙速度再入返回的能力[1]。当其以第二宇宙速度(10.8 km/s)再入地球大气时,会遇到比近地轨道再入返回更严峻的气动环境,这些问题的解决与否将关乎任务的成败。主要体现在以下两方面:首先,对于大尺寸载人航天器而言,第二宇宙速度再入返回时带来的辐射热相比近地轨道再入返回增加一个数量级,从而需要付出更大的重量代价进行热防护,因此需要通过气动外形优化有效改善再入热环境;其次,考虑到航天员承受过载极限,需要通过跳跃式再入方式减少再入峰值过载,因此需要设计更高升阻比的气动外形,提高飞船跳跃式再入返回的控制效率。

因此,新一代载人飞船返回舱气动设计重点为降低再入热环境以及提高升阻比。考虑到传统气动外形分析工况多,变量耦合严重,直接通过数值模拟遍历几何参数的方式非常耗时。本文提出通过在设计几何参数范围内选取样本点建立近似模型,并通过多目标优化气动外形[2-6]。

1 国内外天地往返运输飞行器气动外形概述

美国MPCV(多用途载人飞行器)主要用于运送乘员到达国际空间站以及地球轨道以远的太空区域,具备支持月球、近地小行星和火星探测能力[7]。该飞行器由返回舱和服务舱组成,其返回舱的气动布局经过了4轮设计,尝试了不同的倒锥角和最大直径截面直径尺寸,第4轮外形基本为阿波罗返回舱外形的放大外形(图1所示)。

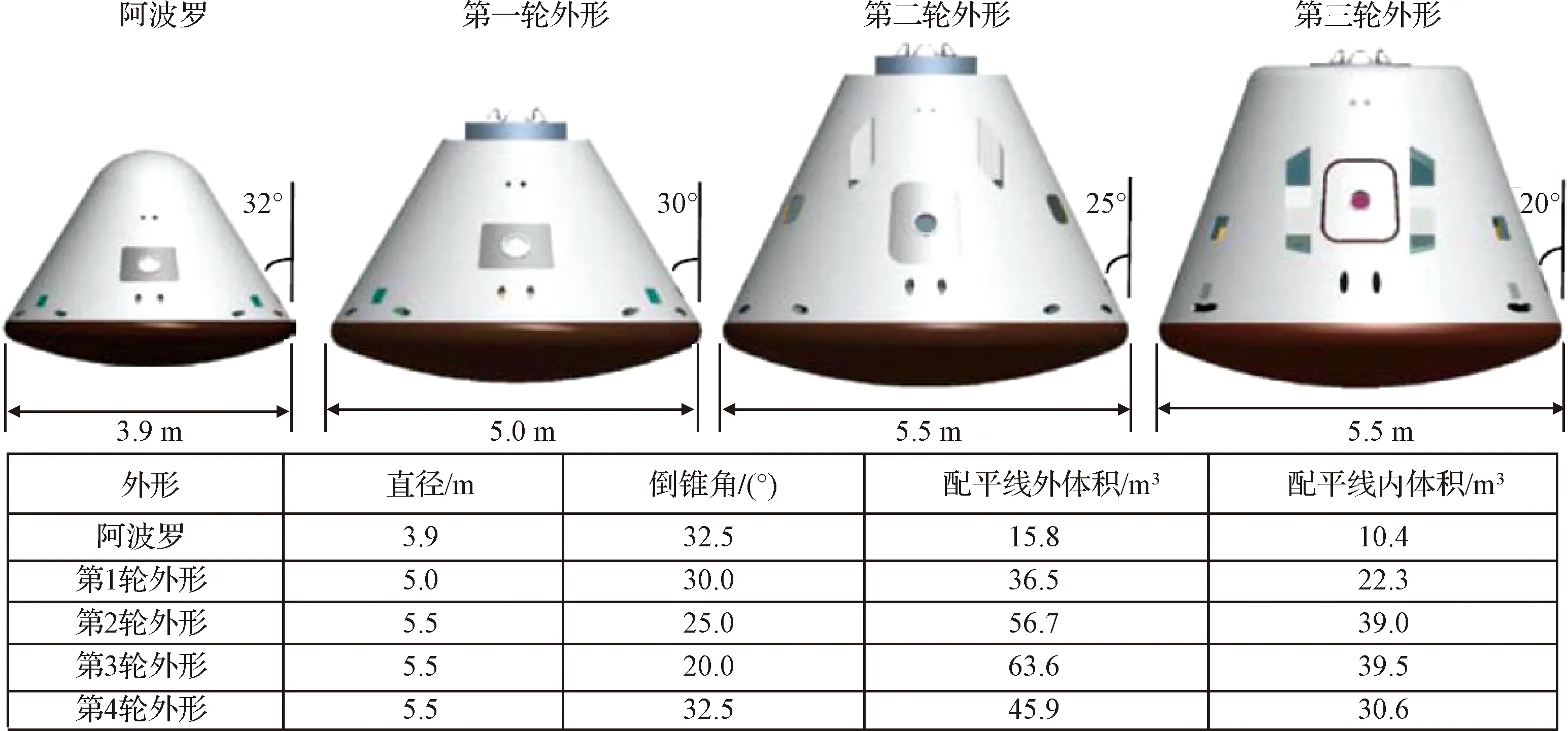
图1 MPCV返回舱气动外形发展历程Fig.1 Development of aerodynamic shape of MPCV reentry capsule

NASA于2009年提出商业乘员开发(CCDev)计划[8-9],目前共有SpaceX公司的“龙”飞船[10-11]、波音公司的CST-100飞船[12-13]、内华达山脉公司的“追梦者”太空飞机[14-16]3种载人航天器获得该项计划的支持。这3种载人航天器均执行近地轨道空间站任务,其中“龙”飞船和CST-100返回舱为钝头体外形,“追梦者”飞船为升力体外形见图2。

图2 NASA CCDev计划中的3种载人航天器气动外形Fig.2 Aerodynamic shapes of the three manned spacecraft developed in NASA’s CCDev program

俄罗斯PTK NP飞船[17]采用传统的返回舱+服务舱两舱构型,返回舱为钝头体气动外形,主要用于载人月球探测任务,并能够完成近地任务。俄罗斯PTK NP飞船由返回舱和推进舱组成,发射质量20 t,最大高度8.3 m,最多载6人,其返回舱外形依然采用了传统的钝头体外形见图3。

图3 PTK NP返回舱气动外形Fig.3 Aerodynamic shape of PTK NP reentry capsule

国外在研的5种新一代载人航天器中有4种采用了钝头体外形,只是具体几何尺寸略有不同。例如现在执行月球探测任务的MPCV,为了追求更高的升阻比,继承了阿波罗时期的32.5°倒锥角,而以执行近地任务为主的“龙”飞船,则选择了容积率更高的15°倒锥角。综合分析,国外新一代载人飞船的返回舱依然以钝头体外形为主,根据总体需求不同而调整相关几何参数。

2 气动外形选形

2.1 气动外形选形思路

天地往返运输飞行器气动外形的设计思路主要分为样本空间计算和优化气动外形两部分(具体如图4所示)。利用气动力、热和弹道工程估算的方法建立样本空间,之后利用Isight进行单目标和多目标优化,进而确定优选外形。

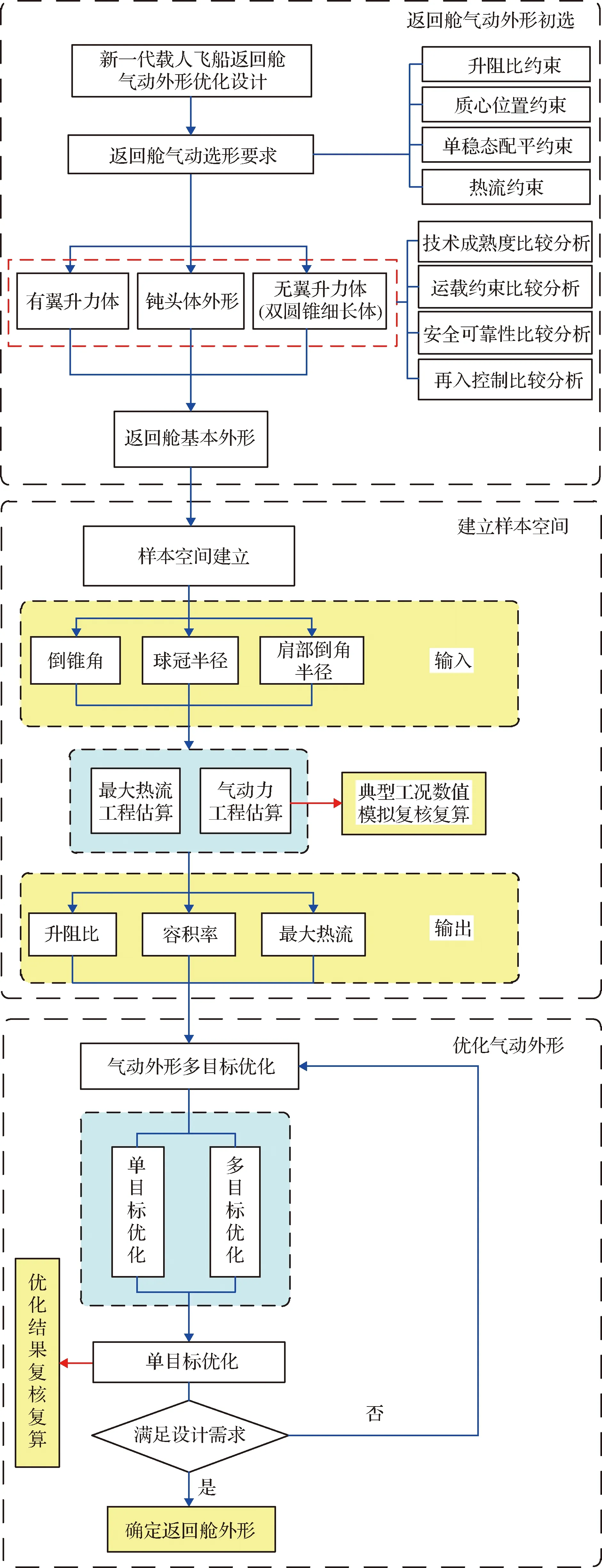
图4 气动外形选形思路Fig.4 Aerodynamic shape selection concept

2.2 气动外形初选

气动外形研究对再入返回航天器的研制起着先导和制约作用。目前国外再入返回航天器气动外形设计主要有钝头体、有翼升力体、无翼升力体3种。

美国MPCV论证过程中对返回舱气动外形的选择[18],主要给出了3个对比指标及权重[6-7]:研制成本(0.5),容积利用率(0.3),峰值过载/加热量(0.2)。对可选的气动布局典型外形(钝头体、双锥体和升力体)进行了两两打分对比。对于最少研制成本这一指标,研发费用少得1分,研发费用多得-1分,研发费用相同为0分(如表1所示)。例如,在研制成本的对比分析中,钝头体研发费用最低,升力体研发费用最高。在考虑各指标的权重系数之后,各布局类型初选分析的最后得分及排名如图5所示。其中钝头体外形的得分最高,为0.8,其次是双锥体外形,得分0.6,排名最低的是升力体外形,得分为-1.2。

图5 MPCV返回舱选形分析总分比较Fig.5 Comparison of the total score of MPCV shape selection analysis

对于升力体外形而言,面临以下问题:

1)再入航天器以第二宇宙速度再入大气时,翼面、气动舵面等部位前缘会遇到气动加热过载过大问题。对于带翼航天器,翼尖厚度小,再入过程中处于迎风绕流面,热流密度峰值和总加热量都很高,这些活动部件的所处位置气动加热环境较为恶劣,热防护设计面临较大挑战。

2)高超声速下使用的气动舵面的复杂控制难度大,技术积累薄弱,研制成本高、研制周期长。一方面,大升力体带翼航天器舵面控制对于气动数据的准确性要求高,而在高速再入过程中,稀薄流区气动数据库偏差较大,因此要通过舵面实现精确姿态控制难度很大。

3)尾翼、垂直翼面、气动舵等仅在进入大气层的再入段使用,但之前要一直经历环月球或其他天体飞行,直到任务完成,给航天器推进增加很大的负担。对于载人深空探测任务而言,再入段使用的气动舵、翼在整个飞行任务中仅在再入返回段使用,大部分飞行任务阶段是“死重”,为返回舱质量控制带来相当的难度。

综上,从质量系数、再入控制难度、工程研制经验等方面考虑,带翼升力体外形的返回舱不适宜执行载人深空探测任务。

对钝头体和双圆锥体在过载方向、气动稳定性两方面进一步深入分析。

1)过载方向

再入过程中,气动力对于钝头体主要产生轴向过载,如图6所示,主要的减速也来自轴向。这与发射时的最大过载方向一致,即发射、逃逸、返回时返回舱最大过载方向一致。相反,对于细长体而言,产生的主要过载方向垂直于轴线方向。这个过载方向与发射时的最大过载方向相差90°。这些过载方向将影响航天员的座椅方向。对于返回舱而言,航天员的背部平行于防热大底,所有主要过载均从航天员背部穿入胸部穿出,此方向是人类所能承受最大过载的方向。而对于双圆锥体而言,主要过载方向在发射和再入时相差90°(如图6所示)。因此,或者使航天员的座椅可以在飞行中旋转调整,或者设计出较小的发射过载使航天员有所适应,设计难度增大。

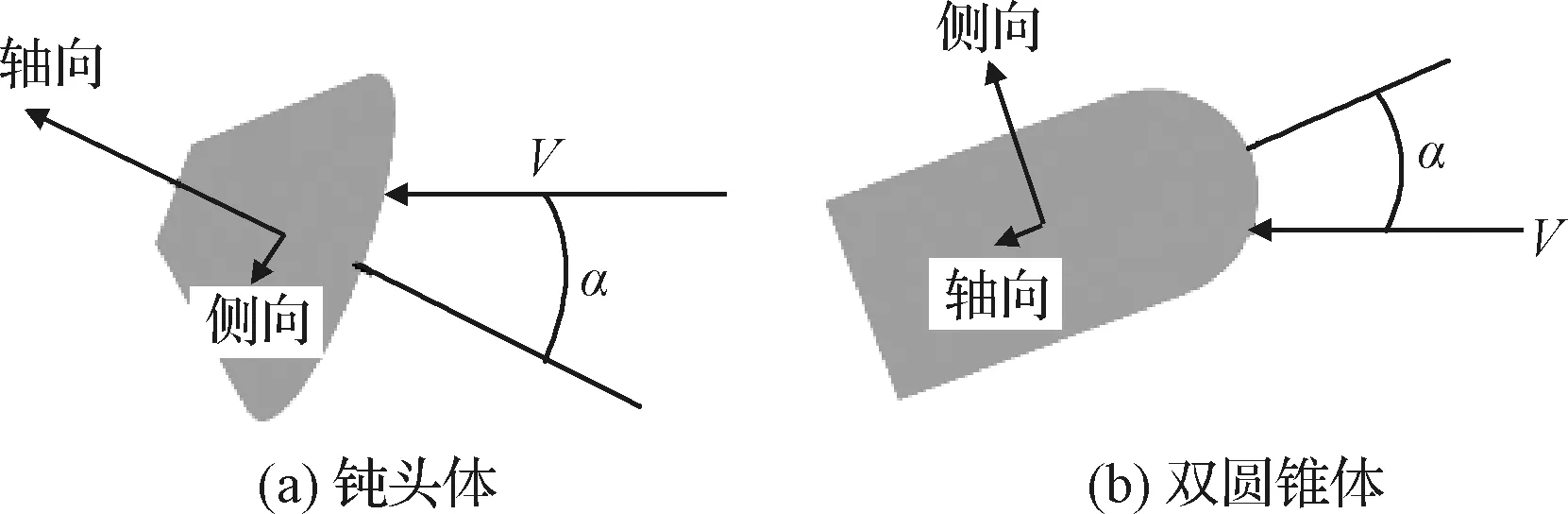
图6 返回舱再入过程过载方向分布Fig.6 Overload direction distribution of reentry capsule during reentry

2)气动稳定性

在钝头体与双圆锥体气动稳定性对比过程中,以阿波罗气动外形作为钝头体典型案例进行分析,双圆锥体选择的是类CTV(乘员转移飞行器)外形。为了应付再入过程中的各种可能情况以及提高返回舱安全可靠性,为返回舱设计一个被动的气动稳定构型是十分必要的。

图7给出了钝头体返回舱再入过程中的坐标系定义,其中大头朝前为零攻角状态。图8给出了阿波罗和类CTV两种外形的俯仰力矩随攻角变化范围及相对应的质心位置,其中大头朝前为零攻角状态。红色曲线为满足单点稳定的俯仰力矩—攻角曲线,对应的返回舱质心位置以红点形式标出。

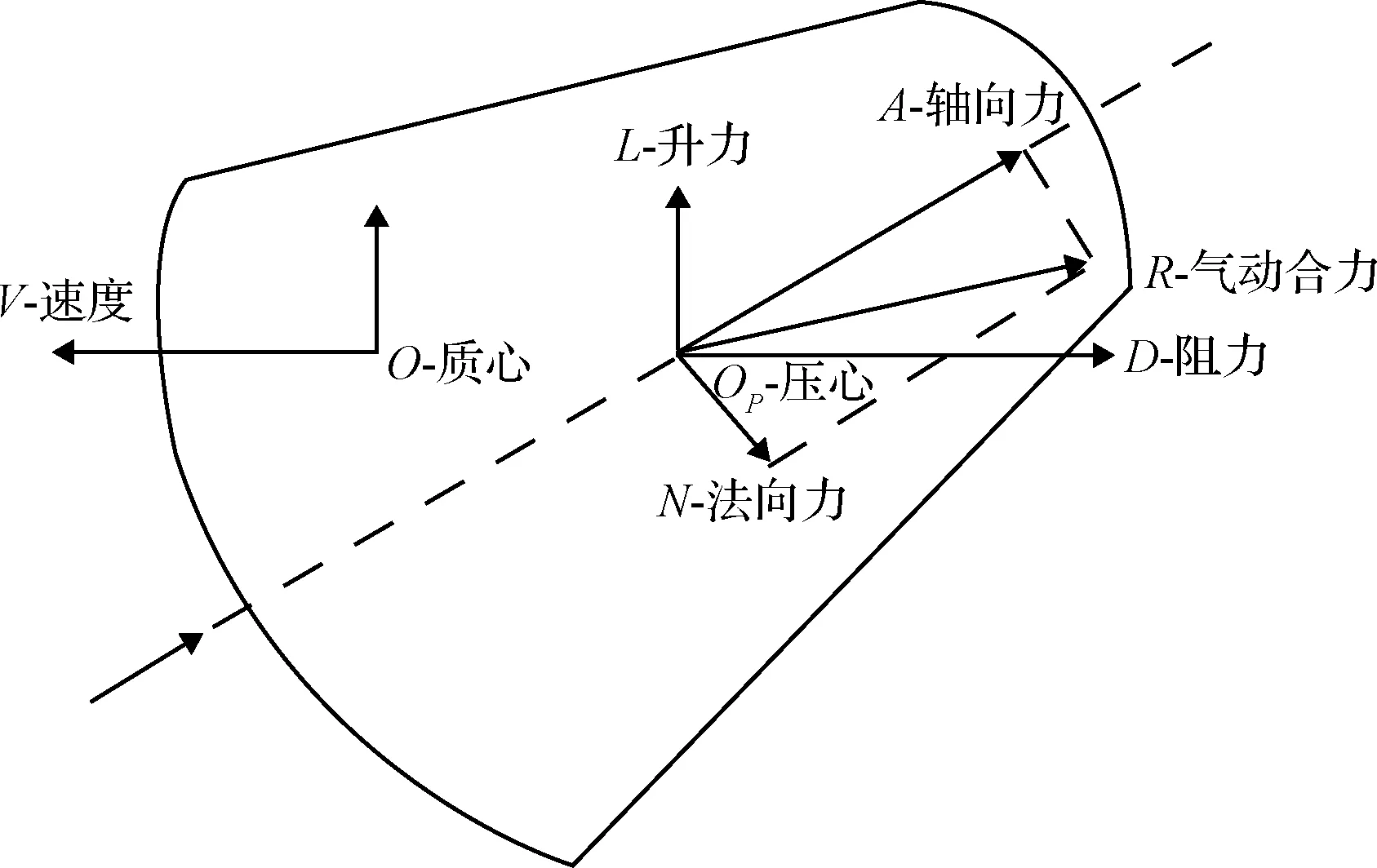
图7 返回舱再入坐标系Fig.7 Reentry coordinate system of the reentry capsule

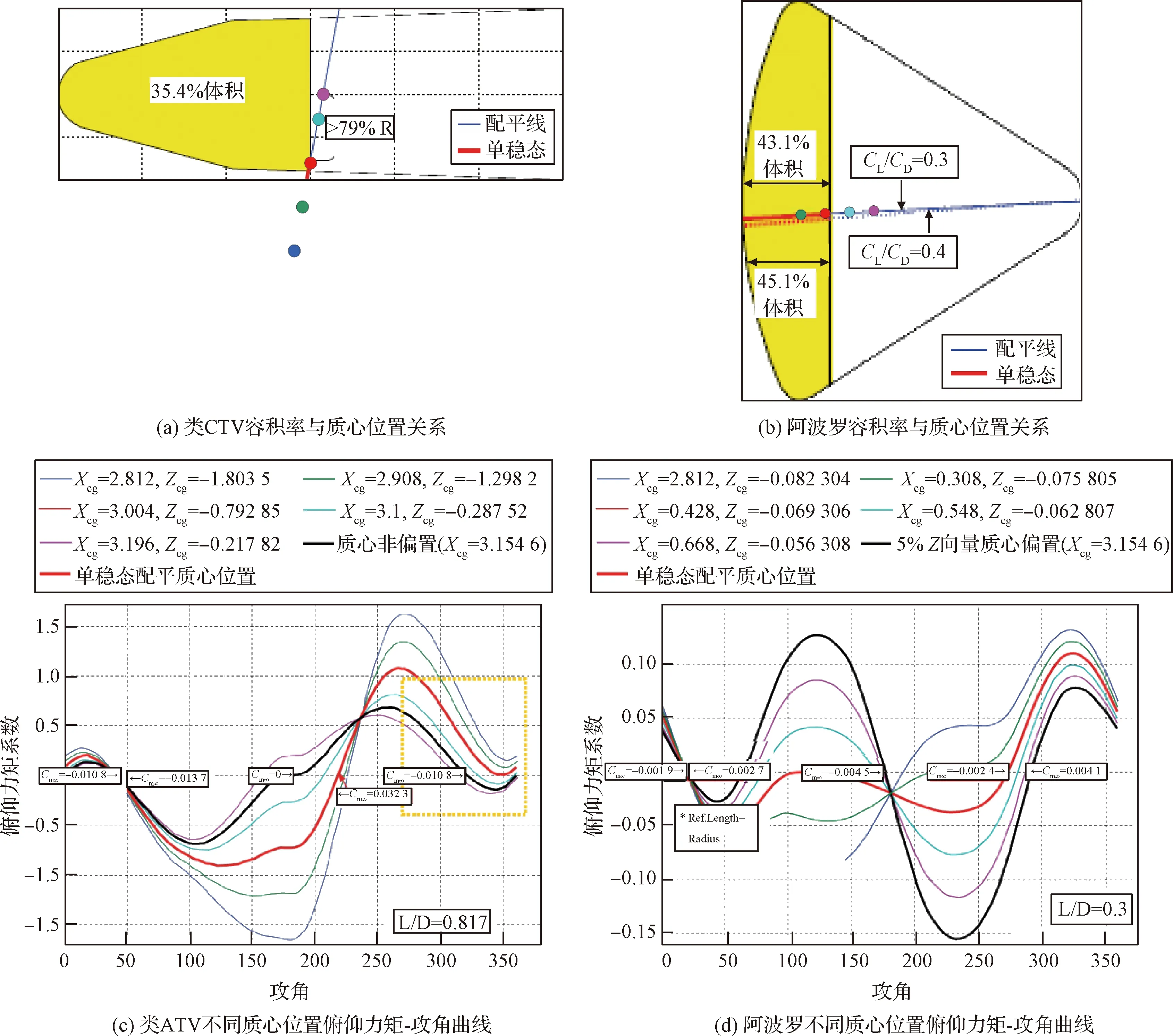
图8 返回舱质心位置及俯仰力矩-攻角曲线[21]Fig.8 Curves of locations of the center of mass and pitching moment versus angle of attack of the reentry capsule[21]

从图8中可以看出:阿波罗外形的质心位置配平线和中心线很接近,满足单点稳定性要求的质心位置和相对体积是可以达到的,具有更好的单点稳定特性。对于细长体,质心位置需在红点以下才可以满足单点稳定性要求,很显然,这样的质心位置是难以实现的。

综上分析,国外在研的新飞船仍以钝头体外形为主,由此也可以看出,从再入航天器气动外形选形来看,仍然以钝头体外形作为主要研究方向[19-20]。

3 气动外形优化方法

气动外形分析是一个复杂而耗时的过程,而优化往往是成千上万次迭代的过程,直接使用气动外形分析来做优化将非常耗时。

基于代理模型的优化算法(SBO)由于能够实现高效全局优化,逐渐成为了气动优化设计领域的研究热点之一。目前常用的气动优化设计方法主要包括梯度优化方法和启发式优化方法两大类[22]。针对气动优化设计的多极值特性问题,算法选择具有重要影响,需要进一步提高代理优化算法的全局搜索能力[23-24]。或者结合总体需求对于多极值设计给予更多限定条件或判定准则。

针对钝头体返回舱气动选形,可以采用在设计空间中选取样本点并分析,根据样本分析数据建立近似模型,然后利用近似模型进行优化。国内大多是应用内伏牛顿理论及定常势流格林函数法计算飞行器气动性能,通过遗传算法来优化设计新外形的气动布局。本文主要基于Isight的方法,结合基于内伏牛顿理论的气动力工程估算和基于弹道的热流估算结果,根据工程需要确定了相关优化目标,进而确定不同优化外形。

3.1 样本空间选取原则

样本点选取采用最优拉丁超立方(optimal Latin hypercube)试验设计方法。这是一种从多元参数分布中近似随机抽样的方法,属于分层抽样技术,常用于计算机实验或蒙特卡洛积分等。

该方法对所有的因子取相同水平均匀分布,组合各个水平来指定点数,保证每个水平都被包含一次,通过优化拉丁超立方矩阵,使得采样点在设计空间均匀分布。随机拉丁超立方方法和最优拉丁超立方方法如图9所示。

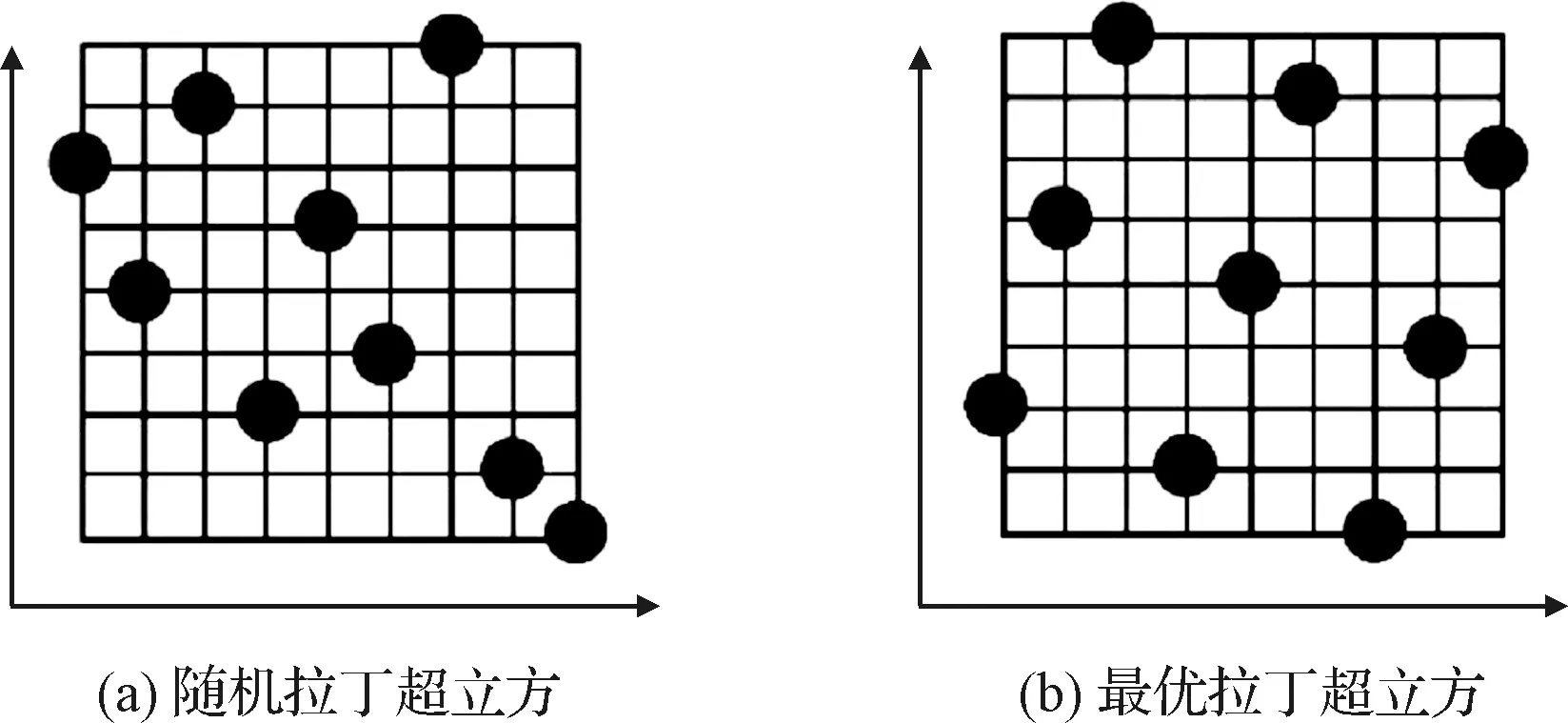
图9 拉丁超立方试验设计实例Fig.9 Examples of design of Latin hypercube experiments

本文主要针对肩部倒角半径Rc、球冠半径Rn、倒锥角θ这3个主要气动外形参数建立样本空间,并在Isight中通过最优拉丁超立方选取的样本点输入参数给出样本。

3.2 气动力工程估算

3.2.1工程估算方法介绍

在气动力计算中,为了快速完成计算子样的气动力计算,确定采用基于内伏牛顿理论的工程估算方法代替原有的数值模拟。当钝头体返回舱的外形参数大底球冠半径Rn、倒锥角θ、肩部倒角半径Rc、长细比λ和最大横截面直径dm等选定后,根据几何关系可推导出外形母线方程和各特征点参数,以此计算气动性能。

为方便计算,将返回舱分为3个区域:Ⅰ区为大头球冠区(0～x1),Ⅱ区为肩部圆倒角区(x1～x3),Ⅲ区为倒锥角区(x3～x4),如图10所示。

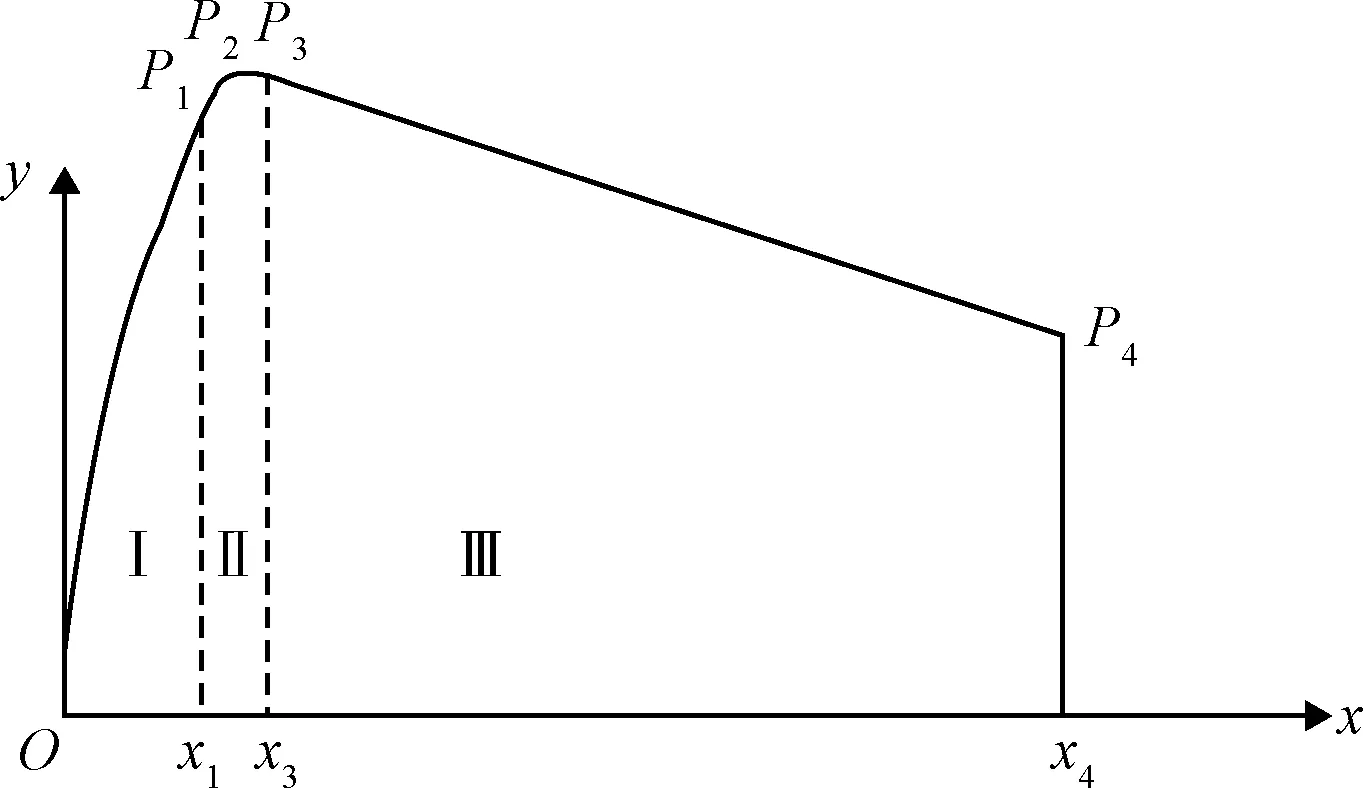
图10 返回舱工程估算区域范围Fig.10 Reentry capsule engineering estimation range

表2给出了3个区域内的几何参数、特征点参数、母线方程等。

表2 返回舱外形与特征点计算公式Table 2 Calculation formula of the shape and characteristic points of the reentry capsule

迎风面元压力系数Cp,w为

Cp,w=Cp0cos2η,cosη>0

(1)

背风阴影区的压力系数Cp,1为

Cp1=0,cosη≤0

(2)

式中:η为面元外法向n与自由流速V∞的夹角。

cosη=(V∞·n)/(|V∞||n|)=

cosα·cosθ+sinα·sinθ·cosφ

(3)

式中:α为攻角;θ为面元法向与体轴的夹角;φ为子午角。

驻点压力系数Cp0为

(4)

轴向力系数CA、法向力系数CN及俯仰力矩系数Cm0的计算公式分别为

(5)

(6)

(7)

式中:τ为面元切线与体轴的夹角,tanτ=dr/dx可由表2中列出的切线方程计算[25]。

3.2.2典型算例验证对比

为了验证工程估算的真实性,本文利用数值模拟方法对工程估算结果进行了检验。利用网格划分软件ICEM完成了三维建模,并使用计算流体力学软件Fastran进行求解。由于要考察单稳态配平特性,计算工况要覆盖返回舱[0°,-180°]区域,在进行网格建模时采用3套网格,分别计算[-65°,-15°]、[-125°,-70°]和[-180°,-130°]。计算时物面等温壁Tw=5T∞,大气模型采用1976美国标准模型。图11、图12给出了数值计算网格模型和部分工况的云图显示。

图11 小攻角附近网格及25°攻角压力云图Fig.11 Grid near low angle of attack and pressure cloud map at 25° angle of attack

图12 大攻角附近网格及90°攻角压力云图Fig.12 Grid near high angle of attack and pressure cloud map at 90° angle of attack

工程估算结果与数值模拟计算结果的对比情况如图13所示。可以看出两者的升阻比和俯仰力矩曲线基本相同,仅在大攻角(90°～180°)情况下差距相对较大,但基本趋势相同,因此可以利用工程估算结果开展定性分析。

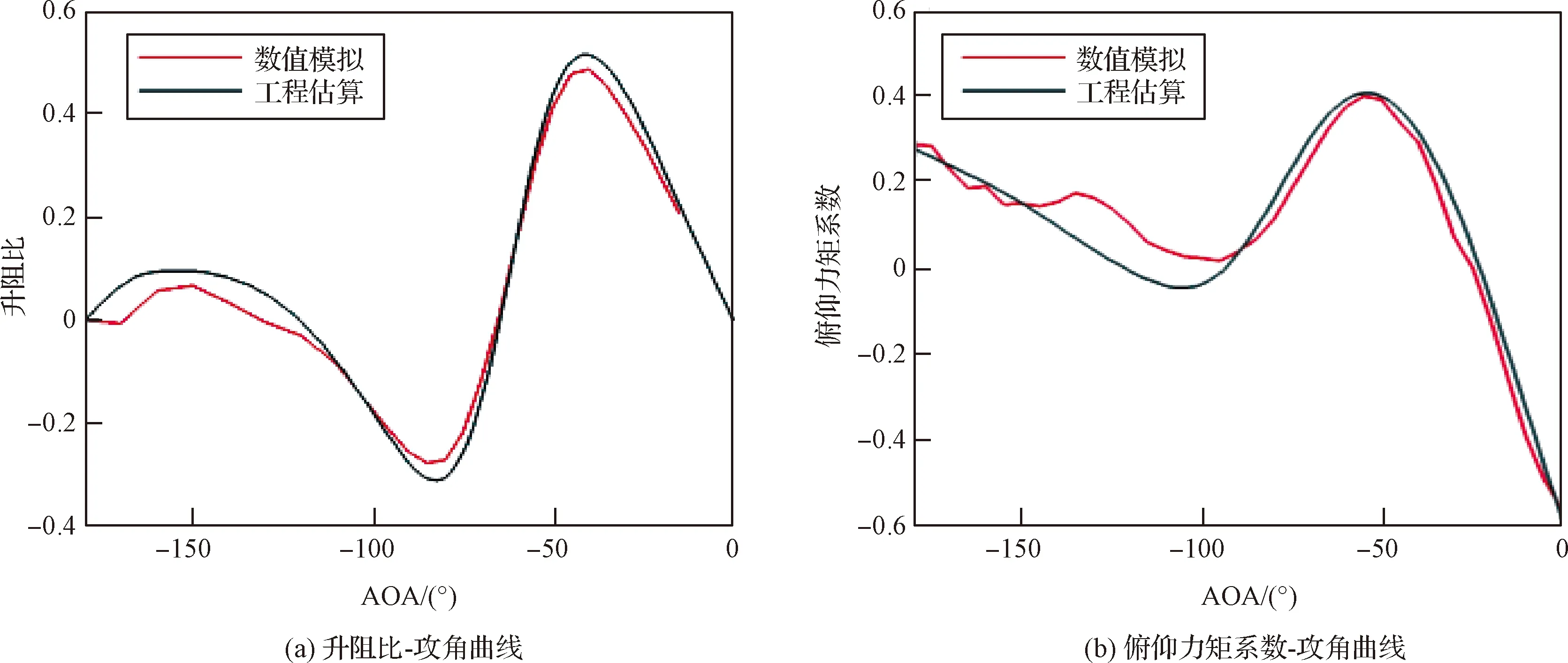
图13 工程估算结果与数值模拟结果对比Fig.13 Comparison between engineering estimation results and numerical simulation results

本文提到的工程估算方法,针对钝头体轴对称返回舱,利用Matlab完成一个马赫数全攻角计算用时2～3 s;若采用传统数值模拟,考虑500w网格并行计算,需要6 h左右完成收敛。因此对于前期气动外形设计阶段,需要对多个外形尺寸对比分析,采用工程估算方法可以大幅提升计算效率。

3.3 弹道及热流工程估算

3.3.1弹道计算模型

再入返回过程中的高度、速度、当地水平速度倾角等弹道参数是气动力、热分析与设计的直接输入。因此,在开展气动外形优化设计过程中,必须融合弹道计算以实现对设计结果的定量评估。本文在气动外形优化设计中采用的弹道计算模型主要包括弹道计算动力学模型和制导算法两方面。

其中,再入动力学方程可以建立在半速度坐标系下,形式如下:

(8)

式中:r为飞行器地心距;V为飞行器相对大气的速度(不考虑风的影响);ε为飞行器经度;φ为飞行器地心纬度;γ为再入倾角;Ψ为再入航向角;L为飞行器升力;D为飞行器阻力;Ω为地球自转速度;σ为倾侧角。

本文利用传统设计方法给出标称弹道,并据此开展后续热环境估算。

3.3.2热流工程估算模型

返回舱高速再入过程中的气动加热程度通常以驻点位置热流密度的形式来描述。驻点热流工程算法有多种,其中较常用的驻点公式有Fay-Riddell,Kemp-Riddell,修正Kemp-Riddell,Lees,修正Lees等。对返回舱而言,多采用Kemp-Riddell公式或修正Kemp-Riddell公式。

Kemp-Riddell公式由Fay-Riddell驻点热流公式发展而来,Fay-Riddell公式根据轴对称体高速边界层基本方程,利用相似求解给出。Kemp-Riddell公式通过对实际卫星再入大气层轨道进行大量计算,并用来流条件和几何参数进行数据相关性分析,得到与Fay-Riddell公式相差不超过5%的计算公式。此后,通过Rose-stark激波管实验,获得了精度更高的修正Kemp-Riddell公式。

本文再入返回中的热流工程估算采用成熟的修正Kemp-Riddell公式,即

(9)

式中:Rn为驻点曲率半径;v∞为再入速度;ρ∞为再入返回过程中不同速度v∞对应的大气密度;ρ0=1.225 kg/m3,vc=7 925 m/s。

4 气动外形优化

4.1 建立近似模型

4.1.1优化目标选择

优化目标最终选择升阻比(CL/CD)、有效容积率和最大热流作为多目标优化条件。3种条件定位及来源如下:

根据前期经验,对于第二宇宙速度再入而言,为保证落点精度,一般要求升阻比大于0.3。而根据典型外形的气动力工程结果(如图8所示),初步按照25°作为配平攻角时的升阻比作为样本选取;最大热流通过弹道及热流工程估算算法计算得到。

4.1.2样本数据汇总

有效容积率为气动力工程估算后,在确定该外形可实现单稳态配平的最低质心位置做一垂直于返回舱轴线的平面,平面以下(靠近大底区域)为有效容积(如图14所示),有效容积率即为有效容积占整个返回舱体积的比率。

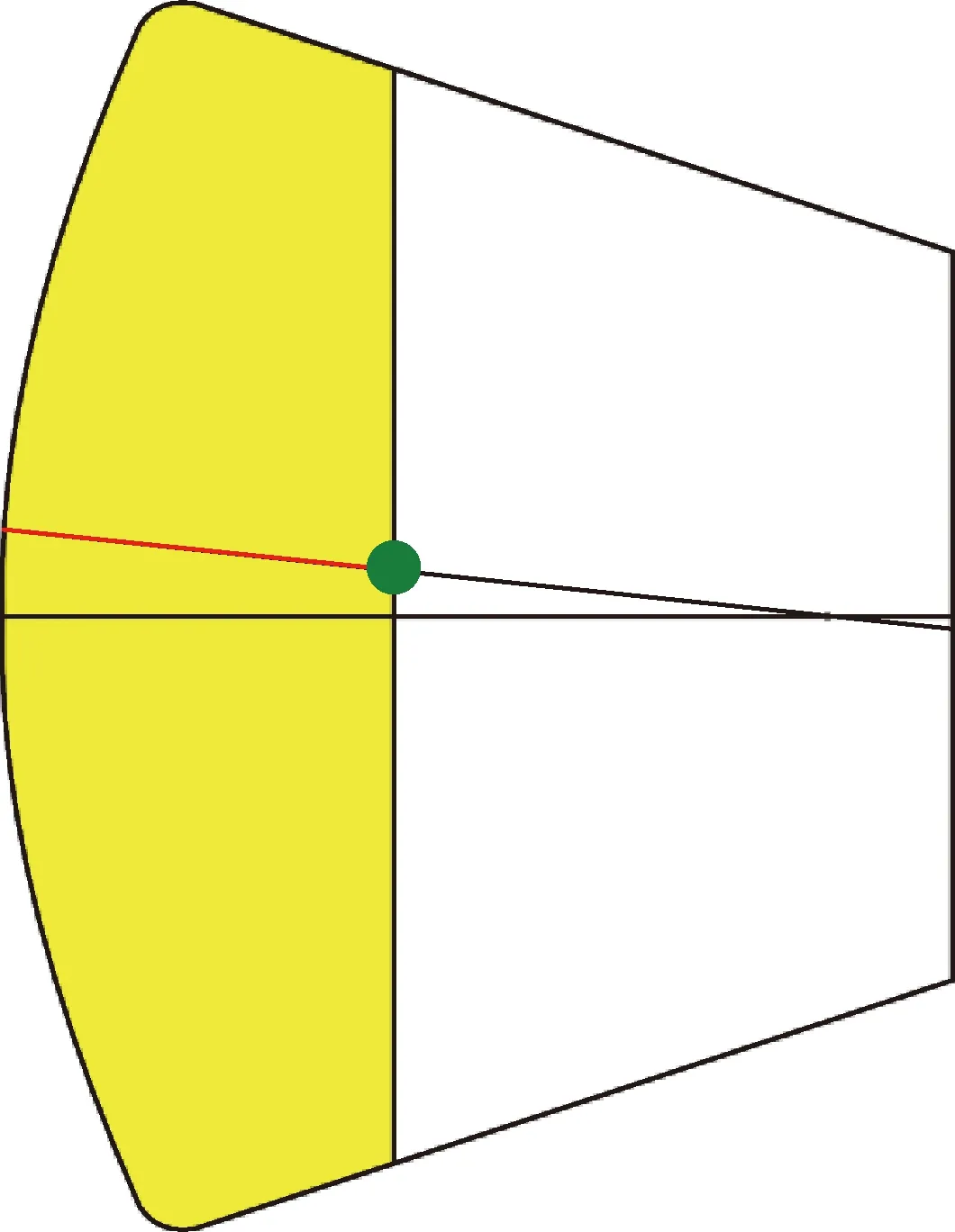
图14 返回舱有效容积Fig.14 Effective volume of the reentry capsule

样本数据汇总结果如表3所示。选择肩部倒角半径(Rc)、大底球冠半径(Rn)、倒锥角(θ)作为多目标优化输入条件,将升阻比(CL/CD)、容积率和最大热流作为多目标优化输出条件。后续将根据该样本数据进行优化选择。

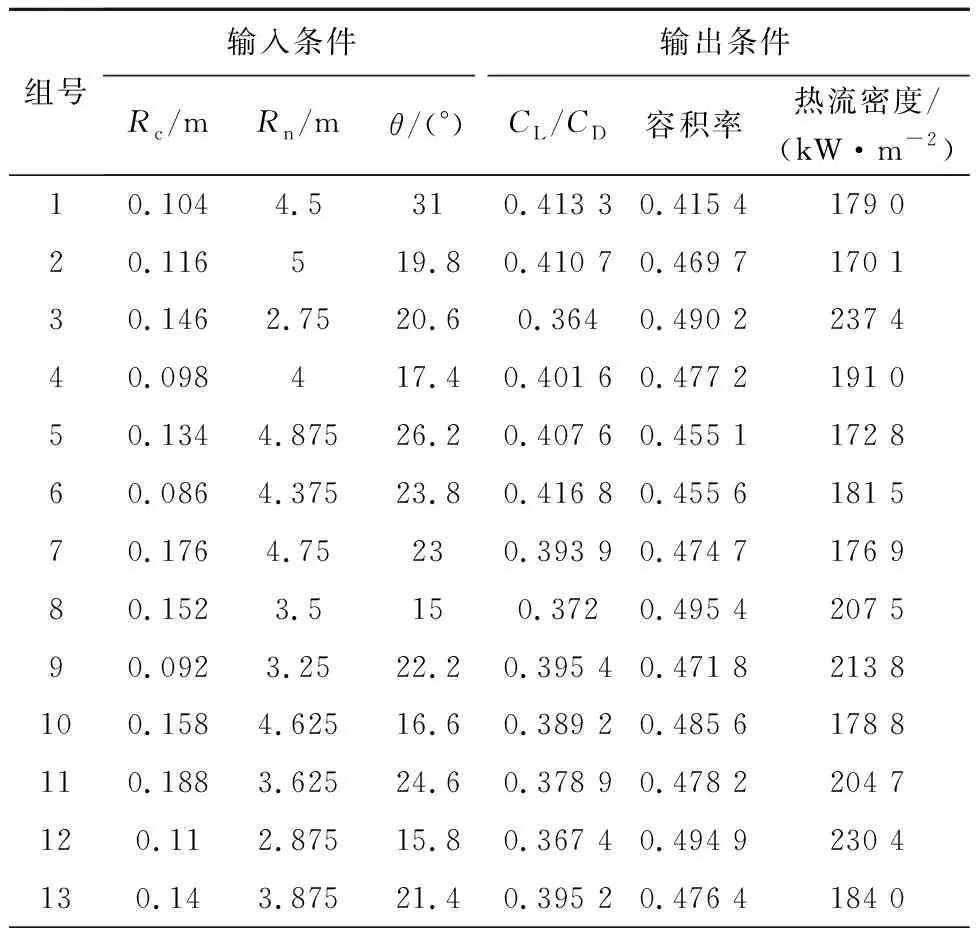
表3 样本数据汇总Table 3 Sample data summary

利用表3中的数据采用响应面(response surface)法建立气动分析的近似模型,模型各项系数如表4所示。

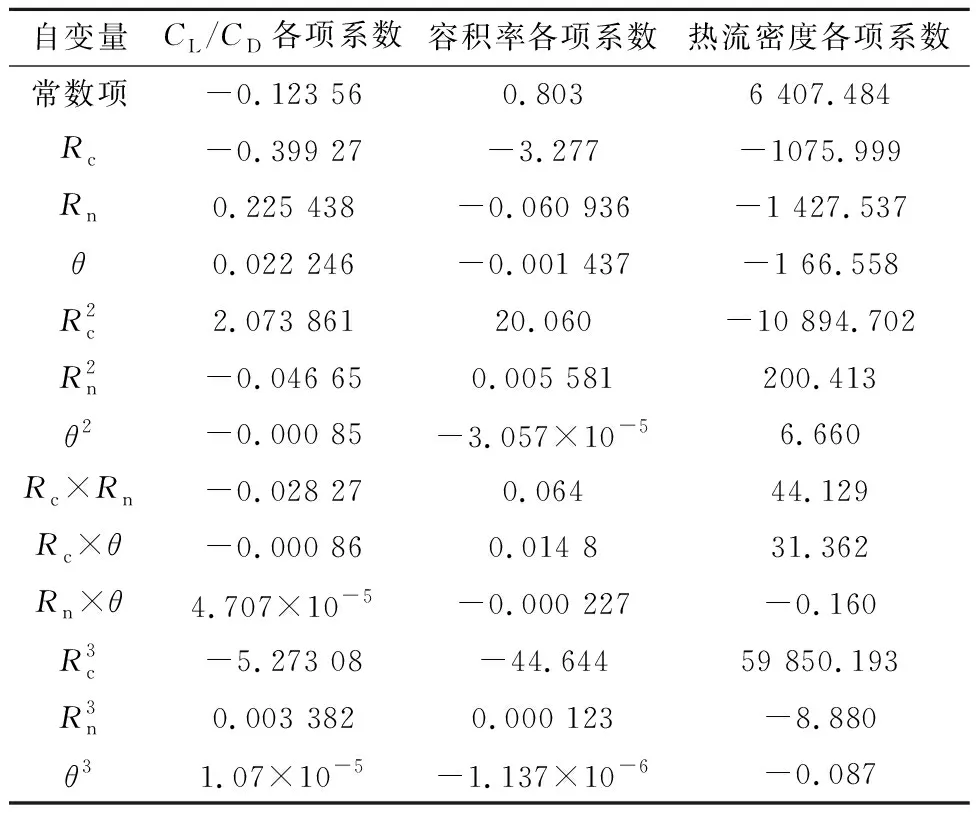
表4 气动分析的响应面近似模型系数Table 4 Response surface approximation model coefficients for aerodynamic analysis

4.2 近似模型校核

为确定近似模型是否可以正确反映原问题,采用另外计算的两组数据对近似模型进行复核。首先,用两组数据分别进行仿真分析和近似函数计算,然后对结果进行对比,对比结果如表5所示。

表5 近似模型校核结果Table 5 Verification results of the approximate model

由表5中的对比可见,近似模型计算结果与仿真分析计算结果基本吻合,说明近似模型具有较高的可信度,可用于进一步优化计算。

4.3 基于近似模型的气动外形优化

设计变量为气动外形参数,具体为表2中的输入条件。其定义的取值范围如下:肩部倒角半径Rc∈(0.08, 0.2) m、球冠半径Rn∈(2.5, 5) m、倒锥角θ∈(15°, 31°)。

4.3.1单目标优化

分别以升阻比(CL/CD)最大化、容积率最大化、热流最小化为目标,除设计变量上下界外不加约束条件,选择序列二次规划算法NLPQL,优化结果如表6所示。

表6 单目标优化时的优化结果Table 6 Results of single-objective optimization

4.3.2双目标优化

对于新一代载人飞船而言,容积率和峰值热流为重点关注对象,升阻比可作为约束条件。在此基础上以容积率最大化和热流最小化为目标,约束升阻比大于0.36,选择NSGA-II多目标优化算法,设置容积率和热流的比例因子分别为0.5和1 700,使得两个目标数值在同一水平上,迭代求解后,优化结果如表7所示。

表7 双目标优化时的优化结果Table 7 Results of dual-objective optimization

升阻比、容积率、热流的临界的可行解迭代过程如图15所示,迭代过程的散点图如图16所示,其中蓝色的点为帕累托前沿,红色的点为不可行解。

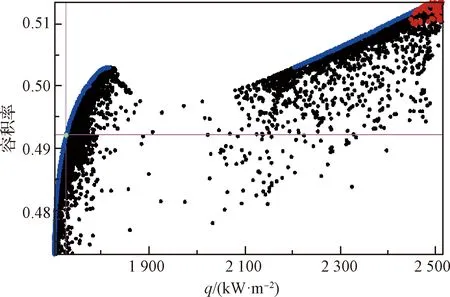
图16 两个优化目标的散点图(蓝色点为帕累托前沿)Fig.16 Scatter plots of the two optimization objectives (blue dots represent Pareto frontiers)

4.4 小 结

本节给出了通过建立近似模型开展外形优化的初步算例。其主要目的为尽快优化出满足总体目标需求的最优外形。参考本节样本数据参数共包含21个样本,若采用传统计算模式,需要考虑倒锥角、球冠半径以及肩部倒角半径3个变量进行遍历,假设每个变量选取10个点,需要完成1 000个样本计算后再对比分析。因此采用近似模型的办法可以将优化效率提升近两个量级。

5 飞行验证与评估

5.1 多用途飞船缩比返回舱飞行验证

新一代载人飞船返回舱采用本文设计方法优化后的气动外形,搭载CZ-7运载火箭首飞开展飞行试验,于北京时间2016年6月25日发射,6月26日下午安全着陆于东风着陆场巴丹吉林沙漠预定落区,获取的气动数据完整有效,飞行任务取得圆满成功,如图17所示。

图17 返回舱成功返回地面Fig.17 Reentry capsule successfully returned to the Earth

本次试验以验证气动外形为主要目的,采用近地半弹道式再入返回。为获取真实有效气动数据,再入过程中并未进行姿态控制,从而获取了更为准确的气动数据。

着陆后对防热烧蚀情况进行检查,见图18、19。从烧蚀流线图分析,烧蚀结果与仿真预示基本一致。基本验证了飞船实际再入过程中的攻角与前期设计相匹配。

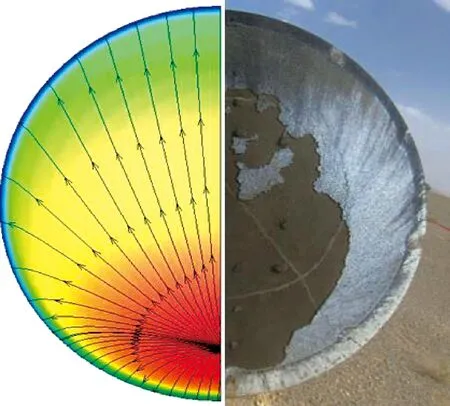
图19 大底烧蚀形貌检查Fig.19 Inspection of bottom ablation morphology

5.2 新一代载人飞船试验船飞行验证

新一代载人飞船试验船返回舱同样采用本文优化厚度气动外形,搭载CZ-5B火箭开展飞行验证试验,对新一代载人飞船的高速再入返回控制、热防护、群伞回收等关键技术进行飞行验证。

试验船2020年5月5日在海南发射场成功发射,5月8日安全返回巴丹吉林沙漠预定落区,任务取得圆满成功,如图20所示。通过本次飞行试验对新一代载人飞船返回舱气动外形高速再入返回的适应性进行了验证,获取了大再入角下的高精度再入气动力数据,结果表明该外形可应用于后续深空探测任务的再入返回。

图20 试验船返回舱成功返回地面Fig.20 Testing version of the reentry capsule successfully returned to the Earth

5.3 气动外形评估

本节主要针对多用途飞船缩比返回舱飞行验证数据进行处理。重点针对优化后的气动外形的数据准确性进行验证。

5.3.1配平攻角评估

如图21所示,飞行全程攻角变化与仿真结果基本一致,再入期间在-25°配平攻角附近震荡收敛,说明返回舱具有良好的单稳配平特性,满足“高超声速全攻角范围内具有唯一稳定配平点”的设计要求。

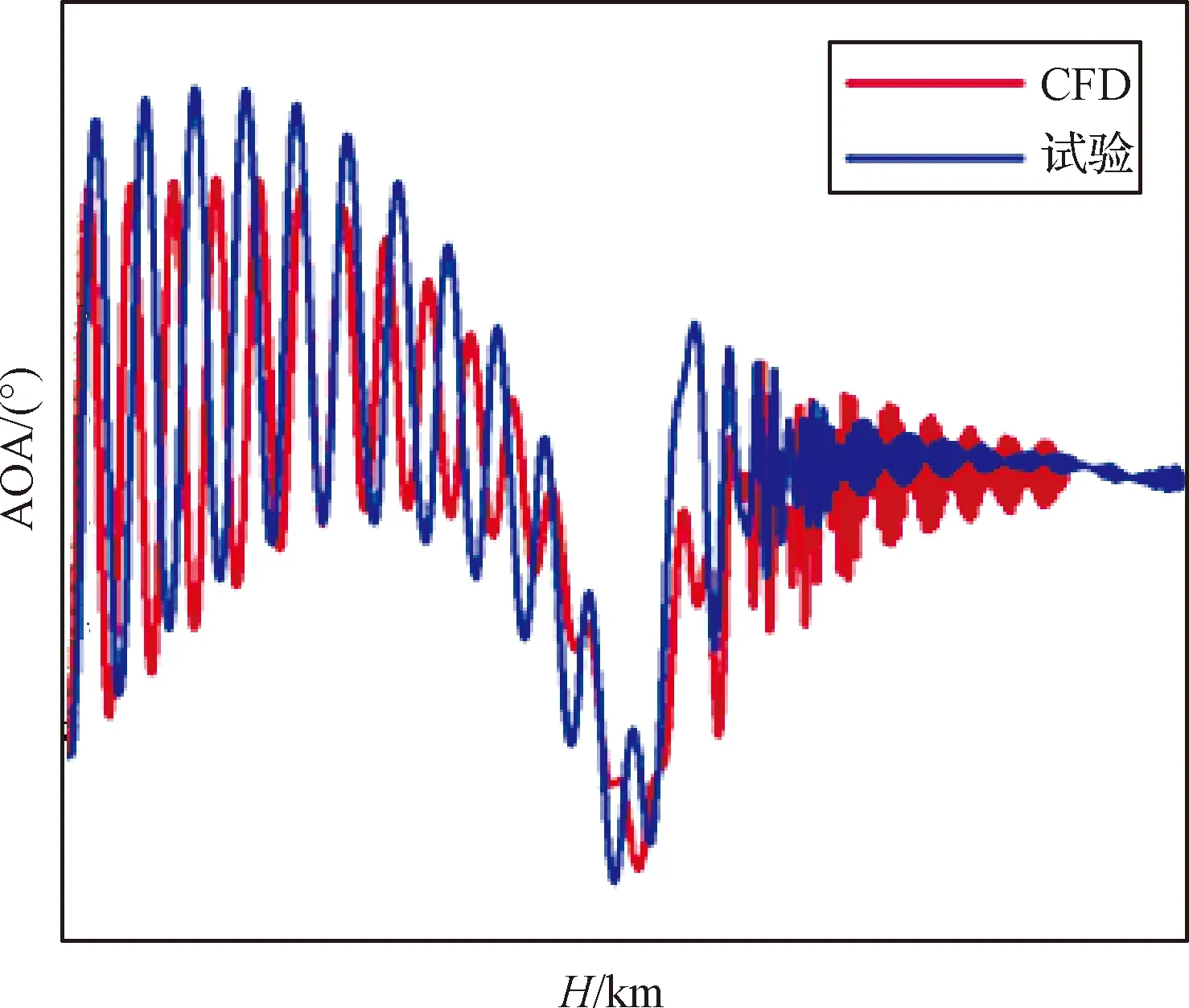
图21 攻角-高度变化曲线Fig.21 Curves of angle of attack versus height

5.3.2升阻比评估

图22、图23利用大底布置的FADS系统,结合内侧弹道,可解算出真实飞行状态下的气动力数据。同时解算出的气动力数据偏差主要由以下三方面组成:1)FADS系统中气动压力传感器测量误差;2)FADS系统辨识偏差;3)记录内侧弹道的加速度计、陀螺测量偏差。

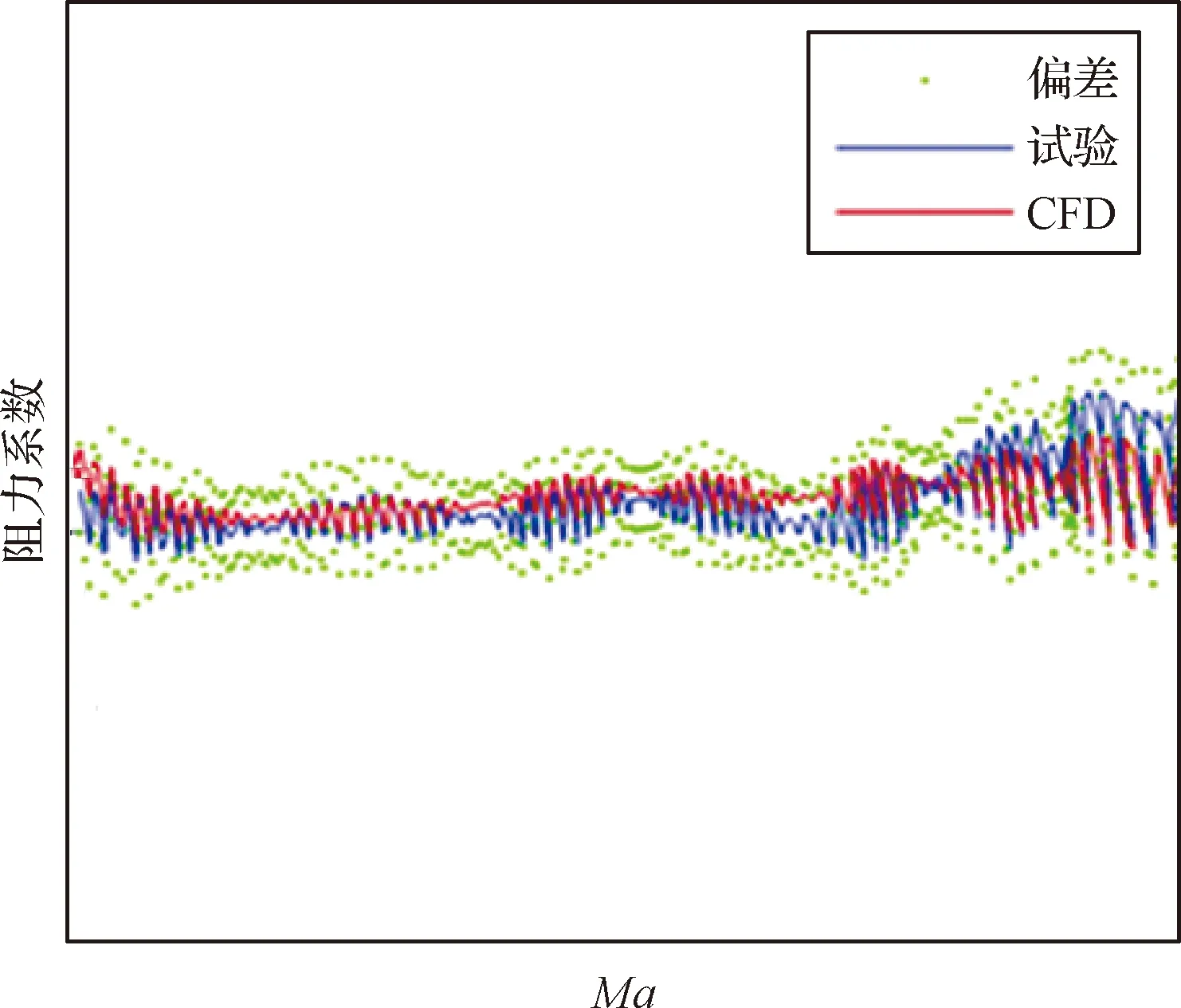
图22 阻力系数-马赫数变化曲线Fig.22 Curves of drag coefficient versus Mach number

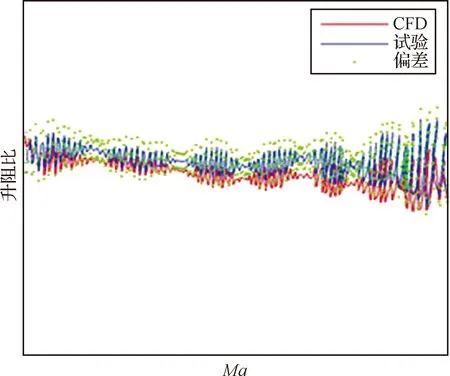
图23 升阻比-马赫数变化曲线Fig.23 Curves of lift-to-drag ratio versus Mach number

根据70 km以下气动力系数辨识结果来看,阻力系数以及升阻比仿真结果基本一致,且仿真结果在飞行试验的气动力系数偏差范围内,表明仿真结果的正确性。

综上,通过对多用途飞船缩比返回舱的在轨真实气动力数据处理及评估,其配平攻角、阻力系数、升阻比等指标与预估一致。达到预期设计要求,进一步验证了使用本文优化方法设计的新一代载人飞船返回舱气动外形的各项气动性能指标满足设计要求。

6 结束语

本文以新一代载人飞船需要具备第二宇宙速度再入返回能力为目标,在完成基本外形初选后,提出了一种快速的气动外形优化设计方法。该方法从Isight多目标优化角度出发,结合基于内伏牛顿理论的气动力工程估算和基于弹道的热流估算结果,分别进行单目标优化和多目标优化。利用该方法完成了新一代载人飞船返回舱的气动外形优化设计,并通过飞行试验结果得以验证。