登月火箭剩余运载能力估计与停泊轨道重规划

王 聪，王劲博，宋征宇

(1. 北京航天自动控制研究所，北京 100854；2. 中山大学系统科学与工程学院，广州 510275；3. 中国运载火箭技术研究院，北京 100076)

0 引 言

载人登月任务的第一步是利用运载火箭将载人飞船送入地月转移轨道,火箭2 000余秒的飞行时间相较于地月转移轨道约120小时的飞行时间,占比小于0.5%,却为飞船提供了95%以上的能量,因此,运载火箭的飞行控制精度和可靠性是载人飞船进入环月轨道的重要前提。相比于无人月球探测任务,航天员的安全性要求尤为突出,从运载火箭制导控制的角度,在非致命故障下合理利用剩余运载能力,对火箭飞行轨迹进行重规划,将载人飞船安全送入停泊轨道等待救援或自主返回,是载人登月火箭不可或缺的能力。

当动力系统出现轻微故障时(如推力微小幅度下降)[1],火箭仍可继续采用迭代制导、动力显式制导[2]等经典闭环制导方法进入目标轨道。然而,如果故障程度较大以至于目标轨道不可达,则传统制导方法无法适用。在这种情况下,新的自主制导方法需要充分利用火箭剩余能量,将载荷送入较低或不同轨道面的救援轨道,这就涉及到运载火箭故障后的在线运载能力评估与任务、轨迹重构。

美国SLS Block-1B火箭采用了离线仿真装订和在线查表评估的方式来提高其非致命故障条件下的鲁棒性[3]。然而,这种方法仅适用于有限的故障模式,且在复杂故障条件下,在有限数据库中查表拟合的重构轨迹势必不是最优的,甚至是不可行的。近年来,在计算制导与控制(Computational guidance and control, CG&C)新范式的牵引下[4],众多学者提出,采用在线重构优化的方式同时确定火箭剩余运载能力、降级轨道和后续制导策略。Song等[5-6]针对卫星发射任务,提出了基于状态触发(State trigge-red indices, STI)的在线轨迹优化方法,用以解耦轨道根数带来的复杂终端约束并提高计算效率。通过求解一系列保真度和复杂度越来越高的子问题,可同时得到与目标轨道最接近的降级救援轨道根数以及对应的后续飞行轨迹。结合基于迭代制导的剩余能力评估以及STI方法,Song等[7-8]进一步构造了较为完整的运载火箭自主任务重构策略,尽可能将载荷送入原目标轨道。考虑大气层内的上升段飞行,Ma等[9]基于改进的Chebyshev-Picard迭代方法和投影牛顿法,提出了一种高效的制导方法来应对火箭推力下降故障,可同时给出降级停泊轨道和对应的制导指令。利用神经网络强大的非线性拟合能力,何骁等[10]提出了一种离线训练、在线拟合的轻量化重构方法,一方面可直接用于入轨能力评估和在线任务重构,另一方面其计算结果可用于热启动在线轨迹优化算法[11]。不同于单飞行段易于在线数值求解,Wang等[12]提出了跨滑行段的动力-滑行-动力制导重构方法,通过简化问题,仅采用牛顿迭代即可快速收敛到可行解,对发射太阳同步轨道载荷具有较好的效果。

基于凸优化的方法是在线轨迹优化研究领域的一个重要分支,得益于底层计算快速、可靠的收敛特性,凸优化方法在近年来被广泛应用于运载火箭上升段、飞行器再入、火箭着陆、空间交会对接等问题的轨迹规划与在线制导[13-14]。对于运载火箭任务及轨迹重构问题,Hao等[15]提出一种迭代二阶锥规划算法来生成半长轴最大的救援轨道,其设计了两层迭代策略,外层迭代用于搜索救援轨道的入轨点纬度辐角,使得内层迭代中终端约束的非线性程度得以下降,进而可采用内点法高效求解。Li等[16]提出了结合无损凸化和序列凸化的火箭在线轨迹重构方法,并针对不同推力故障下降程度建立了对应的性能指标和终端约束模型,以提高在线计算效率。Miao等[17]提出引入虚拟控制来补偿火箭推力故障下降造成的加速度损失,并采用凸优化方法确定火箭在当前故障条件下能否进入目标轨道。

现有研究多针对卫星发射任务,讨论如何在故障下尽可能将载荷送入原目标轨道,或在能力不足时,将载荷送入最接近原目标轨道的救援轨道,再通过载荷消耗燃料和寿命的方式变轨,从而完成原定任务。然而,该设计思想并不适合载人登月火箭,若在较严重故障下将载人飞船送入远地点、轨道倾角或近地点幅角不满足入轨精度要求的救援轨道,则载人飞船将无法通过轨道中途修正进入月球引力影响球;同时,大椭圆救援轨道周期长,航天员将被迫飞向几万甚至十几万千米外的远地点,风险更大。更适合的救援方式是在快速评估剩余运载能力不能进入原目标轨道后,通过重规划控制火箭进入近地停泊轨道,既便于地面监测,也满足载人飞船自主返回的初始状态。

本文针对推力下降故障,研究了基于剩余运载能力估计的登月火箭停泊轨道重规划方法,解决剩余运载能力的准确快速评估和飞行轨迹可靠在线重规划的难题。第1节描述运载火箭从起飞到入轨的全过程运动模型和约束条件;第2节结合地月转移轨道特点和火箭构型,介绍剩余运载能力估计方法;第3节提出基于状态触发的停泊轨道重规划方法,并给出了基于地心角估计的初始猜想凸优化方法;第4节设计了上升段全程飞行轨迹,并通过数值仿真分析了推力下降故障下的剩余运载能力和轨迹重规划结果;第5节总结全文。

1 运载火箭上升段问题描述

本节以典型的三级半构型运载火箭为对象,针对起飞到入轨全飞行剖面的特点,分析助推、一级、二级、三级一次、滑行和三级二次飞行段的初始状态、终端状态和过程约束条件,并给出相应的数学表达。

1.1 上升段飞行剖面分析

1)助推飞行段

首先考虑出塔安全,需要先垂直上升飞行,在确保出塔的情况下,定时进入程序转弯飞行。考虑火箭在大气层内飞行,除推力外,需要考虑气动力对箭体的作用,同时考虑飞行过程中的弯矩约束条件,避免由于载荷过大导致结构受损,从而实现对程序转弯过程角速度变化率的约束。

2)一级飞行段

芯一级飞行段运动方程约束、飞行过程中的弯矩约束与助推段一致。本飞行段初始时间和速度位置与助推段终端一致,初始质量为助推段终端质量抛掉助推器后的剩余质量。

3)二级飞行段

考虑运载火箭在芯二级飞行段将飞出大气层,可忽略气动力对箭体运动的作用,并具备抛掉整流罩的条件,不需要考虑弯矩约束,采用传统的相对定时抛罩策略对抛罩时间进行约束。本飞行段初始时间和速度、位置与芯一级飞行段终端一致,相应的初始质量为芯二级火箭的总质量。

4)三级一次飞行段

考虑载人登月任务对航天员安全性的要求,三级一次飞行段的终端条件需满足停泊轨道要求。本飞行段初始时间和速度、位置与芯二级飞行段终端一致,初始质量为三级火箭的总质量。

5)滑行段

滑行段为无动力飞行段,本飞行段初始时间和状态与三级一次终端一致,需要考虑三级发动机二次点火预冷时间和最长滑行时间的约束条件。

6)三级二次飞行段

三级二次飞行段的终端目标是地月转移轨道,本飞行段初始时间和状态与滑行段终端一致,运动方程约束、终端质量约束与三级一次一致。

飞行剖面与约束条件的对应关系如图1所示。

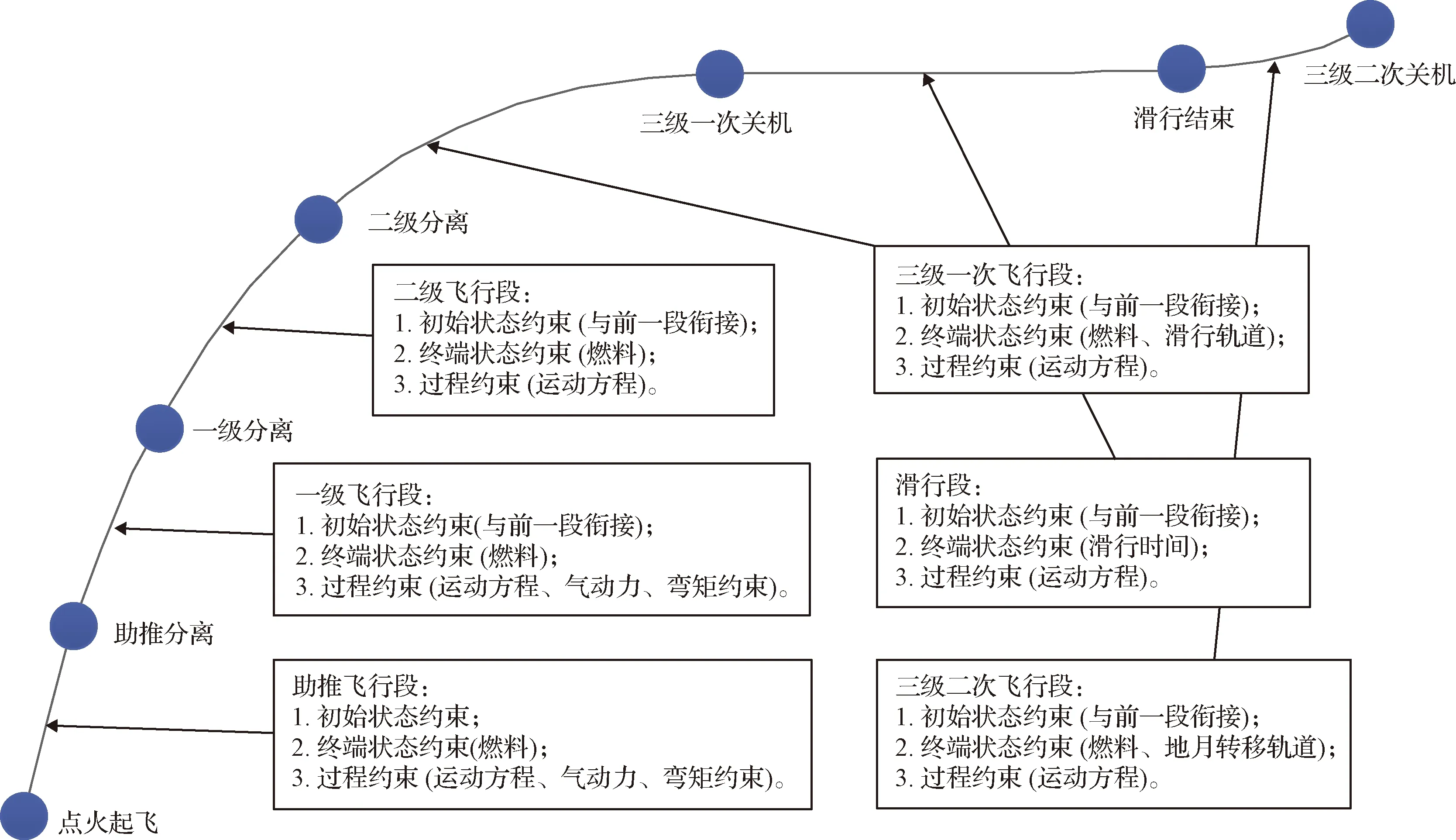
图1 飞行剖面与约束条件Fig.1 Flight profile and constraints

1.2 初始状态约束

(1)

其余各飞行段的初始状态与上一飞行段的终端位置矢量和速度矢量相等,上标j依次对应一级到三级二次各飞行段。

(2)

一级飞行段质量初值为抛掉助推后的火箭剩余质量,二级和三级一次飞行段质量初值与燃料加注量相关,在忽略沉底、预冷、姿控发动机燃料消耗的假设条件下,滑行段和三级二次飞行段的质量初值等于三级一次终端质量:

(3)

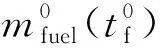
1.3 终端状态约束

各飞行段均需满足最小剩余质量的约束条件:

(4)

滑行段时间需满足飞行时间约束:

(5)

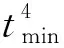
(6)

式中:Funorbit表示速度位置与轨道根数的转换关系;a为半长轴;e为偏心率;i为轨道倾角;Ω为升交点经度;ω为近地点幅角。

1.4 过程约束

在发射点惯性系下描述各飞行段过程约束主要为质心运动微分方程:

(7)

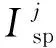
(8)

式中:φdx为地心纬度;μ为引力常数;R0为赤道半径;ΩE为地球自转角速度矢量。

仅在助推和一级飞行段考虑喷口压力损失对推力的影响ΔTj,以及气动力作用和弯矩约束条件:

(9)

式中:q为动压;SA和CD为气动参考面积和气动力系数;Se为喷口截面积;Pe和Pa分别为火箭所在位置的气压和地面气压;α为攻角;Qαmax为箭体结构能承受的最大弯矩。

2 剩余运载能力估计方法

对于第1节描述的多飞行段运载火箭上升段轨迹规划问题,不存在解析形式的解,只能采用数值规划的方式进行求解。自适应配点法作为主流的求解非线性规划问题的数值优化方法,能够在较少离散点个数的条件下达到较高的求解精度,并且在良好初值的前提下,收敛性较好。本节首先根据各飞行段特点,提出了一种提升自适应配点法收敛性的序贯求解方法,然后基于该方法给出了离线估计剩余运载能力的数值求解方法,以及与故障程度相关的剩余运载能力在线判别条件。

2.1 基于飞行剖面的全程轨迹序贯求解方法

根据原规划问题的终端条件,可将其分解为由助推、芯一级、芯二级、三级一次飞行段组成的进入目标滑行轨道的规划子问题,以及由滑行段、三级二次飞行段组成的进入目标地月转移轨道的规划子问题。首先求解目标滑行轨道的规划子问题,以该问题的终端条件作为目标地月转移轨道规划子问题的初始条件,求解滑行段、三级二次飞行段的轨迹,最后对2个问题联立求解,得到火箭全程飞行轨迹。规划问题逐层分解策略如图2所示。

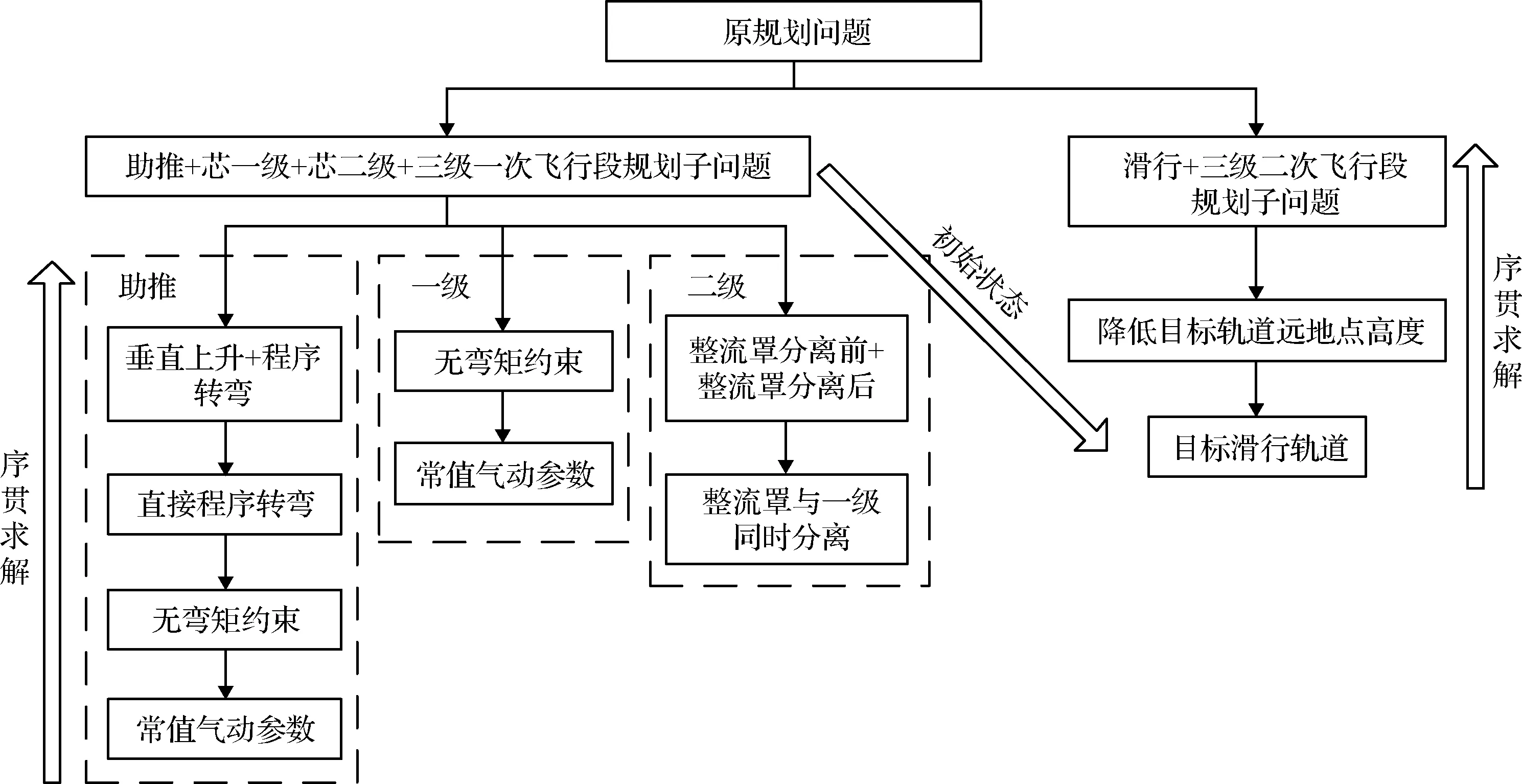
图2 全程规划问题逐层分解策略图Fig.2 Decomposition strategy for trajectory planning problems

对于求解目标滑行轨道规划子问题,依次分析助推段、芯一级、芯二级的约束分解策略。在助推段,首先忽略垂直上升段、假定火箭起飞后直接开始程序转弯,然后忽略弯矩约束,放宽搜索范围,最后为降低气动力非线性对规划的影响,可先将气动参数作为常值考虑。在芯一级飞行段,放宽弯矩约束,并假定气动参数为常值。在芯二级飞行段,可先假定整流罩随芯一级一起分离,降低求解过程中质量突变对规划的影响。

对于求解目标地月转移轨道规划子问题,地月转移轨道终端速度大,迭代求解过程中状态量和控制量细微的调整都将对终端轨道面内约束产生很大的影响。轨道半长轴计算公式如下:

(10)

式中:C3为特征能量[18],其对于速度的偏导数为2V,与终端时刻的速度成正比。运载火箭通过停泊轨道的滑行调整轨道拱线指向,并加速进入地月转移轨道,入轨点在近地点附近,因此入轨时刻速度大。以近地点200 km,远地点380 000 km的地月转移轨道为例,入轨点速度达到10 916 m/s。若数值求解过程中速度修正1 m/s,将导致特征能量变化21 833 m2/s2,相当于半长轴a变化2 138 km。

因此,对于地月转移轨道的规划问题,其目标轨道根数对入轨时刻速度十分敏感,在初始猜想偏差较大时易导致求解过程来回振荡,难以收敛的情况。可在约束目标轨道近地点高度、升交点经度、轨道倾角和近地点幅角的情况下,序贯求解远地点高度较低的飞行轨迹,以前一次解作为更高远地点高度等式约束的初始猜想,直至收敛至满足进入地月转移轨道全部约束条件的飞行轨迹。

2.2 推力下降故障下的剩余运载能力估计

本文重点考虑由于发动机秒流量下降引起的推力下降故障。秒流量下降故障相当于总冲不变情况下,剩余燃料仍可用,在视加速度下降的同时,换来了更长的燃料燃烧时间。在质量微分方程和推力计算方程中引入剩余推力百分比κ:

(11)

对于复杂的多飞行段运动过程,忽略运动方程和约束条件很难实现准确的能力评估,因此采用不同故障状态下规划飞行轨迹的方式,搜索出火箭能够进入原目标轨道的故障适应范围。将式(11)作为新的约束条件引入轨迹规划问题,采用2.1节的序贯求解方法求解。以最小化κ为目标函数,通过遍历不同故障发生时刻tfault和火箭能够入轨的剩余推力百分比κ,得到火箭能够进入地月转移轨道的状态集ST{tfault,κ}和能够进入停泊轨道的状态集SC{tfault,κ}。飞行过程中,根据故障发生时火箭所处的飞行段,判断故障时间和故障状态所属的状态集,从而完成剩余运载能力的迅速评估,如图3所示。

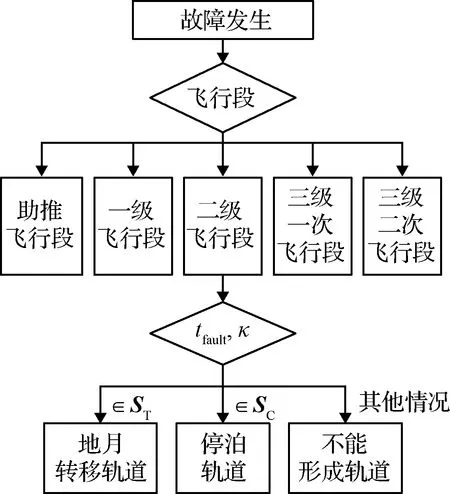
图3 剩余运载能力评估流程Fig.3 Assessment process of residual carrying capacity

3 停泊轨道重规划方法

本节介绍一种基于数值方法的停泊轨道重规划方法。考虑载人登月火箭助推级和芯一级火箭的发动机台数多的特点,在单台发动机出现推力下降故障时,可通过其他发动机的性能提升进行弥补,对运载能力影响较小。对于二级火箭,我国通常采用双发动机的配置,若发生单台发动机推力严重下降的故障,则两台发动机推力不对称将导致其在箭体轴向的分力产生严重的干扰力矩,在推力不足的同时,影响火箭姿态控制的稳定性,即火箭姿态将呈现来回晃动的现象,如图4所示。

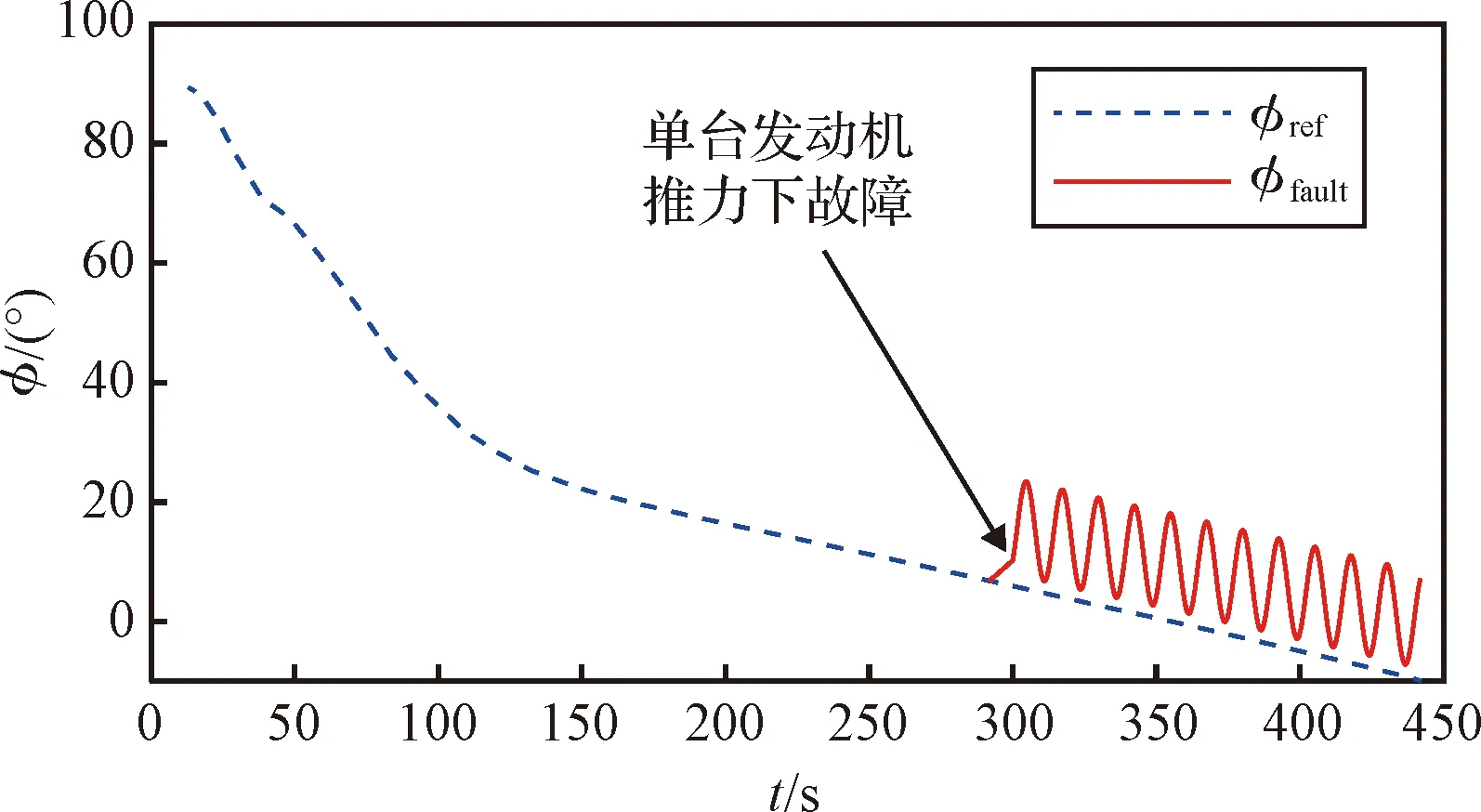
图4 火箭单台发动机故障姿态示意图Fig.4 Rocket attitude after single engine failure

图4中φref和φfault分别为故障前俯仰姿态角和故障后俯仰姿态角曲线。从航天员安全角度出发,本文提出在二级发生严重故障后,火箭直接执行发动机关机和二三级分离的动作时序,通过对三级的重规划飞向停泊轨道。

对于具备二次启动能力的三级火箭,通常认为增加滑行段能够有效提升运载能力。但对于在二级火箭发生严重故障的情况,若设置滑行轨道,则需要考虑滑行时间和三级二次飞行段发动机最短工作时间的限制条件。由于火箭故障时速度较低,且三级火箭过载小于二级火箭,需要借助地球引力的作用,通过降低火箭高度获得速度增量,才可能满足滑行段的条件,然而此时火箭高度较低,在安全的高度条件下不足以提供期望的速度增量。因此,更优的选择是将三级火箭两次点火的控制策略重规划为单次点火,燃料全部用于提升火箭速度和高度。

三级进入停泊轨道的问题描述为

(12)

合适的初始猜想有利于提升式(12)描述的非线性规划问题的求解收敛性,而凸优化方法具有不需要给定初值且收敛性好的特点,于是本节首先给出了基于地心角估计的初始猜想凸优化方法。同时,考虑停泊轨道的近地点高度是确保航天员安全留轨的关键轨道根数,结合终端轨道根数约束强非线性的特点,给出了一种基于状态触发的停泊轨道重规划方法,先求解仅考虑轨道高度的停泊轨道,再结合剩余能力,规划满足更多轨道面约束的安全停泊轨道,如图5所示。

图5 停泊轨道重规划流程图Fig.5 Flow chart of parking orbit re-planning

3.1 基于地心角估计的初始猜想凸优化方法

凸优化的限制在于终端自变量要固定,于是取三级火箭燃料耗尽的时间作为终端时间tk,并且为简化轨道根数约束,在轨道系下描述终端轨道约束:

Funorbit([r,V](tk))

(13)

定义轨道系的原点为地心,y轴由地心指向预估入轨点,x轴在给定轨道面内与y轴垂直指向速度方向,z轴满足右手定则。轨道面由i和Ω决定,为将能量用于提升轨道高度,可取故障时刻状态对应的ifault和Ωfault。因此,预估入轨点的准确性直接决定了凸优化问题是否存在可行解。故障后的运动过程如图6所示。

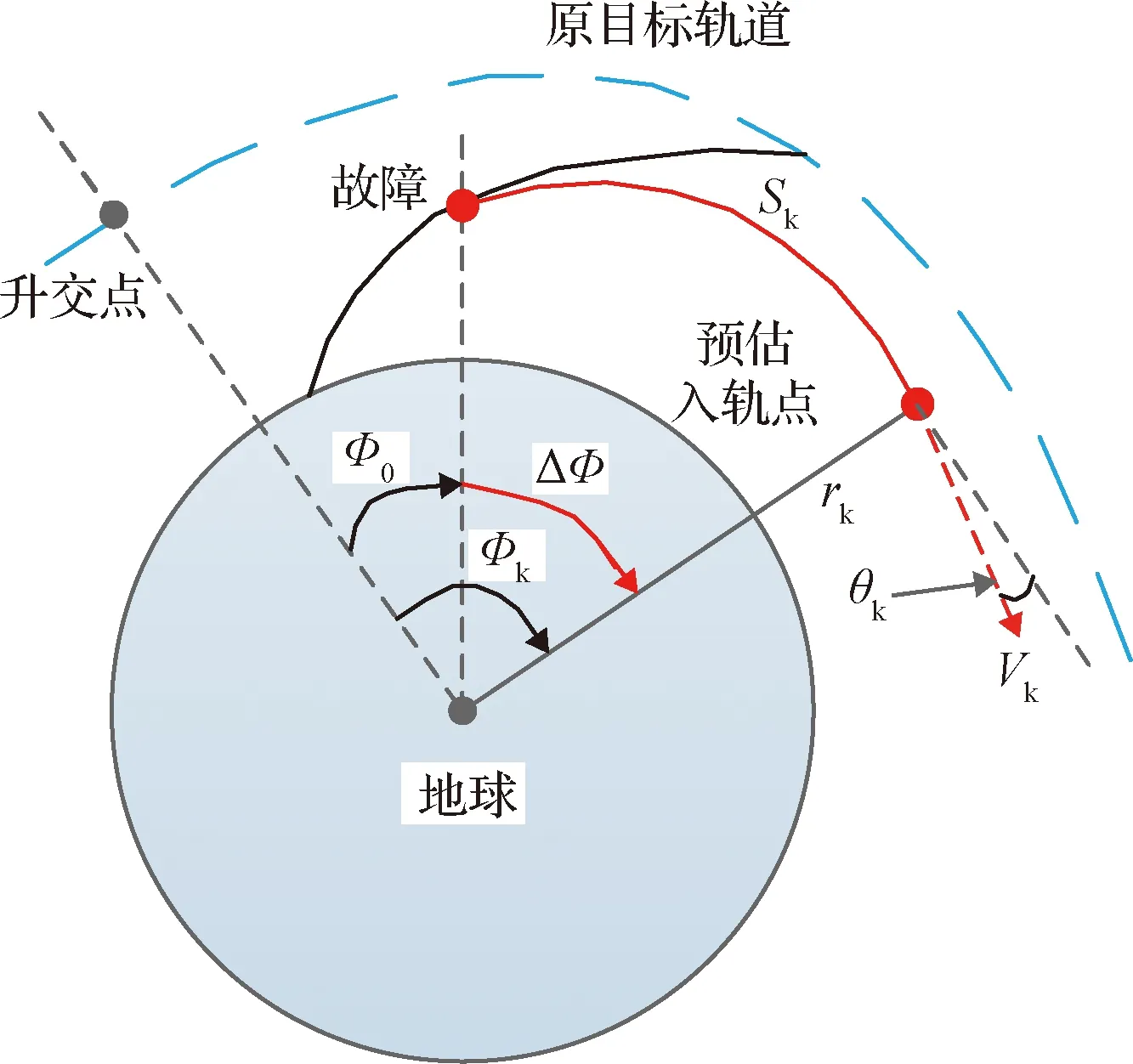
图6 预估入轨点示意图Fig.6 Estimated orbital insert point

本节参考经典迭代制导对入轨点的估计,定义故障时刻位置与升交点之间地心夹角为Φ0,与预估入轨点之间地心夹角为ΔΦ,则预估入轨点地心角Φk可表示为入轨点地心距rk、入轨点速度倾角θk和剩余航程Sk的函数:

(14)

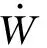
(15)

式中:第1项为视加速度产生的航程;第2项为引力和攻角对航程的影响;积分时长为剩余飞行时间tk。图7为基于地心角估计的初始猜想凸优化流程。

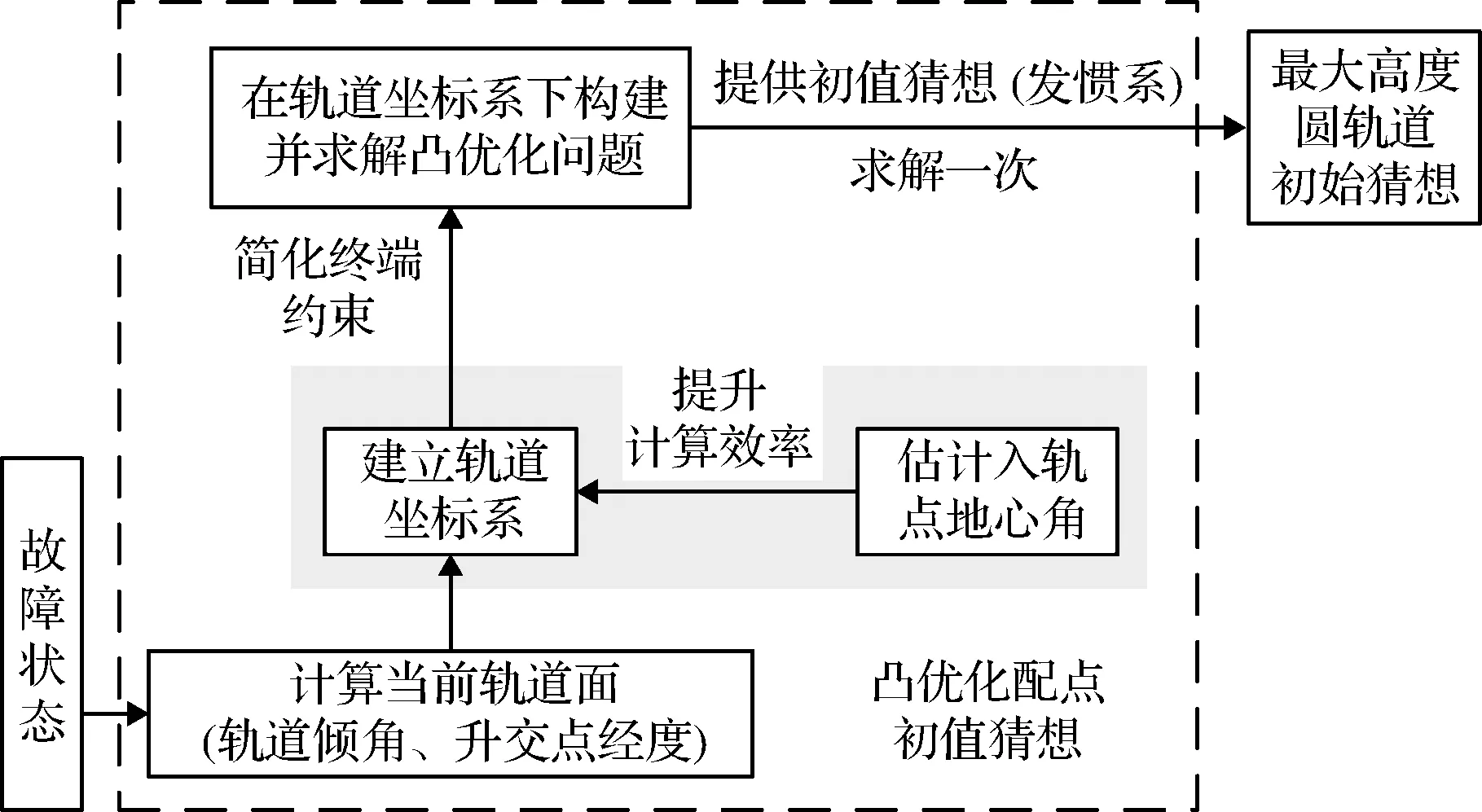
图7 初始猜想优化流程图Fig.7 Flow chart of initial guess optimization

以最大化轨道系下y向终端位置yf为优化目标,采用下式变量代换:

(16)

可建立凸优化命题,如下式所示,并可利用原始对偶内点法迅速求解:

(17)

3.2 基于状态触发的停泊轨道重规划方法

基于状态触发的停泊轨道规划方法见图8。

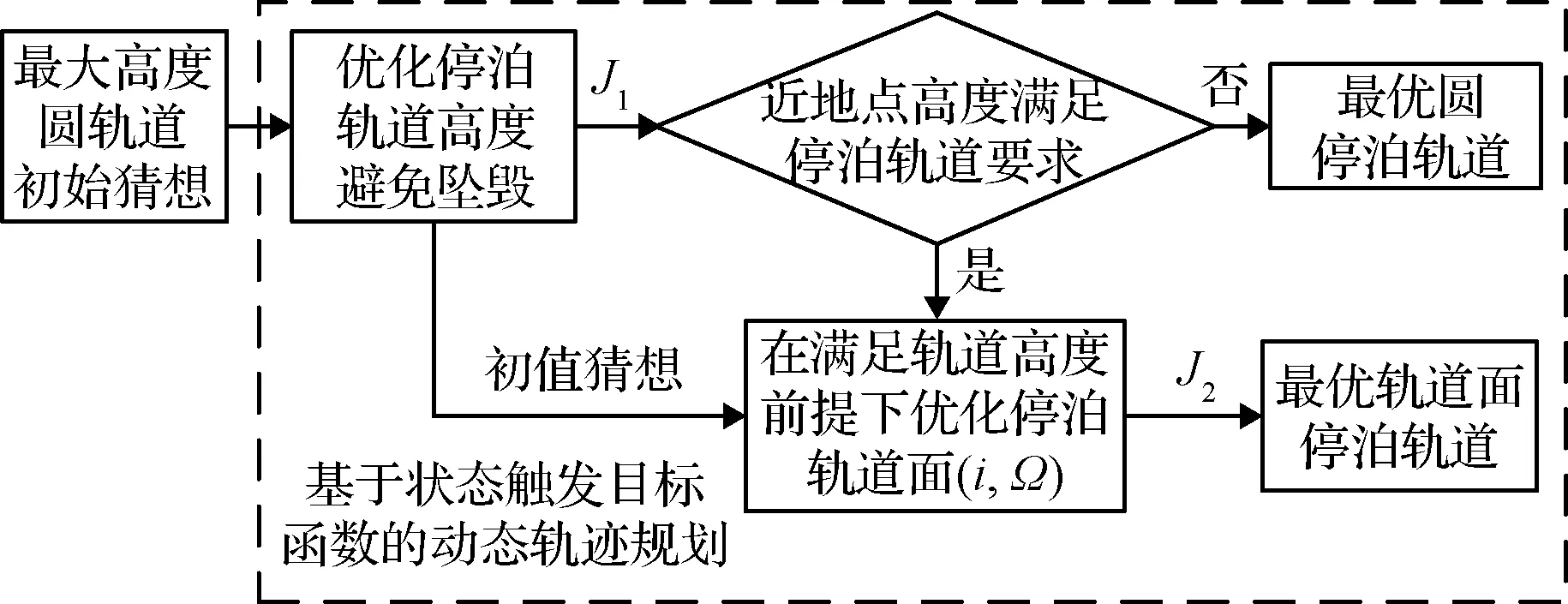
图8 状态触发规划流程图Fig.8 Flow chart of state-triggered planning

在能量相同的条件下,圆轨道的近地点高度最大,因此首先根据3.1节计算的初始猜想,在放开轨道倾角、升交点经度的条件下利用自适应配点法规划最大高度圆轨道。若其优化结果的近地点高度满足停泊轨道要求,则表示火箭有富余的运载能力可用于修正停泊轨道面,否则最大高度圆轨道即为火箭能够进入的最优圆停泊轨道。

考虑圆轨道终端条件偏心率严格为零,即

(18)

为降低其非线性,提升数值求解的收敛效果,将其转换为

(19)

则采用俯仰程序角和偏航程序角作为控制指令的最大高度圆轨道优化问题可表示为

(20)

对于运载能力富余的情况,可加入轨道面约束,使飞船尽可能靠近期望的停泊轨道面,便于飞船后续再入返回着陆场。相比于式(20),可将终端约束中加入地心距等式约束,rf=aexp,即入轨点地心距等于期望的停泊轨道半长轴。

将目标函数改为轨道倾角和升交点经度偏差加全平方和最小的形式:

(21)

以式(21)的解作为初始猜想,进一步优化停泊轨道面,可最大程度利用火箭剩余运载能力,求解出最优轨道面停泊轨道。

4 仿真分析

首先采用本文提出的基于飞行剖面的全程轨迹序贯求解方法,求解三级半构型火箭进入地月转移轨道的上升段全程轨迹规划结果,作为评估剩余运载能力和轨迹重规划的基础,滑行轨道和目标轨道根数见表1。

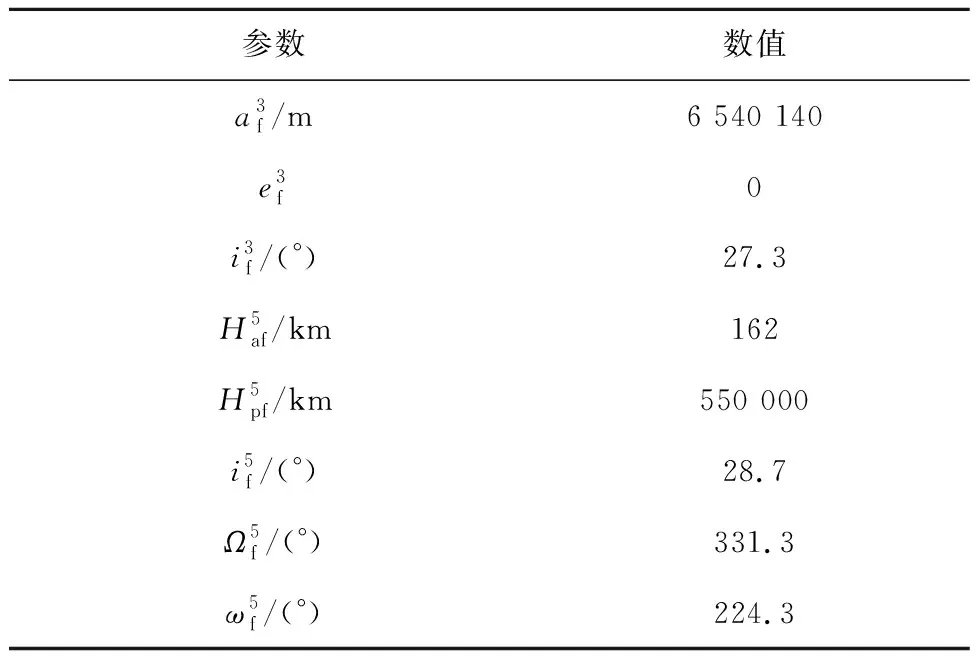
表1 轨道根数Table 1 Orbital elements

规划结果如图9所示。助推器173 s分离,一级火箭227 s分离,二级火箭442 s分离,三级一次飞行段634 s关机后进入滑行段,滑行600 s后进入三级二次飞行段,并于1 966 s船箭分离。

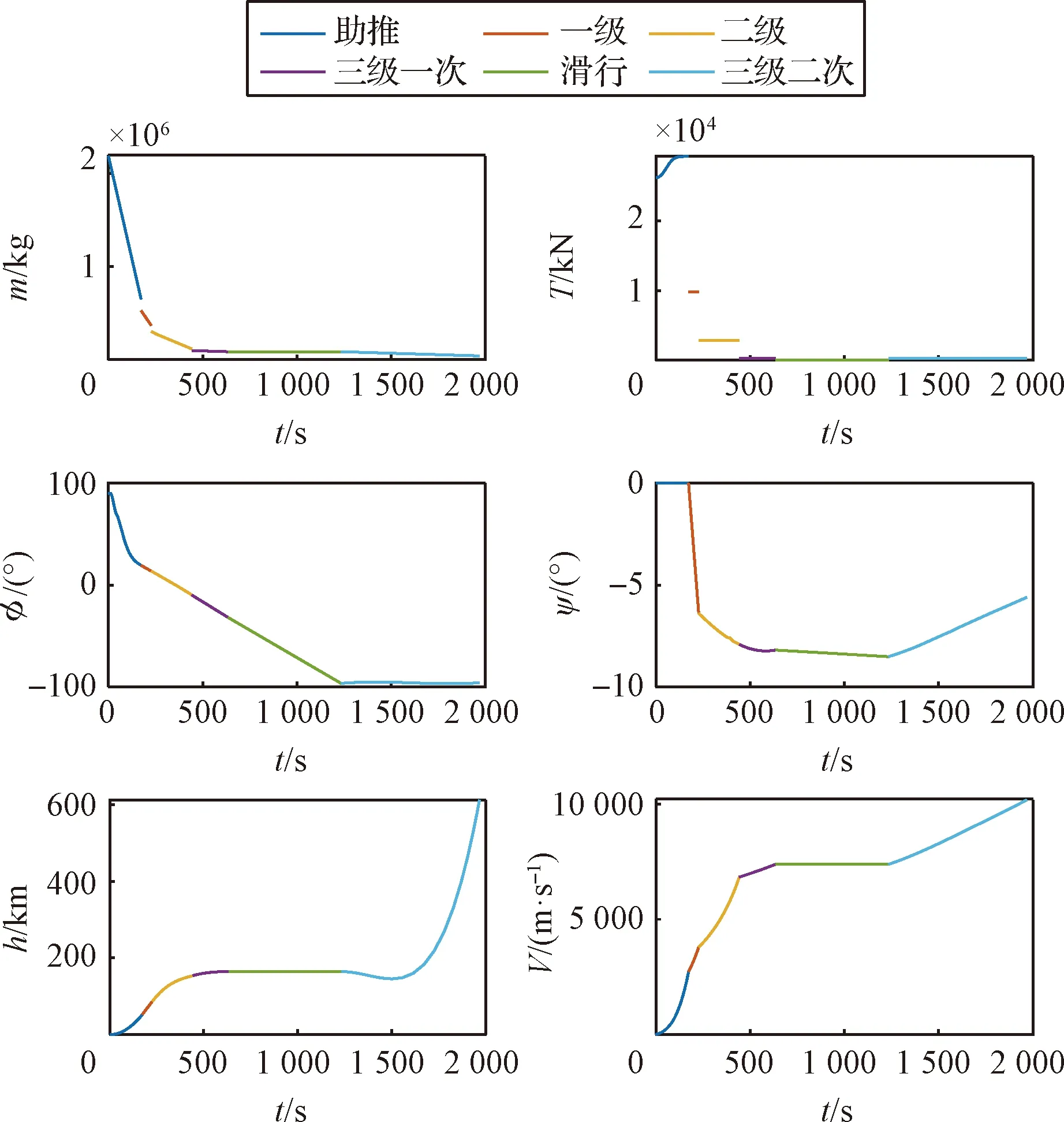
图9 全程轨迹规划结果Fig.9 Trajectory planning results for each phase

4.1 剩余运载能力估计仿真结果

根据2.2节方法,遍历火箭二级飞行段、三级一次飞行段发生因秒流量下降导致的推力下降故障的适应范围。对于三级二次工作段,火箭已达到停泊轨道,本文不讨论其飞行过程发生故障后的停泊轨道重规划问题。

在三级一次飞行段[442, 634] s的时间区间内,以9.6 s为间隔,遍历20个不同故障发生时间对应的剩余推力百分比κ适应范围,如图10所示。

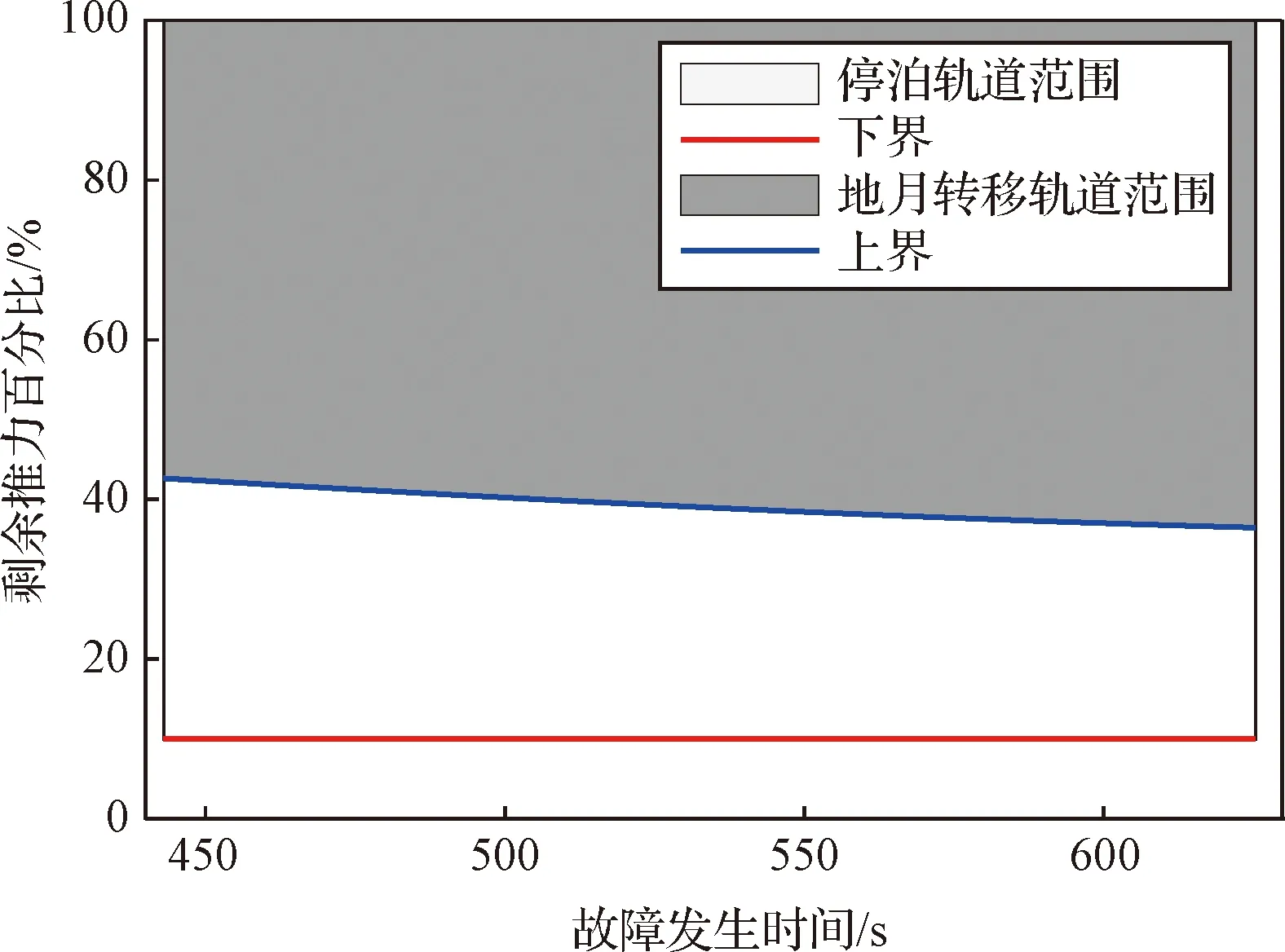
图10 三级一次飞行段剩余运载能力范围Fig.10 Residual carrying capacity range of the first powered phase of the third stage

故障发生时间越晚,能够容忍的故障程度越恶劣。剩余推力大于42%的故障状态下,火箭具备将飞船送入地月转移轨道的能力;在剩余推力大于10%的故障状态下,火箭具备将飞船送入停泊轨道的能力。

进一步验证推力下降后火箭对轨道倾角的调整能力,以三级一次飞行段单台发动机剩余推力50%为例,火箭在满足近地点高度的条件下,不同故障发生时间对应的停泊轨道倾角的上下界如图11所示。

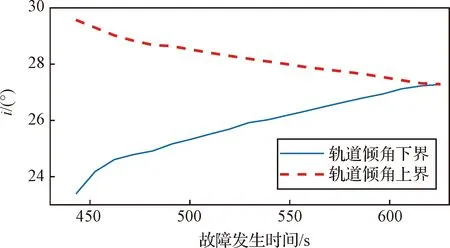
图11 停泊轨道倾角边界Fig.11 Orbital inclination boundary of the parking orbit

当故障发生时间较早时,火箭有更多的时间调整偏航程序角,因此轨道倾角可调整的范围更大;若在接近三级一次关机时发生故障,则轨道倾角处于目标滑行轨道倾角附近。

考虑二级火箭单台发动机失效后直接进入三级飞行段的安全处理方案,假设三级发动机工作正常,则剩余运载能力范围仅与二级飞行段发生故障的时间相关,如图12所示。蓝色虚框表示火箭在420 s后发生故障,仍能够进入地月转移轨道,红色虚框表示火箭在357 s后发生故障,仍具备将载荷送入停泊轨道的能力。从图中可以看出火箭在357 s时高度仅为140 km,速度5 200 m/s,距离形成安全停泊轨道需要近2 200 m/s的速度增量。

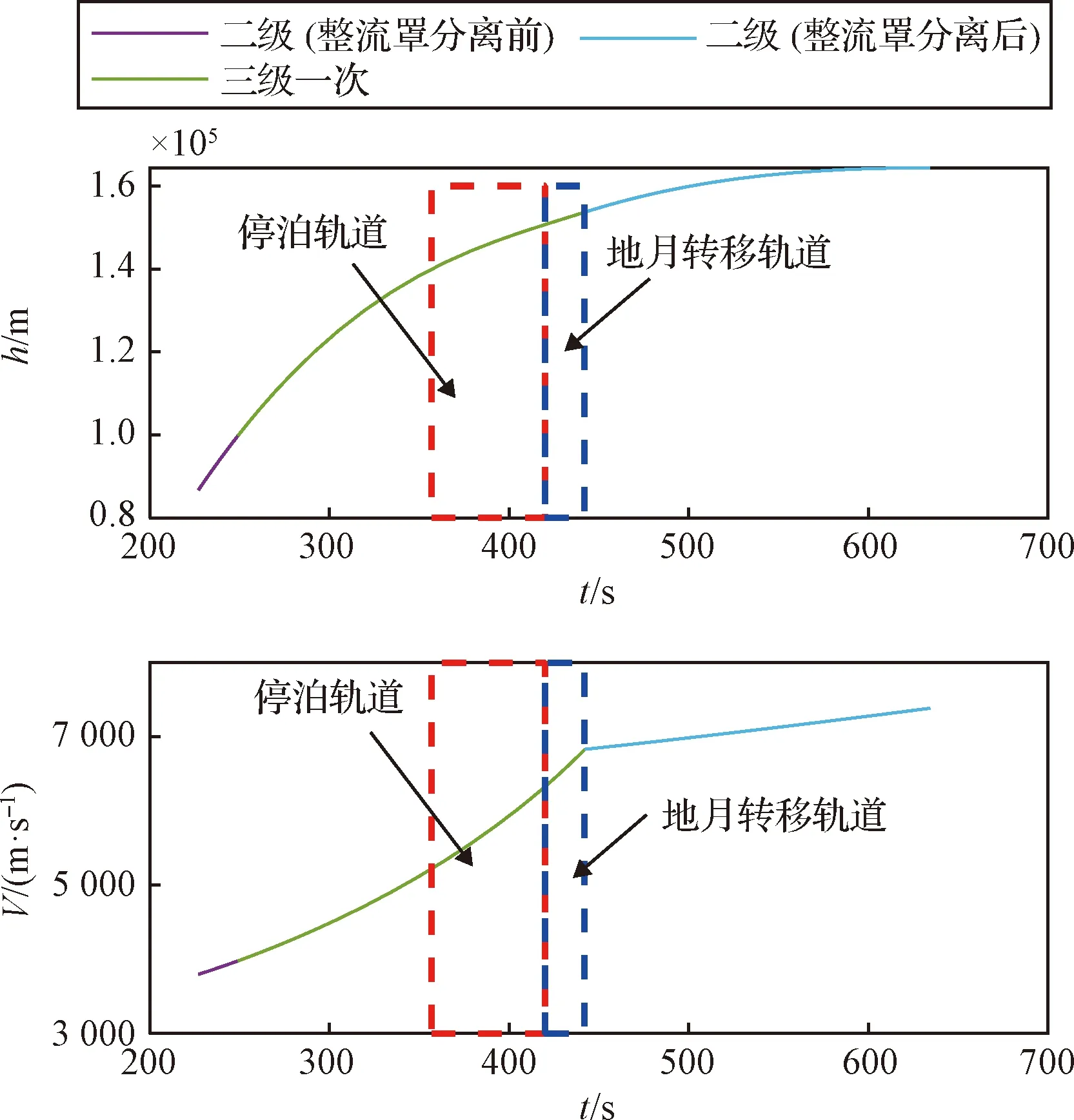
图12 二级飞行段剩余运载能力范围Fig.12 Residual carrying capacity range of the second stage

4.2 轨迹重规划结果

假设火箭在400 s发生严重推力下降故障,关闭二级发动机并在二三级分离后,采用三级发动机将飞船送入停泊轨道。在主频3.6 GHz i7 CPU的台式机上,采用原始对偶内点法计算初始猜想、自适应配点法求解最大高度圆轨道和最优轨道面停泊轨道的迭代次数和求解时间见表2。

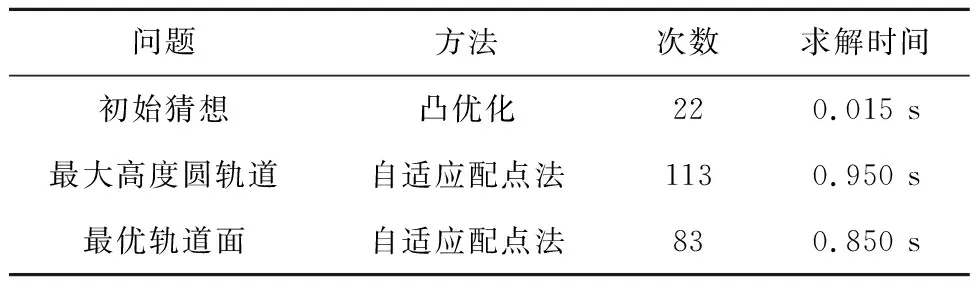
表2 迭代次数与求解时间Table 2 Number of iterations and solution time

求出最大高度圆轨道的时间小于1 s,此时火箭已不存在坠毁的风险,有更多的时间对轨道面进行优化。目标函数值的收敛过程曲线如图13所示。

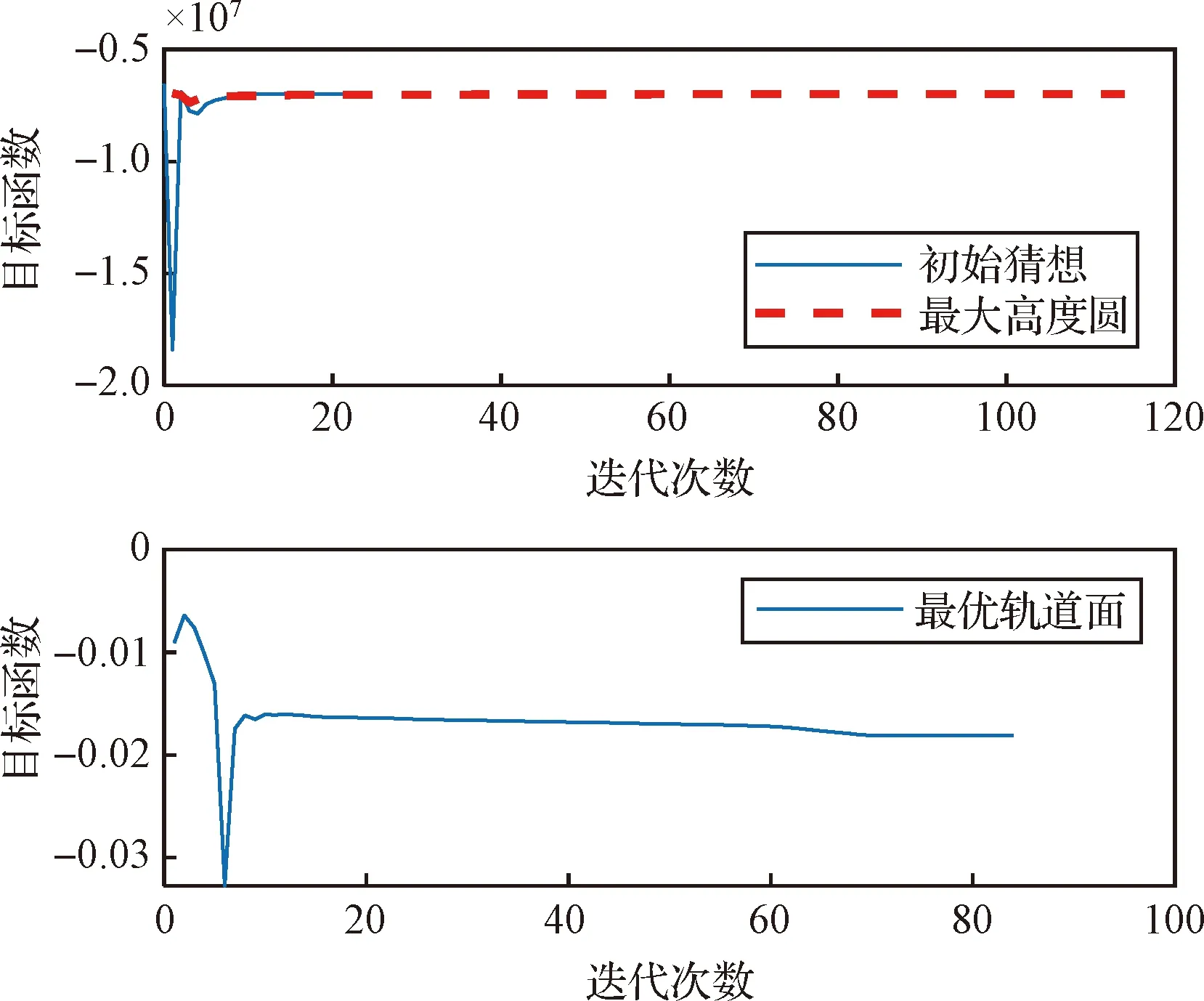
图13 目标函数收敛过程Fig.13 Convergence process of the objective function

初始猜想和最大高度圆轨道的优化目标均为最大化轨道高度,因此,目标函数值小于零。从收敛过程可看出,凸优化计算初始猜想除第1次迭代变化较大外,能够迅速收敛,在迭代10次后,最大高度与最终结果偏差小于1 km;自适应配点法计算最大高度圆轨道由于迭代初值较好,在迭代60次后,目标函数值与最终结果偏差小于1 km。对于最优轨道面的优化,其目标函数值在10次迭代后能够基本收敛。因此本文提出的序贯重规划方法通过合理的设计初始猜想,在迭代次数较少的同时,也具备较好的收敛特性。

轨迹重规划结果如图14所示。初始猜想的结果与最大高度圆轨道优化结果趋势基本一致,能够起到提升非线性规划收敛效率的作用。三级火箭在工作1 001 s后燃料耗尽,对应的最大圆轨道高度为621 km,轨道倾角和升交点经度保持故障时刻的值不变。因此火箭具备将部分运载能力用于调节轨道面的条件,假设期望停泊轨道面参数与标称滑行轨道面一致,主要考虑消除轨道倾角的偏差,令式(21)中ki=1 000,kΩ=1,则规划结果如图中红线所示。规划出的最优轨道面停泊轨道与期望停泊轨道的轨道倾角偏差为0.01°,且火箭燃料仍有剩余,有能力将飞船送入期望停泊轨道。轨迹重规划结果为飞行时间921.4 s,进入轨道倾角27.29°,高度162 km的圆轨道。

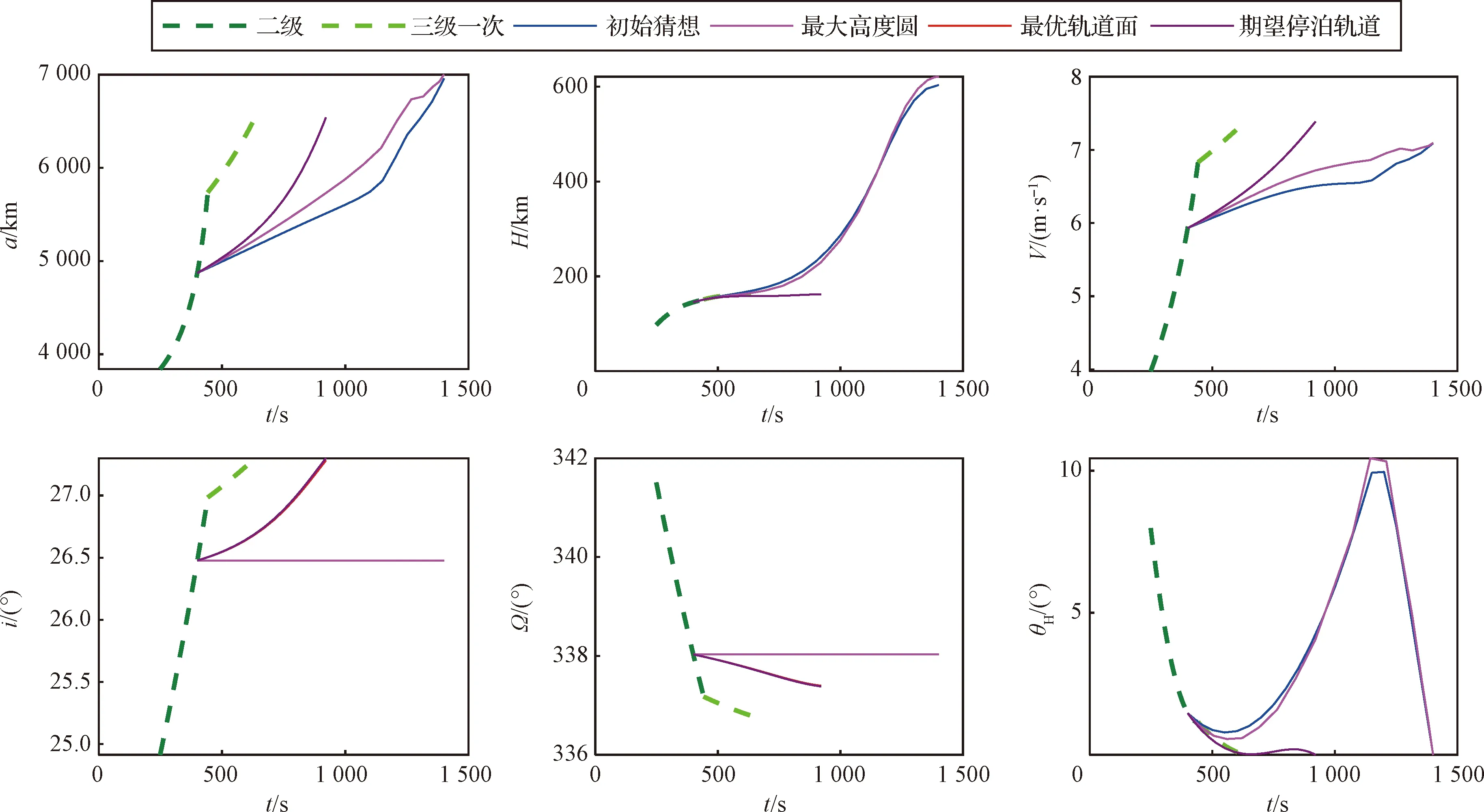
图14 轨迹重规划结果Fig.14 Trajectory replanning results

重规划的程序角曲线如图15所示,由于提前进入三级飞行段,火箭过载变化过程与原轨迹不同,因此程序角与原飞行过程差异较大。规划结果程序角变化率均不大于2(°)/s,过程平缓,能够满足火箭姿态控制系统对角速度变化的需求。

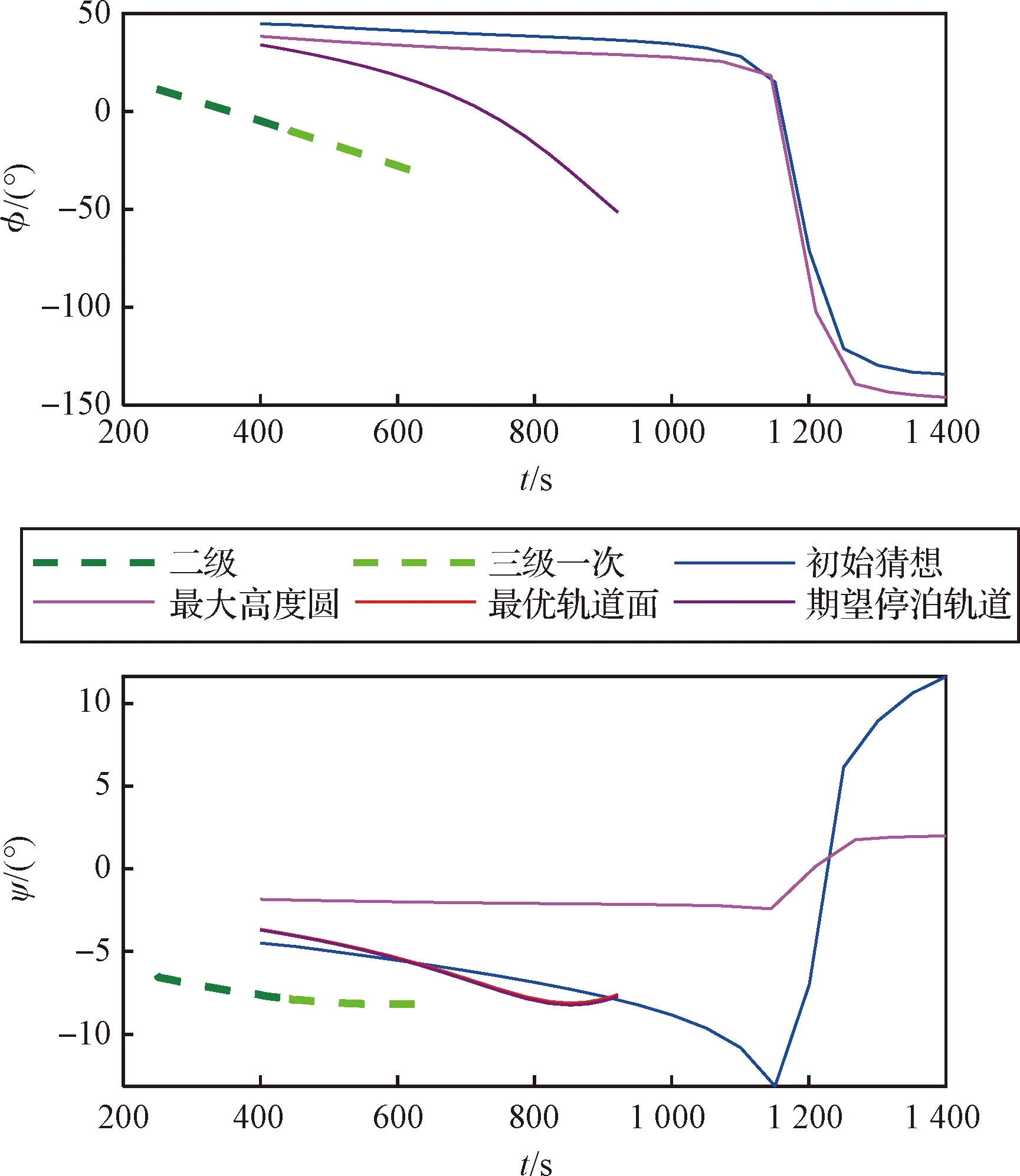
图15 重规划的程序角Fig.15 Replanning guidance command

5 结 论

针对载人登月火箭,建立了上升段全程轨迹规划问题,并基于飞行剖面和约束特点,提出了对原规划问题逐层分解、序贯规划求解的策略,提升了方法的收敛性,可以用于求解秒流量下降故障情况下的剩余运载能力估计问题。通过分析二级火箭发动机配置可能存在的姿控稳定性问题,提出了在二级发生严重故障后直接通过对三级的重规划飞向停泊轨道的方案。从收敛性提升角度,提出了凸优化初始猜想生成方法,参考迭代制导预估入轨点建立轨道坐标系,降低了入轨终端条件非线性度,构建了凸优化问题。提出的综合考虑安全性和计算效率的序贯求解方法,以运载能力作为触发条件,依次优化轨道高度、轨道面、期望停泊轨道。最后,通过数学仿真验证了停泊轨道重规划方法能够在故障状态下迅速判断剩余运载能力,并结合数值优化方法规划出合理的飞行轨迹和相应的程序角指令。