基于能量和循环平稳检测的双门限两层感知算法

唐晓倩，宋 哲，张 怡，盘 晴，张文洁

（1.西安航空学院电子工程学院，陕西西安 710077；2.西北工业大学 电子信息学院，陕西西安 710072；3.西北工业大学计算机学院，陕西西安 710072）

随着移动通信技术的飞速发展，频谱作为无线通信的重要组成部分，正变成越来越紧缺的资源。频谱资源不足是制约无线通信发展的重要瓶颈之一[1]，而造成这一问题的主要原因是：一方面，绝大部分频谱资源已被传统通信系统以及现有用户占据，只有少量资源预留给新的用户和新兴业务[2]；另一方面，现阶段频谱资源分配方式是静态的，导致频谱资源的利用率不高，利用率仅为15%～85%，对频谱资源并未充分利用[3]。为了满足日益增加的频谱需求，Joseph Mitola 博士于1999 年提出了认知无线电（Cognitive Radio，CR）技术[4]。认知无线电系统对周围的信道环境进行实时感知，在不影响授权用户正常通信的情况下，自适应地占用频谱空穴加以使用，从而可以有效提高频谱资源的使用效率[5]。

频谱感知技术是认知无线电的核心技术之一，目前常用的频谱感知算法有能量检测法、循环平稳检测法和匹配滤波法[6-7]。其中，循环平稳检测法适合应用在低信噪比的信道环境中，但是该检测法计算复杂，会导致检测时间过长的问题[8]；匹配滤波法在进行测量之前，需要获取目标信号的先验参数，因此在信号未知的情况下应用受限；而能量检测法算法复杂度低，不需要被测信号的先验信息，在硬件上容易实现，但是在低信噪比信道中会发生漏检[9]。

文中提出了一种基于能量检测和循环平稳检测的双门限两层感知算法，即先采用能量检测法检测信号，当信号的能量统计量位于双门限之外时，可直接给出判决结果，而对于能量统计量落入两个门限之间的信号，则采用循环平稳检测法进行第二层检测。仿真实验表明，新的检测方法可以有效克服循环平稳检测法计算难度大以及能量检测法在低信噪比环境检测性能差的问题。

1 能量检测法

1.1 传统能量检测法

能量检测法是目前最常用的、具有较强普适性的频谱感知方法[10]，其算法流程图如图1 所示。该方法方便快捷，在硬件上容易实现，可以通过适当增加FFT 的采样点数来提高算法的感知精度[11]。

图1 能量检测法流程框图

频谱的检测问题可以抽象为一个二元假设问题：

其中，x(n)为主用户的发射信号，y(n)为认知用户的接收信号，w(n)为0 均值、方差的高斯分布白噪声，H0代表信道频谱中无主用户存在情况，H1代表信道频谱中存在主用户的情况。

首先，将认知用户接收到的信号通过一个中心频率为fc的带通滤波器，选择出目标频段。其次，将输出信号进行平方运算，最后在时间T内积分就能得到能量统计值Y。信号能量统计值Y可以用以下公式表示：

其中，N为采样点数。

计算得到能量统计值Y之后，将其与设定的门限值λ进行比较，若Y＞λ，则系统将判定当前时刻信道频段上存在主用户；反之，若Y＜λ，则系统判定当前时刻信道频段未被主用户占用。

1.2 双门限能量检测法

传统的能量检测法通常只用一个判决门限进行判决[12]，而双门限能量检测法在此基础上增加了一个门限，采用上、下两个门限对统计值进行判决。其具体判决图如图2 所示。

图2 双门限能量检测法判决图

在上述判决图中，上门限值λ1和下门限值λ2的表达式分别如下：

其中，a0为在H0情况下进行检测的认知无线电用户不发送任何判决结果的概率。

2 循环平稳检测法

2.1 检测原理

循环平稳检测法主要通过对接收信号自相关函数进行计算，利用其周期性特点进行相应的判决[13]。通信系统中的信号一般都是循环平稳信号，而噪声属于广义平稳信号，在频谱相关函数上不会影响主用户发射信号的特征[14]。因此，这种通过分析信号频谱自相关函数的特征来分辨信道上是否有主用户存在的方法，即使在低信噪比环境下，也可以有效地区别噪声和已调信号[15]。循环平稳检测法的算法流程图如图3 所示。

图3 循环平稳检测法算法流程图

2.2 算法模型

若系统的接收信号x(t)具有二阶平稳特性，则零均值的离散二阶时变自相关函数Rx(α,τ)=E{x(t)·x(t+τ)}为周期函数。设周期为T0，存在以下傅里叶变换对：

其中，各未知参量如式（11）-（13）所示，W(T)(s)表示长度为T的Kaiser 窗。

将统计量TR(α)与门限值λ相比较，若TR(α)＞λ，则主用户信号存在；反之，主用户信号不存在。

检测概率Pd和虚警概率Pf分别可以表示为：

循环平稳检测具有良好的检测性能，但由于算法中包含两次傅里叶变换处理，计算复杂，以至于检测时间过长。

3 双门限两层感知算法

3.1 算法原理

传统能量检测法和循环平稳检测法都有各自的优点与缺点。能量检测法的优势在于算法简便，有利于实时处理，但是在噪声较强的环境下效果不理想；而循环平稳检测法抗干扰性好，检测性能优异，但是计算量过大，难以保证实时性[16]。因此文中结合两种算法的优点，提出了一种双门限两层感知算法。新算法基本原理：首先对接收信号进行第一层感知，即用双门限能量检测法处理信号，若能量统计值大于上门限，则认为当前信道上有主用户存在；若能量统计值小于下门限，则判定主用户不存在；若能量统计值位于两个门限值之间，则进入第二层感知。第二层频谱感知采用循环平稳法进行检测，若检测统计量大于门限值，判定主用户存在；反之主用户不存在。双门限两层感知算法的实现流程如图4所示。

图4 双门限两层感知算法流程图

3.2 实验仿真与分析

基于能量检测和循环平稳的双门限两层感知算法具体仿真步骤如下：

Step1：参数初始化。设定虚警概率Pf、数据长度L、采样数N及采样时间t等基础参数。

Step2：生成待检测信号。其中授权用户采用BPSK 调制信号，噪声为加性高斯白噪声。

Step3：进行第一层感知。根据设定的虚警概率Pf计算出上门限λ1和下门限λ2，由式（2）计算出能量统计量Y，将其与门限值做比较。

Step4：进行第二层感知。对于能量统计量位于双门限内的信号，由式（9）推算出检测统计量TR(α)，若TR(α)＞λ，则判定主用户存在，即H=1，否则H=0。

Step5：综合两层感知结果，计算检测概率Pd。

图5 和图6 均为传统能量检测法、循环平稳检测法以及双门限两层感知算法的检测性能比较曲线。其中，图5 中的虚警概率固定为0.05，图6 中信噪比固定为-7 dB。由仿真结果可以得出，双门限两层感知算法的检测性能优于传统单门限能量检测算法，但低于循环平稳检测法。

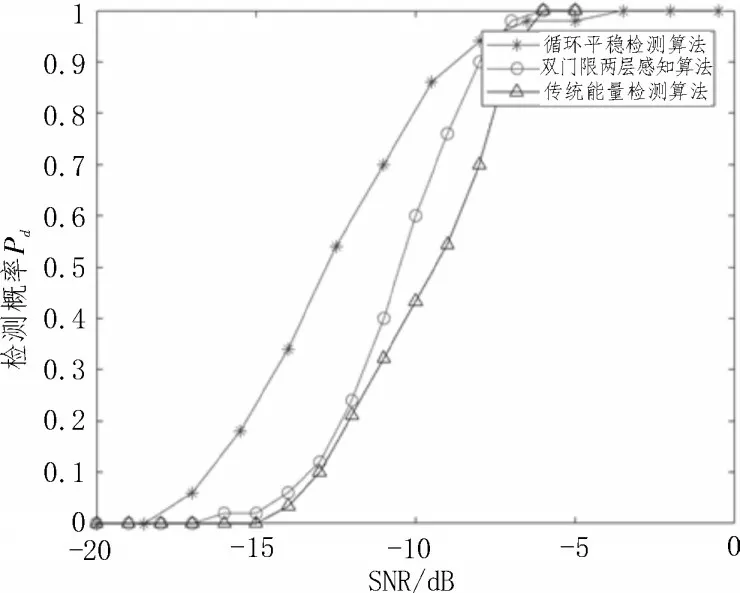
图5 检测概率随信噪比变化曲线

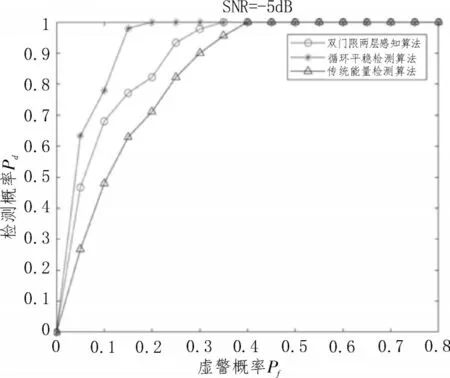
图6 检测概率随虚警概率变化曲线

假设数据的长度为N，窗长为L=N/4-1，则传统能量检测算法的实数乘法次数为N；双门限能量检测算法的实数乘法次数为N+1；循环平稳检测算法的乘法次数为2N2-6N+10，能量检测法、循环平稳法的计算复杂度随N的变化如图7所示。假设能量统计量落入两个门限值之间的概率为P，则双门限两层感知算法所需实数乘法次数为N+1+P(2N2-6N+10)，显然双门限两层感知算法的计算量大于传统能量检测法，但小于循环平稳检测法，其与传统能量检测算法和循环平稳检测算法的计算复杂度对比如图8 所示。当信道处于低信噪比环境时，能量统计值落入两个门限之间的概率会增加，此时，双门限两层感知算法的计算量也会随之增大，其实质是牺牲了算法的实时性来保证检测的准确性。

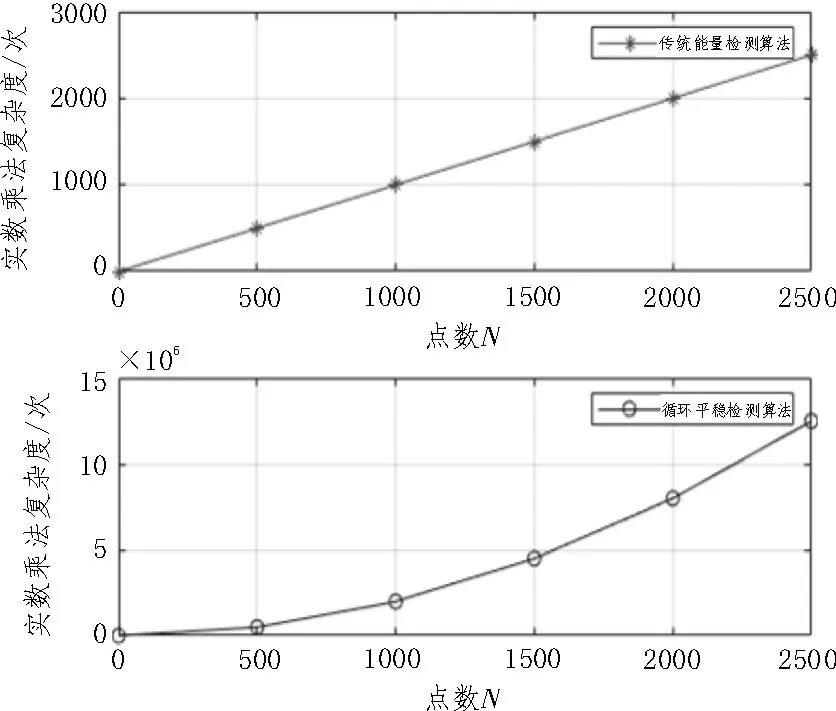
图7 能量检测、循环平稳算法复杂度

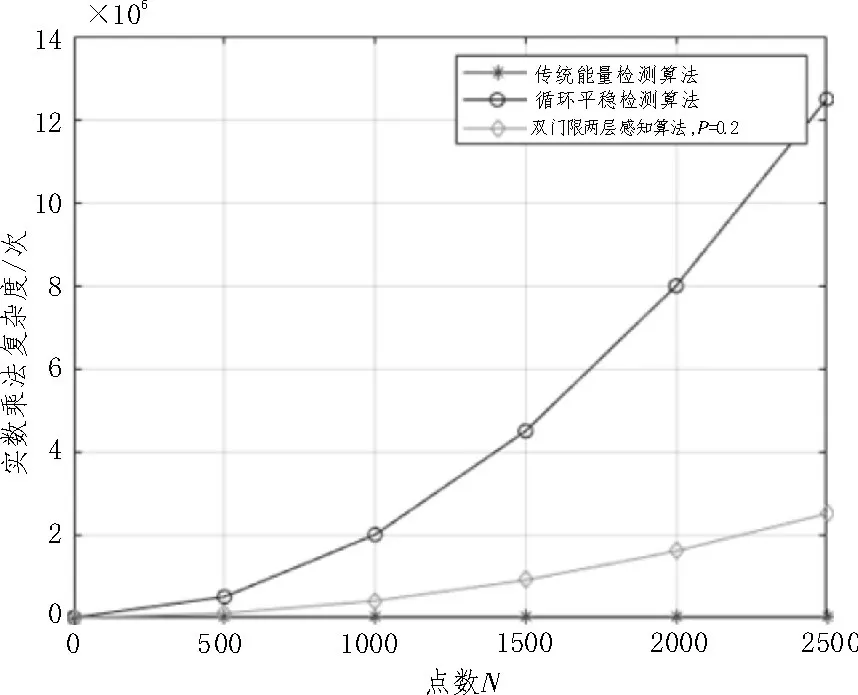
图8 三种算法复杂度比较

通过上述实验结果与分析可知，双门限两层感知算法较传统能量检测算法而言，在低信噪比环境的检测性能具有显著提升。虽然循环平稳检测法在区分信号和噪声方面优于双门限两层感知算法，但在实际频谱感知工作中对感知系统实时性要求较高，因此，在感知速度方面，双门限两层感知算法相对于循环平稳法来说更能满足系统要求。由此可见，双门限两层感知算法很大程度上弥补了传统单用户检测算法的缺点，利用两层感知策略巧妙的将两种感知算法的优点相结合，提升了整体算法的速度与鲁棒性。

4 结论

文中结合能量检测法和循环平稳检测法的优点，提出了一种双门限两层感知算法。对能量检测法、循环平稳检测法和双门限两层感知算法的检测性能及算法复杂度进行了仿真比较，通过对实验结果的分析表明，双门限两层感知算法在低信噪比环境下的检测性能明显优于传统能量检测法；此外，其计算复杂度相对于循环平稳检测法也有极大程度的降低，提升了算法的计算速度。文中所提出的算法为认知无线电中频谱感知技术和策略提供了新颖的思路。