对空观察哨双站测向交叉定位误差分析与验证∗

孟圣波 李鹏飞 黄建廷

（陆军炮兵防空兵学院 郑州 450000）

1 引言

现代防空战场，由于对空侦察雷达受目标散射特征、地物杂波、气象条件、地球曲率以及地形地物遮蔽等因素的影响，对高度100m 以下的超低空目标很难进行有效探测和稳定跟踪。通过对近些年从陆空对抗演习中获取的数据分析来看，演习中一旦蓝军战机进入攻击阵位并采取超低空突防战术时，对空侦察雷达的平均有效预警时间比不足20%［1］。低空预警的能力不足很容易造成火力单元的准备时间不足，给防空战斗带来很大被动，甚至导致整个防空战斗的失败。当前，对空侦察雷达网对超低空突防飞机发现难的问题已成为制约防空兵作战效能发挥的瓶颈。因此，拓展新手段进行超低空目标探测是当前防空兵发展的迫切需要。

回顾我军防空作战的历史，对空观察哨凭借自身机动灵活、抗干扰性强、可前伸布置等优势，在对超低空目标的侦察中始终发挥着积极作用。若观察哨携带具有高精度测角功能的光学侦察器材组成双观测站，通过交叉定位的方法可实现对超低空目标的定位跟踪。但由于侦察器材存在测角误差，导致双站交叉定位结果也会存在误差，而且该误差范围受双站基线长度、目标与观察哨相对位置关系等诸多因素的影响而变化。若不能正确把握定位误差的变化规律，双站布设不合理时就很难获取符合军事需要的空情信息。目前，对双站测向交叉定位基本原理研究的成果较多，但对其误差变化规律的分析较少，不足以支撑对空观察哨在实战中的运用。因此，本文基于双站测向交叉定位的原理研究不同布站方式下定位误差的变化规律，总结出更为合理的布站方案，为提升对空观察哨在实战中的应用质效提供支撑。

2 对空观察哨双站交叉定位的模型

2.1 理想的双站交叉定位模型

双站交叉定位即利用两个高精度测向装备在不同的位置对目标进行测向，而后将所得测向数据和两站间的基线距离通过三角运算处理，确定目标的空间位置。将此问题放在坐标系中研究，其相对位置关系可用图1所示。

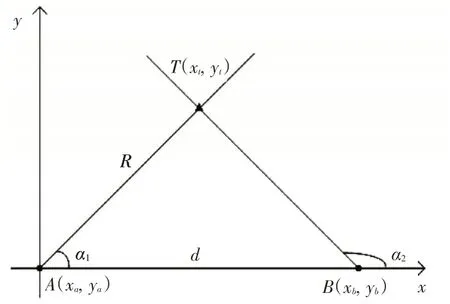
图1 双站交叉定位相对位置关系

为方便进一步分析，假定主站A 位置为原点，主站A 至辅站B 的方向为x 轴的正方向，则A 站坐标（0，0），B 站坐标（xb,yb），目标T 坐标(xt,yt)。两观察哨间距离为d，所测目标仰角分别为α1、α2则可计算目标距离主站A的距离为

根据图1可得以下联立方程组：

求解可得

从以上过程可以看出，只要知道两观察哨的位置及所测目标仰角α1、α2，就可以计算出目标T 的坐标位置(xt,yt)及其与主站间的距离R。

2.2 实际应用中的双站交叉定位模型

在实际应用中，由于光学侦察器材自身存在测角误差，两站所测目标的仰角α1、α2也必定会存在一定的差值。当使用相同的设备进行双站交叉定位时，其测角误差均为θ，便会形成如图2中EFGH所示的定位模糊区。若定位误差过大则难以将观察哨空情和雷达空情进行关联，也就无法满足空情融合的需要。因此只有定位误差符合一定精度要求时观测到的空情信息才有效，所对应的布站方案才可行。于是本文以最大误差距离Dismax≤50m为符合定位要求的限定条件展开研究。

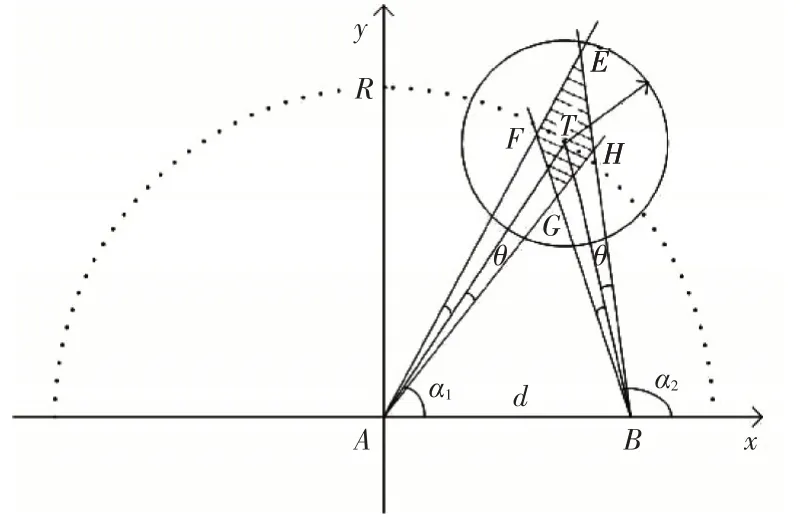
图2 有误差情况下双站交叉定位模型

根据上述模型，可以求得T、E、F、G、H 各点坐标：

由此可计算出最大误差距离Dismax：

3 实验及结果分析

3.1 仿真实验

3.1.1 仿真流程

式（9）为最大误差距离的计算方法，为了研究其在不同布站方式下的变化规律，本文利用Matlab软件进行仿真分析。假设观察哨最大探测距离为R，令主站A 固定于坐标原点，辅站B 可沿x 轴方向移动，主辅站之间的基线距离为d。本仿真实验主要研究当目标在距离主站为R 的圆上做如图2 中虚线所示得圆周运动时，两站对目标实施交叉定位的精度受基线距离d 和主站仰角α1两个变量的影响情况。通过对比分析得出在主站探测距离不变时，不同基线距离下，交叉定位最大误差距离的变化情况。

设R=8km，A、B 两站所测目标仰角α1、α2的取值范围均为（0，180°），光学侦察设备的测角误差θ为1 密位（0.06°）。为了对定位误差进行充分对比，取基线距离与探测距离满足(dR)三种关系的多组数据进行仿真，本文重点分析了基线距离d 依次取4km、6km、8km、10km、11.3km、15km 的6 种布站方式下的定位误差情况。根据以往的研究结果，当目标与两观察点距离相等且为等腰直角三角形时交叉定位的模糊面积最小，由此认为，时可能具有较高的定位精度，故添加了基线距离这一数据进行对比，确定的仿真流程如图3所示。

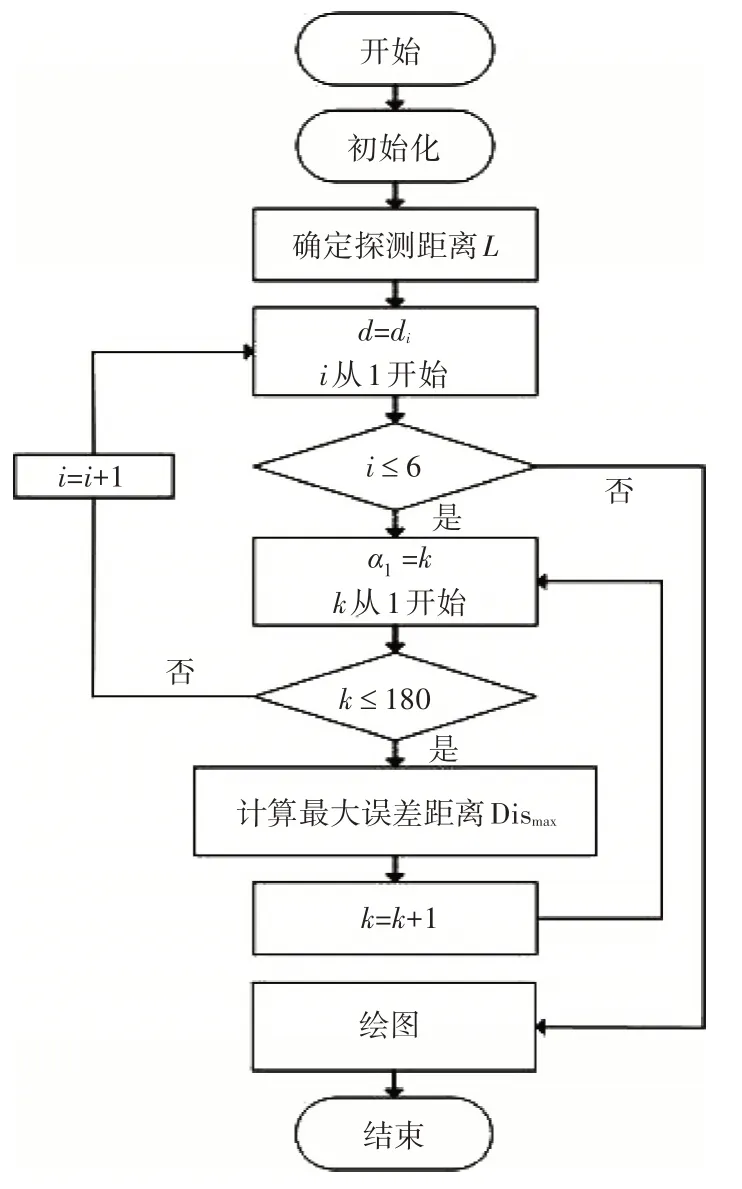
图3 仿真流程图

3.1.2 仿真结果分析

本文将符合定位要求的主站所测目标仰角α1的取值称为主站有效观测区间，若有效观测越广，说明对应的布站方案越合理。对7 种不同布站方式下的数据进行梳理汇总后，得出图4 所示的定位最大误差距离与主站测量仰角对应关系图，表1 则是不同布站方式下主站有效观测区间汇总表。

表1 主站有效观测区间统计表

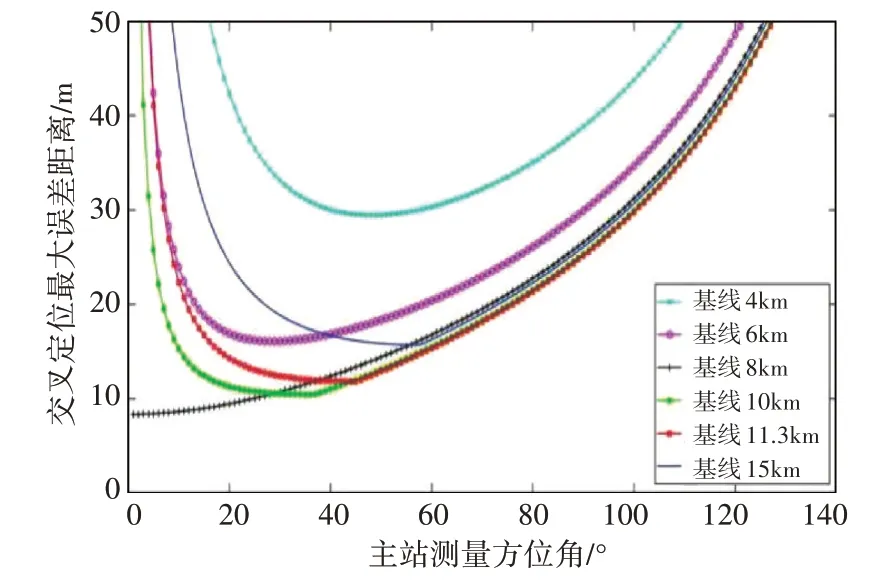
图4 探测距离为8km时的仿真结果

分析图4 和表1 可知，在0°<α1≤28°情况下，d=R=8km 时定位误差最小；29°≤α1≤44° 情况下，d=10km 时定位误差最小；45°≤α1≤127°情况下，d=R≈11.3km 定位误差最小。汇总以上数据发现，符合定位误差最小条件的基线距离与探测距离一直满足R≤d≤R，且在此条件下主站有效观测区间都比较广。因此，基线距离与探测距离满足R≤d≤R关系时的布站方案最合理。

为了验证以上结论的准确性，利用此方法继续对探测距离为5km、3km 两种情况进行仿真和分析，得出图5、表2所示结果。

表2 主站有效观测区间统计表

图5 仿真结果图

综合图5、表2得出以下结论：对空观察哨使用高精度光学侦察器材进行双站交叉定位可以获得有效空情，且在合理布站的情况下能较大程度降低定位误差。布站基线距离与探测距离满足R≤d≤R关系时所对应的布站方式定位精度高、主站有效观测区间广，此范围为最优布站基线距离范围。

3.2 实测实验

为了进一步验证研究结论的准确性，本文开展了利用观察哨组网超低空侦察监视系统对无人机进行双站交叉定位的实装验证，分别在3 种不同基线距离对无人机航迹上的5 个不同测量点进行定位，实验过程如图6所示。

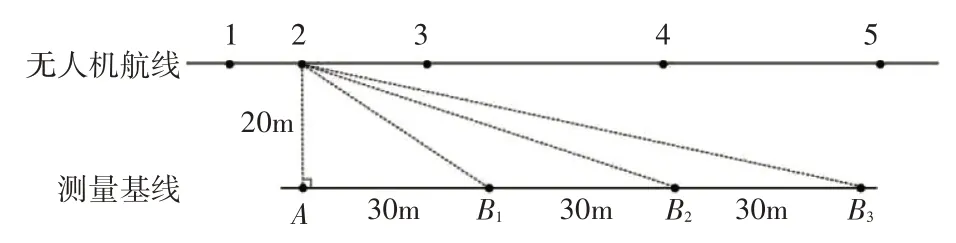
图6 实验示意图

3.2.1 实验步骤

实验中，将观察哨1站固定部署在A点，观察哨2 在距离A 点正东方向30m、60m、90m 处的三个观测点B1、B2、B3部署，双站对无人机航线上的5 个测量点进行交叉定位。无人机在与测量基线平行且相距20m的航路上由东向西飞，经过每一个测量点时在空中悬停，此时1 站位于A 处，2 站分别在B1、B2、B3处与A 站同时对无人机观测，待三个观测点全部完成定位和记录工作后，无人机再飞行至下一测量点，1、2 站再按照上述步骤实施测量，记录数据如表3所示。

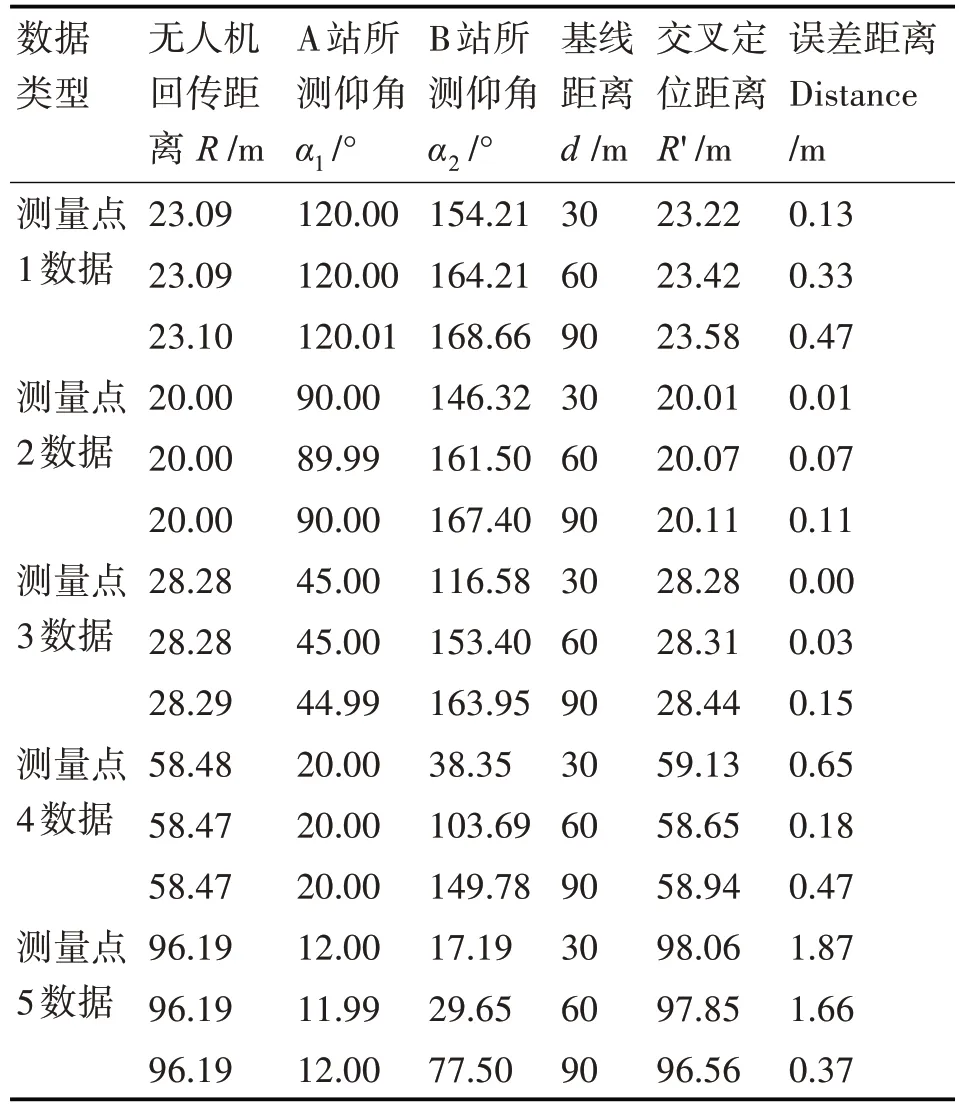
表3 实验测量及计算结果

3.2.2 实验结果及分析

分析以上实验结果，在测量点2 的三组数据中，基线距离与探测距离均满足d> 2R的关系，此时d 越接近 2R时误差距离越小；测量点5 的三组数据中，基线距离与探测距离均满足d

4 结语

本文通过理论分析与实验相结合的方式对双站测向交叉定位误差的变化规律进行了深入分析，着重研究了不同布站方案对定位精度的影响，并得出了优化布站基线长度范围，为光学观察哨优化部署提供了数据支撑，有效提升对空观察哨上报空情质量，为其在实战中的应用提供帮助。但双站交叉定位在观测角度上仍有一定的局限性，若运用更多的观察哨组网构成一种分布式多传感器的广域监测系统，可以在更大区域内实现对目标更精准的定位，其优化布站理论有待进一步研究。