基于相空间重构与GSA-LVQ的有载调压变压器分接开关机械故障诊断

赵书涛,李小双,李大双,徐晓会,李云鹏,李波

(华北电力大学 电子与电气工程学院,河北 保定 071003)

0 引 言

随着电网的快速发展以及国民对电能质量的要求提高,有载调压电力变压器得到越来越广泛的应用,在电力系统中起着调节潮流和稳定负荷电压的作用。有载调压变压器通过其唯一可动部件分接开关(OLTC)来实现调节功能,随着调节的次数增多,OLTC故障的几率就会增加。据国内外资料显示,机械故障是有载调压变压器的主要故障类型[1],这不仅会损坏分接开关和变压器,还会影响电力系统正常运行。对OLTC进行在线监测与故障诊断,就能够及时发现潜在故障,对电力系统安全运行具有重大意义。

OLTC在线监测和故障诊断技术起步于20世纪90年代,其中最常见的是记录传感装置采集到的机械振动信号、驱动电机电流信号,通过进行信号处理提取信号的时域、频域特征,从而判断OLTC的机械状态[1-2]。从振动信号中提取设备状态特征的方法很多,常见的振动信号分析方法有小波变换、包络线法、经验模态分解等[3-4]。以上时、频域方法的分析具有一定的局限性[5],只能提取少量的有效信息,研究发现,OLTC振动结构本身是一个非常复杂的非线性动力学系统,且振动信号表现出混沌特性,混沌诊断理论能够很好地分析OLTC的振动信息。目前,混沌理论被逐步应用于电力系统中电缆、配电网和滚动轴承等设备的故障诊断问题[6-8],但在有载调压变压器分接开关故障诊断领域的应用极少。LVQ神经网络是一种优良的分类器,具有较强的适应能力,得到了广泛的应用。但网络中存在严重的初始连接权值敏感问题[9]。

提出一种基于相空间重构-GSA优化LVQ的有载分接开关机械故障诊断方法。根据OLTC振动信号动力学特征,对振动信号进行CEEMD分解,得到一组IMF分量,并通过C-C法计算嵌入维数和延迟时间重构相空间,计算李雅普诺夫指数和关联维数形成向量进行特征描述,通过GSA算法[10]优化LVQ神经网络,解决输出层与竞争层之间连接权值选择困难导致诊断率低的问题,构建GSA-LVQ分类器实现OLTC机械状态识别。

1 利用CEEMD构造一维时间序列

振动信号包含OLTC切换过程中大量机械状态信息。通过模拟浸油式CM型OLTC的三种运行状态(正常切换、开关滑档、电机机构故障),利用粘合于有载分接开关头盖处的YD-37压电式加速度传感器结合PCT8192采集卡进行数据采集,由GD201信号电缆传输至微型计算机进行数据处理以及状态识别。每种运行状态采集了40组数据,OLTC三种振动信号时域波形如图1所示。

图1 三种振动信号

CEEMD是Yeh等[11]在EMD和总体平均经验模态分解(EEMD)[12-13]上优化的基础上提出了的一种信号时频域分析方法。解决了EMD方法严重的模态混叠现象,同时也克服了EEMD因添加单个白噪声带来的重构误差问题。具体的分解步骤如下:

(1)将一对白噪声分别添加到原始三种振动信号(正常切换、开关滑档、电机机构故障)。为了提取OLTC振动信号的特征,使用CEEMD对原始振动信号Xi(t)添加成对的白噪声mi(t),得到两种不同的新信号Pi(t)和Ni(t)。

Pi=x(t)+mi(t)

(1)

Ni=x(t)-mi(t)

(2)

(2)对这两种不同的新信号分别进行EMD分解,得到j个IMF分量cj(t)=d。

(3)

(3)重复上述步骤,每次加入新的正态分布白噪声序列,并将每次得到的IMF作为最终结果。

以正常切换振动信号为例,对其进行CEEMD分解,得到6阶不同特征尺度的IMF分量,每阶本征模态分量是振动信号分解后按照频率排列,包含了振动信息不同时间特征尺度大小的成分,能够将机械系统中的混沌系统信息蕴含在其中,如图2所示。

图2 不同频率振动信号的CEEMD分解

2 相空间重构的理论与方法

2.1 重构相空间

在OLTC这个非线性振动系统操动过程中,相空间重构能够保持原非线性动力系统的几何不变性[14],采集到的振动信号表现为振动幅值随时间的演变序列,单变量的时间序列中隐含着设备的状态信息,该序列是分析OLTC特征的重要信息源。经CEEMD分解得到的固有模态函数序列是在时间域上的序列,相空间重构就是对混沌时间序列进行处理,从时间序列中提取到更多OLTC的状态信息。文中应用延迟坐标法[15],选取任意一个IMF分量时间序列{Yi(t)}经不同延时构造状态向量,重构相空间可由式(6)表示:

(4)

x(k)=x(t+kΔt),k=1,2,…N

(5)

(6)

式中x(k)为k时刻离散化的系统值;τ为延迟时间;m为嵌入维数;t为采样开始时刻;Δt为采样间隔;N为采样长度。

重构相空间的过程中尤为重要的是选取延迟时间和嵌入维数这两个参数。

2.2 确定延迟时间和嵌入维数

在前人研究的基础之上,文中认为二者是相关联的[16-17],并采用C-C算法对延迟时间和嵌入维数进行联合计算,和其他算法相比,此算法融合了自相关和互相关算法的优点,计算量小、操作容易易实现,在求解分线性模型方面有着较大优势[18],计算步骤如下:

(1)根据延迟时间τ的不同,将振动信号的每阶固有模态分量序列{Yi(t)}划分为τ个不相交的时间序列S(m,N,r,τ)。

(7)

(8)

M=N-(m-1)τ

(9)

(10)

(11)

式中dij为∞函数;r为搜索半径,取小于max(dij)的任意值;θ(x)为Heaviside函数;C(m,N,r,τ)为嵌入时间序列的关联积分;

(12)

(13)

(14)

(15)

式中nm为m个可能的取值;nk为k个可能的取值。

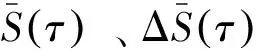
(16)

图3 OLTC固有模态分量序列的S mean曲线、delt S mean曲线和S scor曲线

因重构相空间的冗余和奇异吸引子轨道拥挤程度会因这两个重要参数的改变而改变,所以C-C算法得到的延迟时间和嵌入维数即为最优值。

3 混沌运动的特征提取

在实际工程应用中,存在潜在故障的OLTC振动信号会因时域、频域分解长度不同而存在波形相似的情况,而且相空间直观图并不能定量反映非线性系统的本质特征,重构向量空间后需要度量其动力学特性,因此需要引入最大李雅普诺夫指数和关联系数进行特征描述。

关联维数D是判断序列是否具有混沌特性的关键指标。通常由饱和关联维数法(G-P法)进行计算,当邻域半径r趋于零时,所求极限即为关联维数,计算公式如下:

(17)

(18)

(19)

下面以正常切换为例,通过G-P算法[19]求解OLTC固有模态分量序列的关联维数,lnC-lnr曲线关系如图4所示,拟合m=4时所得直线斜率为0.036 6,可认为OLTC振动信号固有模态分量的关联维数D=0.036 6。

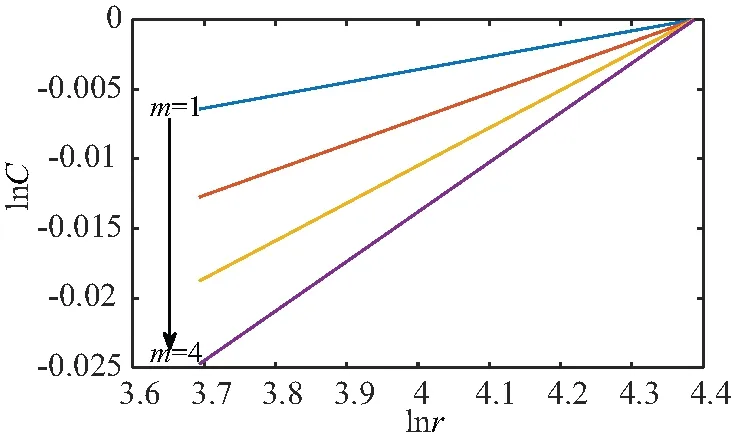
图4 OLTC固有模态分量序列的lnC-lnr曲线

李雅普诺夫指数是用来评价系统的收敛或发散程度的指数。其中最为经典的是Wolf提出的一种求最大李雅普诺夫指数的方法,计算步骤如下:

(1)利用相空间重构技术,对采样点为N的样本序列构造m维相空间新序列, 见式(16);

(2)寻找与初始相点距离最近的点P0(t0),并跟踪测量两点间的距离L0是否大于ε。

L0=|P(t1)-P0(t1)|>ε

(20)

(3)寻找一点与P0(t0)相间夹角最小且距离最近的一点。

L′1=|P(t1)-P1(t1)|<ε

(21)

(4)重复上述步骤,直至迭代所有的序列点,最大李雅普诺夫λ计算公式如下:

(22)

式中T为迭代次数。

根据Wolf提出的求解最大李雅普诺夫指数的方法中式(20)～式(22)可计算相空间的最大李雅普诺夫指数。表1是以正常切换状态下振动信号为例的特征向量:最大李雅普诺夫指数和关联维数。

表1 重构相空间特征

两个指数在混沌力学角度上一定程度地描述了OLTC所有相点在相空间内的分布特性,可将二者提取出来作为重构相空间分布特征T1=[T11,T12,…,T16]和T2=[T21,T22,…,T26]。

将OLTC每种运行状态对应的12维特征量T=[T1,T2]=[T11,T12,…,T16,T21,T22,…,T26]输入神经网络中进行机械状态识别。

4 基于GSA优化的LVQ有载分接开关机械故障诊断

4.1 GSA优化LVQ算法

LVQ神经网络是用于分类的监督学习算法,同时融合了竞争学习特点,是一种最近邻原型分类器。它由输入层、竞争层和线性输入这三层神经元构成[20],结构如图5所示。LVQ存在初始权值敏感问题,当初始权值偏差过大,不仅会导致资源浪费,同时较大程度上影响网络的诊断速度和识别效果。

图5 LVQ网络结构示意图

采用全局搜索能力较强的GSA算法对LVQ的竞争层网络权值wii(12×16个权值向量)进行全局寻优。将粒子编码赋给网络权值,通过牛顿第二定律进行迭代,寻找粒子的最优位置。构造一个输入R=12维特征,输出S2=3维二值向量的LVQ网络,在训练过程中通过GSA算法对粒子适应度的不断更新,实现对LVQ网络初始权值的不断调整。

LVQ网络权值优化过程具体如下:

(1)创建LVQ网络,初始化网络权值wij,形成n个随机初始化粒子位置编码。

(23)

(2)计算初始粒子适应度,采用均方误差最小作为万有引力算法寻优的适应度函数。

(24)

式中N为样本数;wj为实际输出值;wi为期望值。

(3)计算t时刻粒子j对i的万有引力。

(25)

(26)

(27)

(28)

(29)

(30)

式中randj为0～1之间的随机数。

(5)判断循环是否终止。当迭代次数大于设定最大迭代次数,则寻优终止,反之,返回步骤(2)。

(6)按照上述步骤,训练模型已经生成,接下来可将测试数据输入模型即可完成状态诊断。

4.2 有载分接开关故障诊断

采用GSA-LVQ的有载分接开关诊断流程图如图 6所示。

将90组用于网络训练,30组用于测试诊断算法正确率,基于GSA-LVQ的OLTC故障诊断结果如图7所示,图中纵坐标的数字对应OLTC三种机械状态(1:正常切换;2:开关滑档;3:电机机构故障)。由诊断结果可知GSA-LVQ根据描述动力系统特征量进行状态识别的正确率达96.6667%,可靠性较好。对比GSA-LVQ与LVQ算法诊断结果如表2所示,相比之下优化后的算法大大缩短了寻优时间,诊断正确率有所提高,说明提出的GSA-LVQ是有效的,可在一定程度上弥补LVQ对初始权值敏感的缺陷。

表2 不同算法诊断时间和分类准确率

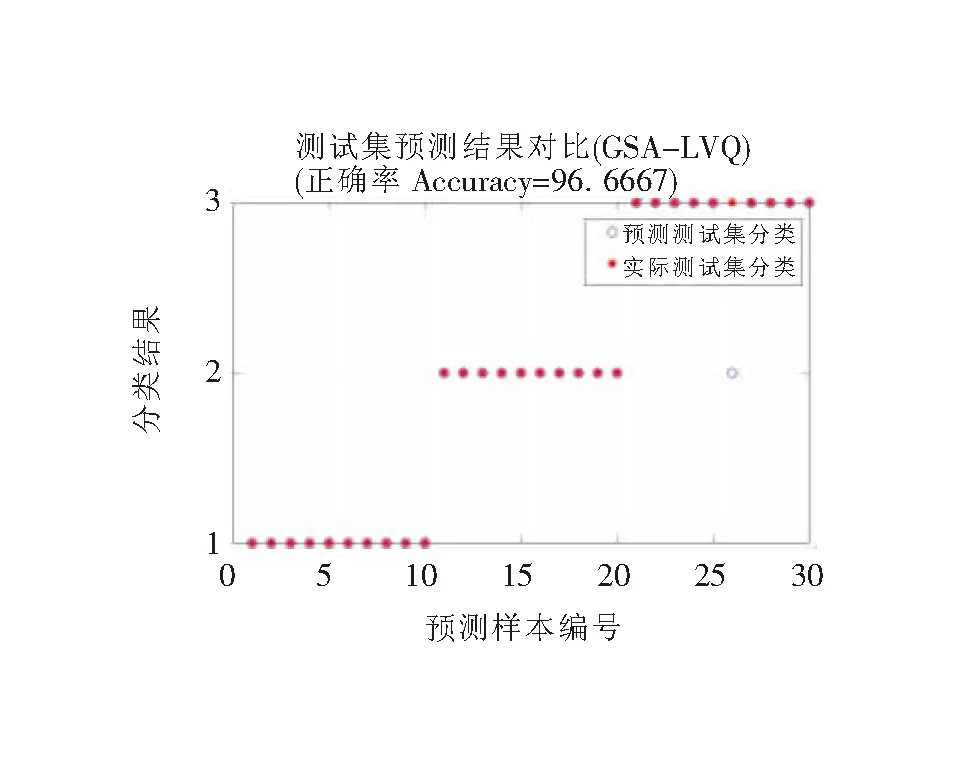
图7 GSA-LVQ神经网络诊断结果

5 结束语

提出基于CEEMD、相空间重构和GSA-LVQ的有载分接开关的振动信号分析及机械故障状态识别算法,检测OLTC机械故障准确率较高。通过CEEMD分析得到的IMFs分量,从混沌动力学分析角度引入重构相空间,弥补了传统时频域方法分析OLTC振动信号的缺陷;实验证明,由GSA优化LVQ神经网络算法在诊断时间、准确率方面都有所提升,一定程度上克服了自身对初始权值敏感的问题,增强了学习效率和网络性能。