新型电力系统主变压器谐波损耗预警方法

齐立忠,张苏,武宏波,许方荣

(国网经济技术研究院有限公司,北京102209)

0 引 言

现阶段,电力系统正处于突飞猛进的发展阶段,新型电子设备的接入在提高电力系统性能的同时,也产生了不计其数的谐波污染。主变压器是电网中连接各种电压等级网络的主要设备,其稳定可靠地运行是保障整个电网运行的关键。结果显示,若主变压器长时间处于谐波环境中,极易导致出现内部温度异常升高、损耗增长速度加快等问题。根据相关统计数据,在整个电力系统中,主变压器由于谐波损耗所引起的电力消耗约为0.06%左右,长此以往,对电力系统造成的损失将是无法估量的。由此可知,新型电力系统是未来的大趋势,它不仅推动持续发展理念,且具有安全可控智能友好等特征。所以,对新型电力系统中主变压器进行谐波损耗的计算与预警具有重要意义。

部分学者对变压器谐波损耗展开相关研究。文献[1]在有限元理论的基础上,利用2D和3D模型匹配的方法对变压器谐波损耗进行计算。分析变压器内部的损耗情况,确定杂散损耗位置,针对不同谐波损耗选择相应的计算方法。文献[2]对Bertotti损耗模型作出部分改进,完成对变压器谐波损耗值的计算。分析变压器当前实际运行情况,利用数值拟合法得到Bertotti损耗模型;考虑谐波相位、含量等因素,在Bertotti损耗模型中引入修正因子,修正模型后直接进行谐波损耗值的计算。文献[3]分析高次谐波作用下的集肤效应和邻近效应对绕组电磁场的影响,利用坡印亭矢量法,建立变压器高次谐波损耗计算模型,实现谐波损耗的计算。文献[4]提出一种用于模块化多电平转换器的功率损耗优化控制,向模块化多电平转换器的循环电流中注入最佳二阶谐波电流,降低每个子模块的底部开关/二极管的最大功率损耗。

上述方法并未考虑到谐波损耗值过大对变压器产生的实际影响,基于此,文中提出基于建筑信息模型(Building Information Modeling,BIM)全寿命周期的主变压器谐波损耗预警方法。首先,对主变压器谐波损耗进行计算,得到精准的谐波损耗值;然后,分析影响主变压器谐波损耗的各项因素,根据国家相关标准设定预警值;最后,将计算得到的谐波损耗值与预警值进行对比,若达到预警值则发出相应的报警提醒。在对比实验测试中,文中方法取得的谐波损耗值最接近实际值,因此,发出的预警提醒可信度最高。

1 基于BIM全寿命周期的主变压器谐波损耗计算

BIM是一种将设备的管理与分析过程以数字化的方式表达出来的模型,能够在施工过程中进行交互和信息交换。基于BIM技术的多方优势,能够实现多方协同设计、参数化设计、项目生命周期信息的整合。文中将其应用在主变压器谐波损耗预警中,通过分析主变压器实时运行情况,进行动态跟踪与管理,来提高算法整体的计算效率和预警效率。

在对主变压器的各项性能分析过程中,必须要考虑到在BIM全寿命周期内不同阶段的实际变压器与理想变压器间差异性。为了降低这种差异性,文中引入了等效电路法。等效电路法原理如下:

首先,对主变压器进行了开路实验,得出了Rm+Xm的励磁阻抗;然后,进行了主变压器的短路实验,得出了一次侧电阻R1+X1和二次侧电阻R12+X12的等价串联阻抗。图1展示了主变压器T形等效电路图。

图1 主变压器T形等效电路图

1.1 铁芯谐波损耗分析与计算

主变压器铁心谐波损耗本质上是一种不受主变压器负载影响的励磁损耗[5-6]。磁滞损耗是由于铁芯长时间的磁化形成的,基于BIM可知损耗的大小与其内部晶体的纯度及形变程度有关。参考斯坦梅茨经验公式,对主变压器磁滞损耗PB进行推理,表达式如式(1)所示:

(1)

式中KB是一个常数项,其值受铁芯尺寸大小和材料影响;f表示铁磁的磁化频率;Bmax表示主变压器铁芯磁通密度;η表示磁滞系数[7],取值范围在2.0～3.5之间,与铁芯材料有关。

又因为:

(2)

式中V表示理想状态下的主变压器电压有效值;N表示主变压器绕组总匝数;A表示测量过程中,铁芯有效面积大小。

通过分析式(1)和式(2)可知:

(3)

在谐波环境下,计算铁芯磁滞损耗值,公式如式(4)所示:

(4)

式中Pn表示在第n次谐波作用下,铁芯磁滞现象产生的损耗值;Vn表示第n次谐波后,主变压器电压有效值;fn表示在第n次谐波条件下,主变压器的磁化频率[8-11]。

通过对主变压器硅钢片的电磁场进行麦克斯韦方程分析,得出硅钢片中电磁场的分布情况,并在第n次谐波作用下,计算铁芯涡流损耗Pn为:

(5)

式中φnm表示主变压器磁通幅值;l、d、h分别表示硅钢片的长度、厚度以及高度;γ代表了电导率。

在不同阶次的谐波环境下,通过叠加计算[12-15]的方式得到主变压器硅钢片涡流损耗,计算公式如式(6)所示:

(6)

由此一来,确定各项参数后,即可通过式(6)推理得到铁芯谐波损耗值。

1.2 绕组谐波损耗分析与计算

主变压器绕组谐波损耗的主要影响有直流损耗P(I2R)、涡流损耗PEC-R以及杂散损耗[16-18]POSL-R。在高次谐波情况下,为了获得精确的谐波损耗,必须将邻近效应和集肤效应等多重影响因子综合考虑在内。

在IEEE/ANSI C57.110标准的约束下,引入谐波损耗因子分别对P(I2R)、PEC-R和POSL-R进行计算,得到谐波条件下,主变压器绕组谐波损耗总值,计算公式为:

(7)

式中Rdc表示主变压器直流电阻;FHL、FHL-STR分别表示涡流谐波损耗因子[19]和杂散谐波损耗因子。对FHL和FHL-STR的定义公式如下所示:

(8)

(9)

一般情况下,必须利用主变压器的测试电阻才能计算得到PEC-R和POSL-R的具体值,但测试环境下主变压器很难体现出真正的运行状态。因此,基于新型电力系统主变压器运行全寿命周期,只考虑式(7)中的直流电阻损耗,那么,式(7)改写为:

(10)

式中K表示主变压器谐波损耗系数值。有研究表明,主变压器PEC-R和POSL-R约占绕组总损耗的20%～30%左右(数据根据GB/T 22072-2008标准分析得到),进而推理出K的值约为1.26。

当前,主变压器绕组谐波电阻模型[20-21]直接被认定是直流电阻的S倍,不考虑邻近效应和集肤效应的影响,当电流中出现较高次的谐波时,计算结果将出现较大的偏差。为了降低这种偏差,文中利用式(11)对Rdc作出了修正:

Rdc=Rt(c0+c1nb+c2n2)

(11)

式中Rt表示基波频率下主变压器的直流电阻;b代表的是幂;c0、c1、c2代表的都是多项式系数[22],且各项系数之间满足条件c0+c1+c2=1,文中汇总了4个系数的大致取值范围,具体如表1所示。

表1 多项式系数取值范围

综上所述,主变压器绕组谐波损耗计算公式整理为:

(12)

通过式(12)可以得出结论,对主变压器绕组谐波损耗值影响最大的影响因子是二次侧谐波电流。

2 主变压器谐波损耗预警

通过图1和上文分析可以发现,主变压器谐波损耗的主要影响因子为谐波次数的变化和负载平衡情况[23]。通过对主变压器进行空载和短路试验,得到主变压器谐波模型参数,具体如表2所示。

表2 主变压器谐波损耗模型参数

xn(1)、xn(2)和xn(m)为直流电阻损耗值,rn(1)、rn(2)和rn(m)为直流电阻修正值。根据表2中数据可知,修正后的直流电阻值有效减小,主变压器谐波损耗随之减小。在三相负荷均衡、功率恒定的条件下,即三相电压源输出波形是正弦波,且频率相同,幅度相同,功率恒为谐波损耗功率的10%以下。根据表2直流电阻修正值,调整各次谐波含有率[24-25],可以使主变压器的谐波电流发生变化,由此得出主变压器的谐波次数与谐波损耗之间的关系,如图2所示。

图2 主变压器谐波次数与谐波损耗关系图

由图2可知,当谐波含有率恒定时,谐波次数的增加带动主变压器谐波损耗值的增加,且二者之间变化趋势成正比关系。参考国家相关标准,当主变压器谐波损耗占总电量的10%以下为正常范围,无需发出任何报警提醒,一旦谐波损耗值超出了这个范围则会发出相应的报警。

3 实验测试

为了验证文中方法在实际应用中是否具有同样合理有效,与引言中提到的有限元理论和改进Bertotti损耗模型进行了对比实验测试。

3.1 实验条件

实验在某变压器厂展开,主变压器谐波损耗检测与分析平台如图3和图4所示。采用电力变压器调节直流电阻,控制主变压器谐波,实现主变压器谐波损耗检测。通过示波器观察电源输出波形,功率分析仪可以检测功率消耗,使功率保持恒定。温度巡检仪防止谐波损耗过高,温度升高发生危险。

图3 主变压器谐波损耗检测实物图

图4 主变压器谐波损耗检测与分析平台

文中以主变压器铭牌参数和主变压器电路模型为基础,采用主变压器谐波损耗分析软件,对其进行了研究并仿真。

仿真过程中主变压器相关参数设置如下:容量1 kV·A-3 000 kV·A、输入电压允许额定电压±10%波动、输出电压负载范围内额定电压±(2%～3%),绝缘电阻DC 500 V≥100 MΩ,空载损耗35 kW,负荷损耗155 kW,空载电流0.81%,阻抗电压10.3%。

仿真软硬件结构参数如下:系统软件采用Visual C++ 6.0开发,包括: 数据显示模块、串口操作模块和变压器参数设置模块。系统硬件主控制器为CS3000,实现模拟量检测,并通过串口与上位机通信,为监测变压器谐波附加损耗提供实时数据。

3.2 实验分析

(1)实验过程

文中在上述实验环境和参数设置下,进行如下实验:

实验1:采集终端谐波损耗值:采用了主变压器谐波损耗采集终端,对两种不同负载下的谐波损耗进行了测量,对比三种算法和采集终端谐波损耗值;

实验2:在谐波含有率分别为1%、3%、5%、7%、9%、11%、13%、15%的情况下进行测试,观察谐波损耗占比变化,及与预警值的对比结果;

实验3:对磁通密度值(单位:T)为0.1、0.2、0.3、0.4、0.5、0.6分别进行测量和计算谐波损耗,得出误差范围。

(2)实验结果

实验时,采用钳形电流互感器,使其与变压器的原、副端相接触,引入文中方法、有限元理论和改进Bertotti损耗模型对谐波损耗值进行计算,并在此基础上,采用了主变压器谐波损耗采集终端,对两种不同负载下的谐波损耗进行了测量,比较4个数据,结果如图5所示。

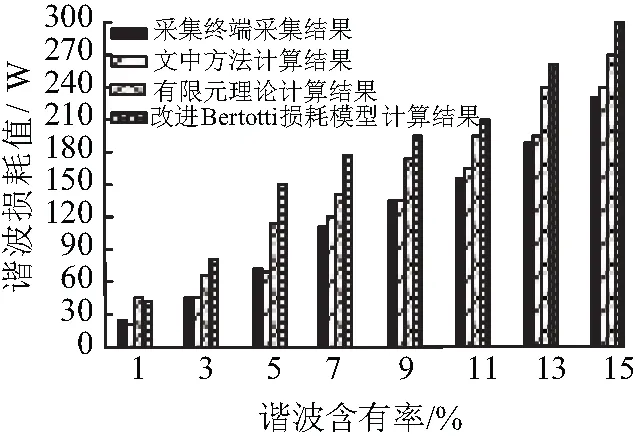
图5 三种算法与采集终端谐波损耗值对比

从图5中可以看出,谐波含有率为15%时,采集终端230,有限元理论计算结果为270,改进Bertotti损耗模型计算结果为300,利用文中计算方法结果为240,有限元理论和改进Bertotti损耗模型与采集终端获得到的谐波损耗相差越来越大,只有文中方法计算得到的谐波损耗始终接近于采集终端结果。由此可以得出结论,无论谐波含有率如何变化,文中方法都能取得最精准的主变压器谐波损耗值,并与预警值达到最精准对比,得出谐波含有率、谐波损耗值与预警值间的准确数据及联系。

实验中,将流经主变压器的总电流设置为1 800 A,参考国家相关标准,谐波损耗占比不超过10%无需发出任何预警。将图5文中算法取得的谐波损耗值与预警值进行对比,结果如图6所示。观察图5中谐波含有率分别为1%、3%、5%、7%、9%、11%、13%、15%的情况,文中方法计算得到的主变压器谐波损耗值分别为25 W、45 W、63 W、120 W、135 W、169 W、194 W、240 W。

图6 文中方法谐波损耗值与预警值对比结果

参考国家相关标准,当新型电力系统主变压器谐波损耗占总电量的10%以下为正常范围,无需发出任何报警提醒,一旦谐波损耗值超出了这个范围则会发出相应的报警。由图6可知,当谐波含有率为13%和15%时,文中方法计算得到的主变压器谐波损耗值占比高出总电流10%以上,需要发出报警提醒。而在谐波含有率分别为1%、3%、5%、7%、9%、11%时,谐波损耗值均未超过10%预警值,因此不需要发出报警提醒。

利用文中方法对测试的主变压器谐波损耗进行计算,并与测量值对比,结果具体如表3及表4所示。

表4 谐波损耗计算结果验证

通过分析表3和表4,在不同磁通密度值下,文中计算得到的损耗值变化趋势与测量值一致,均随着磁通密度的增大而上升。且文中方法的损耗计算值与测量值差距较小,误差始终保持在5%以内。

结合上述实验结果可知,主变压器谐波损耗的主要影响因子是谐波含有率、磁通密度值,当谐波含有率恒定时,谐波次数的增加带动主变压器谐波损耗值的增加,且二者之间变化趋势成正比趋势,当谐波含有率增加时,谐波损耗值随之增加;谐波损耗值随着磁通密度值的增加而增加,直至达到预警值发出报警提醒。

综上分析可知,文中方法可以精准计算得到主变压器的谐波损耗值,进一步推理得到在总电流中的占比情况,与预警值进行对比,对超出预警值的情况及时发出报警提醒。

4 结束语

考虑到谐波损耗对新型电力系统主变压器使用寿命的影响,文中从BIM全寿命周期角度,展开对主变压器谐波损耗预警的研究。在计算了主变压器谐波损耗具体值后,通过分析影响主变压器谐波损耗的各类影响因子,设定符合国家相关标准的预警值,将计算结果与该值进行对比,如若超出该值则发出相应的报警提醒。通过进行对比实验结果,文中方法取得了谐波损耗值精准度最高,从而发出的预警提醒也更加精准。