基于秃鹰搜索算法优化LSTM的短期风速预测
李诗洋,刘闯
(国网湖北省电力有限公司荆门供电公司,湖北 荆门 448000)
0 引 言
随着温室效应的加剧,煤、石油等化石能源的不断开发,传统能源正在走向枯竭,寻找化石能源的替代品已迫在眉睫[1]。风是一种可再生能源,具有广阔的开发前景,但风速变化具有很大的间歇性和随机性,导致风电并网会给电力系统造成很大冲击[2-3]。因此,研究风速的变化规律,准确预测风速,对于提高风电利用率、减少化石能源消耗和降低发电成本,具有深远意义。
针对短期风速预测,国内外专家进行了大量研究,并基于统计法和物理法提出了一些短期风速预测方法,但由于风速变化的规律性很弱,导致这些方法的预测精度并不高[4-5]。随着人工智能的推广,许多基于智能算法的短期预测方法被提出来。文献[6]首先采用变分模态分解法(variational mode decomposition,VMD)对原始风速序列进行分解,然后采用改进食肉植物算法(improved carnivorous plants algorithm,ICPA)优化最小二乘支持向量机(least squares support vector machine,LSSVM)的参数,建立了基于VMD-ICPA-LSSVM的短期风速预测模型,最后对模型进行误差修正,提出了一种短期风速组合预测方法。文献[7]对原始风速数据进行VMD分解,采用改进粒子群算法(improved particle swarm optimization,IPSO)对LSSVM的两个参数进行优化,提出了一种新型短期风速预测方法。文献[8]为了解决BP神经网络选取不当的问题,采用麻雀搜索算法(sparrow search algorithm,SSA)对BP神经网络参数进行优化,提出了一种基于SSA算法优化BP神经网络的短期风速预测方法。研究表明,风速受风向、温度和气压等因素的影响较大[9],现有风速预测方法更注重与对风速数据内部规律的挖掘,而忽略了其影响因素的作用。
基于此,本文以风速、风向、温度和气压为特征量,采用秃鹰搜索算法(bald eagle search,BES)寻找长短时记忆神经网络(long short term memory,LSTM)的最优超参数,建立基于BES-LSTM短期风速预测模型,采用实际风速监测数据对模型的正确性和有效性进行验证。
1 长短时记忆神经网络
LSTM是在递归神经网络的基础上通过改进得到的[10],它在循环神经网络(recurrent neural network,RNN)上增加了三个门控单元,分别是输入门、遗忘门、输出门。输入门用于读取输入数据。遗忘门的作用是筛选并保留重要数据信息,并阻断无用信息的传递。输出门负责将处理过的数据继续向后传递。门控单元解决了RNN在训练过程中的爆炸缺陷和梯度消失问题。LSTM具有独特的记忆单元和门控单元,这些单元能够有效处理长时间数据序列,解决了传统神经网络依赖输入序列的问题,图1所示为LSTM的结构单元,LSTM的计算原理可参考文献[10]。
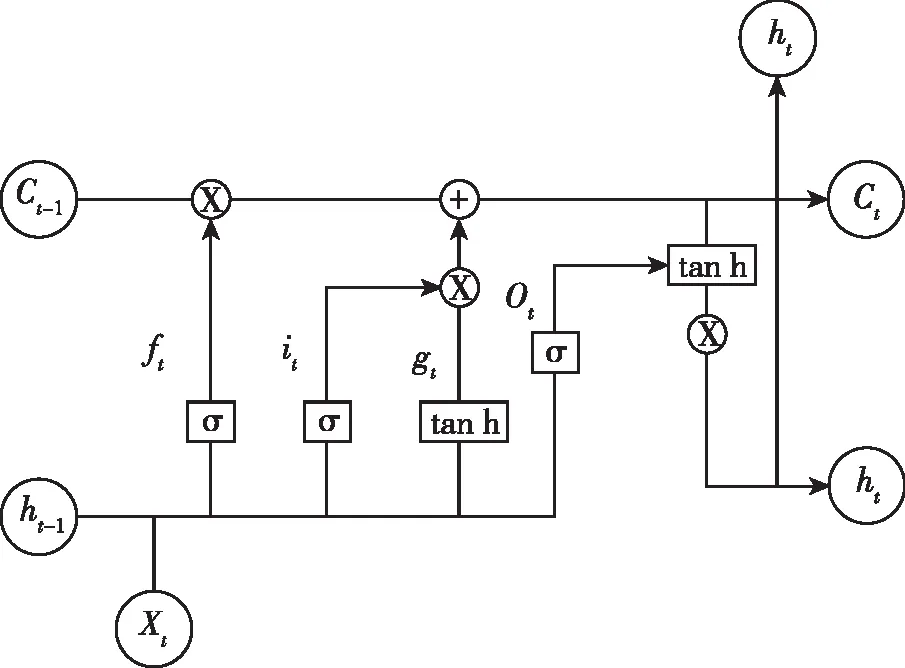
图1 LSTM结构单元。
2 秃鹰搜索算法
2.1 BES算法基本原理
BES算法由马来西亚数学家 H.A.Alsattar[11]提出,其基本原理是对自然界中秃鹰捕食猎物过程的模拟。BES算法的寻优主要分为选择搜索空间、搜索猎物和俯冲3个阶段。经过3个阶段,秃鹰种群逐渐向猎物靠拢,最终捕获猎物,即算法找到全局最优解在整个寻优过程中,秃鹰的运动轨迹始终围绕一个中心点,并以该点为基础展开搜索,BES算法的优化原理可参考文献[11]。
2.2 BES算法性能测试
相比粒子群算法[12](particle swarm optimization,PSO)和遗传算法[13](genetic algorithm,GA)等传统优化算法,BES算法的鲁棒性好,全局搜索性能更强。为此,采用表1中的三个测试函数对BES算法、PSO算法和GA算法的优化性能进行验证。在表1中,函数f1、f2和f3分别为多维单峰函数、多维多峰函数和低维多峰函数,利用这些函数可以对算法的全局搜索性能和局部优化性能进行充分测试。
设测试函数的空间维度均为30,BES算法、PSO算法和GA算法的种群容量均为30,最大迭代次数均为500。利用三种优化算法分别对测试函数进行30次寻优,三种算法的平均收敛曲线如图2所示。
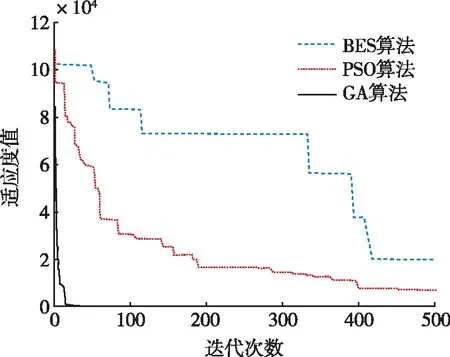
(a)函数f1。
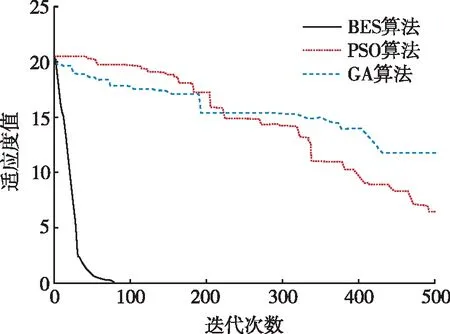
(b)函数f2。
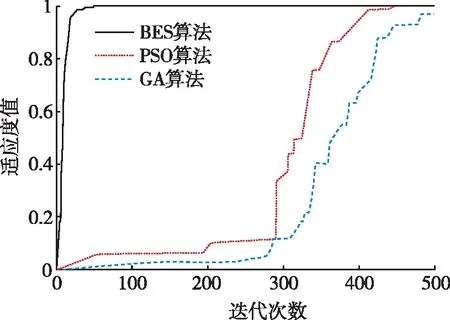
(c)函数f3图2 收敛曲线对比。
对比图2可知,相比PSO算法和GA算法,BES算法的收敛时的迭代次数更少,优化函数f1、f2时的最小适应度值更优,优化函数f3时的最大适应度值更优,具有更高的收敛精度。
3 基于BES-LSTM的短期风速预测模型
研究表明,风速变化具有混沌时间特性且受到风向、气压和温度等气象因素的影响[14]。LSTM的训练效果受其隐含层单元数量、正则化系数和初始学习率三个超参数的影响较大,为了提高LSTM的学习能力,提高短期风速预测精度,采用BES算法对LSTM的三个超参数进行寻优,建立基于BES-LSTM的短期风速预测模型,图3所示为BES-LSTM模型的流程,主要建模步骤如下:
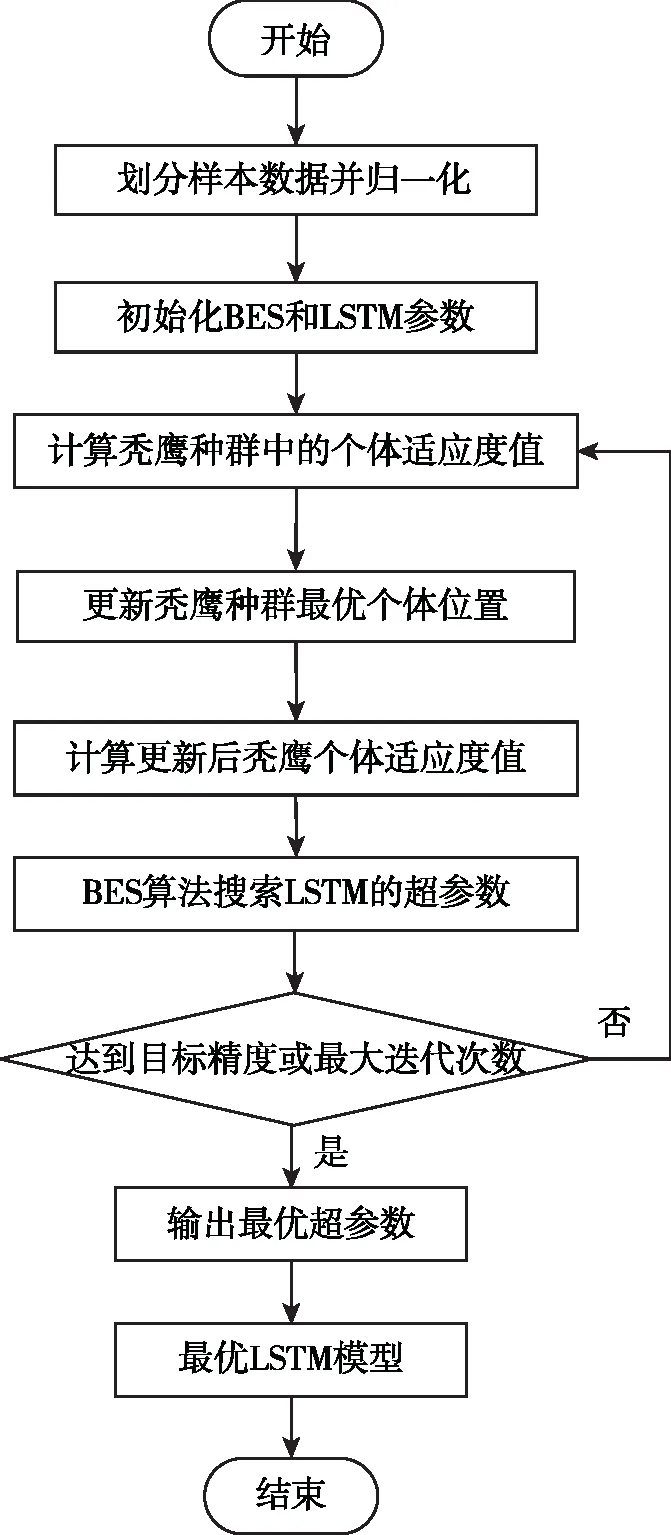
图3 BES-LSTM模型流程。
1)确定训练样本。考虑到风速变化的时间特性及气象因素的影响,将前3个时刻的风速和当前时刻的气象因素作为短期风速的特征量,具体如下:
vt=f(vt-1,vt-2,vt-3,dvt,pt,Tt)
(1)
式中:vt、vt-1、vt-2和vt-3为当前时刻、t-1时刻、t-2时刻和t-3时刻风速,dv、pt和Tt为当前时刻风向、气压和温度。

表1 测试函数
2)划分训练样本并归一化。将样本数据划分为训练集和测试集,并全部归一化,公式如下:
(2)

3)初始化BES算法的相关参数,设置秃鹰种群容量为30,最大迭代次数均为500。构建LSTM短期风速预测模型,随机生成一个秃鹰种群,将LSTM的隐含层单元数量、正则化系数和初始学习率组成BES算法的优化目标,确定各参数的寻优范围。
4)选择搜索空间。利用式(9)更新秃鹰位置并计算适应度值,适应度值的计算公式为

(3)
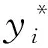
5)搜索猎物,并更新秃鹰位置,计算秃鹰个体适应度值并确定当前最优位置。
6)俯冲抓捕猎物,并更新种群位置,通过比较适应度值优劣确定当前最优解。
7)判断LSTM的输出结果是否满足精度要求或者算法已经达到最大迭代次数,若是则输出最优超参数,否则,返回步骤(4)。
8)将最优超参数赋给LSTM,对测试集进行短期风速预测。
4 仿真分析
采用某风电场连续5天的风速数据和气象数据组成训练样本进行仿真分析,数据采样频率为10 min/次,在连续的时间序列上共选取了600组样本数据。根据建模需要,将600组样本数据划分为训练集和测试集,其样本容量分别为540组和60组,其中测试集部分样本数据如表2所示。
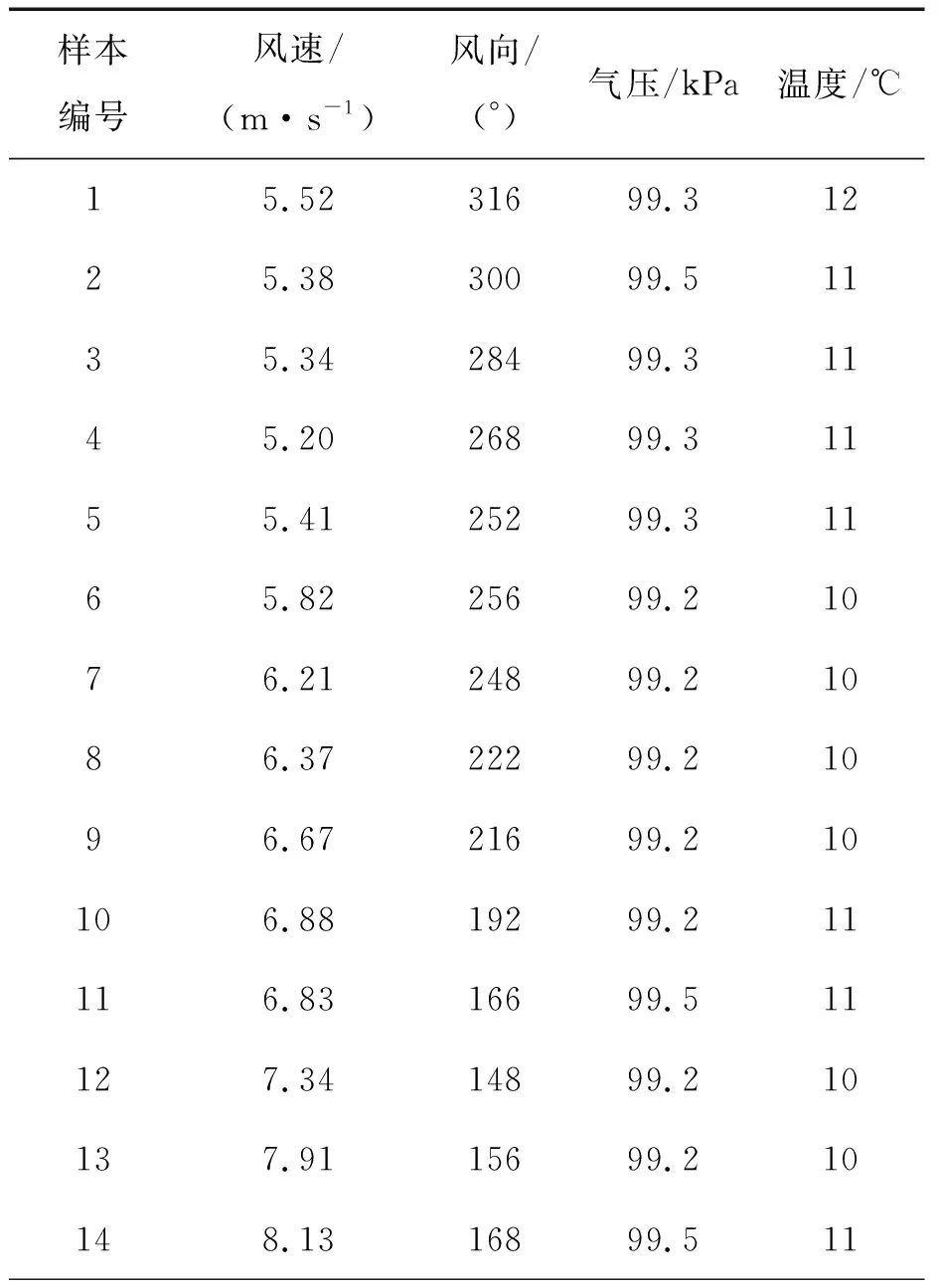
表2 测试集部分样本数据

表2(续)
根据式(1)确定模型输入量,进行仿真分析,利用训练集中的540组样本数据进行训练,采用BES算法对LSTM的隐含层单元数量、正则化系数和初始学习率三个超参数进行优化,BES算法的寻优结果如表3所示。

表3 BES算法的寻优结果
将三个超参数的寻优结果赋给LSTM,利用BES-LSTM模型对测试集中60组样本数据的风速进行预测。为了对比分析,采用文献[15]中的PSO-LSSVM短期风速模型和文献[16]中的SSA-ELM短期风速预测模型对测试集样本进行预测,BES-LSTM模型、PSO-LSSVM模型和SSA-ELM模型的风速预测结果及绝对误差如图4和图5所示,对比图4和图5中的数据可知,BES-LSTM模型的预测结果更接近实际值,绝对误差波动更小。
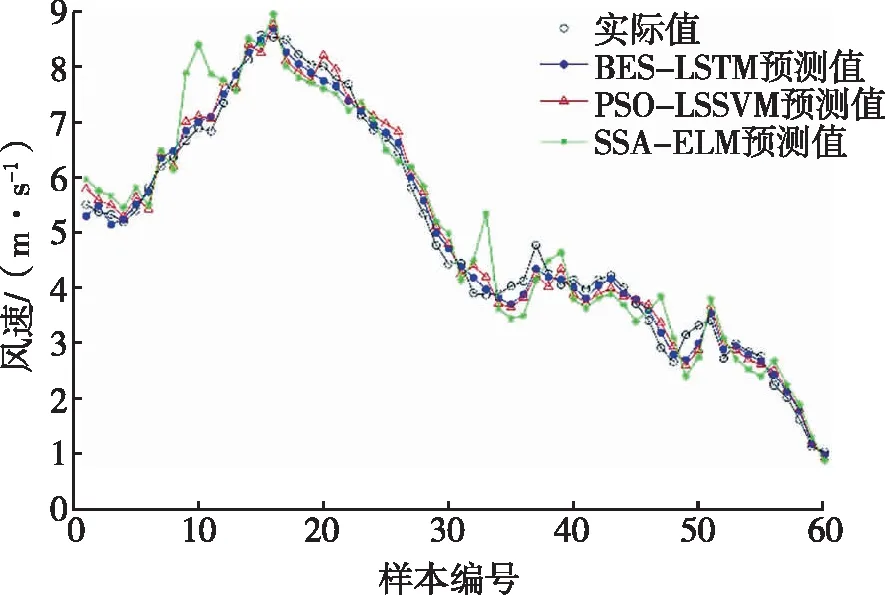
图4 风速预测结果。
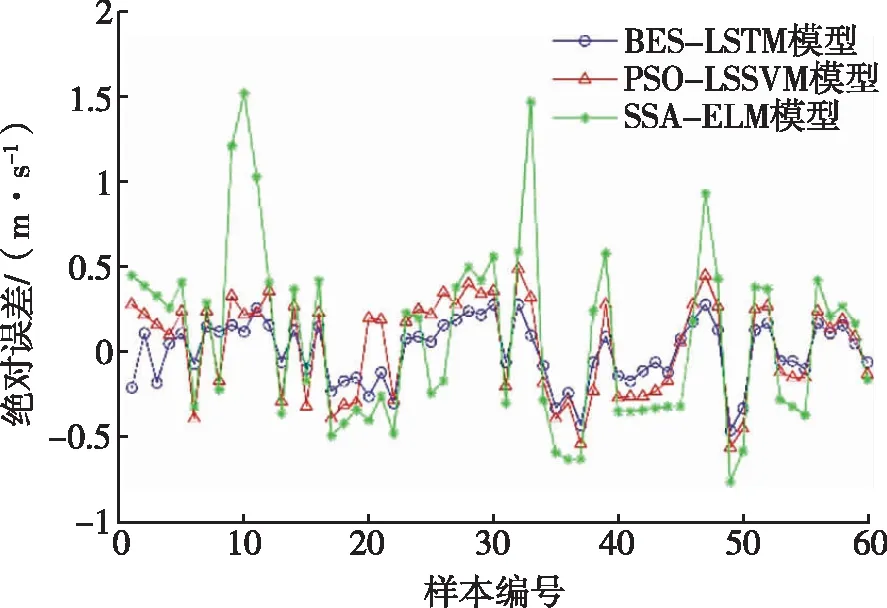
图5 各模型预测结果的绝对误差。
为了对三种风速预测模型的预测效果进行综合评价,采用方均根误差、平均相对误差和可决系数三种指标对短期风速预测结果进行评价,它们的计算公式依次为
(23)
(24)

(25)

三种模型预测结果的误差指标如表4所示。由表4可知,BES-LSTM模型预测结果的方均根误差、平均相对误差和可决系数分别为0.182、3.742%和0.992,各项指标均优于PSO-LSSVM模型和SSA-ELM模型,可见基于BES-LSTM的短期风速预测方法的预测效果更好,具有一定的工程推广意义。
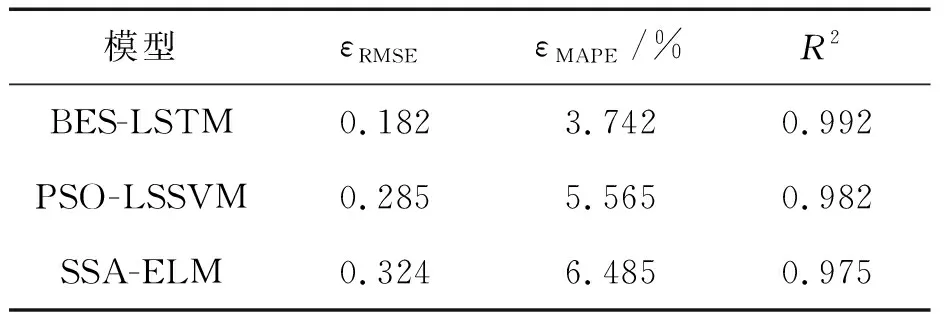
表4 三种模型预测结果的误差指标
5 结 论
本文考虑了风速时间特性及气象因素对风速的影响,选取过去时刻风速和气象因素作为短期风速的特征量,采用BES算法对LSTM的隐含层单元数量、正则化系数和初始学习率三个超参数进行优化,建立基于BES-LSTM的短期风速预测模型。采用实际风电场相关数据进行仿真分析,并与其他风速预测方法进行对比,结果表明,本文所提BES-LSTM模型在进行短期风速预测时的拟合程度更高、波动性更小、预测精度更高,验证了本文短期风速预测方法的正确性和有效性。

