“结构化视角”下的小学数学作业设计探究

华清波(浙江省杭州市富阳区富春第五小学 311400)

所谓“结构化”,是将学过的知识逐渐积累再进行归纳与整理,从而形成比较条理化、纲领化的框架,实现纲举目张。心理学研究表明,不同学生在组织知识结构过程中存在明显差异,组织知识结构的过程是呈现螺旋状逐渐上升变化的,而不是简单堆积形成的。对于优秀学生来说,可能是一种有组织、有系统性结构的由易到难、由简单到复杂的层次排列;而对于后进生往往是简单的平行排列,是零散和孤立的,是栅栏状的。

一、新课程标准提出的作业设计要求

常规的小学数学教学在作业设计和作业布置中主要存在两种情况:一种情况是教师仅依据课本上的单元设计及课时划分情况,对整个教材知识的设计不能全面认知,更不能很好地把握小学阶段整个数学知识螺旋发展的结构,过于重视单一课时的教学内容,影响了数学课程目标的实现;另一种情况是教师缺乏对学生的了解,从而忽视了对学生学习整个过程的关联设计,只是简单从课本或一些资料中摘取相关情景或问题,再简单进行整理,忽视甚至限制了学生创新思维及其数学能力与素养的发展,很难培养学生良好的学习认知习惯和勇于探索的科学精神。

《义务教育数学课程标准(2022年版)》(以下简称“新课标”)对小学数学作业设计也有明确要求,如在关注“四基”“四能”达成的同时,特别关注核心素养的相应表现。不仅要关注学生分析问题、解决问题的能力,还要关注学生发现问题、提出问题的能力。若要真正实现以上要求,落实新课程标准要求,让作业设计实现结构化是非常有必要的。

二、结构化视角下对作业设计的方法和策略

1.作业设计要体现学习方法的结构化

(1)数形结合方法的渗透与应用。数形结合方法是小学阶段数学教学研究中解决问题的重要方法。新课标提出,数感与几何直观是进行数学研究的重要内容,有机将数量关系和图形结合分析研究,“数形结合”可以借助简单的图形、符号和文字所作的示意图,促进学生形象思维和抽象思维的协调发展,逐步培养学生想象力和创新意识。

作业设计:一列火车经过南京长江大桥,大桥长6700 米,这列火车长140 米,火车每分钟行400米,这列火车通过长江大桥需要多少分钟?

研究:火车过桥是指“全车通过”,即从车头上桥直到车尾离桥才算“过桥”,作示意图如图1:

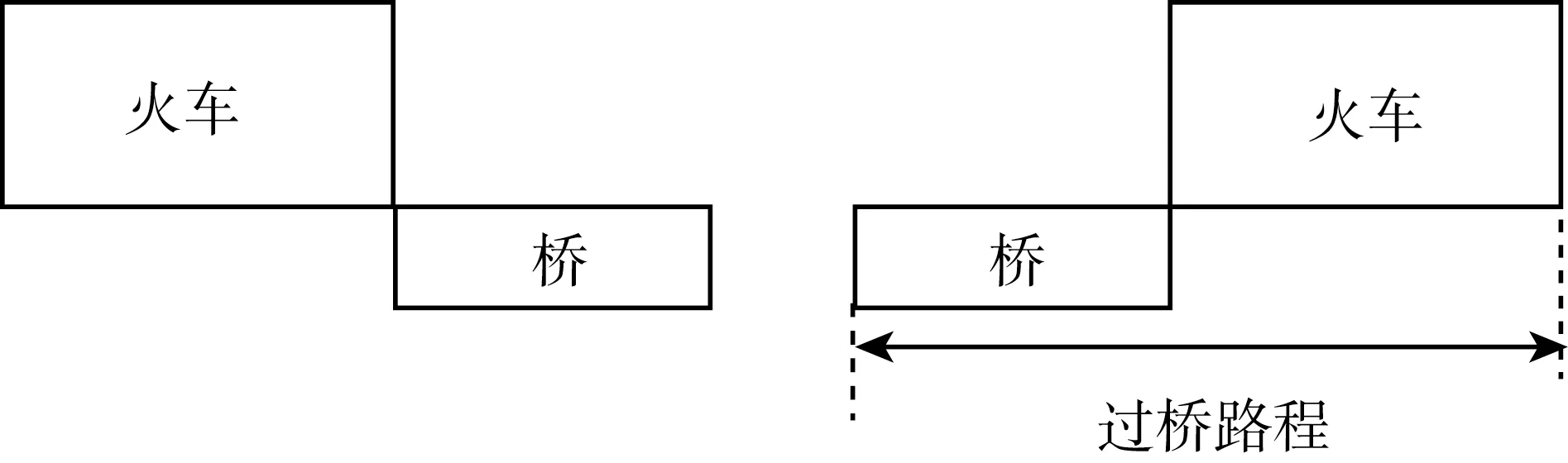
图1

借助基本图形,可以非常清楚地看到火车行驶的总路程(6700+140)米,借助计算得到通过的时间是(6700+140)÷400分钟。

如路程、工程等问题,都可以借助线段图,来具体分析问题情景,通过图形转化简化问题,让学生更容易理解题意,把握解题思路,促进学生数学推理能力发展。

(2)分类讨论方法的体现与研究。在数学问题中,在受某些条件的限制、图形的位置不够确定及其暗含一些字母或者符号不够明确的情况下,我们都要进行分类讨论,这既是一种数学逻辑方法,也是一种数学思想,在解题过程中不但可以简化研究对象,对学生今后思维发展也有重要作用。

作业设计:小明和小英各自在公路上往返于甲、乙两地运动,即到达一地便立即折回向另一地运动。设开始时他们分别从两地相向而行,若在距甲地4000米处他们第一次迎面相遇,第二次迎面相遇的地点在距乙地3000米处,则甲、乙两地距离是多少千米?

研究:要注意引导学生进行审题,并在阅读思考过程中注意细节处理。首先假设开始时小明从甲地,小英从乙地相向而行,判断出两人第一次迎面相遇时行的路程之和等于两地之间的距离,第二次迎面相遇时行的路程之和等于两地之间的距离的3倍,然后分三种情况讨论:①第二次迎面相遇时,小明从乙地返回,小英从甲地返回;②第二次迎面相遇时,小明从乙地返回甲地后再从甲地返回乙地,小英未到达甲地;③第二次迎面相遇时,小明来到达乙地。小英从甲地返回乙地再由乙地返回甲地,求出甲、乙两地距离是多少千米。

解答这样的问题,关键是结合题意突破问题中所有的三种情况,防止漏解。从此题出发,再深入引导学生思考:什么样的题干会出现分类讨论,该怎么讨论,将问题分析透彻,从而正确得到答案。

(3)转化、归纳方法的了解与把握。转化也是常见的一种数学思想方法,将未知问题转化已知问题来解,将较难问题转化为常见较容易的问题来分析研究;归纳则是将一般性的问题转化为简单的特殊的问题进行分析,从中找到其存在的规律和性质。

作业设计:如图2所示,长方形ABCD的长是8cm,则阴影部分的面积是多少平方厘米?

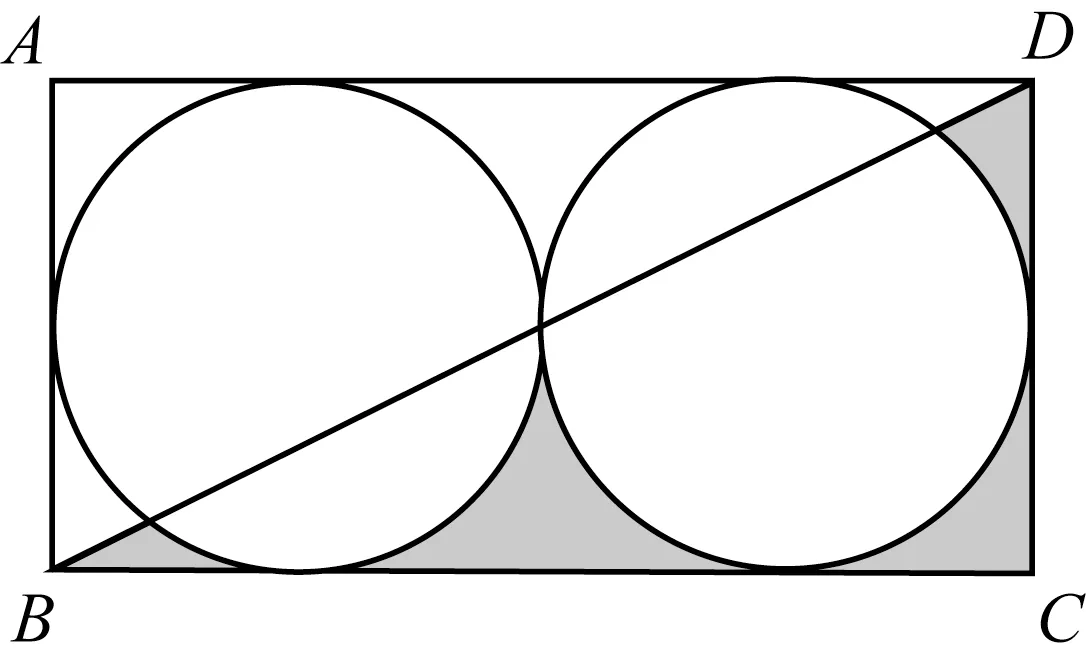
图2

问题中出现的都是不规则图形,小学水平根本就解决不了。但是我们可以进行转化,在直角三角形BCD中两个圆的部分面积之和恰好等于圆的面积,故可以判断得到阴影部分面积等于直角三角形面积-圆面积。

(4)符号、统计方法的认识与渗透。数学知识本身就是与符号分不开的。数学符号的表达,不但有助于学生数学思维发展,更为今后数学从数到式的发展奠定基础,《义务教育数学课程标准(2022年版)》也明确提出要注意符号意识,符号化思想的渗透训练非常必要。

作业设计:a、b、c、d各代表一个不同的非零数字,如果abcd为13的倍数,bcda为11的倍数,cdab为9 的倍数,dabc为7 的倍数,那么abcd是 。

解析:根据上述题意中所述,可以根据11的倍数确定a+c=b+d,再根据a+c+b+d是9的倍数也是偶数的结论,可以判断得到其和是18。

这样,我们根据位值原则,把数字完全拆分,找到a、b、c、d的另一个关系枚举即可得到。

2.作业设计要体现知识过程的结构化

思维教育是数学教学的潜在目的,教师在设计作业时应该将其体现在问题解决过程中。这样才能引导学生将注意力放在探究过程中,让数学问题回归本真。

作业设计:由一些汉字和字母组成如下排列:

杨 庄 中 心 小 学 杨 庄 中 心 小 学 …A B C D A B C D A B C D…

上表中,第一列中“杨”和“A”对应,第二列中“庄”“B”对应……根据上表提示,请说出第2023列的汉字和字母各是什么? (通过计算解决问题)。

这样的问题设计,大多属于规律性探究,直接判断答案不可能,需要我们针对排列,找到汉字和字母之间的内在关系,从而确定答案,过程探究是重点。细细分析,发现第一行汉字是每6 个一循环,第二行字母是4个一循环,这样结合6和4的最小公倍数为12,再用2023去除,余数是几就是第几列的汉字与字母的对应情况。

3.作业设计要体现学生特点的结构化

教师在教学中要根据学生的特点设计个性化的作业,引导学生用不同方式去完成,从而培养学生正确的数学观念,帮助学生养成良好习惯。

(1)分层型作业设计。对不同层面学生设计不同程度的数学作业,可以由易到难,把握基础类的问题,让后进生在作业上能获得成功感,从而产生自信,让优秀学生获得自我突破,让其个性得到发展。根据学生各种表现,依次逐渐增强作业难度,知识点容量也逐步扩大,慢慢形成螺旋状的知识框架,更好激发学生探究内驱力。

(2)开放型作业设计。在教学中,教师要结合教材相关内容探寻生活实践中的相关因素,寻找那些具有代表性、趣味性、时代性极其富有生活特色的情景作为作业情景,再根据相关知识进行构思。如根据小学生的认知情况,将加减法的学习延伸到日常孩子们喜爱的食物、玩具及其游戏中,让学生自主调动自己思维方法进行解答。

作业设计:利用我们学过的“2～6 的乘法口诀”,根据下列情景自行设计购买方案,并自行解答,写出相关过程:2 元/个;火腿肠:1 元/个;巧克力薯片:6元/盒;“营养快线”饮料:4元/瓶;苹果:3元/斤;大雪碧:5元/瓶。

既开放又实践性强的作业设计,直接将学生从学校生活回归到家庭日常生活,让学生体会到现实生活的实际价值,从而感受生活中处处有数学,生活离不开数学。

4.作业设计要体现知识融合的结构化

数学学习离不开其他学科学习,在数学作业设计上要注意渗透其他学科内容,以更好拓宽学生视野,引导学生深入学习,促进学生全面发展。

作业设计:如教学“位置与方向”一课设计一些学生身边比较熟悉的环境,引导学生根据自己认知,也可利用信息技术的模拟功能,创设“学校—回家—游玩”路线图,身临其境真实感受空间位置的变化,从而获得数感、空间观念,促进学生情景化思维培养。

小学数学作业设计历来是一线教师在教学研究领域的焦点问题。当前小学数学教学中,基本是将单元整合与小学数学结构化教学的思路紧密结合在一起,难以从单方面体现全面结构化的数学知识。因此,我们在设计作业时,要注意作业内容与整个单元所体现的数学思想之间的联系,要注意和之后学习相关知识的联系,构成整册、整个阶段的结构化联系,以发展学生思维,增强学生综合实践创新能力。在结构化视角下,合理的作业设计,能够让学生在遇到问题时从多个角度思考,从而激发学习兴趣,提升数学思维能力,培养发散思维。