混杂免疫多目标优化算法及对动态经济环境调度问题优化

唐湘黔 钱淑渠 武慧虹

摘 要：动态经济环境调度（DEED）问题是电力系统调度中一类含大规模约束的高维多目标优化问题，传统的进化算法易于陷入局部最优，使得所获的Pareto前沿分布性和收敛性差。为了充分挖掘免疫系统的克隆选择原理，提出一种混杂免疫多目标优化算法（HIMOA）。该算法以传统进化算法为基本框架，面对高维决策变量优化易于陷入局部最优的缺陷，改进外部存档更新机制以保存历代优秀的多样性个体，采用克隆、高斯突变策略强化局部开采能力，有效地迫使算法跳出停滯搜索状态。为应对大规模约束，提出逐步微调机组出力策略，提高进化群体的可行性。数值仿真实验以10机系统为测试算例，将HIMOA与著名的六种算法MODE、NSGA-Ⅱ、IMOEA/D-CH、ADEA、MOHDE_SAT、MONNDE进行比较分析，结果表明，HIMOA能为DEED问题的10机系统提供较好的Pareto解，所获的Pareto前沿收敛性和分布性优越于其他算法，各评价指标的箱型图表明HIMOA具有优越于其他算法的统计特征。

关键词：动态经济环境调度； 免疫系统； 克隆选择原理； 大规模约束； 多目标优化

中图分类号：TP304.7   文献标志码：A

文章编号：1001-3695（2023）09-024-2720-09

doi：10.19734/j.issn.1001-3695.2023.02.0037

Hybrid immune multi-objective optimization algorithm fordynamic emission economic dispatch

Tang Xiangqian1，2， Qian Shuqu2， Wu Huihong2

（1.College of Mathematics & Statistics， Guizhou University， Guiyang 550025， China; 2.School of Mathematics & Computer Sciences， Anshun University， Anshun Guizhou 561000， China）

Abstract：Dynamic economic emission dispatch（DEED） problem in power system is a kind of high-dimensional multi-objective optimization problem with large-scale constraints. The traditional evolutionary algorithm is easy to fall into local optimization， and the distribution and convergence of the obtained Pareto frontier are poor. This paper fully explored the clonal selection principle of immune system， and proposed a hybrid immune multi-objective optimization algorithm（HIMOA） . The proposed algorithm took the traditional evolutionary algorithm as the basic framework. Since the deficiency of falling local optimization for the high-dimensional decision variables optimization， it improved the external archive update mechanism to preserve the excellent individuals from previous generations， and adopted the cloning and Gaussian mutation strategy to strengthen the local exploitation ability， forcing effectively the HIMOA to jump out of the stagnant search state. In order to cope with the large-scale constraints，it designed the fine-turning output power step by step to improve the feasibility of the evolutionary population. In the numerical simulation experiment， taking a 10-unit system as a test example， and compared HIMOA with the famous algorithms MODE， NSGA-Ⅱ， IMOEA/D-CH， ADEA， MOHDE_SAT， MONNDE. The results show that HIMOA can provide a better Pareto solution to the 10-unit system of the DEED problem， and the convergence and distribution of the Pareto frontier obtained are better than other algorithms. The box diagram of each evaluation metric shows that HIMOA has better statistical characteristics than other algorithms.

Key words：dynamic economic emission dispatch; immune system; clonal selection principle; large-scale constraints; multi-objective optimization

0 引言

动态经济调度（dynamic economic dispatch，DED）是电力系统调度中一类复杂的单目标优化问题，该问题的目标是确定调度周期内各机组的最优输出功率［1，2］，以满足负载需求及线路功率传输损失。由于DED考虑了发电机组的爬坡率约束，使得其非常适合实际电力调度场景，这对电力公司的机组调度具有较大的指导价值。然而，DED未考虑发电机组在燃煤过程中的污染排放，这与企业和政府越来越关注的人类健康环境问题背道而驰。因此，近年来许多研究工作将污染排放纳入动态经济调度模型的构建，从而衍生出一种更为复杂的动态经济环境调度（dynamic economic emission dispatch，DEED）模型。该模型同时优化发电成本和污染排放，并考虑机组爬坡率、负荷需求等约束［3，4］，使得该问题属一类含大规模约束的高维多目标优化问题。鉴于该问题的复杂性和实用性，开发高效的求解算法以获得满意的调度方案显得尤为重要，这对实际工程问题的求解和实现我国“双碳”目标具有重要的理论和现实意义。

求解多目标DEED模型的传统优化方法是通过权重法将其转换为单目标问题，采用拉格朗日乘子［5］、梯度［6］、二次规划［7］和动态规划［8］等数学规划方法获取最优调度方案。这些方法充分利用梯度信息搜索起始点附近的最优解。然而，由于机组频繁启停产生损耗剧增的阀点效应，考虑阀点效应成本的DEED模型具有多个局部最优解且目标函数非凸和非光滑，而数学优化方法对选取的起始点极为敏感，往往难以有效处理这类含多个局部最优解的复杂问题优化。所以，许多智能优化方法被开发来解决DEED问题，如进化算法（evolutionary algorithm，EA）［9］、粒子群优化（particle swarm optimization，PSO）［10，11］、差分进化（differential evolutionary，DE）［12，13］、和谐搜索算法［14］、教学优化［15］、生物地理优化［16］等。在文献［9］中，基于非支配排序遗传算法Ⅱ（NSGA-Ⅱ），提出一种二次多项式求根法获得满足功率平衡约束的机组功率分配策略。然而，该方法获得的第N个发电机的功率水平仍可能超出机组的功率上下界。文献［12］針对DEED问题开发了一种多目标差分进化（multi-objective differential evolutionary，MODE）算法，采用上述约束处理机制，以10机系统测试表明，MODE所获的Pareto前沿（pareto frontier，PF）优于NSGA-Ⅱ。文献［17］提出了一种模糊自适应修正θ粒子群优化算法。文献［18］设计了一种改进的θ多目标教学优化算法，利用模糊聚类技术对知识库的规模进行处理，从决策者的角度获得可行的调度方案。文献［2］开发了一种非优势DE算法，采用比例动态调整变量法调节机组功率范围的差异以处理功率平衡约束。文献［19］提出一种基于精英克隆的局部搜索DE算法，为提高算法开采和探索能力，增设精英群的克隆和突变机制，有效增强算法的全局搜索能力。文献［20］提出了一种自适应多目标差分进化算法，通过设计自适应的current to best/1交叉算子，有效地提高了传统进化算法的探索与开采能力。

虽然智能优化方法能获得DEED问题的有效解，但仍存在一些亟待解决的问题，如所获Pareto解的收敛性、分布性和多样性难于协调统一等问题。正如文献［21］所述，混合策略可能是解决复杂的DEED问题的更有效方法。文献［22］提出一种基于克隆选择的PSO算法，以传统的PSO算法为基本框架，嵌入克隆选择算子，从而加速算法的收敛性。本文为克服传统EA难以处理多个局部最优解以及收敛性差等问题，提出一种混杂免疫多目标优化算法（hybrid immune multiobjective optimization algorithm，HIMOA）解决带有阀点效应的DEED问题。处理该问题的难点在于决策空间高维性和约束的大规模性，致使已有算法直接求解易于陷入局部搜索或无法获取可行的非支配解，故解决该问题的策略是提高算法的搜索和开采能力，以获取更多的可行解，而克隆选择机制具有局部搜索和开采能力，能利用克隆机制产生大量的有潜力的解，并通过高斯变量扰动后，提高开采复杂区域的能力，同时采用修复机制对不可行的个体进行修复，从而提升种群中个体的可行性。故在HIMOA中，为了提升算法在高维决策空间的收敛速度，充分保存历代多样性的非支配解，选取存档中优秀个体进行克隆，采用改进的高斯突变策略对克隆体突变，实现收敛与开采的平衡。同时改进Deb［23］的可行性规则对存档中的个体进行更新，确保存档中非支配个体的多样性和分布均匀性。另外，为了应对功率平衡等式约束，提出一种逐步修复策略微调部分机组的出力，以提高群体中个体的可行性。数值实验以DEED问题的10机系统测试HIMOA的性能。结果表明，与同类算法相比，HIMOA获得PF的分布均匀性和延展性更具有优势，且近似于真实PF的程度更高。

本文的主要贡献是：a）构建了求解具有阀点效应的DEED问题的混杂多目标免疫优化算法框架；b）研究了HIMOA在处理大规模约束时的运行机制；c）设计了功率平衡方程的修复策略，以获得更多可行的解；d）以考虑阀点效应成本的10机系统为算例验证了HIMOA的求解能力，并与同类算法进行了比较，验证了本文算法的优越性。

1 DEED问题模型

电力系统DEED模型属一类含大规模约束的多目标优化问题，其目标是在满足大量的等式和不等式约束下，使发电成本和污染排放尽可能小。

然而，由HIMOA、MODE和NSGA-Ⅱ获得的最好折中值是不可比较的，但由HIMOA的污染排放2.9774×105相对于MODE的污染排放2.9642×105增加了1.32×103个单位，增加率为0.44%小于1，而HIMOA的成本2.5188×106相对于MODE的成本2.5463×106减少了2.75×104个单位，降低率为1.09%大于1。类似地，对于NSGA-Ⅱ，HIMOA的污染排放2.9774×105相对于NSGA-Ⅱ的污染排放2.9588×105增加了1.86×103个单位，增加率为0.63%，而HIMOA的成本2.5188×106相对于NSGA-Ⅱ的成本2.5414×106减少了2.26×104个单位，降低率为0.90%，HMIOA所获的折中解以增大少量的污染排放换取更低的发电成本。

为了可视化各算法25次独立执行所获的最好折中解在目标空间的分布情况，图2给出了基于模糊决策方法的各算法在25次运行中得到的最好折中解分布，其中approximative PF为近似的Pareto前沿（PF）。由图2（d）可以看出，HIMOA得到的25个最好折中解非常接近于近似的PF中心位置，这表明HIMOA每次执行能获得非常好的收敛性和分布性。然而，由图2（a）和（c）可以看出，MODE和NSGA-Ⅱ得到的最好折中解偏向于成本目标方向，特别是MODE的25个最好折中解远离近似的PF中心位置，且接近近似的PF程度时远时近，这表明MODE处理大规模约束DEED问题的稳定性和收敛性非常差。观察图2（b）发现，IMOEA/D-CH获得的25个最好折中解能位于近似的PF中部，然而其分布空间区域非常大且远离近似PF，这表明IMOEA/D-CH处理该问题时在某些次独立运行中能获得较好的收敛性，但一致收敛性差、稳定性弱。由上述比较分析表明，新提出的HIMOA在处理该问题时能表现出较稳定的搜索能力和较强的收敛性能。

为了观察各算法所获的PF效果，选取25次独立执行获得的PF中IGD指标值最小的一次PF进行比较。图3展示了各算法所获的PF分布。

由图3（d）可以明显看出，HIMOA得到的PF在目标空间中呈现出均匀的分布性，且分布范围非常广，所获的PF接近近似PF的程度非常高，这表明HIMOA所获的Pareto解多样性和收敛性非常好。由图3（a）和（c）可以看出，MODE和NSGA-Ⅱ所获的PF分布范围非常狭窄，这是由于该算法所获的最后Pareto解收敛于某一区域，陷入了局部最优，非支配解的多样性非常差，表明这两种算法难以处理这类复杂的优化问题，特别是MODE在接近近似PF方面表现非常差，这表明其对复杂的解空间开采能力弱，进化种群发生早熟现象。观察图3（b）发现，IMOEA/D-CH所获的PF分布性具有一定的均匀性，但PF的分布范围相对于HIMOA显得短窄，且在成本目标方向收敛性优于污染排放目标方向，这表明IMOEA/D-CH不能很好地平衡两个目标收敛性。由以上分析表明，HIMOA呈现较强的搜索和开采能力，能获得分布均匀且范围广和收敛性优越的PF，NSGA-Ⅱ和MODE的性能较差，仅能获得局部的PF，且收敛性弱。

为了从不同角度分析各算法25次独立执行所获性能指标HV、IGD、CR和SP的统计性能，图4给出这四种评价指标的箱型图。

图4（a）的HV箱型图显示，与MODE、IMOEA/D-CH和NSGA-Ⅱ相比，HIMOA实现超体积大的概率高，而MODE最差，这表明HIMOA所获的PF接近真实PF的概率高，而MODE所获的25次PF或远离真实PF，或PF的范围狭窄。对于CR指标，图4（b）显示HIMOA获得最好的CR统计特征，而NSGA-Ⅱ最差，这表明HMIOA所获的PF覆盖率大的概率高，而NSGA-Ⅱ所获得的25次PF或狭窄，或仅能得到部分非支配解。图4（c）箱型图表明，HIMOA获得IGD值较小的概率高，MODE获得大的IGD值概率高，这表明HIMOA所获得的PF均匀性和收敛性优于其他算法的概率大，其他算法中MODE获效果差的概率高。对于SP评价指标，图4（d）表明获SP最大的概率为IMOEA/D-CH，其次为HIMOA，这表明对于SP指标IMOEA/D-CH比HIMOA优越，这是由于IMOEA/D-CH所获的PF广度较HIMOA的概率高。

为了给出每台发电机组在HIMOA优化下的功率输出，选取HIMOA最好折中解时10台机组的各时段输出功率（表2），燃料成本为2.5188E+6（美元），污染排放为2.9774E+5（磅）。表2的最后列出了考虑传输损失的各时间段的传输损失（loss）。由表2可以看出，对于考虑传输损耗的10机系统的多目标DEED优化，各时段各机组的出力都得到了控制，各机组的爬坡率也得到了适当的满足。

4.4 策略分析及讨论

为了分析算法HIMOA中改进策略的优越性，本节以10机系统DEED问题作为测试实例，分析不同的约束阈值、不同的变异策略、不同的存档更新策略、有/无修复策略对算法收敛性能的影响。实验中HIMOA独立执行25次循环，每次循环的最大迭代数为2 000，计算每代所获PF與理论PF的IGD平均值，形成IGD随迭代数的变化曲线，分析改进的策略对算法收敛性和所获PF上点的分布性的影响。

图5给出了约束阈值ε取0、0.05、0.1、0.15和0.2五种情况时HIMOA对10机系统优化所获的IGD随迭代数的变化曲线。IGD是刻画算法所获PF收敛真实PF的程度，由图5的IGD变化曲线获知，ε取0时收敛性能最差，但ε在0.05～0.2较为相似，具体为：在ε取0.1时表现初始收敛速度快，随后陷入局部搜索；ε取0.15和0.2时初始收敛速度稍微慢，但最终与ε取0.05表现相当。图6分析了对克隆体采用三种不同的变异策略获得的IGD随迭代数的变化曲线。由图6可知，非均匀突变和多项式突变策略在初始阶段表现出快速的收敛，但非均匀突变到500代左右陷入了局部搜索，而多项式突变到600代左右收敛速度减慢，随后下降速度缓慢并一直保持平衡趋势。高斯突变初始下降速度具有一定的波动，并表现弱于其他两种变异策略，在1 000代左右所获的IGD值开始低于其他两种变异策略。这是由于本文采取的高斯突变表达式为uij=wij+1/g·N（0，1），其中第2项中1/g使得变异量随迭代数增大而变小，动态调整该系数使得算法具有精准的探索能力，N（0，1）为均值为0，方差为1的高斯变量。

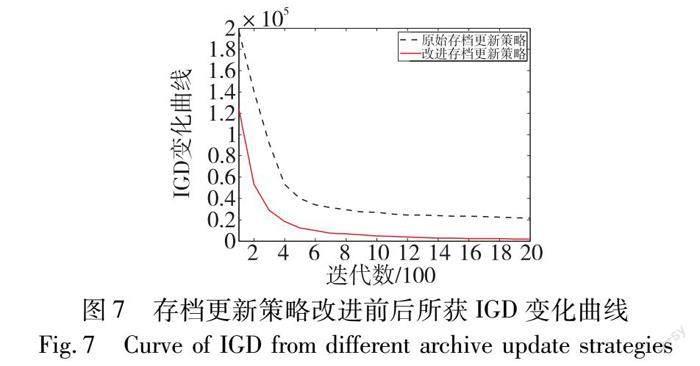
圖7给出了NSGA-Ⅱ中原始存档更新策略所获的IGD变化曲线与本文改进的存档更新策略下的IGD变化曲线。由变化曲线明显可知，改进的存档更新策略获得了更好的收敛速度，这表明改进的存档更新策略能有效提高算法对10机系统DEED问题的优化效果。这是由于改进的存档更新策略既能加大算法对可能空间的探索与开采能力，又能提升存档中非支配解的多样性，确保存档中非支配解的均匀分布。

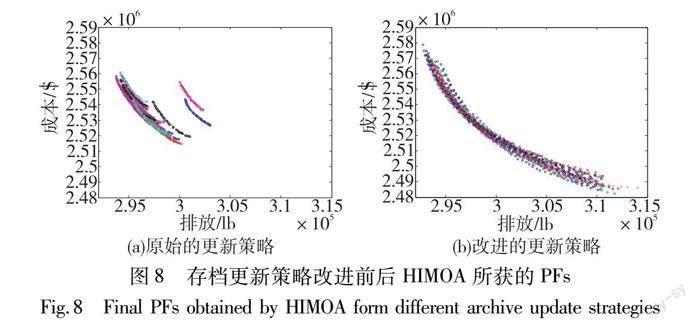
图8给出了25次独立执行所获PF分布。对比图8（a）和（b）明显可以看出，改进的更新策略25次所获PF均能保持很好的收敛性和分布性，而原始的更新策略仅能获得局部的PF，每次执行所获PF分布性和收敛性不统一。

图9分析了修复策略对算法HIMOA搜索性能的影响。其中图9（a）比较了有/无修复策略情况下进化种群中个体的非可行性比率随迭代数的变化曲线。由图9（a）可知，无修复策略时，种群中个体的非可行性比率随迭代数增加呈现下降趋势，但运行到2 000代时仍未达到0，这表明种群中还存在不可行的个体。而含修复策略情况下，在算法运行到1 000代左右时，个体的非可行性比率已达到0，这充分表明修复算子对提升个体的可行性比率有重大影响。图9（b）为有/无修复策略所获IGD随迭代数的变化曲线。由图9可知，含修复策略情况下算法所获的IGD变化曲线明显下降速度快，这表明算法的收敛性能好。

5 结束语

动态环境经济调度优化是计算机、管理学交叉学科中一类极具挑战性的研究课题，该问题具有多个局部最优点，且目标函数非光滑和非凸，传统的进化算法难以寻找全局最优解。本文提出了一种混合免疫多目标优化算法（HIMOA），并以10机系统的DEED问题进行测试。在算法设计中，采用修复方案处理功率平衡等式约束，提高了进化种群的可行性。为了增强传统EA的收敛能力，设计外部存档集保存非支配个体并提出新的裁剪策略更新外部存档，选择存档中优秀个体进行克隆，然后采用高斯策略对克隆体进行突变。将该算法作为一种搜索方法处理10机系统DEED问题，实验结果表明，相对于最新文献报道的方法，本文算法能够获得更好的性能，评价指标统计结果表明本文算法具有更好的统计性能。

与此同时，本文的工作还有待进一步的研究，以便应用于更复杂的DEED模型求解，如将所开发的框架引入模拟退火、蚁群、鱼群等其他搜索机制，应用于含其他能源的混杂DEED问题。另外，本文只在HIMOA中选取了一组固定的算法参数，而没有对本文算法进行参数调节或自适应设计，这将为开发自适应算法提供后期研究思路。

参考文献：

［1］Elattar E E. A hybrid genetic algorithm and bacterial foraging approach for dynamic economic dispatch problem ［J］. International Journal of Electrical Power & Energy Systems， 2015，69：18-26.

［2］Qiao Baihao， Liu Jing， Hao Xingxing. A multi-objective differential evolution algorithm and a constraint handling mechanism based on variables proportion for dynamic economic emission dispatch problems［J］. Applied Soft Computing， 2021，108： 107419.

［3］Jebaraj L， Venkatesan C， Soubache I， et al. Application of differential evolution algorithm in static and dynamic economic or emission dispatch problem： a review［J］. Renewable & Sustainable Energy Reviews， 2021，77： 1206-1220.

［4］Li Lingling， Liu Zhifeng， Tseng M L， et al. Improved tunicate swarm algorithm： solving the dynamic economic emission dispatch problems［J］. Applied Soft Computing， 2021，108： 107504.

［5］Yang Lingjian， Fraga E S， Papageorgiou L G. Mathematical programming formulations for nonsmooth and non-convex electricity dispatch problems［J］. Electric Power Systems Research， 2013，95： 302-308.

［6］Wood A J， Wollenberg B. Power generation operation and control［J］. Fuel & Energy Abstracts， 1996，37（3）： 90-93.

［7］Coelho L S， Mariani V C. Combining of chaotic differential evolution and quadratic programming for economic dispatch optimization with valve-point effect［J］. IEEE Trans on Power Systems， 2021，21（2）： 989-996.

［8］Ross D W， Kim S. Dynamic economic dispatch of generation［J］. IEEE Trans on Power Apparatus & Systems， 2007，99（6）： 2060-2068.

［9］Basu M. Dynamic economic emission dispatch using nondominated sorting genetic algorithm-Ⅱ［J］. International Journal of Electrical Power & Energy Systems， 2008，30（2）： 140-149.

［10］Zhang Yong ， Gong Dunwei， Geng Na， et al. Hybrid bare-bones PSO for dynamic economic dispatch with valve-point effects［J］. Applied Soft Computing Journal， 2014，18：248-260.

［11］Mason K， Duggan J， Howley E. Multi-objective dynamic economic emission dispatch using particle swarm optimisation variants［J］. Neurocomputing， 2017，270： 188-197.

［12］Basu M. Multi-objective differential evolution for dynamic economic emission dispatch［J］. International Journal of Emerging Electric Power Systems， 2014，15（2）： 141-150.

［13］Zhang Huifeng， Yue Dong， Xie Xiangpeng， et al. Multi-elite guide hybrid differential evolution with simulated annealing technique for dynamic economic emission dispatch［J］. Applied Soft Computing， 2015，34： 312-323.

［14］Fakhim-Babaei A， Nazari-Heris M， Mohammadi-Ivatloo B， et al. Economic dispatch of large-scale integrated heat and power systems by application of a novel harmony search approach［J］. Hybrid Energy System Models， 2021，52（3）： 25-49.

［15］Yang Zhile， Li Kang， Niu Qun， et al. A self-learning TLBO based dynamic economic/environmental dispatch considering multiple plu-gin electric vehicle loads［J］. Journal of Modern Power Systems & Clean Energy， 2014，2（4）： 298-307.

［16］Ma Haiping， Yang Zhile， You Pengcheng， et al. Multi-objective biogeography-based optimization for dynamic economic emission load dispatch considering plug-in electric vehicles charging［J］. Energy， 2017，135： 102-111.

［17］Bahmanifirouzi B， Farjah E， Niknam T. Multi-objective stochastic dynamic economic emission dispatch enhancement by fuzzy adaptive modified theta particle swarm optimization［J］. Journal of Renewable & Sustainable Energy， 2012，4（2）： 013102-6.

［18］Niknam T， Golestaneh F， Sadeghi M S. θ-multiobjective teaching learning-based optimization for dynamic economic emission dispatch［J］. IEEE Systems Journal， 2012，6（2）： 341-352.

［19］武慧虹， 錢淑渠， 刘衍民， 等. 精英克隆局部搜索的多目标动态环境经济调度差分进化算法［J］. 山东大学学报： 工学版， 2021，51（1）：11-23. （Wu Huihong， Qian Shuqu， Liu Yanmin， et al. Multiobjective dynamic economic emission dispatch differential evolution algorithm based on elites cloning local search［J］. Journal of Shandong University：Engineering Science， 2021，51（1）： 11-23.）

［20］武慧虹， 林妤， 曾茜， 等. 自適应差分进化算法及对动态环境经济调度问题应用［J］. 计算机应用研究， 2021，38（5）：1443-1448，1454. （Wu Huihong， Lin Yu， Zeng Xi， et al. Adaptive diffe-rent evolutionary algorithm and its application of dynamic emission economic dispatch problem［J］. Application Research of Compu-ters， 2021，38（5）： 1443-1448，1454.）

［21］Qian Shuqu， Wu Huihong， Xu Guofeng. An improved particle swarm optimization with clone selection principle for dynamic economic emission dispatch［J］. Soft Computing， 2020，24（20）： 15249-15271.

［22］Elaiw A M， Xia X， Shehata A M. Hybrid DE-SQP and hybrid PSO-SQP methods for solving dynamic economic emission dispatch problem with valve-point effects［J］. Electric Power Systems Research， 2013，103： 192-200.

［23］Deb K. An efficient constraint handling method for genetic algorithms［J］. Computer Methods in Applied Mechanics & Engineering， 2000，186（24）： 311-338.

［24］De Castro L N， Von Zuben F J. Learning and optimization using the clonal selection principle［J］. IEEE Trans on Evolutionary Computation， 2002，6（3）： 239-251.

［25］Panigrahi B K， Yadav S R， Agrawal S， et al. A clonal algorithm to solve economic load dispatch［J］. Electric Power Systems Research， 2007，77（10）： 1381-1389.

［26］El-Sharkh M Y. Clonal selection algorithm for power generators maintenance scheduling［J］. International Journal of Electrical Power & Energy Systems， 2014，57（5）： 73-78.

［27］Aragon V S， Esquivel S C， Coello C C. An immune algorithm with power redistribution for solving economic dispatch problems［J］. Information Sciences， 2015，295： 609-632.

［28］Deb K， Pratap A， Agarwal S， et al. A fast and elitist multiobjective genetic algorithm： NSGA-Ⅱ［J］. IEEE Trans on Evolutionary Computation， 2002，6（2）： 182- 197.

［29］Zhu Yongsheng， Qiao Baihao， Dong Yan， et al. Multiobjective dynamic economic emission dispatch using evolutionary algorithm based on decomposition［J］. IEEE Trans on Electrical and Electronic Engineering， 2019，14（9）： 1323-1333.

［30］Kukkonen S， Deb K. Improved pruning of non-dominated solutions based on crowding distance for bi-objective optimization problems［C］//Proc of IEEE International Conference on Evolutionary Computation. Piscataway， NJ： IEEE Press， 2006： 1179-1186.

［31］Qian Shuqu， Ye Yongqiang， Jiang Bin， et al. Constrained multi-objective optimization algorithm based on immune system model［J］. IEEE Trans on Cybernetics， 2016，46（9）： 2056-2069.

［32］Mason K， Duggan J， Howley E. A multi-objective neural network trained with differential evolution for dynamic economic emission dispatch［J］. International Journal of Electrical Power & Energy Systems， 2018，100： 201-221.

［33］Basu M. Particle swarm optimization based goal-attainment method for dynamic economic emission dispatch［J］. Electric Power Components & Systems， 2006，34（9）： 1015-1025.

［34］Wang Weiwei， Dai Shijuan， Zhao Wanzhong， et al. Multi-objective optimization of hexahedral pyramid crash box using MOEA/D-DAE algorithm［J］. Applied Soft Computing， 2022，118： 108481.

［35］Zitzler E， Thiele L， Laumanns M， et al. Performance assessment of multiobjective optimizers： an analysis and review［J］. IEEE Trans on Evolutionary Computation， 2003，7（2）： 117-132.

［36］Basu M. Dynamic economic emission dispatch using evolutionary programming and fuzzy satisfying method［J］. International Journal of Emerging Electric Power Systems， 2007，8（4）： 14-19.

收稿日期：2023-02-02；修回日期：2023-03-27  基金项目：国家自然科学基金资助项目（62241301，61762001）；贵州省教育厅创新群体重大研究资助项目（黔教合KY字［2019］069）；贵州省教育厅青年科技人才成长资助项目（黔教合KY字［2020］131号）；安顺学院研究生创新专项资助项目（asxysrt（202223）号）

作者简介：唐湘黔（1994-），男，贵州遵义人，硕士研究生，主要研究方向为智能优化算法及应用；钱淑渠（1978-），男（通信作者），安徽枞阳人，教授，硕导，博士，主要研究方向为计算智能、系统建模与控制（shuquqian@163.com）；武慧虹（1980-），女，山西太原人，教授，硕士，主要研究方向为智能优化算法、群與图．