爆破振动对邻近铁路隧道衬砌结构的影响

郭云龙 时步炯 孟海利 孙崔源 薛里

1.中国铁道科学研究院集团有限公司 铁道建筑研究所， 北京 100081；2.中国铁路上海局集团有限公司 杭州铁路枢纽工程建设指挥部， 杭州 310000

新建铁路隧道采用钻爆法施工时，爆破产生的振动可能会影响既有铁路隧道的运营安全。为了控制爆破振动对既有铁路隧道衬砌结构的影响，确定衬砌结构最大安全爆破振动速度至关重要。

许多专家学者对爆破扰动下既有隧道动力响应规律进行了研究。贾虎［1］对爆破扰动下邻近硐室围岩松动圈扩展机理进行研究，推导出计入爆破动载作用时中远区围岩松动圈厚度计算公式。陈俊桦［2］对水电站导流洞爆破时相邻隧洞动态响应情况进行现场监测和数值模拟研究，得到相邻隧洞迎爆侧直墙最容易受拉破坏。蒋楠等［3］利用LS-DYNA 有限元软件对爆破扰动下隧道结构动力响应进行数值计算，发现衬砌测点和围岩测点爆破振动速度衰减规律存在差异。王宏祥［4］利用有限元软件对山体爆破下既有铁路隧道的振动响应过程进行数值模拟分析，得出爆破振动效应会对列车安全运营产生不利影响。贾磊等［5］利用有限元软件对并行隧道爆破过程进行模拟分析得出，开挖进尺越大既有隧道迎爆侧衬砌振动速度越大，并行隧道间距小于3倍开挖洞径时间距变化对衬砌振动速度影响较大，埋深对衬砌振动速度影响较小。郑明新等［6］通过有限元分析得出，既有与新建隧道间距小于3 倍开挖宽度时间距对既有高速铁路隧道衬砌爆破振动影响较大，围岩质量越差衬砌爆破振动速度越大。陈壮［7］利用等效三角形荷载模拟新建隧道下穿既有铁路隧道时爆破过程，得出中心交汇处、已开挖处和未开挖处三个断面分别爆破时，既有铁路隧道振动速度均未超过安全限值。林立宏等［8］对原隧道扩挖爆破时近邻既有隧道的动力响应过程进行数值模拟，得到爆破地震波能量损耗大是导致既有隧道背爆侧振动小的原因。刘闽龙等［9］建立岩体各向异性动态损伤本构模型，通过数值模拟和现场损伤测试，验证该本构模型可用于爆破损伤模拟。唐先习等［10］对隧道初期支护混凝土爆破损伤进行研究，通过爆破振动测试和混凝土试块超声波损伤测试，建立损伤值与爆破振速的关系，依据纵波波速变化率不超过0.19 的规范要求，得到不同龄期混凝土试块的安全振速阈值。既有研究成果为邻近既有铁路隧道爆破施工提供了指导，但是针对邻近既有铁路隧道衬砌结构最大爆破振动速度的研究较少。本文依托并行隧道爆破工程建立爆破三维模型，结合现场爆破振动监测数据，验证模型的正确性。通过逐级提高爆破荷载，计算得到既有海南西环铁路隧道衬砌结构的最大爆破振动速度。

1 工程概况

邻近既有海南西环铁路隧道的新增复线全长约103 km，其中新建隧道爆破段长385 m，与既有隧道平行。两隧道中线间距在21.1 ～ 28.6 m，见图1。

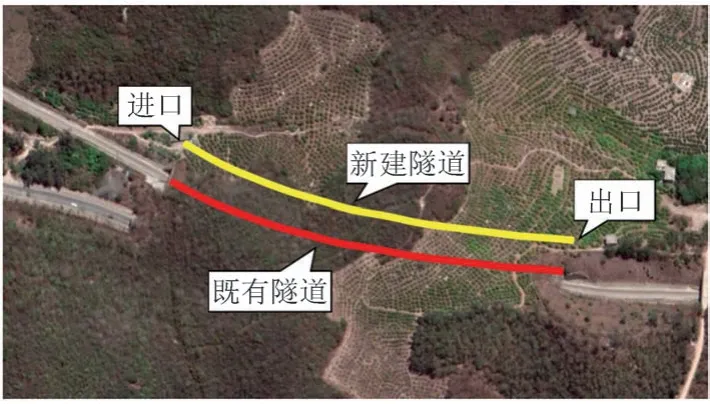
图1 新建隧道与既有隧道平面位置关系

隧址区未见基岩出露，受保家山断裂构造和不同时期花岗岩蚀变影响，岩体差异风化明显，节理裂隙发育，岩体破碎，围岩等级为Ⅴ级。新建隧道为单线铁路隧道，高10 m，宽8 m。采用三台阶法施工，隧道掌子面炮孔直径42 mm，炮孔深度2.5 ～ 4.0 m，装填岩石乳化炸药，光面爆破，数码电子雷管逐孔起爆。由于距离较近，新建隧道爆破产生的振动可能会对既有隧道衬砌结构的稳定造成影响。

2 爆破振动现场监测

为避免炮孔爆破产生的振动叠加效应影响分析结果，同时不妨碍正常施工，尽量选取炮孔起爆数量较少的工况进行爆破振动监测。新建隧道下台阶左侧采用5个炮孔爆破开挖。爆破设计参数见表1。

表1 下台阶左侧爆破设计参数

既有铁路属于运营线，列车通过频繁，故将爆破振动测点选在新建隧道已开挖区，距爆破掌子面42 m墙脚处，见图2。

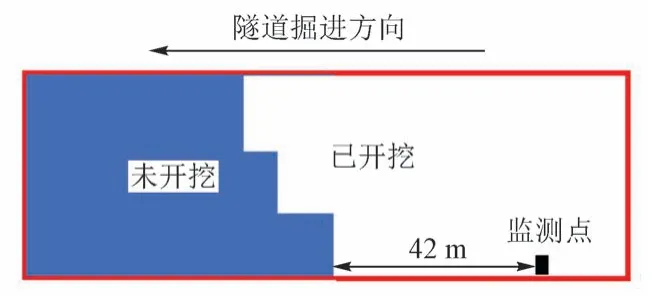
图2 测点布置

3 隧道爆破数值模拟

3.1 模型的建立

参照新建隧道设计尺寸、新建与既有隧道的位置关系，建立爆破三维模型，见图3。新建隧道与既有隧道平行，两隧中线间距21 m。模型尺寸为100 m（x轴） × 70 m（y轴） × 60 m（z轴），由六面体实体单元组成。既有隧道衬砌断面测点布置见图4。

图3 隧道爆破三维模型

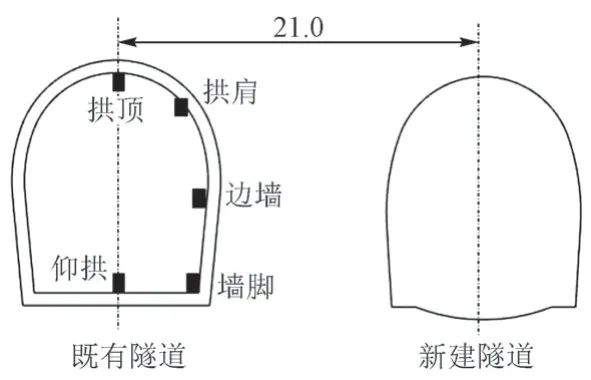
图4 断面测点布置（单位：m）

3.2 参数的确定

围岩采用摩尔库伦材料模型弹塑性单元模拟。既有隧道衬砌混凝土强度随时间推移有所降低，衬砌局部出现渗水、裂纹等现象。考虑最不利情况，衬砌采用C25 混凝土强度参数、弹性单元模拟。参考TB 10003—2016《铁路隧道设计规范》，确定Ⅴ级围岩和衬砌物理力学参数，见表2。

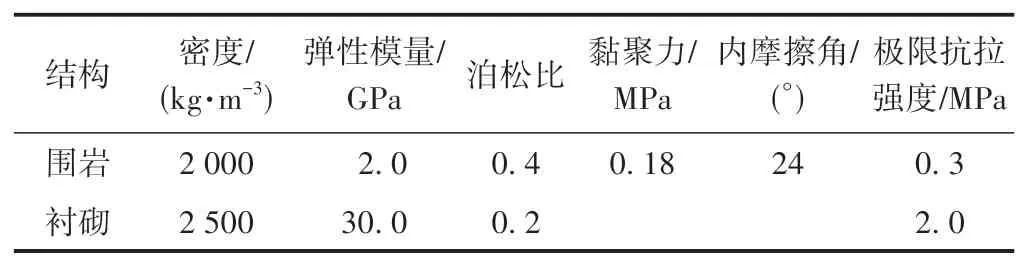
表2 围岩和衬砌物理力学参数

3.3 爆破荷载的选取

新建隧道爆破开挖时，在炮孔壁周围岩体激起爆破应力波，应力波强度骤增，达到峰值后又急剧下降，整个作用过程耗时极短，非常剧烈，故选择三角形等效爆破荷载模拟爆破过程。三角形等效爆破荷载的峰值Pmax通过半理论半经验公式［式（1）］计算得到。

式中：Z为比例距离，为炮孔中心到荷载作用面的距离，Q为单段装药量。

假定爆破荷载作用升压、降压时间分别为10、50 ms［11-13］，R= 1.0 m。由式（1）计算得到，单孔药量为1.2 、1.5 kg 时作用在开挖轮廓面上的Pmax分别为3.69、4.50 MPa。孔间延时为15 ms。将三角形等效爆破荷载施加在新建隧道下台阶左侧开挖轮廓面上，得到三角形等效爆破荷载时程曲线，见图5。

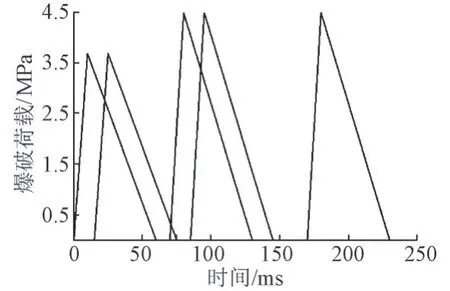
图5 三角形等效爆破荷载时程曲线

3.4 模型验证

在数值模型中选择与现场测点位置相对应的测点。测点爆破振动的实测和模拟波形见图6。可知：两者波形相似程度很高，实测爆破振动速度最大值0.34 cm/s，出现在100 ms；模拟爆破振动速度最大值0.37 cm/s，出现在81 ms。两者振动速度最大值相差8.8%，在可接受范围内。

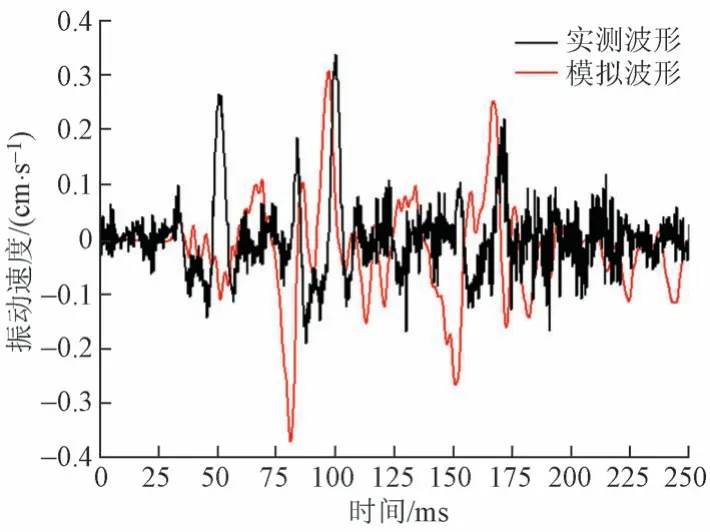
图6 测点爆破振动实测和模拟波形对比

对测点爆破振动曲线进行频谱分析，得到实测和模拟爆破振动波形的频谱曲线，见图7。

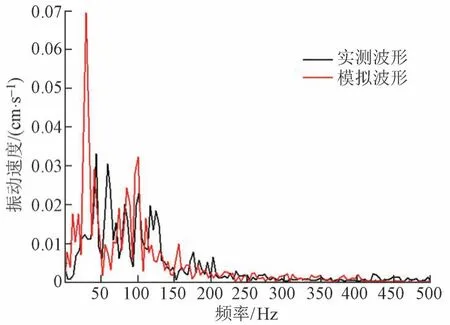
图7 实测和模拟波形的频谱曲线对比

由图7可知，实测、模拟爆破振动波形的频谱曲线主振频率分别为42.97、29.68 Hz，主振频率差值为13.29 Hz，在GB 6722—2014《爆破安全规程》中规定的主振频率差范围（10 ～ 40 Hz）内，满足爆破振动分析的要求。

综上，测点实测和模拟爆破振动的波形、振动速度最大值、主振频率接近，说明计算模型正确，可用于爆破振动分析。

3.5 计算结果分析

测点爆破振动速度最大值见表3。可知，新建隧道爆破时，邻近既有隧道衬砌结构各测点z向爆破振动速度最大。拱肩处爆破振动合速度最大，其值为1.84 cm/s；其次是边墙处，其值为1.78 cm/s。

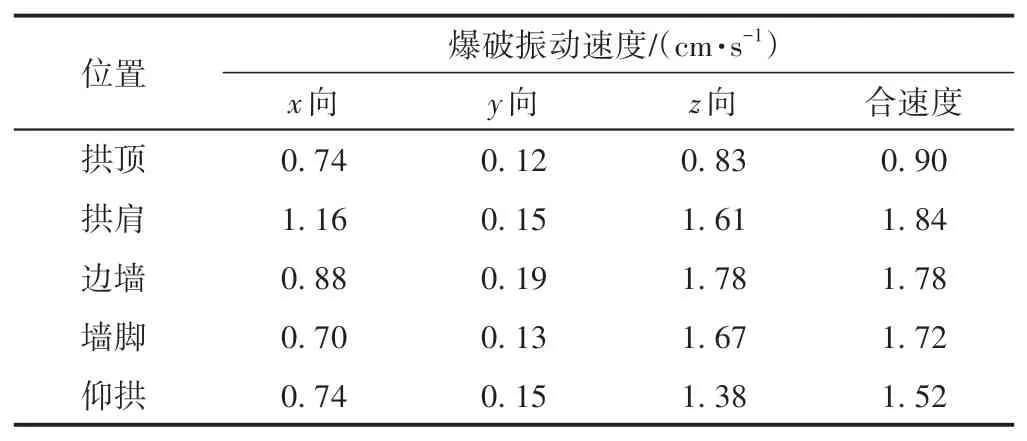
表3 测点爆破振动速度最大值

拱肩、边墙处z向爆破振动速度时程曲线见图8。拱肩、边墙处三个方向的爆破振动合速度时程曲线见图9。

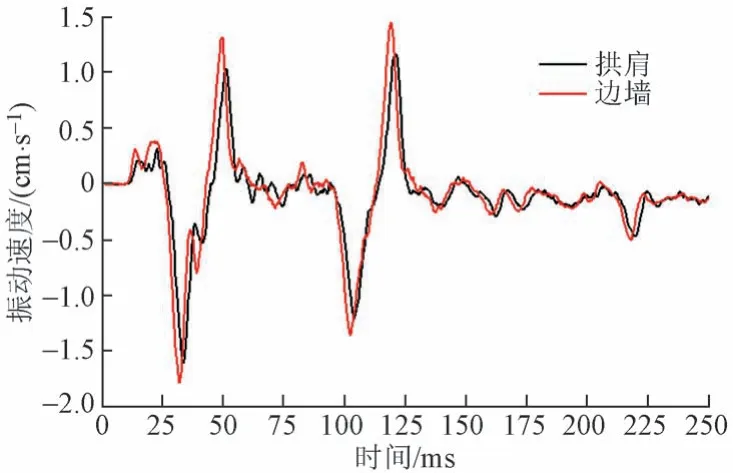
图8 拱肩、边墙处z向爆破振动速度时程曲线

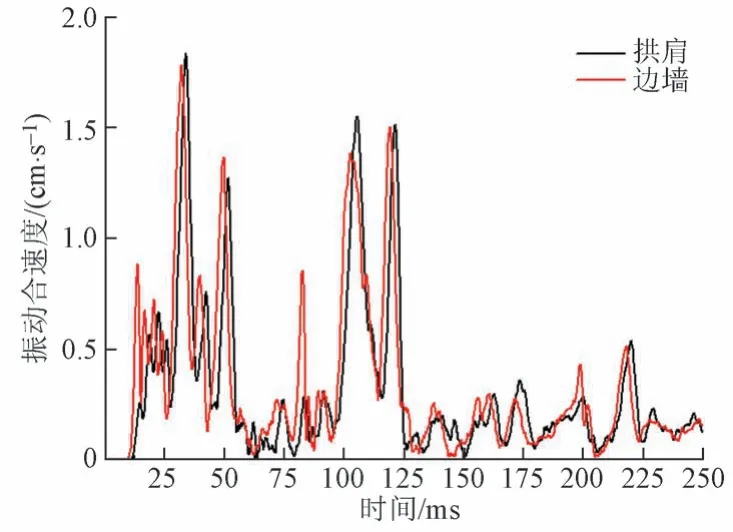
图9 拱肩、边墙处爆破振动合速度时程曲线

由图8 和图9 可知，新建隧道爆破产生的地震波引起既有隧道衬砌结构剧烈振动。爆破振动速度时程曲线分别在25 ～ 50 ms和100 ～ 125 ms出现明显的波峰波谷，在200 ～ 250 ms 出现的波峰波谷不明显。这是爆破地震波叠加效应所致。

既有隧道衬砌结构各测点最大应力见表4。其中：负值为压应力，正值为拉应力。可知：拱顶、拱肩、边墙和墙脚处均处于受压状态，只有仰拱处于受拉状态。

表4 既有隧道衬砌结构各测点最大应力MPa

仰拱处拉应力时程曲线见图10。可知：爆破扰动前，在0 ～ 12.5 ms 既有隧道衬砌结构仰拱处初始拉应力为141.7 kPa ；随着爆破地震波不断传入，在102 ms拉应力达到最大峰值149.3 kPa；爆破扰动结束后拉应力维持在146.0 kPa，与爆破扰动前相比仰拱处拉应力提高了4.3 kPa，说明爆破扰动对围岩的稳定性产生影响，导致围岩对衬砌结构仰拱处作用力增大。

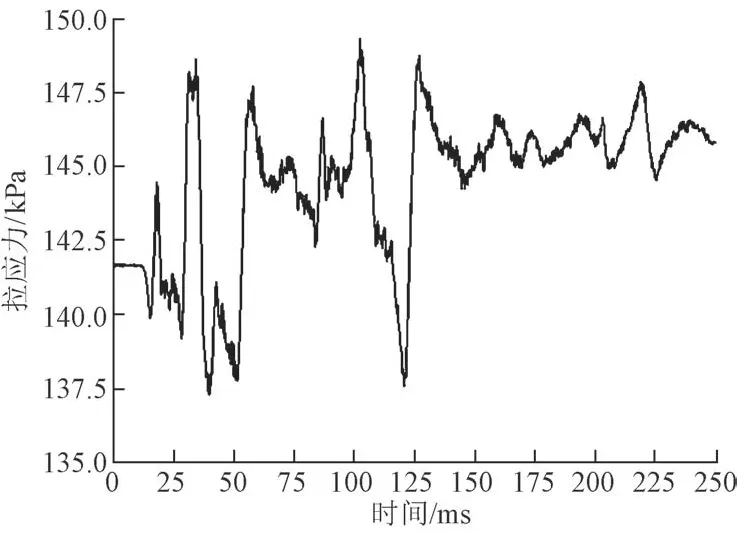
图10 仰拱处拉应力时程曲线

4 既有隧道衬砌结构最大爆破振动速度的确定

4.1 确定最大爆破振动速度的判据

以围岩塑性区是否贯通或衬砌混凝土所受拉应力是否超过其极限抗拉强度为判据，确定既有隧道衬砌结构的最大爆破振动速度。

新建隧道爆破时，爆破应力波在围岩中传播，并逐渐衰减为爆破地震波。当岩体所受爆破荷载强度大于其最大抗拉或抗剪强度时，将出现塑性区。新建隧道与既有隧道之间围岩塑性区贯通时，围岩发生塑性流动，从而失去承载能力，失稳破坏。

一般情况下混凝土容易受拉破坏，所受拉应力超过了其极限抗拉强度时将会产生裂纹。爆破地震波传播到既有隧道衬砌处，引起衬砌结构振动。当衬砌结构所受最大拉应力超过混凝土抗拉强度时，衬砌产生裂纹，发生破坏。此时对应的爆破振动速度即为隧道衬砌结构的最大爆破振动速度。

4.2 衬砌结构的最大爆破振动速度

保持其他参数不变，在3.3 节得到的三角形等效爆破荷载作用的基础上，逐级提高爆破荷载。分别对5、10、15、20、25倍五种爆破荷载工况进行计算。

4.2.1 围岩塑性区

对新建隧道爆破掌子面进行切片，得到不同工况下隧道围岩塑性区分布，见图11。其中：none 为弹性区；tension-n为当前拉伸破坏单元；shear-n为当前剪切破坏单元；tension-p为之前拉伸破坏单元；shear-p为之前剪切破坏单元。

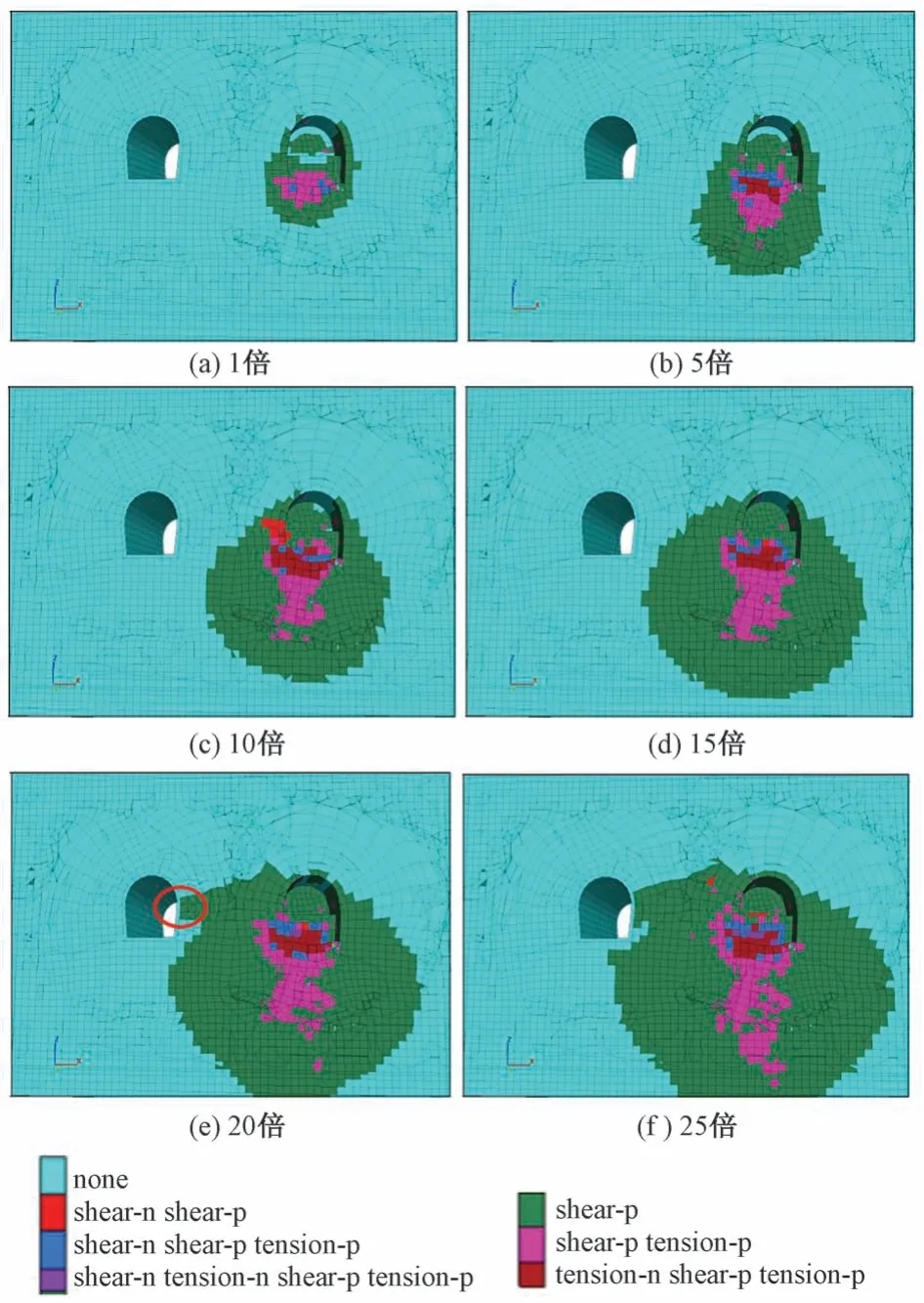
图11 隧道围岩塑性区分布

由图11 可知，随着爆破荷载不断提高，围岩塑性区范围不断增大。20 倍爆破荷载作用下新建隧道与既有隧道之间围岩塑性区贯通，围岩失稳破坏。此时既有隧道衬砌结构振动速度即为最大爆破振动速度。

4.2.2 衬砌结构最大爆破振动速度

各工况既有隧道衬砌结构不同部位最大爆破振动速度（三个方向的合速度）见表5。可知，随爆破荷载不断提高，既有隧道衬砌结构不同部位最大爆破振动速度均不断增大，其中边墙处最大爆破振动速度增长最快，拱顶处最慢。除1倍爆破荷载工况，其他工况下均是边墙处最大爆破振动速度最大，拱顶处最小。

表5 衬砌结构不同部位最大爆破振动速度

4.2.3 衬砌结构应力

各工况既有隧道衬砌结构不同部位最大应力见表6。其中：受拉为正，受压为负。

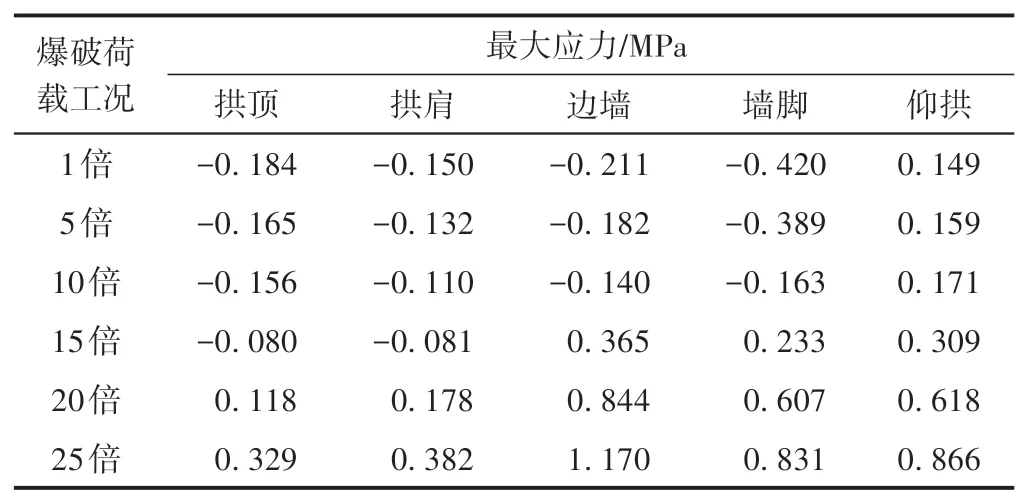
表6 既有隧道衬砌不同部位最大应力

由表6可知：随爆破荷载不断提高，既有隧道衬砌结构不同部位最大压应力均不断减小，最大拉应力均不断增大。爆破过程中衬砌拱顶、拱肩、边墙和墙脚处分别逐渐由受压转变为受拉，仰拱处始终受拉。边墙处最大应力增长最快，在25倍爆破荷载作用下边墙处最大拉应力达到1.170 MPa。这说明在相同爆破荷载作用下，既有隧道衬砌结构迎爆侧边墙处拉应力最容易超过混凝土极限抗拉强度。因此，边墙处最大爆破振动速度即为最大爆破振动速度，需要重点关注该速度是否在安全范围内。

结合表5 和表6 可知，既有隧道衬砌结构最大爆破振动速度与所受最大拉应力正相关，拟合得到既有隧道衬砌结构迎爆侧边墙处最大爆破振动速度（v）与最大拉应力（σmax）关系式，即

式（2）的拟合相关系数为0.974 4。C25 混凝土的极限抗拉强度为2.0 MPa（即σmax），通过式（2）反算得出极限抗拉强度下最大爆破振动速度为45.58 cm/s。

综上，20 倍爆破荷载作用下既有隧道与新建隧道之间围岩塑性区贯通，既有隧道衬砌结构爆破振动速度达到最大值。衬砌结构迎爆侧边墙处最危险，最大拉应力为0.844 MPa，最大爆破振动速度为29.90 cm/s。还未达到45.58 cm/s，既有隧道已破坏，故既有隧道衬砌结构迎爆侧边墙最大爆破振动速度取29.90 cm/s。

5 结论

本文对既有海南西环铁路新建隧道爆破过程进行模拟计算，通过现场振动监测数据验证所建隧道模型可用于爆破振动分析。通过逐级提高爆破荷载，分析了5、10、15、20、25倍五种爆破荷载工况下隧道围岩塑性区分布、既有隧道衬砌结构爆破振动速度和拉应力的变化规律。主要结论如下：

1）新建隧道爆破开挖时，既有隧道衬砌结构迎爆侧拱肩处爆破振动合速度最大，仰拱始终处于受拉状态。

2）随着爆破荷载不断提高，新建隧道与既有隧道之间围岩塑性区范围不断扩大，20倍爆破荷载作用下两隧间围岩塑性区贯通。

3）既有隧道衬砌结构最大爆破振动速度和最大拉应力正相关。与其他部位相比，衬砌结构迎爆侧边墙处最大爆破振动速度和最大应力均增长最快。

4）根据隧道围岩塑性区是否贯通或衬砌混凝土所受拉应力是否超过其极限抗拉强度两个判据，综合分析得出20 倍爆破荷载作用下既有隧道衬砌结构最大振动速度出现在迎爆侧边墙处，其值为29.90 cm/s。