黏滞阻尼器对铁路自复位桥墩地震响应的影响

张恒 夏修身 张旭东 乔鑫 祝浩然

兰州交通大学 土木工程学院， 兰州 730070

自复位桥墩采取分离设计桥墩和基础的思想。强地震作用下利用提离摇摆进行隔震，震后利用自重实现复位。Housner［1］最早提出弱化结构与基础连接的思想，使结构在强震作用下产生摇摆现象，从而避免破坏。Palermo 等［2-3］将残余位移作为抗震的性能指标，对自复位结构进行非线性时程分析，发现在较小残余位移的情况下，自复位结构体系依然具有较高的承载力。何铭华等［4］基于性能的设计理念，设计了一种自复位桥梁墩柱节点新体系，此体系设计应用灵活，实用性更强，震后残余变形小。夏修身等［5-6］给出了桩基础铁路高墩摇摆隔震的Winkler 弹簧模型，并提出了两弹簧模型、考虑限位的三弹簧模型，以及提离弹簧刚度的取值办法。史军［7］设计制定了一组带牺牲部件的自复位桥墩模型进行拟静力试验，并与OpenSees 分析结果进行对比，结果表明，牺牲部件起到了一定的耗能作用，且有限元结果和试验结果吻合良好。李帆等［8］研究发现外置分阶段耗能阻尼器的自复位桥墩比内置耗能钢筋的水平承载力更高，提高了桥墩的抗震性能。申彦利等［9］研究发现在装配式自复位桥墩外部设置软钢阻尼器表现出了良好的自复位能力、承载力和耗能能力，但此结构在内部设置了耗能钢筋，弱化了阻尼器的作用，也没有分析阻尼器对桥墩地震反应的影响。

黏滞阻尼器是速度型阻尼器，流动速度越大，产生的阻尼力越大，耗散的地震能力越大，大地震时可以保持稳定的性能，但关于桥墩底部设置黏滞阻尼器的文献鲜有涉及。本文提出一种外设黏滞阻尼器的自复位桥墩，基于OpenSees 平台建立自复位桥墩模型，讨论阻尼器参数对自复位桥墩墩顶位移和墩底弯矩的影响，并与无阻尼器自复位桥墩进行对比分析。

1 工程概况及有限元模型

1.1 工程概况

跨度32 m单线铁路简支箱梁桥［图1（a）］，桥梁下部结构为空心圆端形桥墩，群桩基础，承台尺寸12.7 m ×14.5 m × 3.0 m。为研究黏滞阻尼器对桥墩的影响，对18#墩进行再设计，使之成为自复位桥墩，详细的设计过程及参数见文献［10］。将黏滞阻尼器对称布置在墩底两侧［图1（b）］，每侧竖向布置5个，桥墩与原桥墩其余参数保持一致。

1.2 有限元模型

外设黏滞阻尼器的自复位桥墩有限元模型如图2所示。墩柱、桥跨质量和桥墩的提离采用文献［11］中的模拟方法。采用element elastic beam 模拟墩柱，刚臂单元模拟墩底扩大基础。刚臂刚度为单元最大刚度的100 倍。采用只受压弹簧模拟桥墩的提离，提离弹簧采用element zero length 模拟，材料本构关系采用弹性只受压材料uniaxial materialENT。根据文献［12］，墩底提离弹簧刚度（k）取2.1 × 108kN/m。黏滞阻尼器采用Maxwell 模型进行模拟［13］，在Maxwell 模型中需要定义三个参数，分别为阻尼器阻尼系数（C）、速度指数（α）及线性刚度（K）。K取值较大［14］，通常取C的100 ～ 10 000 倍，本文K= 1.0 × 106kN/m。C与α的具体取值在下文进行讨论。黏滞阻尼器单元选用element two node link单元模拟。

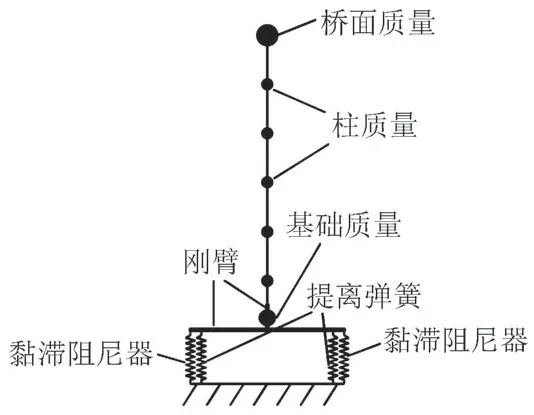
图2 外设黏滞阻尼器的自复位桥墩分析模型

从美国太平洋地震研究中心选取3 条近断层地震波，分别为1989 年Loma Prieta 地震波，1992 年Landers 地震波和1994 年Northridge 地震波，见表1。为了模拟8 度罕遇地震，将3 条地震波的幅值统一调整为0.57g。

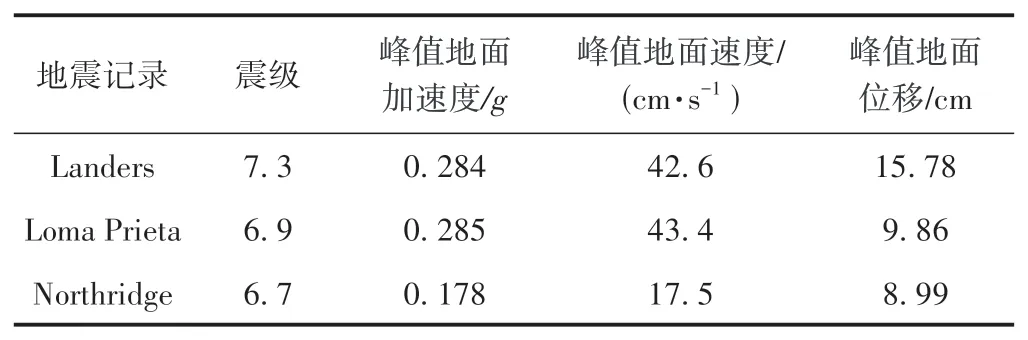
表1 地震动输入

2 阻尼器参数对地震反应的影响

C和α的取值不同，阻尼器对桥墩的影响也不同。因此，黏滞阻尼器参数的合理选取对结构减震效果影响很大。从抗震角度来看，C的常用范围为1 000 ～5 000 kN（s/m）α，α的常用范围为0.2 ～ 1.0。为讨论阻尼器力学参数对结构地震反应的影响，对α= 0.2、0.4、0.6、0.8、1.0，C=1 000、2 000、3 000、4 000、5 000 kN（s/m）α，共计25 种阻尼器参数组合进行非线性时程分析。墩顶最大水平位移和墩底最大弯矩随阻尼器参数变化曲线分别见图3 和图4。可知：①在Landers 地震波作用下，当α一定时，墩顶位移随C的增大而降低；当α= 0.2，C＞ 4 000 kN（s/m）α时，墩顶位移会出现上升的趋势。当C一定时，墩顶位移随α的增大而增大，这是因为阻尼器的阻尼力随α的增大而减小。②当C＞ 2 000 kN（s/m）α，α≤ 0.6时，墩底弯矩随C的增大出现明显的上升趋势；当α＞ 0.6时，墩底最大弯矩随C的增大整体呈减小趋势。当C一定时，墩底最大弯矩随α的变化比较复杂。Loma Prieta 和Northridge地震波作用下也有相似的变化规律。

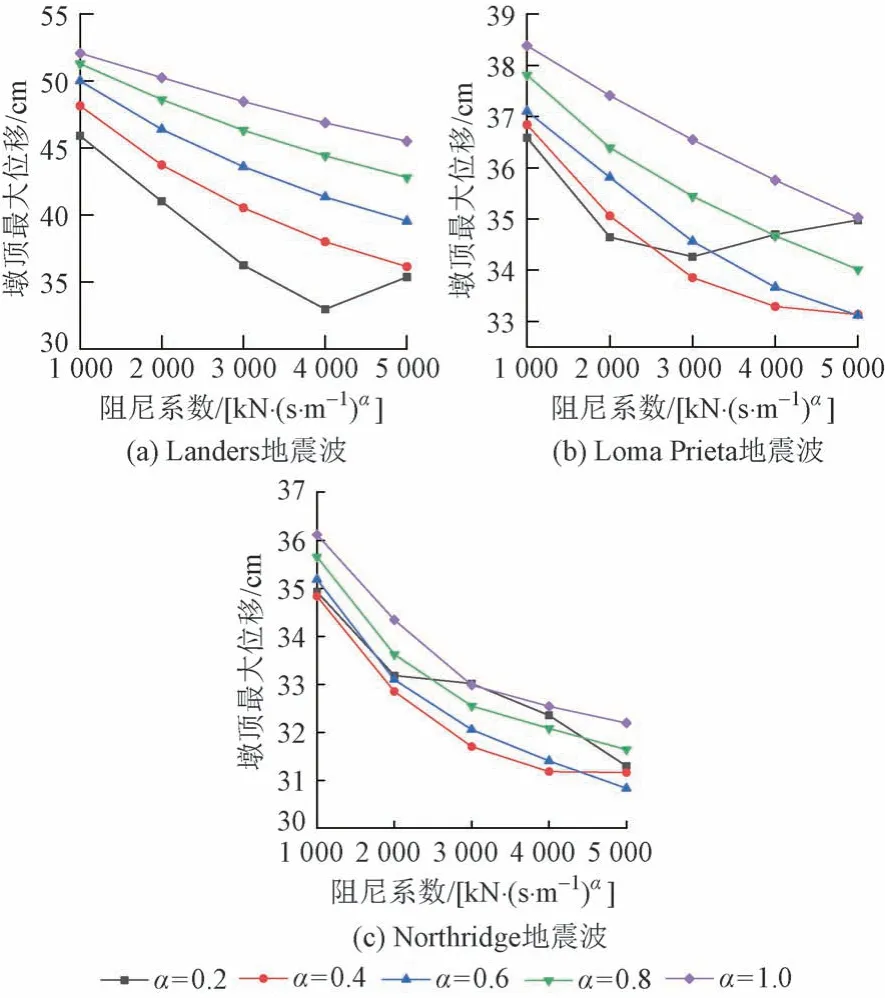
图3 墩顶最大水平位移随阻尼器参数变化曲线

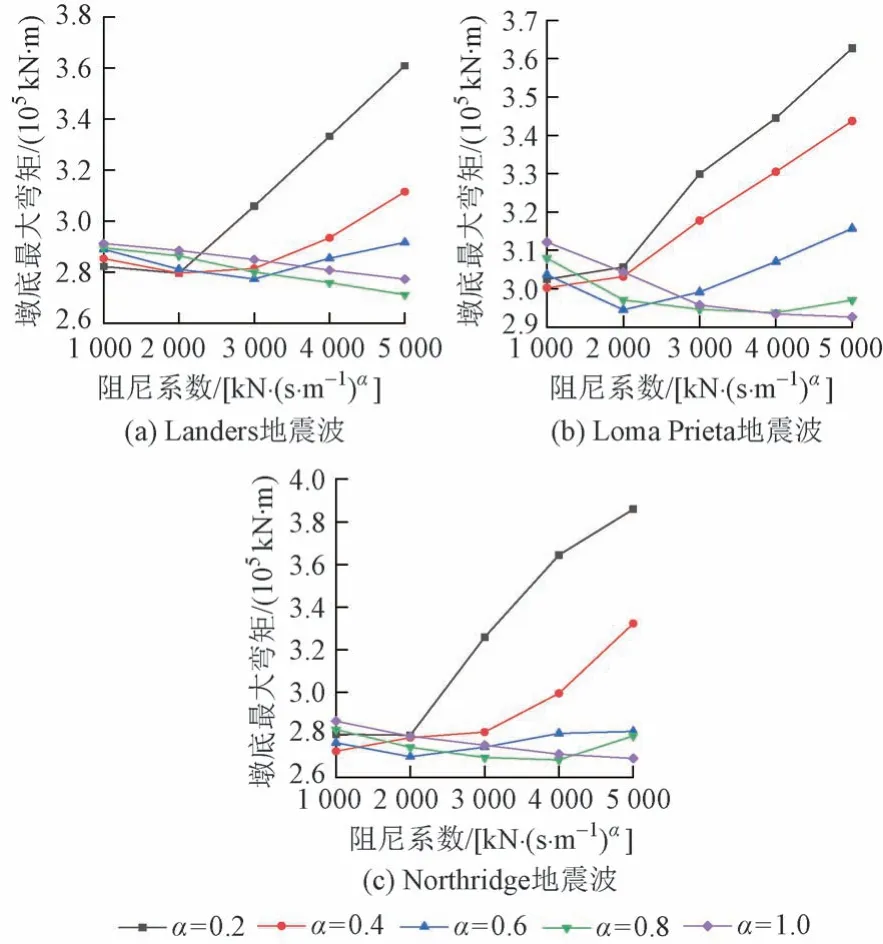
图4 墩底最大弯矩随阻尼器参数变化曲线

综上，不同阻尼系数与速度指数下墩顶最大位移与墩底最大弯矩的变化趋势不同，当α为0.2，C为2 000 kN（s/m）α时，墩顶位移与墩底弯矩综合减震效果较优。

3 有无阻尼器结果对比

为了深入研究墩底外设黏滞阻尼器自复位桥墩的地震反应，分析无阻尼器自复位桥墩（工况1）、有阻尼器自复位桥墩（工况2）的地震反应。α取0.2，C=2 000 kN（s/m）α，输入Landers波时桥墩时程曲线如图5所示。可知：①前10 s 内墩顶位移达到最大值，且工况2 小于工况1，这说明阻尼器起到了耗能作用，35 s后工况2的墩顶位移大于工况1，其他时间段二者基本吻合。②桥墩的竖向提离主要集中在10 ～ 15 s 和25 ～35 s，10 s 时出现最大提离位移；与无阻尼器自复位桥墩相比，阻尼器减小了最大提离位移和提离次数。③25 ～ 35 s时阻尼器减小了墩底弯矩；35 s 后工况2 墩底弯矩大于工况1，这可能是35 s 后阻尼器失去耗能作用导致墩底刚度增大所致；其他时间段内两种工况基本吻合。

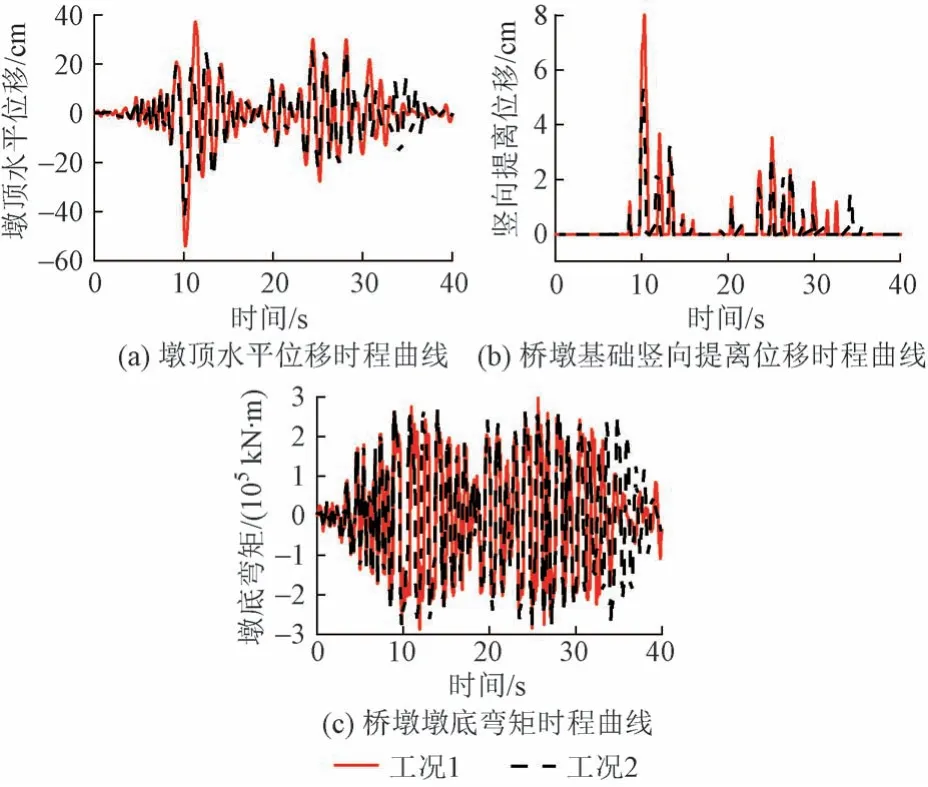
图5 桥墩时程曲线

两种计算模型下墩顶最大水平位移、竖向最大提离位移以及墩底最大弯矩见表2。可知：阻尼器能够减小自复位桥墩的墩顶最大位移、竖向最大提离位移以及墩底最大弯矩；在Landers 波作用下，墩顶最大位移和竖向最大提离位移减小效果最佳，降幅分别达到24.4%和33.8%；在Loma Prieta 波作用下，墩底最大弯矩减小效果最佳，降幅达到6.3%。

表2 两种计算模型下地震反应分析

黏滞阻尼器滞回曲线见图6。可知：黏滞阻尼器的滞回曲线近似呈半椭圆形，这是因为阻尼器布置在墩底无法出现负向位移；滞回曲线面积较为饱满，说明黏滞阻尼器发挥了主要的减震作用，且耗能能力明显。

4 结论

1）当速度指数（α）一定时，墩顶最大位移随阻尼系数（C）的增大整体呈降低趋势；当C一定时，墩顶最大位移随α的增大而增大。

2）当α≤ 0.6 时，墩底最大弯矩随C的增大总体呈增加趋势；当α＞ 0.6 时，墩底最大弯矩随C的增大出现降低趋势。当C一定时，墩底最大弯矩随α变化较为复杂。

3）对铁路自复位桥墩而言，α为0.2，C为2 000 kN（s/m）α最优。在近断层地震波作用下，与无阻尼自复位桥墩相比，本文阻尼器能够有效减小自复位桥墩的墩顶最大位移、墩底最大弯矩以及最大竖向提离位移。