非线性色散耗散波动方程混合元方法的超逼近分析

史艳华

(许昌学院 数理学院,河南 许昌 461000)

考虑如下非线性色散耗散波动方程:

(1)

其中,X=(x,y),∂Ω是矩形区域Ω的边界,u0(X),u1(X)是已知光滑的函数,f(u)关于u满足Lipschitz连续性,即

|f(u1)-f(u2)|≤L|u1-u2|,∀u1,u2∈R.

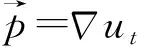
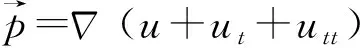
1 单元构造和混合元半离散逼近格式

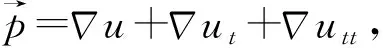
(2)

(3)

Vh={vh;vh|K∈P1,vh|∂Ω=0,∀K∈Γh},

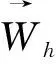
根据文[12-13],有下面结论.

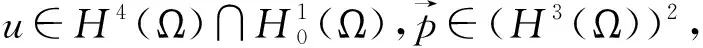
(4)

(5)

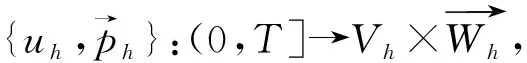
(6)

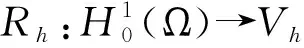
(7)

根据[14]知,投影算子Rh有如下逼近结果:

‖u-Rhu‖0+h‖u-Rhu‖1≤Ch3‖u‖3.

(8)

‖I1u-Rhu‖1≤Ch3‖u‖4.

(9)

2 半离散格式的超逼近分析

类似于文[6]中的分析,不难得到半离散格式(6)的解的稳定性结果.下面进行超逼近分析.

由方程(3)和(6),得误差方程

(10)

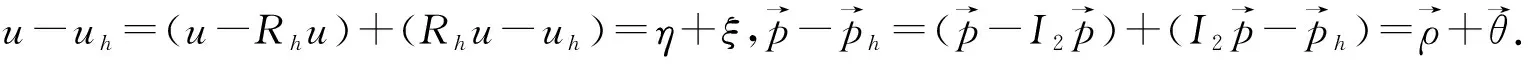
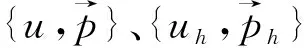
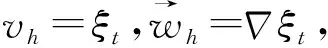
(11)

根据投影算子的性质(8),则

(12)

借助函数f(u)的Lipschitz连续性,得到

|(f(u)-f(uh),ξt)|≤L‖u-uh‖0‖ξt‖0≤L(‖η‖0+‖ξ‖0)‖ξt‖0

(13)

因此,

上式两边从0到t积分,并注意到ξ(0)=ξt(0)=0,再利用Gronwall不等式,有

再利用(9)得到

定理1的第一式得证.

(14)

根据(4)和(9)有

(15)

再借助(5)和定理1第一式的结果,(14)式可以估计为

(16)

类似于(12)(13)的估计可以得到

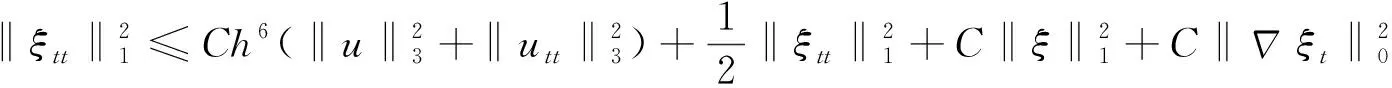
从而

(17)

将估计式(17)代入(16)中,得到

定理1的第二式得证.

3 全离散格式的超逼近分析

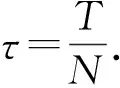
(18)

下面给出全离散格式下的超逼近结果.

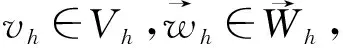
(19)

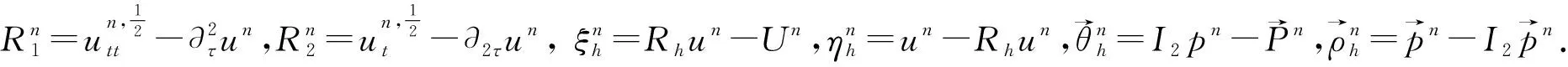
(20)

下面我们依次估计(20)式的右端项Ai,i=1,…,5.

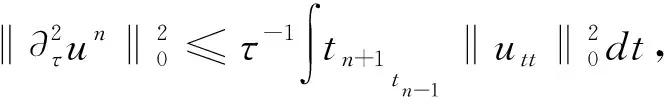
将以上估计式代入式(20),然后两边同时乘以4τ并且从1到n求和得

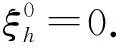
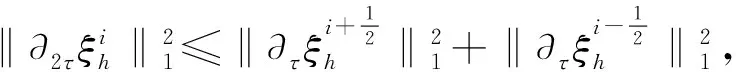
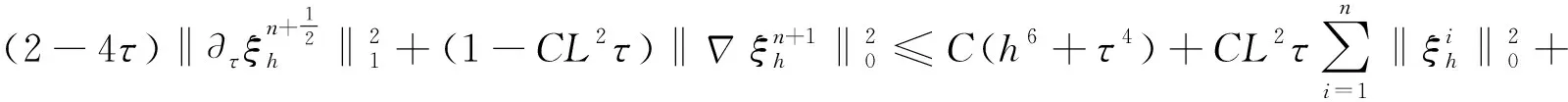
借助离散的Gronwall引理得

(21)

再利用插值算子I1与投影算子Rh之间的关系式(9)得到

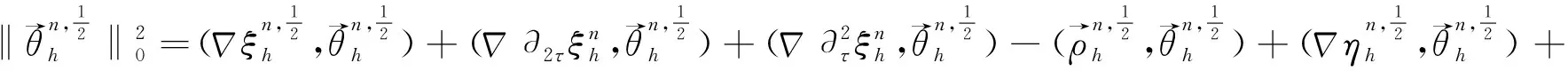
利用Schwartz不等式和结论(21),得

根据引理的式(5)得

类似于(15)式的估计可以得到

再由时间方向逼近格式的误差估计得

因此,

(22)

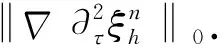
首先利用Cauchy不等式及定理2的第一个结论可以得到

类似于A1至A5的估计,得到

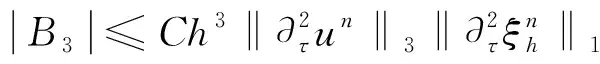
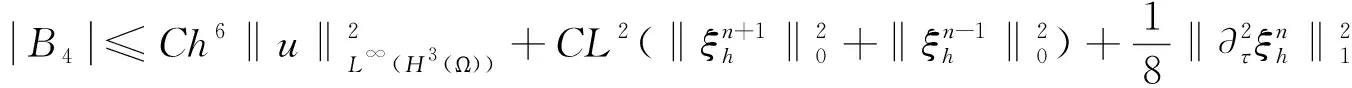
从而

将其代入式(22)得

结论得证.