基于终端滑模控制的四旋翼无人机编队控制*

王梓欣，成 炜，辛 颖，杨子安，黄子豪

(1. 北京动力机械研究所·北京·100074；2. 中国人民解放军93145部队·上海·201109；3. 上海航天控制技术研究所·上海·201109)

0 引 言

近年来，受到鱼群、鸟群、昆虫集群的启发，研究人员提出了多智能体系统(Multi-Agent Systems，MAS)[1]的概念，由每个独立个体组成群体，可以完成单个个体不能完成的任务。目前，多智能体系统已经渗透到自然和社会科学的众多领域，取得了较多成果，例如空间探索、安防巡演、军事侦察[2]等。在多智能体的研究中，无人机由于体积小、质量小、灵活性好，同时单架成本较低的优势受到重点研究[3]。无人机根据结构分为固定翼无人机和旋翼无人机，其中固定翼无人机飞行速度快，飞行时间长，负载更大，但是其控制难度和要求更高[4]，而旋翼无人机体积小、成本低、操作简单，并且可以实现垂直起降和悬停，成为多智能体系统领域研究的重点[5-6]。在旋翼无人机中，四旋翼无人机作为最常见的一种受到广泛研究。

在多智能体系统的研究中，编队控制受到学者的广泛研究和关注。编队控制要求预先设计一个可靠的队形，整个系统通过个体之间的通信在一定时间内形成并保持预先设计的队形，可以根据任务要求保持和调整队形。近十几年来，无人机编队控制理论和实物飞行领域取得了大量研究成果[7-11]，常用的编队控制方法主要包含领航跟随法、基于一致性方法、人工势场法、虚拟结构法和基于行为法。领航跟随法[12]是编队控制问题研究中最基本且最常用的方法，其将编队控制问题转化为误差跟踪问题，实现跟随者无人机对领航者无人机的跟随，但是编队控制的稳定性十分依赖于领航者无人机，跟随者之间没有通信和交互，整个系统的稳定性和鲁棒性较差，宾西法尼亚大学的Desai团队[13]针对该法做了大量的研究工作。同时，该法也是研究编队问题比较成熟的方法，在编队控制方面有着广泛的应用。基于一致性方法[14]的基础是一致性理论，相比于前者增加了个体无人机之间的通信和交互，根据自身信息和邻居信息进行动态调整，增加了系统的灵活性和鲁棒性，但是其控制算法更加复杂，对系统彼此通信的速度和准确性提出了更高的要求。人工势场法通过设计势场来实现编队队形，该法在解决避障问题中有很好的应用，但是其存在局部极小值的情况，同时缺乏稳定性证明[15]。虚拟结构法[16]常与领航跟随法相结合，弥补了领航跟随法过度依赖领航者的不足，提高系统的稳定性。文献[17]采用虚拟结构法研究无人机的编队控制问题，并用仿真实例验证了算法的有效性。基于行为法采用简单行为集合来形成控制器，其方法本身无法保证编队控制的精度，因而很难将其应用到无人机集群编队控制上。本文研究的四旋翼无人机系统采用“领航-跟随”结构，同时跟随者无人机之间存在通信，既能增强整个系统的鲁棒性和稳定性，又能根据领导者的位置信息进行编队分配，形成期望的编队队形。在控制方法的选择上，滑模控制可以设计滑动模态，需要调节的参数较少，同时可以克服系统的不确定性，对于干扰和建模误差具有很强的鲁棒性，其在工业控制、航空航天等领域具有广泛的应用，同时普通滑模控制在系统达到滑动模态时，无法在有限时间内误差收敛至0，终端滑模控制则可以使误差在有限时间内收敛到0，在编队控制上即可实现有限时间编队控制。基于此本文将以四旋翼无人机为研究对象，采用“领航-跟随”结构，同时保证网络中相邻个体的通信，根据每架四旋翼无人机本身和邻居信息设计终端滑模编队控制器，实现四旋翼无人机的编队控制，并且给出编队控制有限时间稳定性证明。

1 理论基础

1.1 四旋翼无人机数学模型

本文以四旋翼无人机为研究对象，考虑“领航-跟随”结构的同构四旋翼无人机的编队控制问题。其数学模型如下所示

(1)

假定每架四旋翼无人机期望偏航角ψdi已知，则通过上述加速度信号和期望偏航角可以得到如下公式

(2)

1.2 编队控制目标

本文研究具有“领航-跟随”结构的同构四旋翼无人机的编队控制问题，四旋翼无人机系统用有向图Gf=(V，E)表示，其中V={v1，…，vN}表示四旋翼无人机的集合，E=V×V表示两架四旋翼无人机之间的通信，定义通信拓扑图中第i架四旋翼无人机的邻居集合Ωi={vj∈V：(i，j)∈E}，其中vj表示第j架四旋翼无人机，|Ωi|表示第i架四旋翼无人机邻居的个数。

假设本文研究的四旋翼无人机系统的通信拓扑图Gf为连通图，共有N+1架四旋翼无人机，其中包含一个领导者(i=L)和N个跟随者(i=1，…，N)。定义通信拓扑图Gf的归一化拉式矩阵Υ，如下所示

(3)

式中，γij表示归一化拉式矩阵中第i行第j列的元素，其值如下所示

(4)

(5)

编队控制目标即所有跟随者四旋翼无人机的广义误差状态ei(t)收敛到0[18]。

2 四旋翼无人机编队控制

2.1 基于终端滑模的编队控制器设计

首先对第i架四旋翼无人机的广义误差状态ei(t)沿时间求二阶导数，得到如下公式

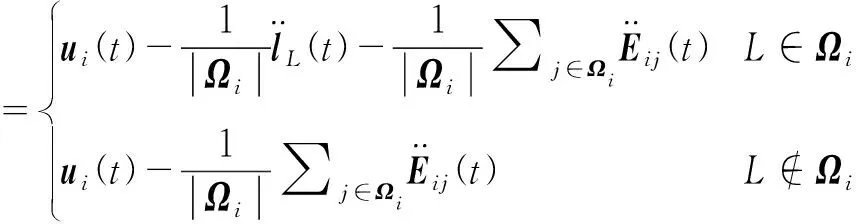
(6)

式中，

(7)

式中，ui(t)表示第i架四旋翼无人机编队控制器产生的控制信号。下面基于终端滑模控制方法设计四旋翼无人机系统编队飞行控制算法。

第i架四旋翼无人机的终端滑模函数定义如下

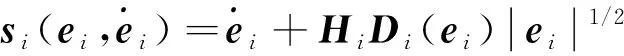
(8)

式中，Hi=diag{hi1，hi2，hi3}，him>0，m=1，2，3，Di(ei)=diag{sign(ei1)，sign(ei2)，sign(ei3)}，

第i架四旋翼无人机的终端滑模面如下所示

(9)

基于等速趋近律，得到第i架四旋翼无人机的终端滑模控制律如下所示

(10)

(11)

公式(10)即四旋翼无人机系统编队飞行控制律，当每架四旋翼无人机广义误差状态ei(t)收敛至0的时候实现期望的编队队形。

2.2 稳定性证明

下面基于李雅普诺夫稳定性理论结合有限时间稳定性理论给出上述编队控制器的有限时间稳定性证明。

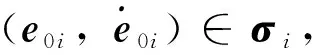
(12)

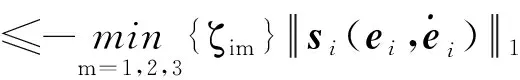
(13)

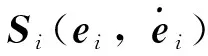
(14)

此时，考虑如下所示的Lyapunov函数

(15)

当ei=0时，Vi(ei)=0；当ei≠0时，Vi(ei)>0，因此公式(15)中的Lyapunov函数是正定的。对上述Lyapunov函数(15)求导

(16)

结合有限时间稳定性理论[18]可知，上述设计的编队控制器(公式(10))能保证第i架四旋翼无人机的广义误差状态ei在有限时间内收敛到0，实现四旋翼无人机系统的有限时间编队控制。

3 仿真实例及结果分析

3.1 通信拓扑图

本文研究的四旋翼无人机系统有向图中包含一个领导者(i=L)和三个跟随者(i=1，2，3)，通信拓扑图如图1所示，其对应的矩阵见公式(17)

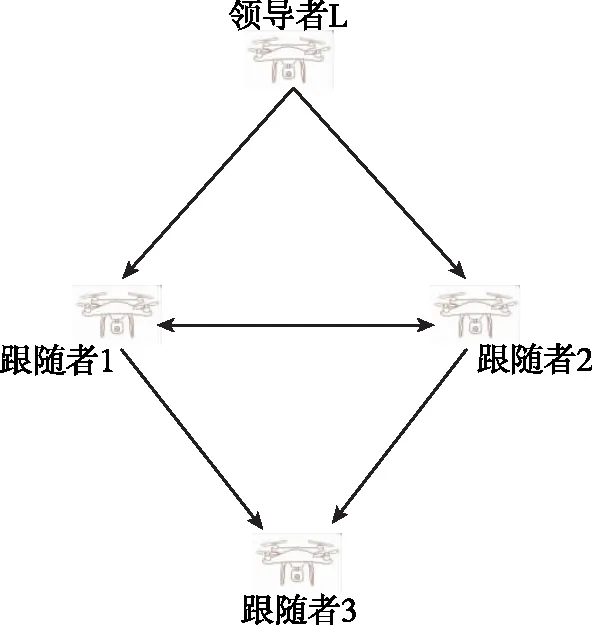
图1 四旋翼无人机系统的通信拓扑图Fig.1 Communication topology of quadrotor UAV system

(17)

3.2 初始状态和预期编队

首先给出四旋翼无人机系统跟随者的初始状态：

领导者四旋翼无人机的运动方程如下所示

四旋翼无人机系统的期望编队设置如下

3.3 编队控制器参数

1)终端滑模面参数Hi=diag(3，3，3)，i=1，2，3；

2)编队控制器增益矩阵Ki=diag(2，2，2)，i=1，2，3；

3)有界集合σi上界ψi=3.5，i=1，2，3。

3.4 仿真结果

对上述基于终端滑模的编队控制器效果进行仿真验证，同时与线性滑模控制器进行对比，验证所设计的编队控制器的效果。图2表示基于终端滑模编队控制器控制的四旋翼无人机系统三维运动图，图3表示基于终端滑模编队控制器控制的四旋翼无人机平面二维运动图，最终三架跟随者四旋翼无人机做螺旋上升的匀速圆周运动。

图2 基于终端滑模的三维运动图Fig.2 Three dimensional motion diagram based on terminal sliding mode control

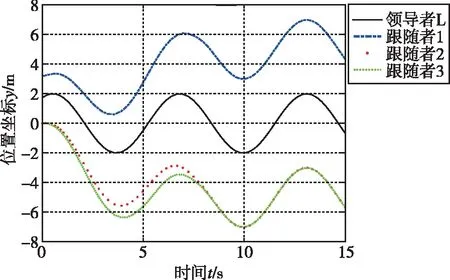
图4表示基于终端滑模编队控制器控制的四旋翼无人机系统位置坐标x，y，z随时间变化曲线，从图中可以看出，三架跟随者四旋翼无人机都可以跟随领导者四旋翼无人机在平面内做匀速圆周运动，高度上保持着编队队形设计的高度差。

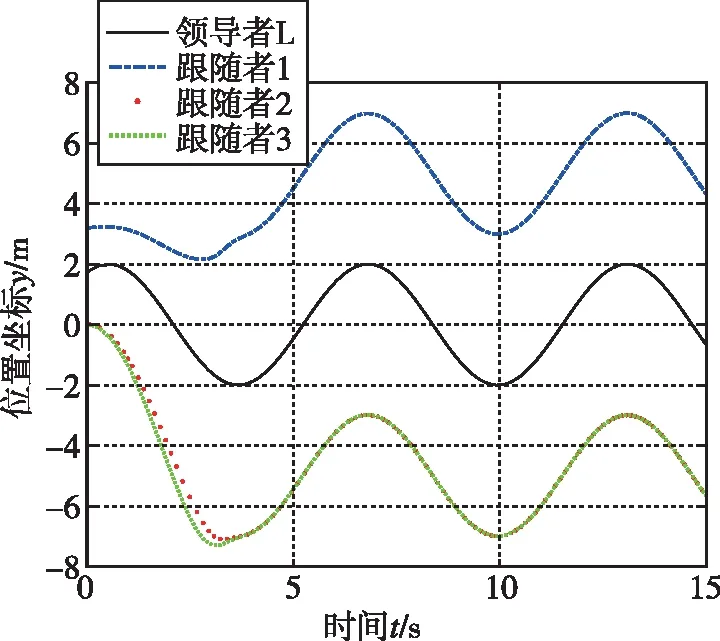
(b)位置坐标y

(c)位置坐标z图4 基于终端滑模的位置坐标变化曲线Fig.4 Position coordinate curve based on terminal sliding mode control

图5表示基于终端滑模编队控制器控制的四旋翼无人机系统广义误差状态收敛曲线，由图可以看出三个跟随者无人机广义误差状态在4s的时间内能收敛到0，实现了期望的编队队形。

图5 基于终端滑模的广义误差状态曲线Fig.5 Generalized error state curve based on terminal sliding mode control

为了验证所提出控制器的效果，设计了线性滑模控制器的对比实验，线性滑模函数设计如下

(18)

对应的线性滑模面如下

(19)

图6～图9表示四旋翼无人机系统在线性滑模控制器下的响应曲线。由曲线可知，基于线性滑模控制的四旋翼无人机系统的广义误差状态在9 s的时间内能收敛到0，也可以实现期望的编队队形，但与终端滑模控制相比，收敛的速度更慢，因而所设计的基于终端滑模的四旋翼编队控制具有更快的响应速度，控制效果更好。且由前文稳定性证明可知，结合有限时间稳定性理论，基于终端滑模控制的四旋翼编队系统可以实现四旋翼无人机的有限时间编队控制。

图6 基于线性滑模的三维运动图Fig.6 Three dimensional motion diagram based on linear sliding mode control

图7 基于线性滑模的平面二维运动图Fig.7 Two-dimensional motion diagram based on linear sliding mode control

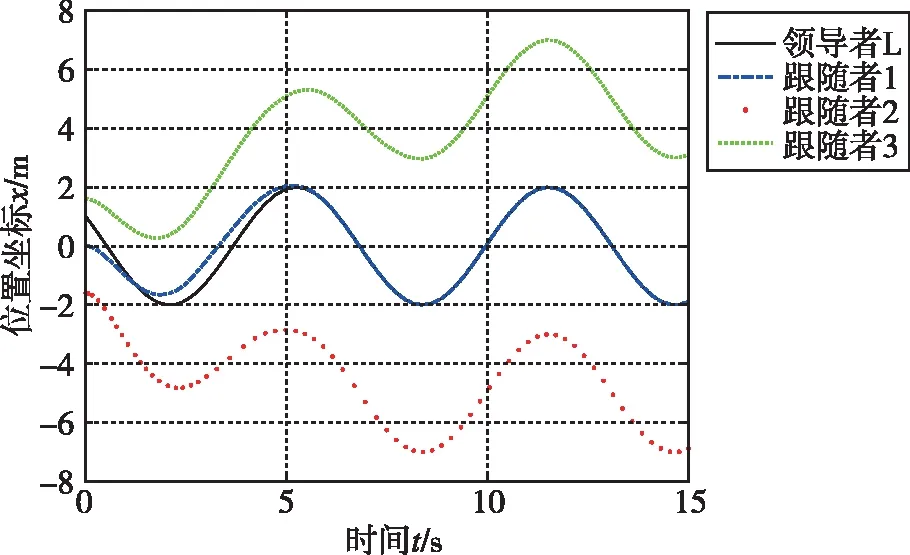
(a)位置坐标x

(b)位置坐标y

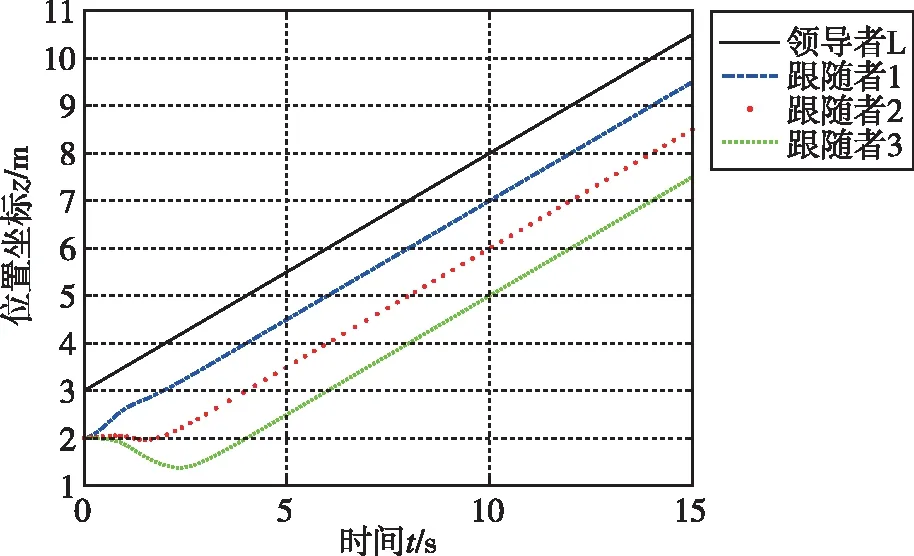
(c)位置坐标z图8 基于线性滑模的位置坐标变化曲线Fig.8 Position coordinate curve based on linear sliding mode control

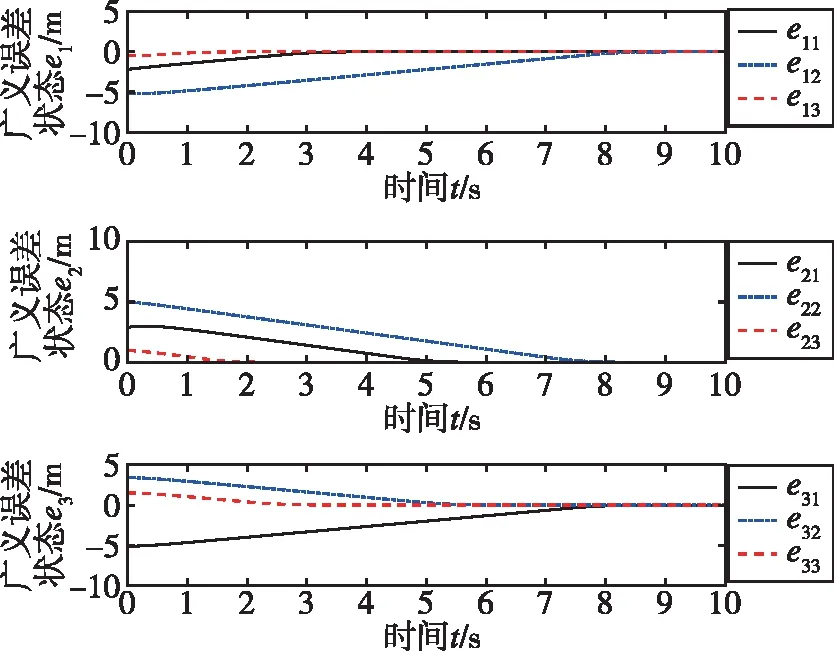
图9 基于线性滑模的广义误差状态曲线Fig.9 Generalized error state curve based on linear sliding mode control

4 结 论

研究了基于终端滑模控制的四旋翼无人机系统的编队飞行控制问题。以四旋翼无人机为研究对象，提出了编队控制目标，为每架四旋翼无人机设计了终端滑模编队控制器，并且实现了多四旋翼无人机系统的有限时间编队飞行。但是考虑到四旋翼无人机实际飞行时的干扰问题，并且滑模控制器本身存在一定的抖振问题，因此后续将针对文中未解决的问题进行进一步探索和研究。