基于改进灰色马尔可夫的港口货物 吞吐量预测研究

丁天明,潘 宁,杜柏松,艾万政

(浙江海洋大学 船舶与海运学院,浙江 舟山 316022)

0 引 言

港口货物吞吐量决定着港口资源分配的效率,直接影响着港口发展规划的合理性、科学性与先进性。对未来港口的长期发展规划和决策来说,预测是至关重要的一步[1],因此提高港口货物吞吐量的预测精确度就显得尤为重要。目前对吞吐量的预测方法有时间序列[2]、概率统计[3]、指数平滑[4]、灰色理论[5]、支持向量机[6]、神经网络[7]以及组合预测等。其中,组合预测方法应用较多:李长安等[8]将反向传播神经网络模型在蚁群算法的改进下进行吞吐量预测,加快了原始模型的收敛速度,提高了预测的精度,但是当数据不充分时,神经网络处于失效状态,因此该算法还有待提高;徐勇[9]通过灰色理论构建了原始预测模型,在分析吞吐量时间序列的趋势之后,实现了其精准预测的目的;TANG Shuang等[10]选取了5种影响因素,使用数据集建立多元线性模型和反向传播神经网络模型分别对上海港和连云港进行了预测评估;翁志坚等[11]针对灰色系统在预测有较大波动的数据序列过程中存在的缺陷,在马尔可夫理论基础上建立了新维灰色预测模型;王振振等[12]将各季度影响吞吐量的程度用加权灰色关联分析进行了排序,再结合三次指数平滑法与马尔科夫模型,大幅度提高了预测精度。

由于港口货物吞吐量的样本数据相对较少,信息量较匮乏[13],给预测过程带来了一定的难度,而灰色模型对样本数据没有过高的要求,可以以简便的方式运用小规模数据对非平稳随机过程进行预测并反映出序列的长期发展趋势,因此该模型目前在吞吐量预测方向的应用最为广泛[14-16]。但灰色模型在处理有波动性的数据时存在一定的缺陷,而马尔可夫过程能很好地解决这一问题,且其具有无后效性的特点,因此笔者用一阶马尔可夫链对模型残差进行修正,用以弥补灰色预测的误差精度。然而在目前的马尔可夫状态区间划分过程中均以中间值作为状态区间的白化系数,并没有随着实际区间的改变而调整。因此,笔者在马尔可夫修正的过程中还提出用粒子群算法对状态区间划分的参数因子进行动态优化,使其能自主适应区间数值的变化、及时更新马尔可夫链的每个状态区间系数并达到最优修正值。笔者将吸收以上3种模型算法的优点,通过粒子群算法迭代寻优,分别找到各区间最合适的白化系数,改进灰色马尔可夫预测模型,对比分析得到较高精度的吞吐量预测值。

1 基于货物吞吐量的模型建立

1.1 建立灰色预测模型

令非负原始时间序列为X(0)={x(0)(1),x(0)(2),…,x(0)(n)},经过一次加和生成后取得一阶加和总序列X(1)={x(1)(1),x(1)(2),…,x(1)(n)}。

建立灰色GM(1,1)一阶预测模型:

(1)

式中:参数a和b分别反应了模型的增长速度和协调变换关系。

此时模型对应的解用最小二乘法求解得到:

(2)

B和Yn表达式如式(3)、式(4):

(3)

(4)

令初始条件为x(1)(1)=x(0)(1),得出微分方程的解为:

(5)

(6)

再将模拟值进行累减计算,得到原始数据的预测值:

(7)

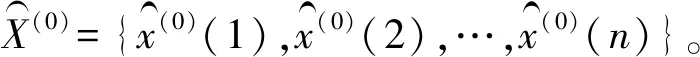
1.2 马尔可夫修正

马尔可夫链主要研究状态之间可能存在移动性的概率关系,事物的发展只与当前状态有关,与其他状态无关[17]。由于原始序列具有一定的波动性和随机性,使得GM(1,1)预测模型在实践过程中存在一定的误差。笔者用一阶马尔可夫对灰色预测模型进行残差修正,最大程度上克服了原始模型在数据波动上的局限性。马尔可夫链的特点是客观事物下一步的状态只与当前状态有关联,与除当前之外的所有状态均无关,即:

p′(Xt+1=j|Xt=i)=p′(Xt+1=j|Xt=it,Xt-1=it-1,…,X0=i0)

(8)

式中:Xn∈Ej,对任意的t∈E,i∈E,其中,E为等分区间集合,Ej为第j个等分区间。

由灰色系统理论得到的预测值可计算出与原始序列值的相对残差:

(9)

根据相对残差的大小来划分修正状态区间,每个区间的间隔相同,将其平均划分等分区间Ei=[Li,Ui],最后建立一阶状态转移矩阵Pij。该矩阵反映了各个残差状态区间移动过渡的可能性,即当前状态移动到下一个状态的概率:

(10)

Pij(m)=[Pij(1)]m

(9)

得出灰色马尔可夫预测模型如式(12):

(12)

其中,预测状态“高估”时取正,“低估”时取负。

1.3 粒子群优化白化系数

对于传统的灰色马尔可夫组合模型,状态区间取中值0.5未必为最优状态。笔者引进粒子群算法(particle swarm optimization, PSO)代替模型中直接取中值的方式,对马尔可夫模型各个状态i的参数因子进行优化。将白化系数λi带入灰区间求解:

Ii=λiLi+(1-λi)Ui

(13)

式中:λi∈[0,1];Li、Ui分别为状态区间的上、下边界值。

PSO算法是一种复杂适应优化算法,具有参变量少、全局搜索能力强、收敛速度快等优点[18]。其为一群随机的粒子在搜索空间上通过合适的速度不断地寻优迭代,找到最适合所有粒子的最佳位置,此时为最优解。而这些粒子均具有确定其好坏的功能,即适应度函数,在满足这个函数之后才能继续向前搜索。取m个粒子组合成一个群集,其中任一粒子q在d维空间中均有D维向量,每个向量均代表一个白化因子λq,每个粒子q均在空间里以速度vqd进行搜索,其搜索的位置xqd和速度vqd不断更新迭代,表达式为:

(14)

(15)

式中:学习因子c1和c2能够提高模型的收敛速度且避免陷于局部最优;r1和r2为[0,1]之间的随机数;w为惯性因子,可以使局部和全局搜索能力达到均衡;pbest,qd、gbest,qd分别为个体极值点、全局极值点的位置。

笔者用误差的均方差值eMS来衡量每个粒子优劣程度的适应度函数,此时均方差值越小越好。粒子适应度函数的表达式为:

(16)

基于PSO算法改进的灰色马尔可夫复合预测模型流程如图1。

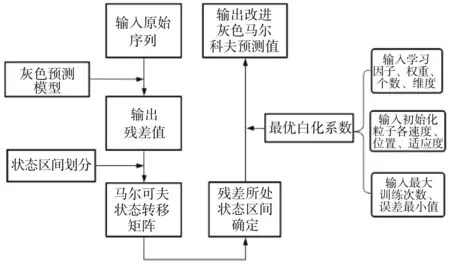
图1 基于粒子群优化的灰色马尔可夫货物吞吐量预测模型流程

算法步骤如下:

1)输入原始预测序列到灰色GM(1,1)模型中,得到残差值。

2)将残差值进行区间等概率划分并建立一阶状态转移矩阵。

3)根据状态转移概率矩阵确定各年份所处的状态区间。

4)输入粒子群算法的各项参数值并开始迭代运算,获取各区间的白化系数。

5)输出粒子群改进后的最终预测值。

1.4 精度分析

笔者通过对比分析各模型的方差比值和小残差概率值来判断各模型的预测精度。首先将预测数值与实际数值相减并取绝对值,得到绝对残差序列:

(17)

设原始序列X(0)的均方差为S1,残差序列Δ(0)的均方差为S2,方差比为二者比值:

(18)

小残差概率:

(19)

方差比值C越小表示当原始序列均方差S1相等的情况下,该模型的残差序列均方差S2越小,此时该预测模型残差饱和度小,精度高。小残差概率pr越大表示残差与残差平均值之差中小于原始定值0.674 5倍的数值越多,精度也越高,其精度判别见表1。

表1 后验差检验判别参照

2 实例应用

选用《中国统计年鉴》中2007—2021年宁波舟山港的港口货物吞吐量(表2)作为研究对象进行分析。分别将传统的灰色预测、灰色马尔可夫复合预测和粒子群优化的灰色马尔可夫这3种预测模型进行比较,找出最优精度的模型并预测未来3 a吞吐量情况,为后续港口生产建设提供理论依据。

表2 宁波舟山港2007—2021年货物吞吐量

2.1 GM(1,1)预测

由表2可以看出,宁波舟山港港口货物吞吐量总体呈平稳增长趋势。

将表2中数据进行累加得到一阶累加序列X(1)={47.336,100.284,157.968,221.268,290.661,365.062,446.040,533.386,622.315,714.524,815.457,923.896,1 035.905,1 153.145,1 275.55}。将此数据带入式(1),得到a=-0.060 4,b=53.062 2。进而一阶微分方程的解为:

(20)

从式(20)得出灰色预测的一阶累加序列模拟值,对其进行累减,即可得到原始序列对应的模拟预测序列和相对残差值,见表3。

2.2 灰色马尔可夫预测

根据表3中的残差序列,采用等概率方法对其进行状态划分,具体区间分为以下4个状态:极度高估E1、高估E2和E3、较为准确E4,其中每个状态区间误差间隔为3.5%,区间划分见表4。

表4 状态区间划分

根据各年残差值落入的状态区间划分各年份的状态。E1：2008,2009;E2：2010,2021;E3：2007,2011,2012,2015,2016,2019,2020;E4：2013,2014,2017,2018。

此时由式(11)建立一阶状态转移矩阵:

根据状态转移矩阵和各年份所处状态区间,将各年份的灰色预测值由式(12)进行修正,得出灰色马尔可夫复合模型的预测值,见表5。

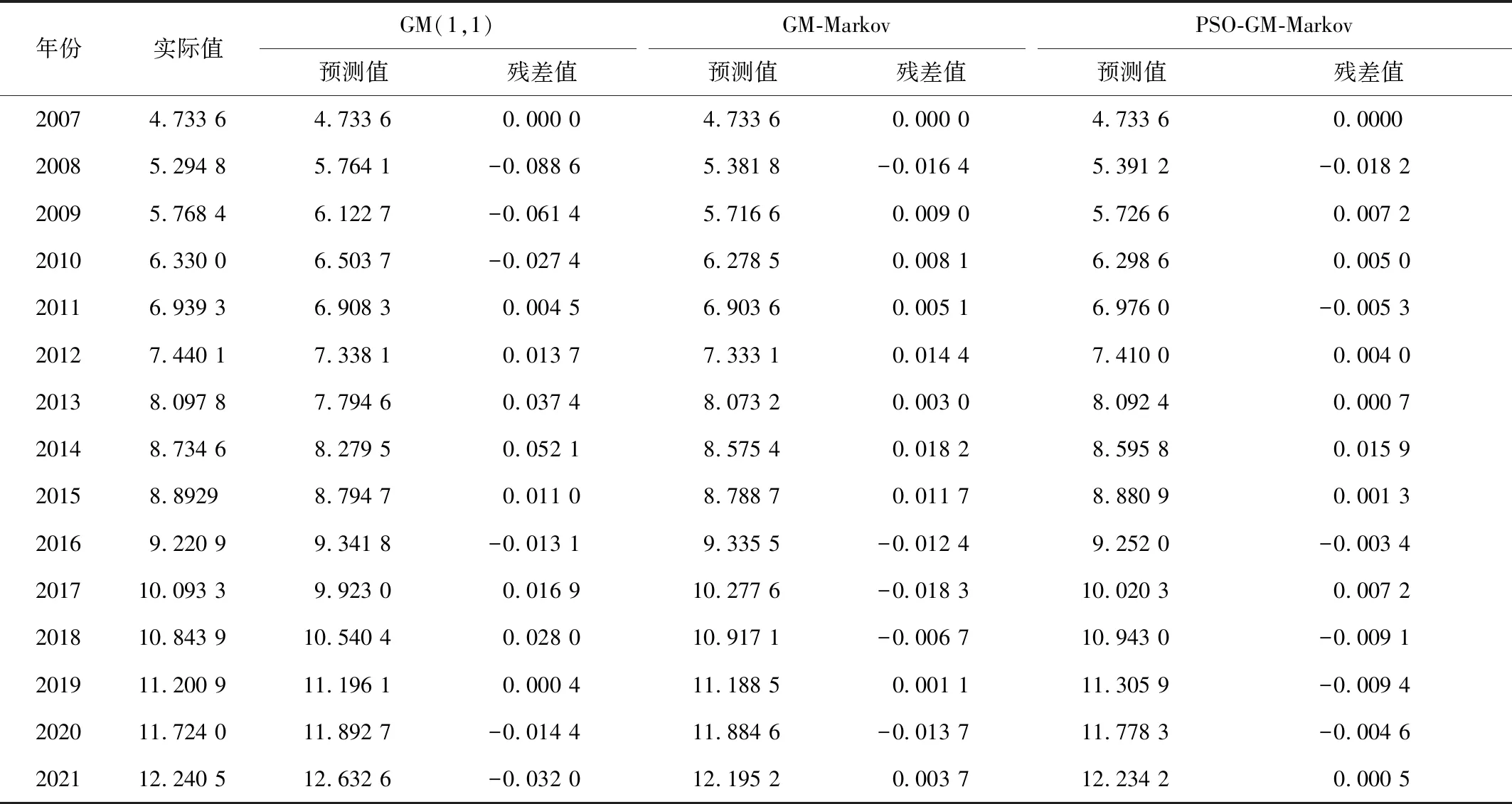
表5 宁波舟山港货物吞吐量3种模型预测对比

2.3 优化灰色马尔可夫预测

将2.2节中经过划分的4个残差状态区间视为灰区间,将这些灰区间的白化系数代入粒子群算法〔式(14)〕得到:

I1=λ1×(-0.088 6)+(1-λ1)×(-0.053 5)

(15)

I2=λ2×(-0.053 5)+(1-λ2)×(-0.018 3)

(16)

I3=λ3×(-0.018 3)+(1-λ3)×0.016 9

(17)

I4=λ4×0.016 9+(1-λ4)×0.052 1

(18)

而传统的灰色马尔可夫组合模型实际上是将其取中间值,即λi=0.5,i=1,2,3,4。事实上此4个区间状态并非均取中值。笔者利用粒子群算法迭代搜寻各状态区间实际参数,优化式(15)～式(18)的组合模型,确定当下合适的白化因子。

经过多次调试,取参数粒子长度为4,最大种群数为1 000,学习因子c1=0.6,c2=0.8,权重w=0.8,粒子最大更新位置为1,最小为0,更新速度最大、最小值分别为0.01、 -0.01。利用1.3节中粒子群算法的具体步骤,在MATLAB软件上运行程序得到优化后的动态白化系数λ={0.069 1,0.032 6,0.009 7,0.036 8}。由此可见,每个状态区间的系数取中间值0.5并不能达到最优预测效果。将优化后的λ值分别代入灰色马尔可夫组合预测模型,各状态区间进一步得到改进后的预测值见表5。

2.4 精度分析

对3种预测模型进行误差和后验差检验,如表6。由表6可知:3种模型的精度等级均为一级;相较于灰色GM(1,1)预测模型,灰色马尔可夫组合模型精度进一步提高,平均误差均值降低了62%;经粒子群改进灰色马尔可夫后的C值最小,精度也最优,平均误差均值下降了76%,相较于灰色马尔可夫组合模型下降了37%,这说明了经过二次修正后模型的拟合度更高。从图2中也可直观地看出,粒子群优化灰色马尔可夫模型的预测值与实际值更为贴合。因此,在马尔可夫修正模型中,参数直接取中间值的方法存在一定误差,而粒子群算法很好地克服了此模型的不足。

表6 模型精度对比

2.5 宁波舟山港未来三年货物吞吐量预测

首先对宁波舟山港的2022年货物吞吐量值进行预测,由式(11)可得到灰色马尔可夫组合模型的n步转移矩阵。同时选用与预测年份相隔最近4 a的转移步数和所在状态,建立状态转移矩阵,计算得到2022年的累积状态转移概率,如表7。从而确定2022年所处状态区间,最后根据状态区间划分(表4)和动态白化系数预测宁波舟山港未来货物吞吐量。

表7 2022年货物吞吐量状态预测

从表7可以看出,2022年累积状态转移概率最大为2.40,处于状态区间E3中,因此对应的区间参数为λ3。结合式(12)、式(13)可以得到2022年的吞吐量预测值,同理可得宁波舟山港2023年和2024年的货物吞吐量预测值,见表8。

表8 2022—2024年宁波舟山港货物吞吐量预测值

3 结 语

1)笔者选用易于实施的粒子群算法,对灰色马尔可夫模型在状态区间参数选择上的不足进行了改进。该算法影响参数较少,收敛速度快且具有良好的搜索能力,提高了模型的实用性。基于PSO算法改进后的灰色马尔可夫模型在残差均值上有一定幅度的下降,预测序列与原始序列基本拟合,很大程度上提高了复合模型的精确度,实现了对吞吐量的精准预测,为相关部门在港口规划和布局上提供了一定的参考价值。

2)笔者在用一阶马尔可夫链修正灰色残差值时,对状态的划分采用区间等分法,这直接影响到状态转移概率矩阵的确定,从而波及整个预测模型的精度。因此,可以对状态区间的划分做进一步改进,以期能够提高预测精度。