磁-球轴承复合支撑电主轴振动特性分析
徐方超, 王政鑫, 赵 川, 孙 凤, 金俊杰, 周峻宇, 赵海宁
(沈阳工业大学 机械工程学院,沈阳 110870)
随着高速切削加工行业的发展,机床在加工过程中,需要具有高转速的同时还需要保证较高的加工精度,已经成为一种必然的趋势。电主轴作为机床的核心部件,其性能直接影响机床加工系统的精度、稳定性以及应用范围。其中,限制主轴旋转的因素主要是动力驱动系统和轴承支承系统,而轴承作为主轴单元的重要组成部分,其支撑刚度的大小和支撑方式直接影响主轴的振动响应特性,进而影响主轴加工精度[1]。主轴转速越高,这种影响就越明显,改进主轴的支撑方式可以提高电主轴的振动特性。
国外对电主轴振动研究较早也比较成熟。Knospe[2]为了提高主轴高速切削过程中的稳定性、主轴动态刚度和增加承载能力,提出一种由3个径向磁轴承和1个轴向磁轴承支撑的电主轴,但这样也增加了有效控制的难度。Xu等[3]对电主轴转子中因不平衡质量产生的振动进行了仿真分析,得出振动幅值与不平衡的质量成正比。Raja等[4]分析了轴承发热对主轴振动性能的影响,并建立了电主轴热-结构耦合的模型,分析了热对主轴转子产生的变形以及对振动的影响。Qiao等[5]提出了电主轴柔性转子多节点不平衡振动的最优影响系数加权控制方法,仿真结果表明控制效果较好,但控制过程较为复杂。Wang等[6]为了抑制主轴由不平衡引起的振动,研发出带有平衡装置的自平衡电主轴,对其进行了模态和谐响应分析。
国内在电主轴加工过程中振动上的研究已经取得了很大的进展。黄伟迪等[7]对高速电主轴的轴承预紧力与临界转速的关系进行了研究,发现降低预紧力会使轴承刚度降低,进而使主轴临界转速降低。邵堃等[8]为补偿主轴在转动过程中,轴承对主轴变形的影响,设计了轴承移动轴套。但该装置不可实时控制,导致实际效果并不理想,最大误差为17%。Zhou等[9]提出了一种基于最小均方算法(least mean square,LMS)和影响系数法(influence coefficient method,ICM)的主动磁轴承(active magnetic bearings,AMB)在线不平衡补偿算法,使转子达到一定的动平衡水平。陈鹏等[10]对电主轴切削载荷对主轴振动精度的影响进行了分析,为保证主轴的加工精度,需限制主轴的转速。丁超[11]对电主轴的轴承预紧力对主轴温升和静刚度的影响进行了分析,电主轴性能会随着轴承的预紧力的增大而提高,但温升也会随之增大。陈润霖等[12]为了保证电主轴的回转精度,采用电磁力消减加工力,并初步证明了其可行性。
由上述分析可以得出,目前,在球轴承支撑的电主轴中,通常通过提高轴承预紧力来提高电主轴系统刚度,但轴承的使用寿命会因此降低,这限制主轴临界转速的提高。在磁悬浮电主轴中,虽然磁悬浮轴承无机械磨损,但其动刚度较低,欲提高主轴系统刚度,则需要较为复杂的控制算法。因此,本文提出一种由磁悬浮轴承和角接触球轴承共同支撑的复合支撑电主轴,引入磁悬浮轴承为转子提供部分支撑,适当减小角接触球轴承的预紧力,进而实现在提高主轴系统刚度时,降低球轴承的应力,提高球轴承的使用寿命。因球轴承提供了主要的支撑刚度,弥补了磁轴承动刚度较低的问题,所以磁轴承在不需较为复杂的控制系统时,主轴便可以具有较高的动态刚度。
本文通过ANSYS有限元仿真和振动试验,对球轴承支撑电主轴和磁-球轴承复合支撑电主轴转子的模态、谐响应、振动位移、振动加速度、球轴承应力进行对比分析。
1 磁-球轴承复合支撑电主轴结构及建模
1.1 磁-球轴承复合支撑电主轴样机结构
磁-球轴承复合支撑电主轴样机结构,如图1所示。由内置电机、冷却水套、轴承支撑系统和主轴转子等部分组成。内置电机为三相永磁同步电机,最高转速可达 30 000 r/min。为避免内置电机和轴承系统因工作而产生温度过高现象,在俩处分别设计了水冷系统,并为角接触球轴承设计油气润滑装置降低球轴承磨损,增加其使用寿命。

图1 磁-球轴承复合支撑电主轴样机模型Fig.1 Magnetic bearing and ball bearing composite support spindle prototype model
本文研究的重点在于电主轴的支撑系统,该电主轴分别由一对径向磁轴承、一个轴向磁轴承和两对角接触球轴承组成,为保证各轴承之间的同轴度,在加工阀块时保证各个阀块基准的一致性,确保阀块上的轴承定位孔符合同轴度要求,并通过机床底座上的T型槽和凸台对各个阀块进行定位。其中,球轴承在主轴两侧,采用双联配置形式正安装方式,并且有螺钉-压力传感器装置对球轴承进行预紧,实现对球轴承预紧力的监测与调整。径向磁轴承位于中间,在径向磁轴承侧面放置两个电涡流位移传感器,用来实时检测主轴径向位移变化。轴向磁轴承位于左侧径向磁轴承与电机之间,主要提供主轴的轴向刚度。左端设置一个电涡流位移传感器用来检测转子轴向位移变化,右端使用一个径向磁轴承用来对主轴施加径向外扰力。
1.2 磁-球轴承复合支撑电主轴数学模型
图2为转子受力分析图,磁-球轴承复合支撑电主轴转子可简化为有7个受力点的转子,A、B两点为角接触球轴承受力点,D、E两点为径向磁轴承受力点,F点为轴向磁轴承受力点,C点为集中质量点,G为外扰力作用点。据此可建立如式(1)磁-球轴承复合支撑电主轴的数学模型。
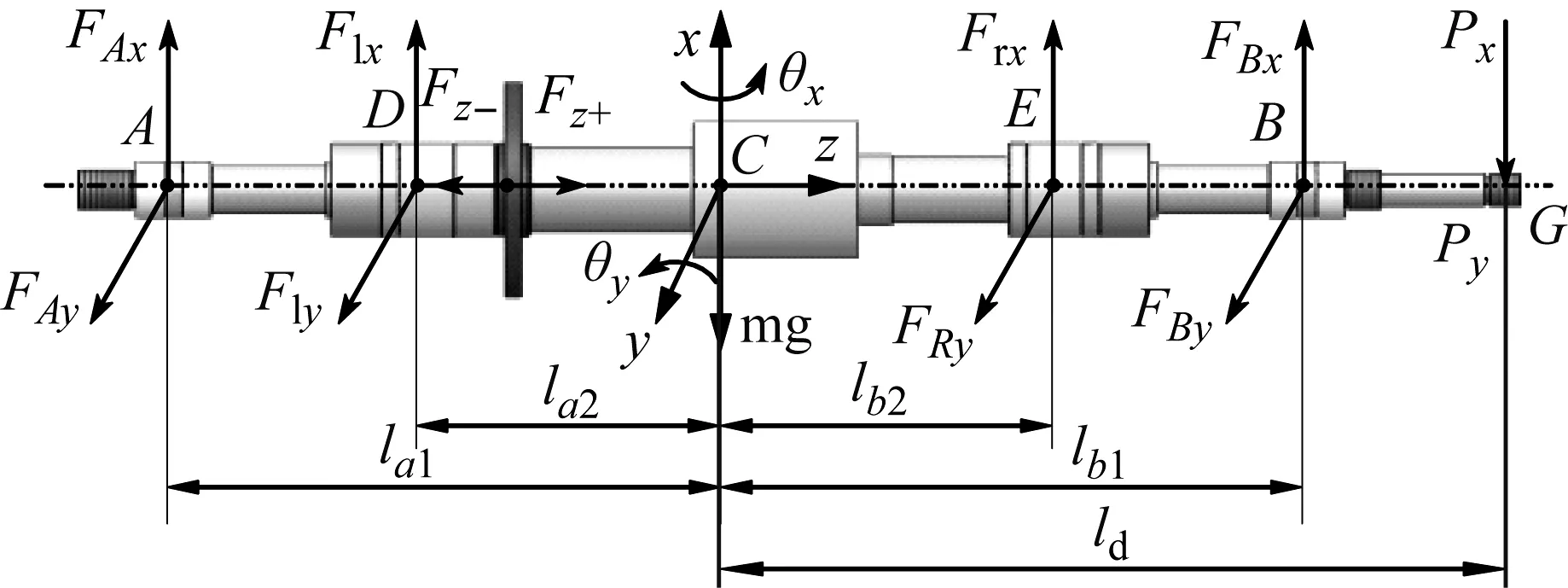
图2 电主轴转子受力分析图Fig.2 Force analysis diagram of motorized spindle rotor
(1)
式中:JP为转轴极转动惯量;Jd为转轴赤道转动惯量;Fl、Fr为磁轴承支撑力;FA、FB球轴承支撑力;Fz为轴向电磁力;fx、fy为离心力;Px、Py为外扰力。
1.3 磁轴承电磁力计算
x、y平面中左右径向磁轴承电磁力计算公式为
(2)
式中:xl、yl、xr、yr分别为左右径向磁轴承偏离平衡位置的位移;kil、kir,kl、kr分别对应磁悬浮轴承的电流和位移刚度。
本文径向磁悬浮轴承由8个磁极构成,工作原理如图3所示,该磁轴承可实现差动控制,1、3两组线圈控制转子y方向移动,2、4两组线圈控制转子x方向移动。其各参数如表1所示。

图3 径向磁轴承原理图Fig.3 Schematic diagram of radial magnetic bearing

表1 径向磁轴承结构参数Tab.1 Structural parameters of radial magnetic bearing
因电磁力方向与磁极方向存在22.5°夹角,所以其位移刚度与电流刚度为
(3)
式中:μ0为空气磁导率;S为磁极面积;N为线圈匝数;I0为偏置电流;δ为气隙;α为力与磁极夹角α=22.5°。
对于PID控制,磁轴承系统刚度不仅与电流刚度和位移刚度有关,还与控制参数有关[13]。如果系统刚度远比位移刚度大,则对闭环控制系统的稳定性很不利,由于复合支撑电主轴由球轴承提供主要支撑,因此转子系统稳定性较高,磁轴承控制器比例增益为100。
1.4 球轴承支撑力计算
(1) 轴承单个滚珠受力分析
电主轴采用7203C角接触球轴承,轴承滚珠受力如图4(a)所示,Fr1、Fr2分别为轴承外圈和内圈对滚珠施加的径向力,与轴承受到的外载有关,Ft为滚珠受到的切向力,其值等于弯矩Mg与滚珠半径之比。Fc为滚珠在滚动时受到的离心力。根据力学平衡方程可得

(a) 轴承滚珠受力分析图
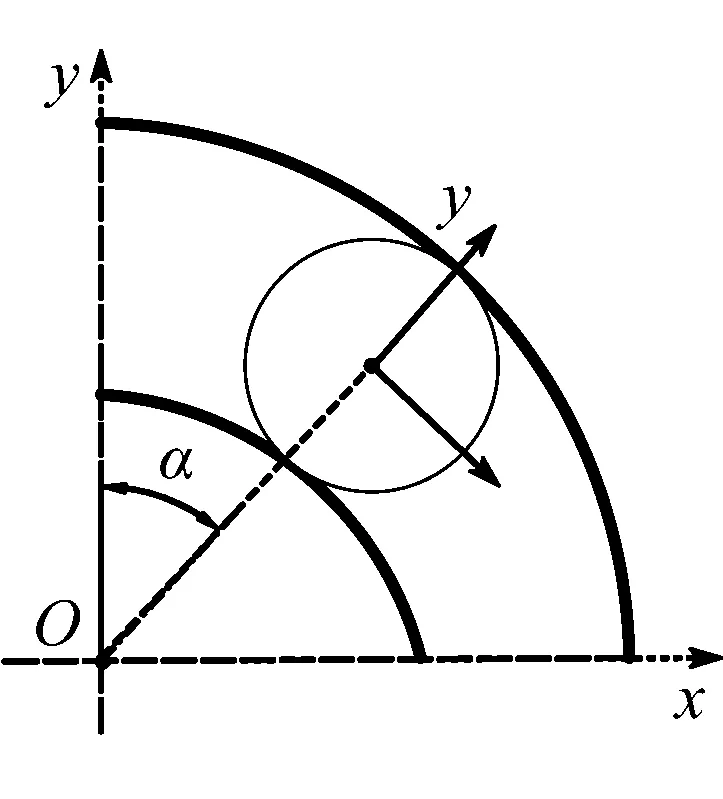
(b) 轴承滚珠位置示意图图4 角接触球轴承受力分析简图Fig.4 Schematic diagram of force analysis of angular contact ball bearings
(4)
其中Fr1、Fr2根据Hertz接触理论可获得接触力与接触变形之间的表达式为式(5),δ1、δ2为接触变形量,k1、k2为接触刚度系数[14]。
(5)
(2) 轴承整体受力分析
图4(b)为轴承滚珠位置示意图,α为滚珠旋转角度,对滚珠受力进行分解可得到
(6)
(3) 轴承刚度计算
通过式(6)可分别求出左右球轴承受力FAx、FAy、FBx、FBy,其中n为滚珠个数,将力代入式(1)中可求得角接触球轴承的位移为xa、ya、xb、yb;根据胡克定律可通过式(7)可求出球轴承支撑刚度kax、kay、kbx、kby。
(7)
1.5 转子偏心质量引起的离心力计算
转子由于材料分布不均、加工和装配误差等原因,会使转子的质心与形心并不重合,存在偏心质量[15-16]。根据国家平衡等级标准,适用于电主轴的标准可分为三个等级:G2.5、G1、G0.4,本文中主轴转子在8 000 r/min时,通过式(8)可获得允许不平衡量范围为2.99~18.74 g·mm。
G=e·ω/1 000
(8)
式中:G为动平衡等级;e为偏心距;ω为角速度。
当转子在高速旋转时会产生离心力,引起转子受迫振动,转速和偏心距越大,这种现象越明显。下面对该现象进行分析。
如图5(a)所示,当转子的质心c与转子的形心o′不重合且偏心距为e,转子以角速度Ω转动时,由质心和形心的关系可得
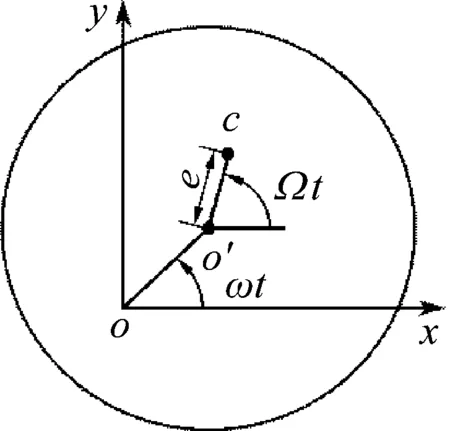
(a) 质心截面示意图

(b) 质心同步进动示意图图5 偏心质量原理图Fig.5 Schematic diagram of eccentric mass
(9)
对时间t求二次导,可得质心c的运动微分方程
(10)
一般情况下,转子的轴承支撑可视为弹性支撑,在轴承弹性支承的作用下,由质心运动定理可得
(11)
将式(8)代入式(7)可得形心的强迫运动微分方程
(12)
其中自然频率ωn=k/m。
为简化计算,将式(9)改写为复变量的形式,则有
(13)
其特解为
s=AeiΩt
(14)
可求得在偏心质量作用下引起的不平衡激振力的响应振幅为
(15)
因此质心o′的不平衡响应为
(16)
由式(13)与式(10)可知,质心o′的振动响应频率与不平衡质量所产生的激振力频率一致,由此可知,坐标原点o、形心o′和质心c三点始终在同一直线运动,运动角速度为Ω,即如图5(b)所示。当进动角速度ω等于自传角速度Ω时,质心与形心做同步进动[17]。且由偏心质量产生的离心力如式(14)所示
(17)
2 电主轴转子模态与振动响应分析
2.1 模态分析
在有限元仿真中,球轴承四个方向的刚度采用四个弹簧接触(Spring)来替代,如图6中位置A和B处所示。磁轴承采用轴承接触(Bearing)来替代,如图6中位置C和D处所示。其中球轴承支撑电主轴的球轴承预紧力为235 N,刚度为1.46×108N/m。复合支撑电主轴的球轴承预紧力为135 N,刚度为1.20×108N/m,磁轴承系统刚度为1.03×107N/m。以此达到降低球轴承应力,提高轴承疲劳使用寿命的目的。

(a) 球轴承支撑电主轴

(b) 复合支撑电主轴图6 不同支撑方式电主轴轴承约束图Fig.6 Bearing constraint diagram of motorized spindles with different support modes
图7为两种不同支撑方式的电主轴前两阶振型图,球轴承支撑电主轴一阶固有频率为268.72 Hz,二阶固有频率为816.14 Hz。磁-球复合支撑电主轴的一阶固有频率为375.88 Hz,二阶固有频率为936.62 Hz。对应一阶临界转速如表2所示。

(a) 球轴承支撑第一阶振型
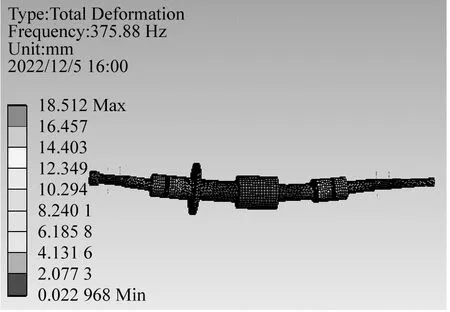
(b) 复合支撑第一阶振型

(c) 球轴承支撑第二阶振型

(d) 复合支撑第二阶振型图7 电主轴前两阶模态振型图Fig.7 The first two mode shapes of the motorized spindle

表2 不同支撑方式的电主轴一阶临界转速对比表Tab.2 First order critical speed comparison table of motorized spindles with different support modes
由表2可知,在球轴承刚度大幅度降低的前提下,复合支撑电主轴比球轴承支撑电主轴在一阶的临界转速提高40%。
2.2 谐响应分析
谐响应分析是在模态分析的基础上,采用模态叠加法进行分析。本节对两种电主轴以主轴在高速旋转时,由不平衡质量所产生的离心力为激振力,对两种电主轴进行谐响应分析,观察其振动响应情况,并进行对比分析。
离心力数值为转子在8 000 r/min匀转速时,在偏心矩为4 μm时产生的离心力,其计算公式为
F=mω2r
(18)
式中:ω为匀速时转子角速度;r为偏心距。
分析电主轴的频率范围为 0~1 200 Hz,分析点取80个,分析在外扰力影响下电主轴的轴输出端和轴中间段的位移振动情况,结果如图8所示。
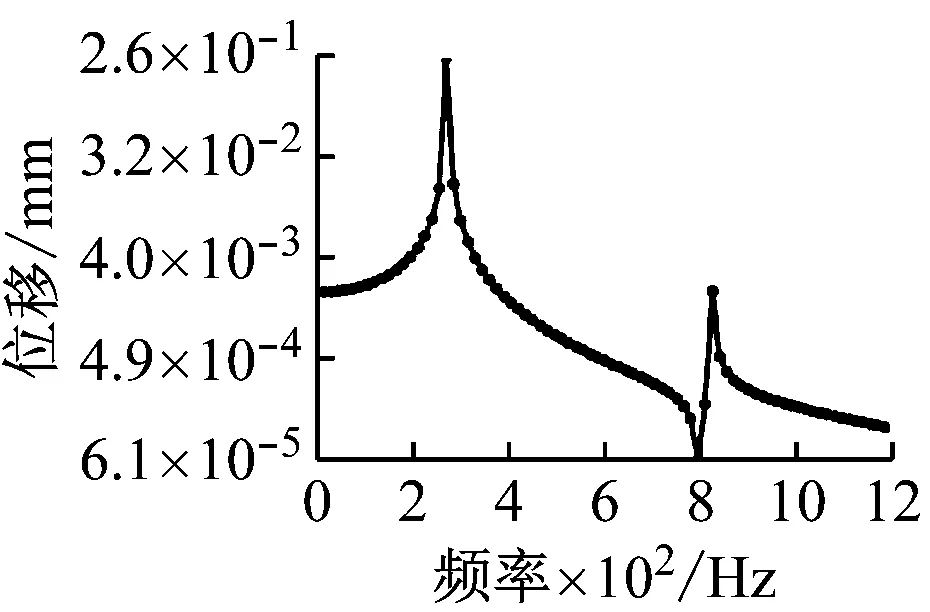
(a) 球轴承支撑轴中段
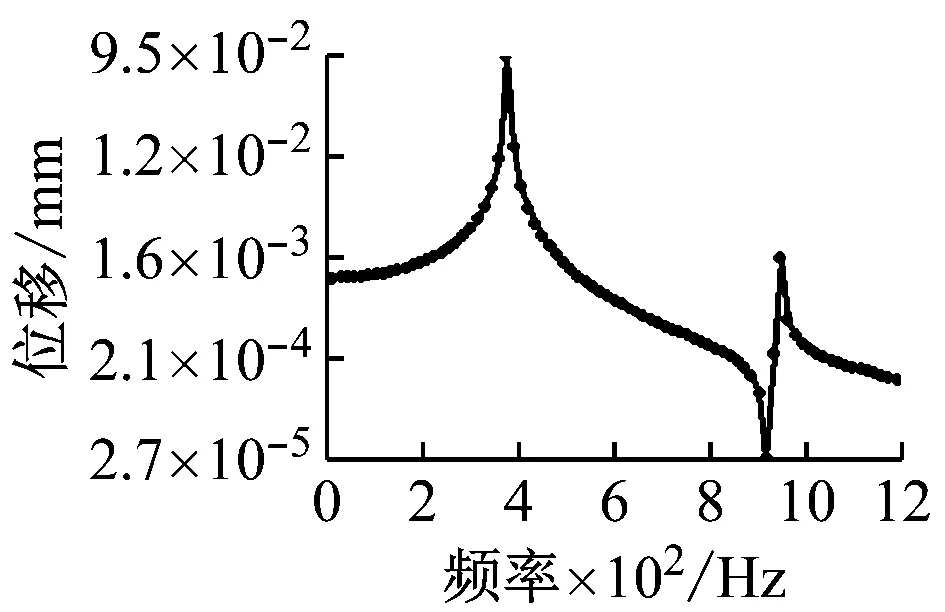
(b) 复合支撑轴中段

(c) 球轴承支撑轴输出端

(d) 复合支撑轴输出端图8 两种电主轴不同位置的谐响应分析图Fig.8 Harmonic response analysis diagram of two motorized spindles at different positions
从图8可知,在低阶频率时主轴振动位移随激励频率变化缓慢,当激励频率达到固有频率附近时,电主轴输出端、中段的振动幅值急剧增加,此时发生共振现象,主轴最大振幅发生在主轴中段,因此电主轴在工作时应避免固有频率附近的工作频率。对比两种主轴谐响应图,如表3所示。
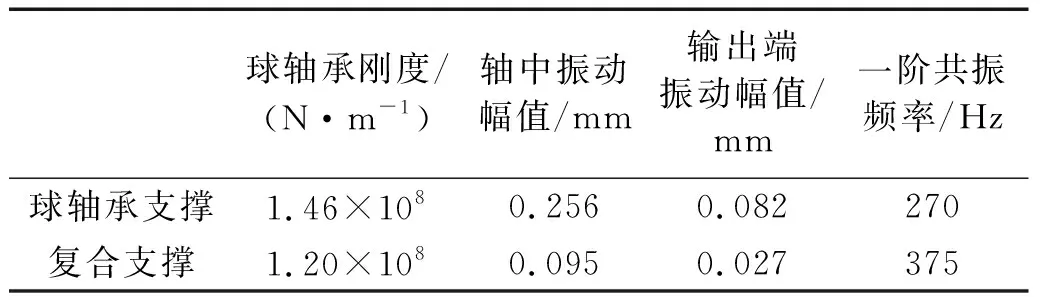
表3 不同支撑方式谐响应振动幅值对比表Tab.3 Comparison table of harmonic response vibration amplitude of different support modes
由表3可知,复合支撑电主轴的共振频率要大于球轴承支撑共振频率,其振动幅值更低,因此复合支撑电主轴在避免发生共振时可达到的极限转速更高。
3 主轴不平衡振动仿真分析
由于材料分布不均、加工和装配误差等原因,转子会存在偏心质量,当电主轴高速运行时,由不平衡质量所产生的振动极其明显,其振动状况直接影响机床加工质量。因此本节针对由不平衡质量对主轴所引起振动进行ANSYS瞬态动力学有限元仿真分析,并对比在只有球轴承支撑与有磁-球轴承复合支撑时的振动响应情况。
3.1 施加约束条件
因本文探究的是电主轴的振动响应与轴承支撑方式之间的关系,所以合理假设转子存在4 μm偏心距,转子转速在0~1 s内匀加速至工作转速8 000 r/min,在1 s后匀速运转。因此主轴在匀加速阶段会受到切向力和离心力,在匀速工作阶段只受到离心力。两阶段在只考虑偏心质量时,受力分析如下
(1) 加速阶段切向力计算
Ft=mat
(19)
式中:m为转子质量6.28 kg;at为质心处切向加速度0.003 35 m/s2。
加速阶段离心力计算
(20)

(2) 因匀速阶段切向加速度为0,因此切向力Ft=0,离心力公式为
Fa=mω2r
(21)
因此转子在x,y轴受力为:
(22)
使用ANSYS Workbench有限元分析软件,将力施加到质心轴段上,在轴承处的轴肩上施加z方向位移约束限制主轴轴向运动,x方向施加重力惯性力,轴承刚度设置与模态分析相同。
3.2 振动响应仿真分析
(1) 电主轴不同位置的振幅对比分析
对球轴承支撑电主轴的输出端和中间段进行振动响应分析,设置分析时间步为0.001 s,分析时间至1.2 s。
图9是球轴承支撑电主轴的中间段与输出端y方向的时间位移振动曲线,从中可以看出,由于偏心质量的存在,在启动加速时主轴位移随着速度的增大而增大,当主轴在1 s时达到额定转速,主轴振幅开始逐渐减小,直至趋于稳定。其中轴中段最大位移为9.006 μm,轴输出端最大位移为0.725 μm,轴中段位移远大于轴输出端位移。
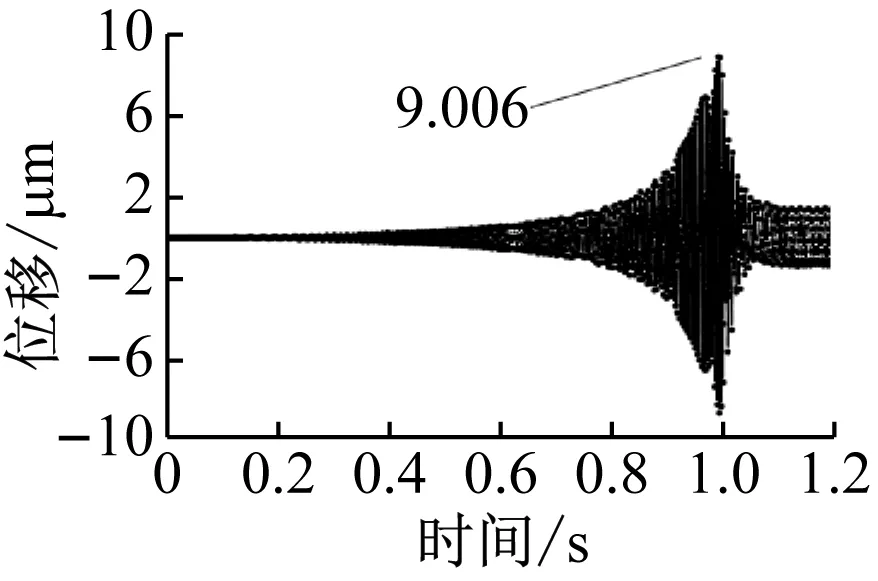
(a) 主轴中段

(b) 主轴输出端图9 球轴承支撑电主轴y方向振动位移Fig.9 Vibration displacement in y direction of Motorized spindle supported by ball bearing
(2) 主轴不同方向的位移对比分析
分别对球轴承支撑电主轴输出端x、y方向振动位移进行仿真分析,仿真结果如图10所示。

(a) x方向

(b) y方向图10 主轴输出端不同方向振动位移Fig.10 Vibration displacement of spindle end in different directions
由图10可知,x方向由于重力的作用,起始时输出端位移波动较大,处于不稳定状态,稳定后,因不平衡质量产生的振动会以重力产生的位移为平衡点波动。且x方向的最大振动幅值为0.803 μm,大于y方向的最大振动幅值0.725 μm,由此可以判断输出端运动轨迹为椭圆,这种现象是由x方向重力加速度产生的。
(3) 加速时不同支撑方式电主轴振动位移和振动加速度对比分析
分别分析球轴承支撑与复合支撑电主轴的轴中段及轴输出端y方向振动位移如图11所示,振动加速度如图12所示。

(b) 复合支撑轴中段

(c) 球轴承支撑输出端

(d) 复合支撑输出端图11 两种电主轴各位置振动位移Fig.11 Vibration displacement at each position of the two motorized spindles

(a) 球轴承支撑轴中段

(b) 复合支撑轴中段

(c) 球轴承支撑输出端

(d) 复合支撑输出端图12 两种电主轴各位置振动加速度Fig.12 Vibration acceleration at each position of the two motorized spindles
与球轴承支撑电主轴相比,将复合支撑电主轴的球轴承刚度降低至1.20×108N/mm时,由图11可知,因磁轴承的介入,复合支撑电主轴的轴中段与输出端的振动位移幅值均有所降低,分别降低了70%和77.2%。由图12可知,复合支撑电主轴的轴中段与输出端的振动加速度均有所降低,分别降低了68.4%和77.4%。
(4) 稳态时不同支撑方式电主轴振动位移和振动加速度对比分析
表4为1 s后主轴匀速转动时,球轴承支撑电主轴和复合支撑电主轴由不平衡质量引起的振动位移幅值对比表。据此可知,稳态时复合支撑比球轴承支撑电主轴的振动位移幅值至少降低32.1%。

表4 稳态时电主轴的各位置x、y方向位移值Tab.4 The displacement value in x and y directions of each position of the motorized spindle in steady state
表5为1 s后主轴匀速转动时,球轴承支撑电主轴和复合支撑电主轴由不平衡质量引起的振动加速度幅值对比表。据此可知,稳态时复合支撑比球轴承支撑电主轴的振动加速度至少降低33.9%。

表5 稳态时电主轴的各位置x、y方向加速度值Tab.5 The acceleration value in x and y directions of each position of the motorized spindle in steady state
由振动位移和振动加速度仿真结果可知,复合支撑电主轴有磁轴承参与支撑,可对转子位移进行主动控制,因此,复合支撑电主轴的轴中段和轴输出端的振动位移和振动加速度幅值要比球轴承支撑电主轴小,可有效抑制主轴振动,提高主轴动态刚度。
3.3 球轴承应力仿真
对两种支撑方式的电主轴球轴承施加所受到的载荷,复合支撑和球轴承支撑电主轴的球轴承轴向载荷分别为上述的轴承预紧力135 N和235 N,径向载荷为上述不平衡质量产生的离心力,其计算公式为式(14),使用ANSYS静力学模块对其进行应力分析。
图13为不同支撑方式的电主轴中球轴承应力云图,球轴承支撑电主轴的球轴承受到的最大应力为9.47 MPa,复合支撑电主轴中球轴承最大应力为5.43 MPa,最大应力降低42.6%。降低球轴承接触应力可有效提高轴承疲劳寿命[18]。

(a) 球轴承支撑

(b) 复合支撑图13 两种电主轴中球轴承应力云图Fig.13 Stress cloud diagram of ball bearing in two motorized spindles
4 电主轴振动实验
为验证磁-球轴承复合支撑电主轴比球轴承支撑电主轴的振动特性更好,分别对当转速为1 000 r/min,2 000 r/min,3 000 r/min时的两种支撑方式的电主轴进行振动实验,磁-球轴承复合支撑电主轴试验平台与电气控制部分,通过变频器控制电主轴转速,采用电涡流位移传感器检测转子振动位移,如图14所示。

(a) 主轴试验样机

(b) 电气控制部分图14 磁-球复合支撑电主轴试验平台Fig.14 Test platform of magnetic bearing and ball bearing composite supported motorized spindle
为了方便观察在不同转速下的磁轴承介入前后电主轴的振动效果,将磁-球轴承复合支撑电主轴和球轴承支撑电主轴的振动位移进行对比,如图15所示。

(a) 1 000 r/min

(b) 2 000 r/min

(c) 3 000 r/min图15 两种电主轴不同转速下振动位移对比Fig.15 Comparison of vibration displacement of two motorized spindles at different speeds
由图14可知,在电主轴转速为1 000 r/min时,球轴承支撑电主轴转子的振幅为1.25 μm,磁-球轴承复合支撑电主轴转子的振幅为0.875 μm,在磁轴承参与支撑后,电主轴转子的振动幅值降低了30%。当转速为2 000 r/min时,球轴承支撑电主轴转子的振幅为1.35 μm,磁-球轴承复合支撑电主轴转子的振幅为1.125 μm,振幅降低了16.6%。当转速为3 000 r/min时,球轴承支撑电主轴转子的振幅为1.45 μm,磁-球轴承复合支撑电主轴转子的振幅为1.15 μm,振幅降低了20.6%。
由此可以看出,由于不平衡质量的存在,电主轴振动幅值会随着转速的提高而增大,在磁轴承的作用下,复合支撑电主轴的振动幅值要低于球轴承支撑电主轴的振动幅值16.6%以上,具有较好的抗振能力。
5 结 论
本文为提高电主轴系统刚度和抗振能力,提出磁-球轴承复合支撑电主轴结构,通过ANSYS模态仿真、谐响应仿真、瞬态动力学仿真、振动实验,与球轴承支撑电主轴作对比分析。可得出以下结论:
(1) 模态和谐响应仿真分析结果表明:与球轴承支撑电主轴相比,将复合支撑电主轴的球轴承刚度由1.46×108N/mm降低至1.20×108N/mm时,复合支撑电主轴的临界转速得到提高,振动响应幅值大幅度降低。
(2) 瞬态动力学仿真分析结果表明:当主轴转子存在4 μm偏心距的不平衡量,在0~1 s内启动至8 000 r/min,1 s后匀速运行时,复合支撑电主轴的比球轴承支撑电主轴的振动位移幅值降低了32.1%以上,振动加速度幅值降低了33.9%以上,球轴承最大应力降低42.6%。
(3) 电主轴空载振动实验结果表明:当主轴转子因存在不平衡质量而产生振动时,磁-球轴承复合支撑电主轴要比球轴承支撑电主轴的振动幅值小16.6%以上,可有效抑制振动。

