基于改进粒子群算法飞机总体方案优化设计方法

史志富,王世杰,刘伟明

(西安航空学院 飞行器学院,西安 710077)

0 引言

在飞机总体设计过程中,飞机总体参数如飞机重量、发动机推力、气动外形参数等是飞机总体设计的重要内容[1]。这些参数的计算通常涉及气动力计算、质量估算、性能计算等多个专业,这些专业模块中涉及的参数众多,而且这些参数之间相互嵌套构成耦合关系,形成一个复杂的非线性方程。目前飞机总体参数设计常用的方法包括解析法、类比法、优化法等,其中解析法是对建立的数值模型进行精确的解析求解[2-4],其特点是计算精确,但是计算难度大,通常只能获取少量的可行解;类比法是根据历史设计数据,考虑飞机之间的相似性,通过类比的方法近似确定一组参数,然后进行模型验证[5-6],该方法效率低,需要反复迭代进行;优化法是近年来研究较多的方法,主要是采用遗传算法、模糊优化算法、进化计算等对设计问题进行优化[7-11]。优化法对于求解非线性问题具有一定的优越性,它能够基于一定的设计目标,建立总体设计的优化模型和约束条件,然后利用优化算法进行自动寻优。

在进化计算中,粒子群算法作为一种群体协作搜索算法,通过模拟鸟类觅食行为,可用于大搜索空间的优化问题。由于采用了群智能协同机制,使得它具有并行处理、鲁棒性好、易于实现等特征[12-14]。相对于传统的遗传算法等优化算法,它没有遗传算法复杂的交叉和变异操作,原理简单,参数较少,容易实现。鉴于此,对飞机总体设计非线性方程采用埃特金加速法进行迭代求解,然后将设计目标和设计要求转化为优化模型,利用改进PSO算法进行优化求解,可解决飞机总体方案的优化求解问题。

1 飞机改型方案优化问题

1.1 设计问题描述

飞机方案优化设计问题通常可以描述成如下的非线性约束规划问题:

求设计变量X=(X1,X2,…,Xn);

使目标函数Y1→min(max);

满足约束条件YiReai(i=2,3,…,m)。

Re表示Yi与ai之间的关系,可以为=、≤或≥。Y=(y1,y2,…,ym)为方案的各项指标。对于某型改型飞机,根据技术指标要求,确定各项技术指标为航程、有效载荷、起飞滑跑距离、着陆滑跑距离;约束函数要求最小的起飞重量、最大航程、大的有效载荷、较短的起飞与着陆滑跑距离、失速速度不得超出一个允许的最大失速速度,使飞机有较好的失速特性。所要求的设计变量为机翼面积、平尾面积、垂尾面积、机身长度、巡航高度空气密度与巡航速度。将飞机起飞总重量最小作为优化目标,即在使得约束条件满足一定指标的条件下,使得飞机起飞总重量越小越好。然后将其它的指标如航程、有效载荷、起飞和着陆滑跑距离、失速速度作为约束条件进行处理。由此可得飞机总体参数设计的优化模型如下:

minWdg(X)

(1)

(2)

其中:X=(Sw,Shw,Svw,Lf,ρc,Vc),分别表示机翼面积、平尾面积、垂尾面积、机身长度、巡航高度空气密度与巡航速度;Wdg(X)为飞机总重量;R为航程;STOG为起飞滑跑距离;SL为着陆滑跑距离;Vs为失速速度;Wload为有效载荷。

1.2 设计问题分析

由于所要优化参数包括重量、性能外形、气动等专业内容,外形影响飞机的气动特性,气动参数影响飞机的性能,重量影响飞机的气动和性能,各专业之间存在耦合关系,专业飞机总重和空重又存在迭代关系。整个优化问题十分复杂,在方案设计阶段,为简化问题,常采用经验公式建立模型。

1.2.1 重量分析计算

飞机起飞总重为空机重量、燃油重量和有效载荷重量之和。空机重量又为结构、起落架、动力系统和设备系统四部分之和。各部分计算公式描述如下:

飞机总重量

Wdg=W空重+Wfw+Wload

(3)

其中:

W空重=W结构+W起落架+W动力+W设备

(4)

W结构=W机翼+W平尾+W垂尾+W机身

(5)

W起落架=W前起+W主起

(6)

W动力=W发动机+W燃油系统

(7)

W设备=W飞控+W液压+W电气+W电子+W空调和防冰

(8)

(9)

(10)

(11)

(12)

W主起=0.128 6(N1W1)0.768(Lm/12)0.409

(13)

W前起=0.242(N1W1)0.566(Ln/12)0.845

(14)

(15)

(16)

(17)

W液压=0.001Wdg

(18)

W电气=8.533 1(W燃油系统+W电子)0.51

(19)

(20)

(21)

其中:Aw为机翼展弦比;A平尾为平尾展弦比;A垂尾为垂尾展弦比;t/c为相对厚度;λ为稍根比;λht为平尾稍根比;λvt为垂尾稍根比;Bw为机翼翼展;D为机身直径;Lm为主起落架长度;Ln为前起落架长度;Lt为尾力臂;Ma为马赫数;Nen为发动机数目;N1为极限过载;Nt为油箱数目;Np为载人数目;Nz为极限过载;Q为巡航时的动压;Sf为机身侵湿面积;Wen为单台发动机重量;Wfw为燃油重量;Wfc为巡航燃油重量;Wpress为气密引起的重量增加量;Wuav为装机电子设备重量;Λ为机翼后掠角;Λht为平尾后掠角;Λvt为垂尾后掠角;ΛLE为机翼前缘后掠角。

1.2.2 起飞、着陆性能分析计算

起飞滑跑距离STOG是指从飞机打开刹车,从静止状态开始滑跑,到飞机的所有机轮全部离开地面这段时间内,飞机所经过的距离。该段距离通常可分为两部分,一部分是飞机从零速度开始滑跑到飞机前轮离开地面所经过的距离,定义为SG;另一部分是飞机从前轮离开地面到所有机轮离开地面所经过的距离,定义为SR。即:

STOG=SG+SR

(22)

其中:SG的计算公式:

(23)

其中:

KT=T/Wdg-μ

(24)

(25)

其中:T为推力;μ为地面滚动摩擦因子;VTO为起飞速度;ρc为设计参数巡航高度空气密度。

SR的确定:由于飞机从抬前轮到起飞完成所用时间主要取决于飞机驾驶员。对于大型飞机来说,其典型值一般为3 s,由此SR可近似等于3VTO;

着陆滑跑距离的计算公式为:

(26)

其中:Vs为飞机的失速速度。

1.2.3 航程性能分析

飞机航程的计算可依照布列盖(Breguet)航程公式,求解过程中需要知道飞机的升阻比(L/D)。

(27)

其中:

Swet=Sf+2Sw+3×(0.2Sw)

(28)

此时,航程计算公式如下:

(29)

其中:η为发动机效率;c为发动机耗油率。

1.2.4 失速速度分析计算

飞机的失速速度是影响飞机安全的主要因素。失速速度直接由翼载和最大升力系数确定,计算公式如下:

(30)

1.3 设计问题的快速求解

在飞机重量设计问题中,设计重量既是自变量又是因变量,故飞机重量方程是典型的非线性方程x=φ(x)。

对于该非线性方程的求解,一般采用近似求解方法,其中埃特金(Aitken)加速迭代法是一种常用的快速求解方法。

设非线性方程为:

x=φ(x)

(31)

取初值x0,埃特金迭代一次的过程如下:

预报:

u=φ(xk)

(32)

再预报:

v=φ(u)

(33)

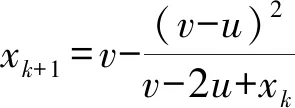
(34)

结束迭代过程的条件为:

|v-u|<ε

(35)

此时,v为非线性方程的一个实根,ε为预先给定的精度要求。

2 基于改进粒子群算法的优化设计

2.1 粒子群优化算法

粒子群算法(Particle Swarm Optimization,PSO)是美国学者Eberhart R C和Kennedy J在1995通过观察模拟鸟群、鱼群捕食行为提出的一种进化计算方法,该方法同遗传算法、蚁群算法等进化算法一样,属于群体优化算法。其特点是每个粒子个体都像鸟或鱼一样具有一定的运动速度,可以在有限空间内自由移动,在移动过程中每个个体可以记住自身的最佳位置,群体之间通过合作和竞争获得群体的最佳位置,然后通过二者之间的差来调整自身的位置和速度,使得群体最终达到最优,其模型如下:

设粒子数量为N,粒子的维数为L,单个粒子的位置区间为[xd min,xd max](d=1,2,…,L),单个粒子的速度区间为[vd min,vd max](d=1,2,…,L),首先通过初始化得到具有一定位置和速度的N个粒子,然后分别计算优化函数的适应度值,得到每个个体的最佳位置和群体的最佳适应度;然后进入循环迭代,根据个体粒子i在第t+1次迭代时的个体极值pid(t)和全局极值Pgd(t)来更新自己的速度和位置。粒子群算法的速度更新模型如下:

vid(t+1)=vid(t)+c1r1(pid(t)-xid(t))+c2r2(pgd(t)-xid(t))

(36)

粒子群算法的位置更新模型如下:

xid(t+1)=xid(t)+vid(t+1)

(37)

其中:vid(t)为第t次迭代时第i个粒子第d维的速度;xid(t)为第t次迭代时第i个粒子第d维的位置;c1为自我学习因子;c2为社会学习因子;r1、r2为[0,1]上的两个均匀分布的随机数。

2.2 粒子群算法的改进

2.2.1 搜索平衡能力的改进

由(36)式可知,下一时刻粒子的速度由当前的速度“惯性”、粒子的“自我”认知以及粒子向其它粒子学习的“社会”认知三部分组成。惯性部分是衡量当前速度对下一时刻速度的影响,为改善粒子的“惯性”,增加粒子的多样性,常用的方法是引入惯性权重来平衡粒子的局部搜索能力和全局探索能力,加入惯性权重的速度更新公式如下:

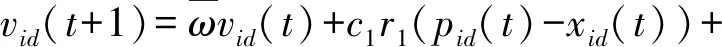
(38)

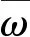
(39)

2.2.2 学习因子的改进

学习因子c1、c2分别表示粒子个体的自我“认知”学习和群体的“社会”学习。通常在初期需要更加关注自我认识能力,在后期则需要关注个体获取社会信息的能力。二者之间通常要求满足c1+c2=4,由此,可建立学习因子的自适应调整规则如下:

(40)

为在初期加快搜索速度,扩大全局搜索范围,快速定位最优值所在局部区域,在后期能在局部区域内进行精准搜索,以较大的概率收敛到全局最优解,对c1,可设cstart=2.5,cend=1.5;对c2,有cstart=1.5,cend=2.5,此时c1、c2满足c1+c2=4。

2.3 优化设计模型的改进

在某型飞机改型设计中,飞机总体参数设计的优化模型是一个多约束优化。但是PSO算法仅能用来处理无约束优化问题,对此需要将多约束优化问题转化为无约束优化问题。转化方法是采用罚函数法,即将约束条件作为惩罚项加入到目标函数中,当不满足约束条件时,给目标函数赋予一个较大的惩罚值,从而使得该值不可能被保留下来,从而达到淘汰对应设计参数值的目的。通过罚函数法可将飞机总体参数优化模型转换成如下的无约束优化模型:

(41)

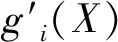
(42)

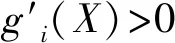
2.4 基于PSO的飞机优化设计流程

结合PSO算法与飞机设计参数优化模型,可得基于PSO的飞机优化设计流程如图1所示。

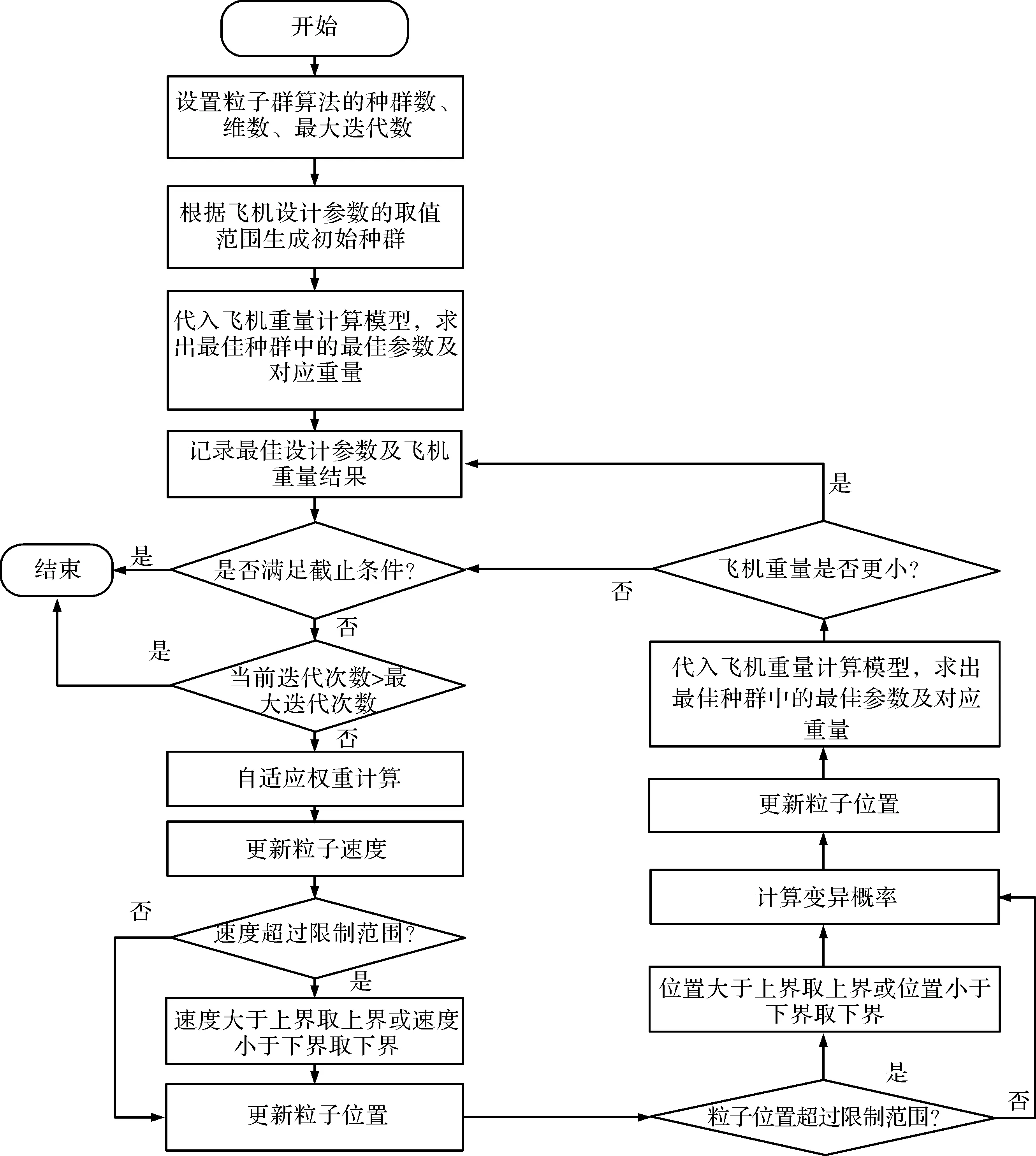
图1 基于PSO的飞机优化设计流程图

步骤1 设置粒子群优化算法的主要参数,如粒子种群数,粒子维数(设计变量个数),最大迭代次数等;

步骤2 根据设计参数的取值范围,随机生成初始化粒子群体的位置和速度;

步骤3 将初始化粒子群体中的每个粒子(一组设计参数)代入飞机重量计算模型公式(3),计算每组设计参数对应的飞机重量;

步骤4 从中计算出当前种群中的最佳设计参数和最小的重量作为粒子群体的全局最优解和最优值,将每个粒子对应的设计参数和重量值作为个体最优解和个体最优值;

步骤5 根据公式(39)和公式(40)计算粒子的惯性权重和学习因子;

步骤6 根据公式(37)、公式(38)来更新每个粒子的位置和飞行速度,并根据粒子位置和速度的区间范围对其位置和速度进行限定;

步骤7 将新的粒子代入飞机重量计算模型公式(3)计算每个粒子的适应值;

步骤8 对每个粒子,将其适应值与个体极值进行比较,如果较优,则更新当前的个体极值;与全局极值进行比较,如果较优,则更新当前的全局极值;

步骤9 判断是否达到预先设定的停止准则或达到最大迭代次数,若为否则返回步骤5,否则停止计算。

3 仿真计算与分析

利用PSO算法对某型飞机改型方案进行综合优化设计。取微粒种群为30,惯性权重随迭代次数从0.9递减到0.4,最大进化代数为200。因为设计变量共有机翼面积、平尾面积、垂尾面积、机身长度、巡航高度空气密度与巡航速度6个,所以粒子的维数设置为6,每个粒子每个维的最大值取相应设计变量的上限值,每个粒子每个维的最大速度为相应设计变量上限与下限之差,参数综合优化结果如表1所示。

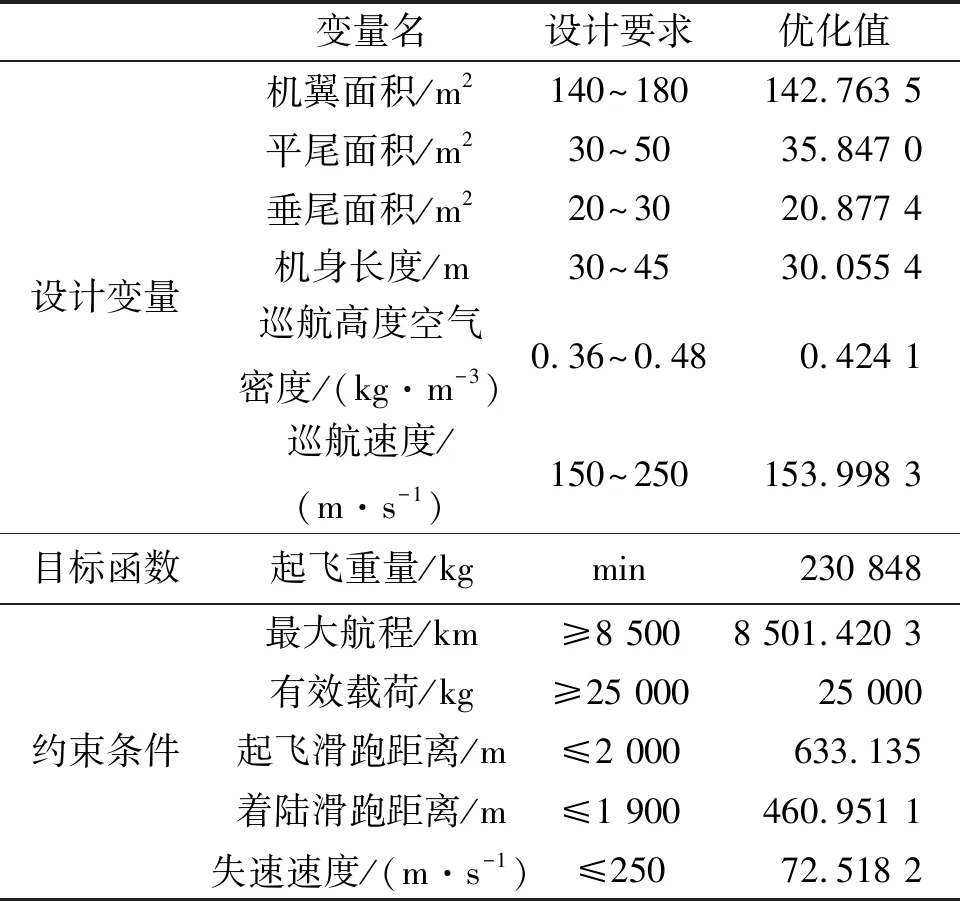
表1 参数综合优化结果

粒子群算法优化过程中,重量随遗传代数的变化过程曲线图如图2所示。

图2 重量随遗传代数的变化过程曲线图

由上图可以看出,随着粒子群算法迭代代数的增加,飞机总体的质量随之逐渐降低,说明粒子群算法能够使得飞机重量朝着最小化方向进化。在寻优过程中,存在着飞机重量持续保持不变的现象,说明飞机的重量设计存在着多个极点,在其过程中粒子群算法陷入了局部最优。但是多次迭代之后,飞机的重量会突然降低一个等级,说明经过粒子群自我学习和群体学习因子等作用,粒子群算法能够跳出局部最优朝整体最优方向发展。

在粒子群优化过程中,随着进化过程的迭代,飞机重量最小对应的最优解也发生相应的变化。设计参数随遗传代数的变化过程曲线图如图3所示。从设计参数的变化过程可以看出,设计参数与飞机重量均有关系。其中机翼面积、平尾面积、垂尾面积对飞机重量影响较为显著,其变化趋势与重量变化趋势基本一致。机身长度直接制约着飞机的重量,所以在优化过程中,机身长度基本取了设计参数下限,且变化范围很小,说明要降低飞机的重量必须在飞机设计时尽可能减少飞机的机身长度。巡航高度空气密度与巡航速度虽然在重量突降的时刻也伴随着突降,但是突降过后也都有上升趋势,并且大部分维持了平稳状态,说明巡航高度空气密度与巡航速度虽然与重量有一定的关系,但是其主要影响的是飞机发动机的耗油率,其对飞机重量的直接影响程度较低。

图3 设计参数随遗传代数的变化过程曲线图

为考察改进粒子群算法的性能,假设惯性权重分为取固定值与采用自适应权重两种方式,权重参数综合优化结果表如表2所示。

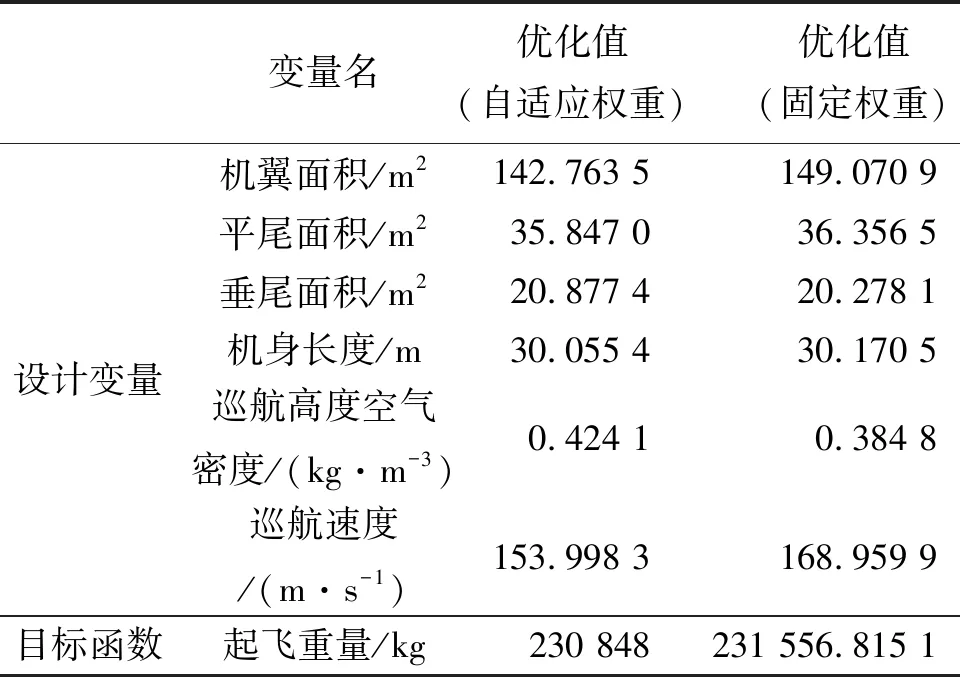
表2 权重参数综合优化结果表

从优化结果可以看出,固定权重条件下粒子群算法仍然能够获得满足约束条件的设计参数,只是自适应权重和学习因子条件下获得的最终的优化结果值更优。这说明自适应权重在收敛率、收敛速度和收敛稳定性上更具有优势。

4 结论

飞机总体方案设计模型是一个复杂的非线性模型,传统的数值解法计算量大、计算次数多,仅能获得局部最优的可行解,难以获得满意的全局最优解。本文提出的基于粒子群算法和埃特金数值算法相结合的飞机总体方案设计优化方法显示出潜在的优势。通过实例仿真分析,该方法在改进粒子群算法性能的同时,实现了飞机总体方案的优化。然而,需要注意的是,该方法仍然需要进一步的实证研究,以评估其在不同情况下的适用性和可靠性。此外,还可以进一步探索如何解决局部最优问题,并扩展该方法到其他领域的总体方案设计中。