基于热传导模型的高温作业专用服装设计研究

周 千

(西安航空学院 理学院,西安 710077)

0 引言

长期在高温环境下工作的人,为避免外界热传导、热辐射、热对流,需要穿着热防护服以降低高温伤害。因此,热防护服必须具有较好的阻止和减缓热量传递的性能[1]。热防护专用服装通常由三层织物材料构成,分别记为I、II、III层,其中I层与外界环境接触,III层与皮肤之间还存在空隙,将此空隙记为IV层,如图1所示。

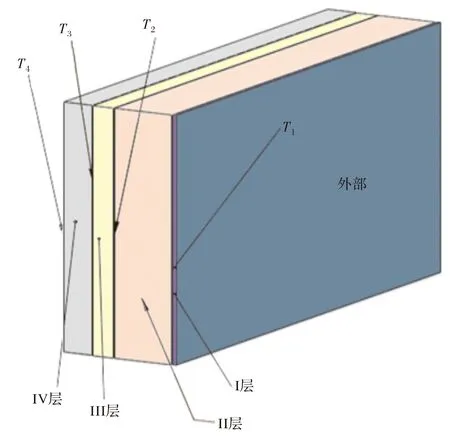
图1 三层防护服示意图

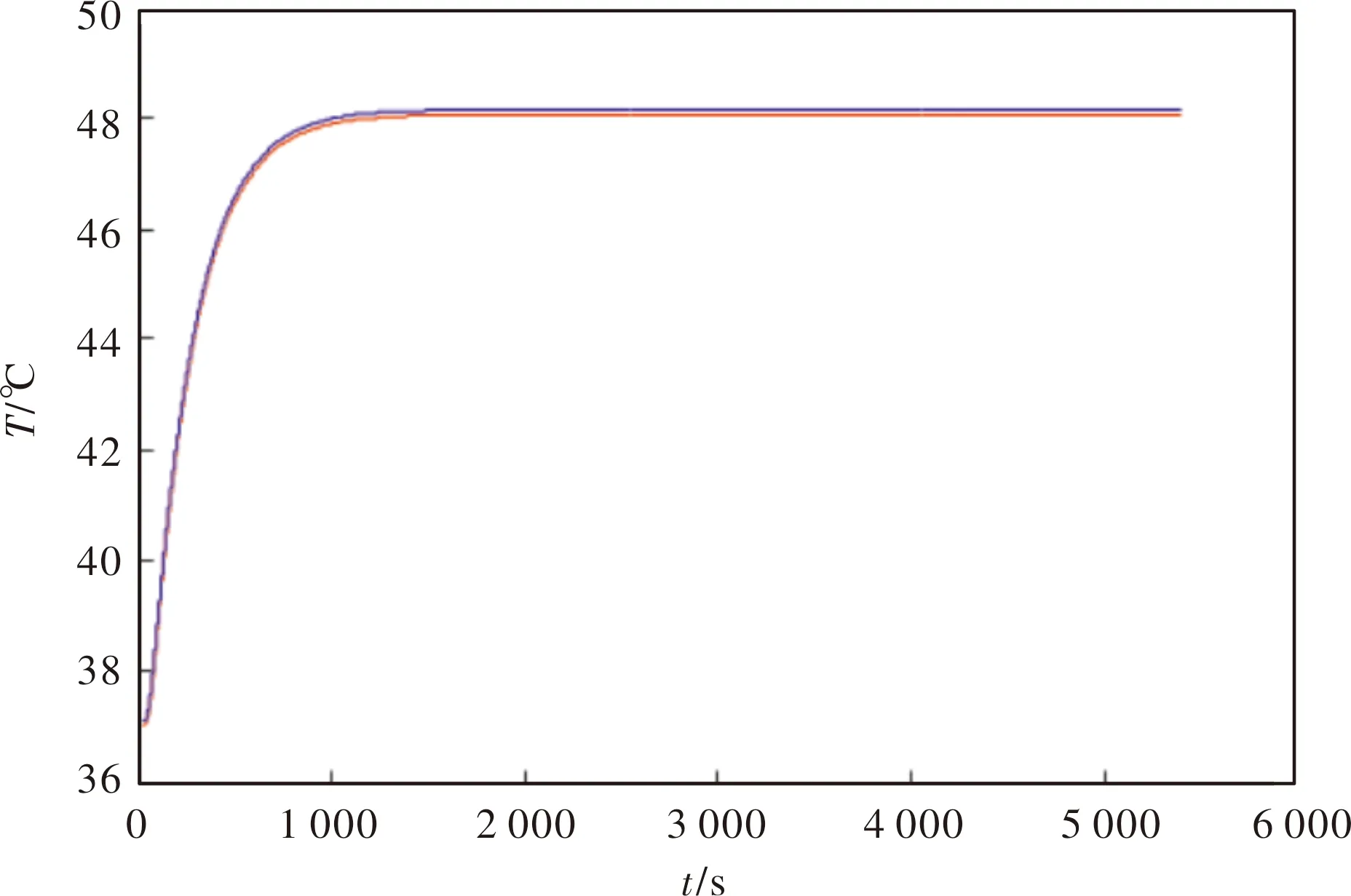
图2 假人皮肤外侧温度拟合曲线

为设计热防护专用服装,可采取试验的方法:将体内温度控制在37 ℃的假人放置在高温环境中,在穿热防护服的条件下测量假人皮肤外侧的温度。试验的方法周期长、成本高。建立适用的数学模型是降低热防护服研发成本、缩短研发周期的有效途径。建立的数学模型应能确定假人皮肤外侧的温度变化情况。考虑实际情况,本文考虑如下条件:(1)当环境温度为65 ℃、IV层的厚度为5.5 mm时,确定II层的最优厚度,确保工作60 min时,假人皮肤外侧温度不超过47 ℃,且超过44 ℃的时间不超过5 min;(2)当环境温度为80 ℃时,确定II层和IV层的最优厚度,确保工作30 min时,假人皮肤外侧温度不超过47 ℃,且超过44 ℃的时间不超过5 min。在满足上述条件下,探讨相关问题,基于热传导理论和实测温度,建立热防护服设计的数学模型,建立的模型能够计算温度分布,旨在为热防护服的设计提供借鉴和参考。

1 基于差分法对假人皮肤外侧的温度进行预测

1.1 高温作业专用服材料的热传递模型建立

假设如下的变量

T1:第I层与第II层交界处的温度;

T2:第II层与第III层交界处的温度;

T3:第III层与第IV层交界处的温度;

T4:假人皮肤外侧温度。

建模采用隔热防护服的结构为三层防护服(图1)。根据引言中的要求,需要得到同一时间不同点的温度及同一点在不同时间的温度。

根据比热容公式[2]

(1)

式中:Q为热量;m为质量;T为温度,有

Q=cmΔT

(2)

所建模型主要解决的是非稳态过程中的热传导问题,故引入导热基本方程式(傅立叶方程)

(3)

式中:λ为热传导系数;A为面积。质量可由下式确定

m=ρV=ρAx

(4)

式中:ρ为密度;V为体积。考虑高温作业专用服装单位面积的导热情况,由式(2)～(4)可得

(5)

式中,t为时间。式(5)两边同时对求偏导得一维热传导方程

(6)

式(6)对于图1中热防护服的Ⅰ、Ⅱ、Ⅲ层都适用。对于IV层(空气层),考虑到厚度小,无对流现象,而它所处在层内亦可忽略热辐射,所以在本文中IV层空气层也可用方程(6)进行计算其中的热传导。

经过上述的分析,可以建立起四层不同材质的热传导方程[3-4],第Ⅰ层的表面温度始终保持在75 ℃,第Ⅰ层传导结束时的温度即是第Ⅱ层开始的温度,第Ⅱ层传导结束时的温度即是第Ⅲ层开始的温度,第Ⅲ层传导结束时的温度即是第IV层开始的温度,由此有

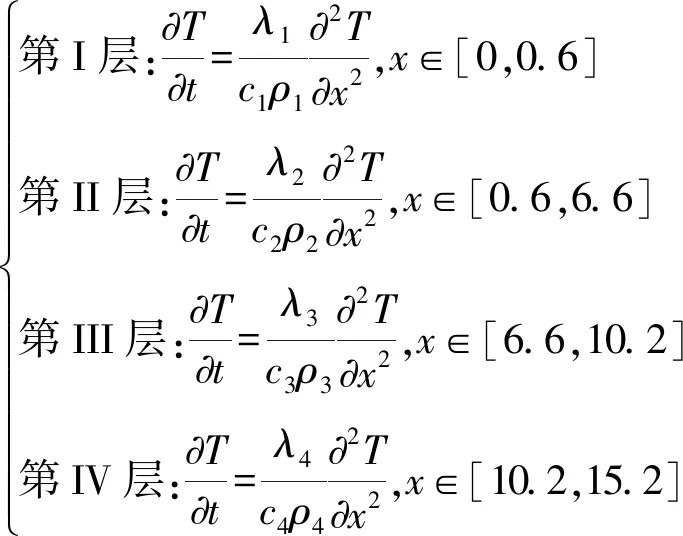
(7)

1.2 高温作业专用服材料的热传递模型求解

对于1.1中建立的模型,利用有限差分法来求解[5]。每一层都需要用有限差分法单独求解(最后再将结果合在一起),单层的求解模型如下:

(8)

将t、x离散化

(9)

采用向前差分格式

(10)

化简有

(11)

可以得到下面的差分方程组

第Ⅰ层材料的求解情况

(12)

第Ⅱ层材料的求解情况

(13)

第Ⅲ层材料的求解情况

(14)

第IV层材料的求解情况

(15)

每一层的N、M取值根据材料的c、ρ以及各自厚度不同也相互不同。利用MATLAB软件来求解上述的差分方程式,并给出假人皮肤外侧温度与程序所得数据拟合曲线如2所示。

发现二者趋势基本一致,吻合较好。

2 条件(1)的模型建立与求解

2.1 建立高温作业专用服材料中间层厚度参数

考虑服装重量和制作成本的条件下,改变第Ⅱ层的厚度,测得皮肤外侧的温度变化,则在符合约束条件的情况下第二层的厚度最小为

d2=min(dx)

(16)

约束条件如下

(1)上述的目标函数需要用上一问的模型带入,第IV层的厚度d4=5.5 mm,外部环境的温度T=65 ℃,工作的时间t=3 600 s。

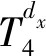
(17)

(18)

(3)第Ⅱ层的厚度满足

0.6≤dx≤25

(19)

综上,第Ⅱ层的厚度的合理模型为

(20)

2.2 高温作业专用服材料中间层厚度参数求解

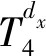
根据上模型(20),利用MATLAB软件进行求解。解得d2=15 mm。

3 条件(2)的模型建立与求解

3.1 建立高温作业专用服材料Ⅱ层IV层厚度参数模型

由于考虑服装重量和制作成本的条件下,改变第Ⅱ层的厚度dx,第IV层的厚度dy,测得皮肤外侧的温度变化T4,则在符合约束条件的情况下第二层的厚度最小为:

d2=min(dx),d4=min(dy)

(21)

约束条件如下:

(1)上述的目标函数需要用上一问的模型带入,第Ⅱ层的厚度,第IV层的厚度、外部环境的温度(取80 ℃)、工作的时间(取1 800 s),即

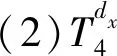
(22)

(23)

(3)第Ⅱ层的厚度不小于0.6 mm,不大于25.0 mm,第IV层的厚度不小于0.6 mm,不大于6.4 mm即

0.6≤dx≤25,0.6≤dy≤6.4

(24)

综上,考虑第Ⅱ、IV层的厚度的合理模型为

(25)

3.2 高温作业专用服材料Ⅱ层IV层厚度参数求解

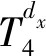
根据模型(25),利用MATLAB软件进行求解得:d2=10.5 mm;d4=5.2 mm。

4 结语

文中讨论了高温作业专用服装的设计问题,通过分析影响温度变化的各个参数,建立了不同材质的一维热传导微分方程模型,然后利用有限差分法对模型进行求解,得到了服装各个层面温度随时间、厚度变化的情况。最后,利用枚举搜索算法求出了在不同温度限制条件下,目标防护效果的最优厚度。但是,在解决问题时,未考虑织物层间的空隙及织物本身的间隙,也未考虑辐射项及双向传热。而解决问题二和三时所使用的枚举算法,时间复杂度高,运算量较大,这也是以后需要改进的地方。