塔形网格上的有理插值

许雨静,赵前进

(安徽理工大学 数学与大数据学院,安徽 淮南 232001)

0 引 言

有理插值是用于解决非线性逼近问题不可或缺的方法.连分式因具有计算简便、运算量少等特性,成为构造有理插值算法的重要工具.近年来,在矩形网格、三角网格上构造混合有理插值用以逼近二元和三元连续函数的算法越来越多[1-7],带有附加条件的切触有理插值[8-9]也很常见.沈晓明等将重心插值与Thiele连分式插值结合,得到了二元Barycentric-Thiele混合有理插值[7].这种插值方法既有重心插值的优点,又有连分式的优点,如通过选择合适的权值,可以避免极点的产生,且计算量小等.文献[10]证实,在特定条件下,连分式插值还具有保水平渐近线的性质.

现有塔型网格上的Thiele型分叉连分式插值算法[11]要定义初始点的值,这给计算过程带来不便.针对这一情况,出现了不同塔型格式的Newton-Thiele型混合有理插值.但数值实验发现,这种算法在x=0处附近的插值效果并不理想.为弥补这一缺陷,本文将构造新的Thiele型分叉连分式算法,并用实例验证其逼近效果要优于Newton-Thiele算法.

给定实数点集X={x0,x1,…,xm}∈[a,b]⊂,以及f(x)∈C1[a,b]是定义在区间上的连续实函数,其中,当xi≠xj时,有f(xi)≠f(xj).

(1)

其中,bk=φ[x0,x1,…,xk],φ[x0,x1,…,xk]称为f(x)的k阶逆差商,其定义为:

φ[xp]=f(xp),

(2)

(3)

(4)

T(x)称为函数f(x)的Thiele型插值函数.

1 连分式有理插值算法

将Thiele型连分式应用于新的塔型网格上,对Thiele型连分式插值进行类似张量积的处理,从而在塔形网格上构造分叉连分式插值,并给出递推算法,以证明该插值的有效性.

(5)

其中,i=0,1,…,n.则有:

(6)

当j、k=0,1,…,2(n-i)时,有:

(7)

(8)

其中,

(9)

(10)

式(5)～(8)为连分式有理插值函数.

下面证明其有效性.

φ[xi,yj,zk]=f(xi,yj,zk),

(11)

(12)

(13)

(14)

(15)

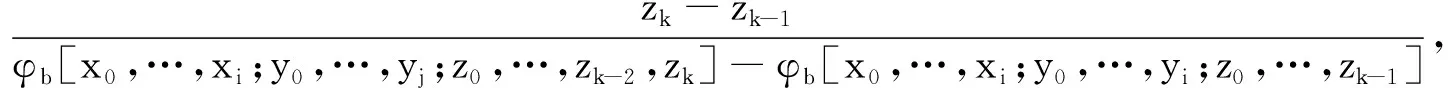
(16)

(17)

(18)

定理1若定义1中的所有混合偏逆差商均存在:

其中,i=0,1,…,n;j、k=0,1,…,2(n-i).则有理插值函数满足:

Rn(xi,yj,zk)=f(xi,yj,zk).

(19)

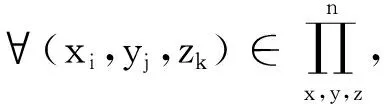
因此,

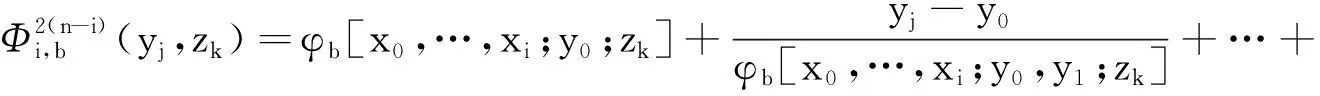
同理可证:

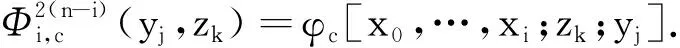
当i=0,1,…,n时,有:

故由式(5)得:

定理1得证.

2 特征定理

引理1对i=0,1,…,n,令

(20)

则

(21)

(22)

证明证明方法同文献[11]的引理4.5,令n=n-1即可.

(23)

degyPn(x,y,z)=degyQn(x,y,z)=2n(n+1)(n+2)/3,

(24)

degzPn(x,y,z)=degzQn(x,y,z)=2n(n+1)(n+2)/3.

(25)

证明式(23)可由Thiele型连分式插值最高次公式[12]得到.

下面证明式(24)和式(25).

当n=1时,

显然成立.

假设当n=k时成立,即

degyPk(x,y,z)=degyQk(x,y,z)=k(k+1)(k+2)/3,
degzPk(x,y,z)=degzQk(x,y,z)=k(k+1)(k+2)/3.

下面证明当n=k+1时,结论也满足:

为证明该定理,不妨记:

其中,τ=k,k+1,…

其中,τ=k-1,k,…

不难看出,

且

因此,可得:

同理可证:

degzPk+1(x,y,z)=degzQk+1(x,y,z)=2(k+1)(k+2)(k+3)/3.

假设成立,该定理得证.

3 误差分析

下面给出连分式有理插值函数的误差估计.

定理3假设函数f(x,y,z)是包含在区间Ω=[a,b]×[c,d]×[e,f]上的三元函数,且混合偏逆差商均存在,则对∀(x,y,z)∈G,存在(θi,δj,i,ζi)∈G,(αi,βi)∈[c,d]×[e,f],使得

(26)

其中,Rn(x,y,z)=Pn(x,y,z)/Qn(x,y,z).

当i=0,1,…,n;j、k=0,1,…,2(n-i)时,有:

(27)

θi∈I[x0,…,xi],δj,i∈I[y0,…,yj],ξi∈I[z0,…,z2(n-i),z],αi∈I[x0,…,xi],βi∈I[y0,…,y2(n-i),y],τ∈I[x0,…,xi,x],且I[x0,…,xi]是包含x0,…,xi的最小区间.

证明令En(x,y,z)=Qn(x,y,z)f(x,y,z)-Pn(x,y,z),(x,y,z)∈G.

En(xi,yj,zk)=0.

因此,基于张量积形式的Newton差商记为En[x0,…,xi;y0,…,yi;z0,…,zk],且En[x0,…,xi;y0,…,yi;z0,…,zk]=0.

利用展开式,可得:

4 数值举例

下面给出塔型网格Newton-Thiele型混合有理插值算法与连分式有理插值算法的数值例子,并对结果进行对比与分析.

不妨记RT(x,y,z)为连分式有理插值函数,RN(x,y,z)为Newton-Thiele型混合有理插值函数,eT(x,y,z)、eN(x,y,z)分别为RT(x,y,z)、RN(x,y,z)与被插值函数的绝对误差,即

eT(x,y,z)=|f(x,y,z)-RT(x,y,z)|;eN(x,y,z)=|f(x,y,z)-RN(x,y,z)|.

例1设函数f(x,y,z)=(x2+y2+z2)e-(x+y+z),且(x,y,z)∈{(xi,yj,zk)|i=0,1;j、k=0,1,…,2(1-i)},不妨令n=2,则给定的插值点见表1和表2.

表1 x0=0 初始表

表2 x1=1初始表

当i=2时,x2=2,y0=1/2,z0=1/3;f(x1,y0,z0)=0.256 5.

由(5)～(18)式,可得:

当i=0,1,2时,有:

当i=0,j、k=0,1,2,3,4时,有:

其中,

同理,当i=1;j、k=0,1,2时,可求bi,j(z),ci,k(y).

当i=2;j、k=0时,有:

通过计算,可得连分式有理插值系数,见表3、表4和表5.

表4 RT(x,y,z)、RN(x,y,z)系数表

表5 RT(x,y,z)插值c1,j(y),b1,j(z)系数表

下面计算Newton-Thiele型混合有理插值系数.

通过计算得,当i=0时,插值系数见表3和表4.

当i=1时,插值系数见表6.

表6 RN(x,y,z)插值c1,j(y),b1,j(z)系数表

当i=2时,插值系数为:

通过大量的实验对比发现,当x的取值趋于0,y,z取定义域内的任意值时,连分式有理插值算法的误差明显小于Newton-Thiele型混合有理插值算法的误差,且插值效果较好,表7仅代表一小部分数据.

图1 x=0.01,y=0.8,z∈[1/3,1]函数图像

图2 x=0.001,y=0.8,z∈[1/3,1]函数图像

5 结 论

Newton插值定义于差商上,而Thiele型连分式定义于逆差商上,这就会导致两者在插值问题上出现不同.文中数值例子证明,在某些点的周围,连分式有理插值要优于Newton-Thiele型混合有理插值.但在整个定义域内,前者与后者的逼近效果不相上下.因此,后续研究的方向应着重放在计算过程,以及若碰到极点的情况该如何处理方面.